2020—2021学年人教版七年级数学下册导学课件 5.1.1 相交线(共18张ppt)
文档属性
| 名称 | 2020—2021学年人教版七年级数学下册导学课件 5.1.1 相交线(共18张ppt) |

|
|
| 格式 | zip | ||
| 文件大小 | 434.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-04-19 00:00:00 | ||
图片预览






文档简介
(共18张PPT)
5.1 相交线
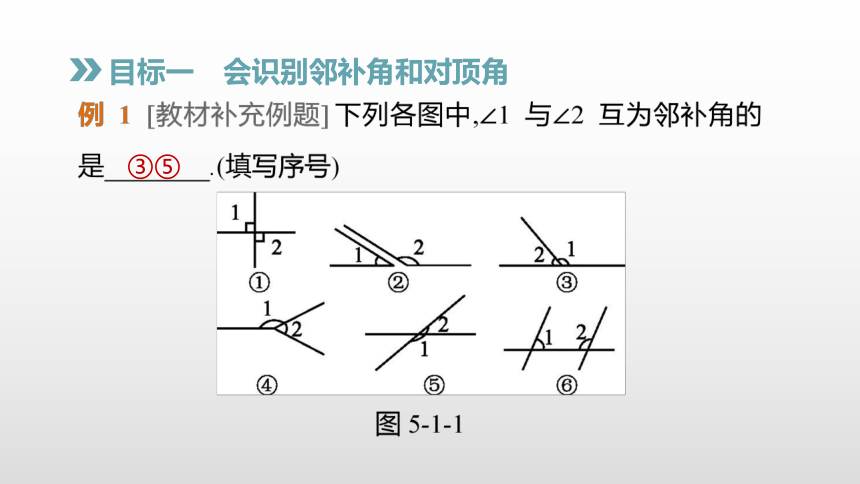
目标一 会识别邻补角和对顶角
③⑤
归纳总结
识别邻补角的方法
邻补角的识别
一看这两个角有没有公共边
二看这两个角的另一边是否互为反向延长线
注意
在两条相交直线中,一个角的邻补角有两个,注意不要遗漏
图5-1-2
解:(1)∠AOD和∠BOC是由直线AB,CD相交形成的对顶角.
(2)∠BOD和∠FOC的对顶角分别是∠AOC和∠DOE.
(3)∠AOF的邻补角是∠AOE和∠BOF.
归纳总结
识别对顶角的方法
对顶角的识别
一看它们有没有公共顶点
二看这两个角的两边是否互为反向延长线
邻补角与对顶角的区别
对顶角无公共边,邻补角有公共边
目标二 会进行与对顶角、邻补角有关的计算与说理
解:由邻补角的定义,得∠BOC=180°-∠AOC=180°-40°=140°.
因为OE平分∠BOC,
解:OE是∠AOC的平分线.
理由:因为OF平分∠BOD(已知),
所以∠BOF=∠DOF(角平分线的定义).
因为∠AOE=∠BOF,∠COE=∠DOF(对顶角相等),
所以∠AOE=∠COE(等量代换),
所以OE是∠AOC的平分线(角平分线的定义).
归纳总结
学习几何需要掌握三种语言:图形语言、文字语言、符号语言,要学会这三种语言之间的相互转化.学习几何说理的注意点:(1)要有条理地说出由已知到结论的过程;(2)每一步由“因为……所以……”组成,且用括号注明推理的根据.
小
结
知识点一 邻补角、对顶角的概念
1.邻补角:若两角有 条公共边,它们的另一边互为 ,具有这种关系的两个角,互为邻补角.?
2.对顶角:若两角有一个公共 ,并且两角的两边互为 ,具有这种位置关系的两个角,互为对顶角.?
一
反向延长线
顶点
反向延长线
图形语言(基本图形)
文字语言
符号语言
邻补角 ,即互为邻补角的两个角之和为 °?
因为∠1与∠2是邻补角,
所以∠1+∠2=180°
(
)?
知识点二 邻补角、对顶角的性质
互补
180
邻补角的性质
图形语言(基本图形)
文字语言
符号语言
对顶角 ?
因为∠BOC和∠AOD是对顶角,
所以∠BOC=∠AOD( )?
相等
对顶角相等
反
思
解:
(1)√
(2)× 理由:对顶角相等,但是相等的角不一定是对顶角,如图①中的∠
1
=∠2,但是∠1与∠2不是对顶角.
(3)√
(4)× 理由:如图②,∠1=45°,∠2=135°.因为∠1+∠2=180°,所以∠1与∠2互补,但它们不是邻补角.
1
2
图①
1
2
图②
5.1 相交线
目标一 会识别邻补角和对顶角
③⑤
归纳总结
识别邻补角的方法
邻补角的识别
一看这两个角有没有公共边
二看这两个角的另一边是否互为反向延长线
注意
在两条相交直线中,一个角的邻补角有两个,注意不要遗漏
图5-1-2
解:(1)∠AOD和∠BOC是由直线AB,CD相交形成的对顶角.
(2)∠BOD和∠FOC的对顶角分别是∠AOC和∠DOE.
(3)∠AOF的邻补角是∠AOE和∠BOF.
归纳总结
识别对顶角的方法
对顶角的识别
一看它们有没有公共顶点
二看这两个角的两边是否互为反向延长线
邻补角与对顶角的区别
对顶角无公共边,邻补角有公共边
目标二 会进行与对顶角、邻补角有关的计算与说理
解:由邻补角的定义,得∠BOC=180°-∠AOC=180°-40°=140°.
因为OE平分∠BOC,
解:OE是∠AOC的平分线.
理由:因为OF平分∠BOD(已知),
所以∠BOF=∠DOF(角平分线的定义).
因为∠AOE=∠BOF,∠COE=∠DOF(对顶角相等),
所以∠AOE=∠COE(等量代换),
所以OE是∠AOC的平分线(角平分线的定义).
归纳总结
学习几何需要掌握三种语言:图形语言、文字语言、符号语言,要学会这三种语言之间的相互转化.学习几何说理的注意点:(1)要有条理地说出由已知到结论的过程;(2)每一步由“因为……所以……”组成,且用括号注明推理的根据.
小
结
知识点一 邻补角、对顶角的概念
1.邻补角:若两角有 条公共边,它们的另一边互为 ,具有这种关系的两个角,互为邻补角.?
2.对顶角:若两角有一个公共 ,并且两角的两边互为 ,具有这种位置关系的两个角,互为对顶角.?
一
反向延长线
顶点
反向延长线
图形语言(基本图形)
文字语言
符号语言
邻补角 ,即互为邻补角的两个角之和为 °?
因为∠1与∠2是邻补角,
所以∠1+∠2=180°
(
)?
知识点二 邻补角、对顶角的性质
互补
180
邻补角的性质
图形语言(基本图形)
文字语言
符号语言
对顶角 ?
因为∠BOC和∠AOD是对顶角,
所以∠BOC=∠AOD( )?
相等
对顶角相等
反
思
解:
(1)√
(2)× 理由:对顶角相等,但是相等的角不一定是对顶角,如图①中的∠
1
=∠2,但是∠1与∠2不是对顶角.
(3)√
(4)× 理由:如图②,∠1=45°,∠2=135°.因为∠1+∠2=180°,所以∠1与∠2互补,但它们不是邻补角.
1
2
图①
1
2
图②
