青岛版八年级下册第9章 解直角三角形全章学案
文档属性
| 名称 | 青岛版八年级下册第9章 解直角三角形全章学案 |

|
|
| 格式 | zip | ||
| 文件大小 | 79.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2012-02-26 00:00:00 | ||
图片预览




文档简介
9.1锐角三角比
【教师寄语】:收获只属于勇于探索的人
【学习目标】:1、通过实例明确并认识锐角三角比的概念;
2、正确理解三角比符号的含义,掌握锐角三角比的表示;
3、学会根据定义求锐角的三角比;
【重点】:会根据定义求锐角的三角比
【难点】:正弦、余弦、正切概念的建立及表示
【学习过程】:
一、快乐预习:
1、如图,在Rt△ABC中,指出斜边是
∠A的对边是 邻边是
∠B的对边是 邻边是
2、自主学习课本62页“观察与思考”,认真完成(1)(2)(3)中的每一个问题。思考:如果继续在图9-1中的AB(或AB的延长线上)选出其它的点,结论会怎样?
3、结论:当锐角A的大小确定后,不论以∠A为内角的直角三角形的大小(边长)如何变化,∠A的对边与斜边的比值______ ___。
4、总结定义:
sinA= cosA= tanA=
锐角A的正弦、余弦、正切统称锐角A的___ ____ (也叫锐角A的 ) 。
5、如上图,在Rt△ABC中,∠C=900, AC=4,BC=2,求∠A的正弦,余弦,正切的值
二、合作探究:
1、思考:如果Rt△ABC∽Rt△A′B′C′,∠C=∠C′=900 ,sinA等于sinA′吗?为什么?cosA与cosA′呢?
2、变式训练:(1)在Rt⊿ABC中,∠C=900,BC=2,sinA=,则边AB的长为 。
(2)若∠A为锐角,sinA=,则cosA= 。
三、拓展提高:
Rt△ABC中,∠C=90 ,三边分别为a、b、c根据正余弦的定义,并结合勾股定理探索下列问题:
①cosA与sinB什么关系?
②sin2 A与cos2A什么关系
③sin40 =cosa, ∠ a=________度
④tanA·tanB=_____
⑤tanA与什么关系?
4、系统总结:
四、感恩达标
1、 如图,在Rt△ABC中,∠C=900, AB=3,BC=2,求∠A的正弦,余弦,正切的值?
2、在△ABC中,∠B=900,AB=4,BC=3,则sinA= ;
3、在Rt△ABC中,∠C=900,∠A、∠B、∠C的对边分别a、b、c,若a=3b,求∠B的正弦、余弦、正切的值。
4、 △ABC中,AC=3,BC=4,AB=5,则tanB=_____。
5、在Rt△ABC中,∠C=900,AB=8,cosA=,则AC= ,BC= 。
9.2 30°,45°,60°角的三角比
【教师寄语】:数学来源于生活,并应用于生活。
【学习目标】:1、记住300、450、600角的三角比,能够用它进行计算。
2、能够根据300、450、600的三角比的值,求出相应锐角的大小。
3、能够运用300、450、600角的三角比解决有关问题。
【重点】:熟练识记30°,45°,60°角的三角比值,并能用它们进行简单的计算。
【难点】:明确这些特殊角的三角比值的探求方法。
【学习过程】:
一、快乐预习:
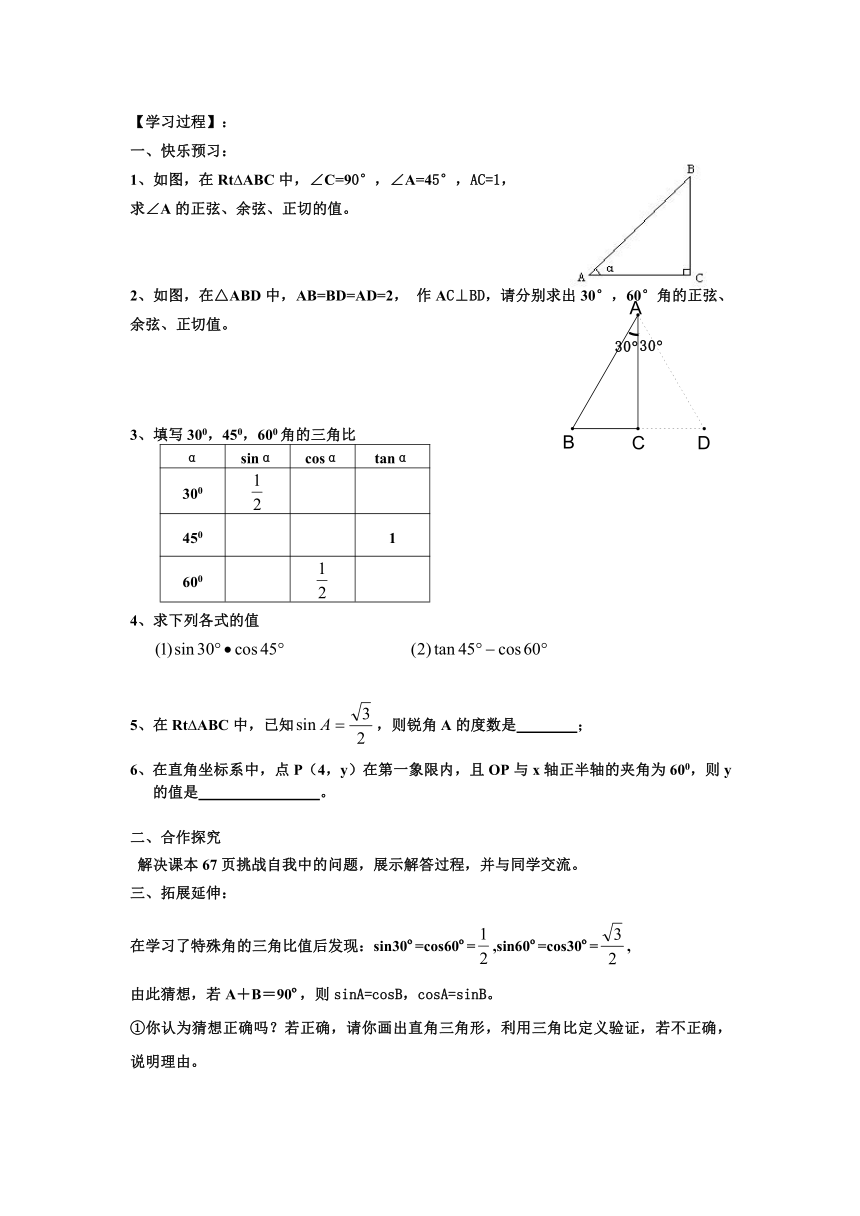
1、如图,在Rt ABC中,∠C=90°,∠A=45°,AC=1,
求∠A的正弦、余弦、正切的值。
2、如图,在△ABD中,AB=BD=AD=2, 作AC⊥BD,请分别求出30°,60°角的正弦、余弦、正切值。
3、填写300,450,600角的三角比
α sinα cosα tanα
300
450 1
600
4、求下列各式的值
5、在Rt ABC中,已知,则锐角A的度数是 ;
6、在直角坐标系中,点P(4,y)在第一象限内,且OP与x轴正半轴的夹角为600,则y的值是 。
二、合作探究
解决课本67页挑战自我中的问题,展示解答过程,并与同学交流。
三、拓展延伸:
在学习了特殊角的三角比值后发现:sin30 =cos60 =,sin60 =cos30 =,
由此猜想,若A+B=90 ,则sinA=cosB,cosA=sinB。
①你认为猜想正确吗?若正确,请你画出直角三角形,利用三角比定义验证,若不正确,说明理由。
②计算tan30 ·tan60 =__________。由此可知,若A+B=90 ,则tanA·tanB=______。
③试一下,写出下列结果:若sin16 =0.2756,则cos74 =______;
若cos42 =0.7431,则sin48 =_____________;
tan31 ·tan59 =______________。
四、感恩达标
1、求下列各式的值
(4)cos300×tan300+tan450×sin600
2、某商场有一自动扶梯,其倾斜角为,高为7m,扶梯长度为多少?
9.3用计算器求锐角三角比
【教师寄语】:数学就在我们身边,要善于发现它。
【学习目标】:1、了解科学计算器有关计算三角比的按键设置及操作方法。
2、能够用计算器进行有关三角比值的计算。
3、会运用计算器辅助解含三角比值计算的实际问题。
【重点】:会用计算器求锐角三角比的值
【难点】:会用计算器进行锐角三角比的四则运算
【学习过程】:
一、快乐预习:
(一)由已知锐角求它的三角比值
1、阅读课本68—70页内容,尝试用计算器求锐角三角比的值,完成70页练习题。
2、想一想,用计算器求锐角三角比的值应该注意什么?总结按键顺序。
3、填写课本70页“观察与思考”中的表格,并完成以下问题:
(1)当锐角α逐渐增大时,它的正弦值 ,余弦值
(2)____<sinα<____,____<cosα<____
(二)由三角比值求相应的锐角
1、阅读课本71—72页内容,尝试用计算器由三角比的值求相应的锐角,完成72页练习题。
2、议一议,由三角比的值求相应的锐角按键顺序与已知锐角求它的三角比值按键顺序有什么不同?
二、合作探究
1、用计算器求下列锐角三角比的值:
= = = =
2、用计算器求下列锐角三角比的值:
3、根据下列三角比的值,用计算器求相应的锐角:
4、利用计算器求下列各式的值:
5、一个人从山底爬到山顶,需先爬的山坡300m,再爬的山坡100m,求山高?(结果精确到0.1m)
三、拓展提高:
分别求出锐角10、100、200、300、400、450、500、600、700、800、890的三角比的值,观察结果,并思考以下问题:
(1)当锐角逐渐增大时,它的正弦和余弦的值分别发生怎样的变化?
(2)你能估计出锐角的正弦值的范围吗? 锐角的余弦值的范围呢?
四、感恩达标
1、用计算器求下列各式的值
(3)已知则
(4)已知则
9.4解直角三角形(一)
【教师寄语】:方法是解决问题的手段,掌握一种好的方法会让你受益无穷。
【学习目标】:1、知道直角三角形中五个元素的关系和解直角三角形的概念。
2、会运用勾股定理、直角三角形的两个锐角互余及锐角三角比解直角三角形。
3、通过解直角三角形的学习,培养分析问题,解决问题的能力,渗透数形结合的思想。
【重点】:解直角三角形的方法
【难点】:三角比在解直角三角形中的灵活运用。
【学习过程】:
一、快乐预习:
1、在Rt ABC中共有几个边元素?几个角元素?请分别写出来。
2、如图,在Rt ABC中,∠C=,a,b,c,∠A,∠B五个元素之间有哪些等量关系呢?
(1)角之间的关系:
(2)边之间的关系:
(3)角与边之间的关系:
3、在Rt△ABC中,∠C=。
已知∠A,∠B,能求出其它的三个量a,b,c吗?
已知两条边的长,能求出其它的三个量吗?
已知一角和一边,能求出其它的三个量吗? 你有什么发现?
二、合作探究:
(1)在Rt ABC中,已知∠C=,a=17.5,c=62.5。解这个直角三角形。
(2)在Rt ABC中,已知∠C=,c=128,∠B=。解这个直角三角形(边长精确到0.01)。
三、拓展提高:
1、你能概括出什么是解直角三角形吗?解直角三角形时,为什么两个已知元素中至少有一条边?
2、直角三角形的解法可以归纳为哪几种情况。
3、在Rt ABC中,已知∠C=。
(1)已知c=15,∠B=,求a; (2)已知∠A=,a =24,求b,c。
4、如图,已知Rt⊿ABC中,斜边BC上的高AD=4,cosB=,则AC=
5、如图,⊿ABC中,∠C=900,∠B=300,AD是⊿ABC的角平分线,若AC=,求线段AD的长。
四、感恩达标:
1、已知在Rt△ABC中,∠C=900,a,b,c,分别为∠A,∠B,∠C所对的边,由下列条件解直角三角形。
(1)已知a=6,b=6,求c, (2)已知a=20,c=20,求∠B;
(3)已知c=30,∠A,600,求a;
2、已知Rt△ABC中,∠C=900,∠A=300,斜边上的高为1,则△ABC三边的长分别为( )
A a=2 ,b=2, c=4, B a=, b=2, c =
C a=,b=2,c=, D a=2, b= , c=
3、在Rt ABC中,已知∠C=,AC=7,∠A=2∠B,求AB,BC的长。
9.4解直角三角形(二)
【教师寄语】:不怕做不到,就怕想不到。
【学习目标】: 1.会把一些非直角三角形的图形转化成直角三角形,从而灵活利用解直角三角形的有关知识解决几何问题。
2. 经历探索通过做辅助线构造直角三角形的转化过程,体会转化的数学思想。
【重难点】:准确做辅助线并选择适当的关系解直角三角形。
【学习过程】:
一、快乐预习:
1、解直角三角形的依据:
(1)三边之间的关系:
(2)锐角之间的关系:
(3)边角之间的关系:
这三个关系中,每个关系式中都包括____元素,知道其中____元素,就可以求出____________。
2、解直角三角形的两种情况。
(1)已知 ,求第三边及两锐角。
(2)已知 和一个 ,求其它两边及另一锐角。
3、思考:若△ABC不是直角三角形,怎么办?如下图,在△ABC中,已知∠A=60 , ∠B=45 ,AC=20厘米,求AB的长。
二、合作探究
1、把非直角△ABC通过做辅助线构造成直角三角时,以不破坏特殊角为标准。
如:在△ABC中,已知AB=1,AC=,∠ABC=450,求BC长
2、如图,在Rt△ABC中,∠A=900,AD⊥BC,垂足为D,∠B=600,AD=3,求BC的长。
三、拓展提高:
1、在等腰三角形中,AB=AC,且一腰长与底边的比为5:8,求sinB,cosB的值。
2、如图,在△ABC中,∠ACB=118°,BC=4,求BC边上的高。
3、 已知如图,在△ABC中,AB=20,AC=30,∠A=1500,求△ABC的面积
四、感恩达标:
1、已知正方形的边长是2cm,对角线的长为:__________________
2、在锐角三角形ABC中,∠C=450,AC=,AB=2,求这个三角形的未知的边和未知的角?
3、在△ABC中,∠B=450,cosC=,AC=5a,则△ABC的面积用含a的式子表示 是
9.5解直角三角形的应用(一)
【教师寄语】:学以致用,在实际应用中体会学数学的乐趣。
【学习目标】:1、知道仰角、俯角的概念,并能将之灵活应用于实际生活。
2、能从实际问题中抽象出几何模型,并能借助计算器解决问题。
3、运用三角比的有关知识来解决有关仰角、俯角的问题。
【重点】:运用三角比的有关知识来解决有关仰角、俯角的问题。
【难点】:从实际问题中抽象出恰当的几何模型,用三角比的有关知识来解决。
【学习过程】:
一、快乐预习:
1、问题感知,解决课本76页问题,请写在下面。
2、读一读课本76页小资料:在实际测量中,从低处观测高处的目标时,_________与_________所成的锐角叫做_________,从高处观测低处的目标时,_______与________所成的锐角叫做______。
3、学习例题,尝试完成课本78页练习1、2。
二、合作探究:
1、小组讨论解决课本例习题,展示解答过程,并与同学交流。
2、反思归纳:把实际问题转化为解直角三角形问题,关键是找出实际问题中的_____________
三、拓展提高:
1、某商场准备改善原有楼梯的安全性能把倾角由40 减至35 ,已知原楼梯长4m,调整后的楼梯会加长多少?楼梯多占多长一段地面?(结果精确到0.01m)
2、一灯柱AB被一钢缆CD固定,CD与地面成40 夹角,且DB=5m,在C点上方2m处加固另一条钢缆ED,那么钢缆ED的长度为多少?(结果精确到0、01m)
四、感恩达标:
1 如图从地面上C、D两处望山顶A,仰角分别是300和500,若从山顶A看地面上的D处时,则( )
A 仰角是450 B俯角是300 C 俯角是600 D俯角是750
2、如上右图某厂房屋顶成人字架形(等腰三角形),如图所示,已知AC=BC=8米,∠A=300,CD⊥AB于点D.
求∠ACB的大小; (2)求AB的长度。
B
C
A
B
C
A
a
b
c
B
C
A
A
B
C
b
c
a
A
C
B
D
A
C
B
A
B
C
视线
水平线
视线
铅
垂
线
仰角
俯角
300
500
【教师寄语】:收获只属于勇于探索的人
【学习目标】:1、通过实例明确并认识锐角三角比的概念;
2、正确理解三角比符号的含义,掌握锐角三角比的表示;
3、学会根据定义求锐角的三角比;
【重点】:会根据定义求锐角的三角比
【难点】:正弦、余弦、正切概念的建立及表示
【学习过程】:
一、快乐预习:
1、如图,在Rt△ABC中,指出斜边是
∠A的对边是 邻边是
∠B的对边是 邻边是
2、自主学习课本62页“观察与思考”,认真完成(1)(2)(3)中的每一个问题。思考:如果继续在图9-1中的AB(或AB的延长线上)选出其它的点,结论会怎样?
3、结论:当锐角A的大小确定后,不论以∠A为内角的直角三角形的大小(边长)如何变化,∠A的对边与斜边的比值______ ___。
4、总结定义:
sinA= cosA= tanA=
锐角A的正弦、余弦、正切统称锐角A的___ ____ (也叫锐角A的 ) 。
5、如上图,在Rt△ABC中,∠C=900, AC=4,BC=2,求∠A的正弦,余弦,正切的值
二、合作探究:
1、思考:如果Rt△ABC∽Rt△A′B′C′,∠C=∠C′=900 ,sinA等于sinA′吗?为什么?cosA与cosA′呢?
2、变式训练:(1)在Rt⊿ABC中,∠C=900,BC=2,sinA=,则边AB的长为 。
(2)若∠A为锐角,sinA=,则cosA= 。
三、拓展提高:
Rt△ABC中,∠C=90 ,三边分别为a、b、c根据正余弦的定义,并结合勾股定理探索下列问题:
①cosA与sinB什么关系?
②sin2 A与cos2A什么关系
③sin40 =cosa, ∠ a=________度
④tanA·tanB=_____
⑤tanA与什么关系?
4、系统总结:
四、感恩达标
1、 如图,在Rt△ABC中,∠C=900, AB=3,BC=2,求∠A的正弦,余弦,正切的值?
2、在△ABC中,∠B=900,AB=4,BC=3,则sinA= ;
3、在Rt△ABC中,∠C=900,∠A、∠B、∠C的对边分别a、b、c,若a=3b,求∠B的正弦、余弦、正切的值。
4、 △ABC中,AC=3,BC=4,AB=5,则tanB=_____。
5、在Rt△ABC中,∠C=900,AB=8,cosA=,则AC= ,BC= 。
9.2 30°,45°,60°角的三角比
【教师寄语】:数学来源于生活,并应用于生活。
【学习目标】:1、记住300、450、600角的三角比,能够用它进行计算。
2、能够根据300、450、600的三角比的值,求出相应锐角的大小。
3、能够运用300、450、600角的三角比解决有关问题。
【重点】:熟练识记30°,45°,60°角的三角比值,并能用它们进行简单的计算。
【难点】:明确这些特殊角的三角比值的探求方法。
【学习过程】:
一、快乐预习:
1、如图,在Rt ABC中,∠C=90°,∠A=45°,AC=1,
求∠A的正弦、余弦、正切的值。
2、如图,在△ABD中,AB=BD=AD=2, 作AC⊥BD,请分别求出30°,60°角的正弦、余弦、正切值。
3、填写300,450,600角的三角比
α sinα cosα tanα
300
450 1
600
4、求下列各式的值
5、在Rt ABC中,已知,则锐角A的度数是 ;
6、在直角坐标系中,点P(4,y)在第一象限内,且OP与x轴正半轴的夹角为600,则y的值是 。
二、合作探究
解决课本67页挑战自我中的问题,展示解答过程,并与同学交流。
三、拓展延伸:
在学习了特殊角的三角比值后发现:sin30 =cos60 =,sin60 =cos30 =,
由此猜想,若A+B=90 ,则sinA=cosB,cosA=sinB。
①你认为猜想正确吗?若正确,请你画出直角三角形,利用三角比定义验证,若不正确,说明理由。
②计算tan30 ·tan60 =__________。由此可知,若A+B=90 ,则tanA·tanB=______。
③试一下,写出下列结果:若sin16 =0.2756,则cos74 =______;
若cos42 =0.7431,则sin48 =_____________;
tan31 ·tan59 =______________。
四、感恩达标
1、求下列各式的值
(4)cos300×tan300+tan450×sin600
2、某商场有一自动扶梯,其倾斜角为,高为7m,扶梯长度为多少?
9.3用计算器求锐角三角比
【教师寄语】:数学就在我们身边,要善于发现它。
【学习目标】:1、了解科学计算器有关计算三角比的按键设置及操作方法。
2、能够用计算器进行有关三角比值的计算。
3、会运用计算器辅助解含三角比值计算的实际问题。
【重点】:会用计算器求锐角三角比的值
【难点】:会用计算器进行锐角三角比的四则运算
【学习过程】:
一、快乐预习:
(一)由已知锐角求它的三角比值
1、阅读课本68—70页内容,尝试用计算器求锐角三角比的值,完成70页练习题。
2、想一想,用计算器求锐角三角比的值应该注意什么?总结按键顺序。
3、填写课本70页“观察与思考”中的表格,并完成以下问题:
(1)当锐角α逐渐增大时,它的正弦值 ,余弦值
(2)____<sinα<____,____<cosα<____
(二)由三角比值求相应的锐角
1、阅读课本71—72页内容,尝试用计算器由三角比的值求相应的锐角,完成72页练习题。
2、议一议,由三角比的值求相应的锐角按键顺序与已知锐角求它的三角比值按键顺序有什么不同?
二、合作探究
1、用计算器求下列锐角三角比的值:
= = = =
2、用计算器求下列锐角三角比的值:
3、根据下列三角比的值,用计算器求相应的锐角:
4、利用计算器求下列各式的值:
5、一个人从山底爬到山顶,需先爬的山坡300m,再爬的山坡100m,求山高?(结果精确到0.1m)
三、拓展提高:
分别求出锐角10、100、200、300、400、450、500、600、700、800、890的三角比的值,观察结果,并思考以下问题:
(1)当锐角逐渐增大时,它的正弦和余弦的值分别发生怎样的变化?
(2)你能估计出锐角的正弦值的范围吗? 锐角的余弦值的范围呢?
四、感恩达标
1、用计算器求下列各式的值
(3)已知则
(4)已知则
9.4解直角三角形(一)
【教师寄语】:方法是解决问题的手段,掌握一种好的方法会让你受益无穷。
【学习目标】:1、知道直角三角形中五个元素的关系和解直角三角形的概念。
2、会运用勾股定理、直角三角形的两个锐角互余及锐角三角比解直角三角形。
3、通过解直角三角形的学习,培养分析问题,解决问题的能力,渗透数形结合的思想。
【重点】:解直角三角形的方法
【难点】:三角比在解直角三角形中的灵活运用。
【学习过程】:
一、快乐预习:
1、在Rt ABC中共有几个边元素?几个角元素?请分别写出来。
2、如图,在Rt ABC中,∠C=,a,b,c,∠A,∠B五个元素之间有哪些等量关系呢?
(1)角之间的关系:
(2)边之间的关系:
(3)角与边之间的关系:
3、在Rt△ABC中,∠C=。
已知∠A,∠B,能求出其它的三个量a,b,c吗?
已知两条边的长,能求出其它的三个量吗?
已知一角和一边,能求出其它的三个量吗? 你有什么发现?
二、合作探究:
(1)在Rt ABC中,已知∠C=,a=17.5,c=62.5。解这个直角三角形。
(2)在Rt ABC中,已知∠C=,c=128,∠B=。解这个直角三角形(边长精确到0.01)。
三、拓展提高:
1、你能概括出什么是解直角三角形吗?解直角三角形时,为什么两个已知元素中至少有一条边?
2、直角三角形的解法可以归纳为哪几种情况。
3、在Rt ABC中,已知∠C=。
(1)已知c=15,∠B=,求a; (2)已知∠A=,a =24,求b,c。
4、如图,已知Rt⊿ABC中,斜边BC上的高AD=4,cosB=,则AC=
5、如图,⊿ABC中,∠C=900,∠B=300,AD是⊿ABC的角平分线,若AC=,求线段AD的长。
四、感恩达标:
1、已知在Rt△ABC中,∠C=900,a,b,c,分别为∠A,∠B,∠C所对的边,由下列条件解直角三角形。
(1)已知a=6,b=6,求c, (2)已知a=20,c=20,求∠B;
(3)已知c=30,∠A,600,求a;
2、已知Rt△ABC中,∠C=900,∠A=300,斜边上的高为1,则△ABC三边的长分别为( )
A a=2 ,b=2, c=4, B a=, b=2, c =
C a=,b=2,c=, D a=2, b= , c=
3、在Rt ABC中,已知∠C=,AC=7,∠A=2∠B,求AB,BC的长。
9.4解直角三角形(二)
【教师寄语】:不怕做不到,就怕想不到。
【学习目标】: 1.会把一些非直角三角形的图形转化成直角三角形,从而灵活利用解直角三角形的有关知识解决几何问题。
2. 经历探索通过做辅助线构造直角三角形的转化过程,体会转化的数学思想。
【重难点】:准确做辅助线并选择适当的关系解直角三角形。
【学习过程】:
一、快乐预习:
1、解直角三角形的依据:
(1)三边之间的关系:
(2)锐角之间的关系:
(3)边角之间的关系:
这三个关系中,每个关系式中都包括____元素,知道其中____元素,就可以求出____________。
2、解直角三角形的两种情况。
(1)已知 ,求第三边及两锐角。
(2)已知 和一个 ,求其它两边及另一锐角。
3、思考:若△ABC不是直角三角形,怎么办?如下图,在△ABC中,已知∠A=60 , ∠B=45 ,AC=20厘米,求AB的长。
二、合作探究
1、把非直角△ABC通过做辅助线构造成直角三角时,以不破坏特殊角为标准。
如:在△ABC中,已知AB=1,AC=,∠ABC=450,求BC长
2、如图,在Rt△ABC中,∠A=900,AD⊥BC,垂足为D,∠B=600,AD=3,求BC的长。
三、拓展提高:
1、在等腰三角形中,AB=AC,且一腰长与底边的比为5:8,求sinB,cosB的值。
2、如图,在△ABC中,∠ACB=118°,BC=4,求BC边上的高。
3、 已知如图,在△ABC中,AB=20,AC=30,∠A=1500,求△ABC的面积
四、感恩达标:
1、已知正方形的边长是2cm,对角线的长为:__________________
2、在锐角三角形ABC中,∠C=450,AC=,AB=2,求这个三角形的未知的边和未知的角?
3、在△ABC中,∠B=450,cosC=,AC=5a,则△ABC的面积用含a的式子表示 是
9.5解直角三角形的应用(一)
【教师寄语】:学以致用,在实际应用中体会学数学的乐趣。
【学习目标】:1、知道仰角、俯角的概念,并能将之灵活应用于实际生活。
2、能从实际问题中抽象出几何模型,并能借助计算器解决问题。
3、运用三角比的有关知识来解决有关仰角、俯角的问题。
【重点】:运用三角比的有关知识来解决有关仰角、俯角的问题。
【难点】:从实际问题中抽象出恰当的几何模型,用三角比的有关知识来解决。
【学习过程】:
一、快乐预习:
1、问题感知,解决课本76页问题,请写在下面。
2、读一读课本76页小资料:在实际测量中,从低处观测高处的目标时,_________与_________所成的锐角叫做_________,从高处观测低处的目标时,_______与________所成的锐角叫做______。
3、学习例题,尝试完成课本78页练习1、2。
二、合作探究:
1、小组讨论解决课本例习题,展示解答过程,并与同学交流。
2、反思归纳:把实际问题转化为解直角三角形问题,关键是找出实际问题中的_____________
三、拓展提高:
1、某商场准备改善原有楼梯的安全性能把倾角由40 减至35 ,已知原楼梯长4m,调整后的楼梯会加长多少?楼梯多占多长一段地面?(结果精确到0.01m)
2、一灯柱AB被一钢缆CD固定,CD与地面成40 夹角,且DB=5m,在C点上方2m处加固另一条钢缆ED,那么钢缆ED的长度为多少?(结果精确到0、01m)
四、感恩达标:
1 如图从地面上C、D两处望山顶A,仰角分别是300和500,若从山顶A看地面上的D处时,则( )
A 仰角是450 B俯角是300 C 俯角是600 D俯角是750
2、如上右图某厂房屋顶成人字架形(等腰三角形),如图所示,已知AC=BC=8米,∠A=300,CD⊥AB于点D.
求∠ACB的大小; (2)求AB的长度。
B
C
A
B
C
A
a
b
c
B
C
A
A
B
C
b
c
a
A
C
B
D
A
C
B
A
B
C
视线
水平线
视线
铅
垂
线
仰角
俯角
300
500
同课章节目录
- 第1章 图形的相似
- 1.1 相似多边形
- 1.2 怎样判定三角形相似
- 1.3 相似三角形的性质
- 1.4 图形的位似
- 第2章 解直角三角形
- 2.1 锐角三角比
- 2.2 30°,45°,60°角的三角比
- 2.3 用计算器求锐角三角比
- 2.4 解直角三角形
- 2.5 解直角三角形的应用
- 第3章 对圆的进一步认识
- 3.1 圆的对称性
- 3.2 确定圆的条件
- 3.3 圆周角
- 3.4 直线与圆的位置关系
- 3.5 三角形的内切圆
- 3.6 弧长及扇形面积的计算
- 3.7 正多边形与圆
- 课题学习 图形变换与图案设计
- 第4章 一元二次方程
- 4.1 一元二次方程
- 4.2 用配方法解一元二次方程
- 4.3 用公式法解一元二次方程
- 4.4 用因式分解法解一元二次方程
- 4.5 一元二次方程的应用
- 4.6 一元二次方程根与系数的关系
