2020-2021学年人教版数学八年级(下册)18.1.2平行四边形的判定-课件(共17张ppt)
文档属性
| 名称 | 2020-2021学年人教版数学八年级(下册)18.1.2平行四边形的判定-课件(共17张ppt) |

|
|
| 格式 | zip | ||
| 文件大小 | 667.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-04-19 11:12:48 | ||
图片预览


文档简介
(共17张PPT)
课题:平行四边形的判定
人教版八年级数学下册
第十八章
难点名称:探究并掌握平行四边形的几种判定方法,并能根据平行四边形的判定方法进行合情推理。
目录
CONTENTS
2
B
如图,
取两根等长木条AB、CD,将他们平行放置,再用两根木条BC、AD加固,得到的四边形ABCD是一个平行四边形,想一想这是为什么?
大家齐动手
导入
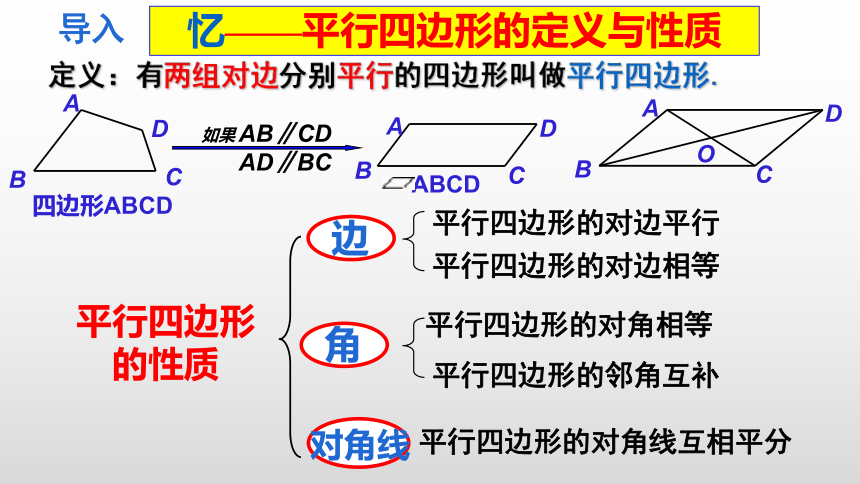
定义:有两组对边分别平行的四边形叫做平行四边形.
A
B
C
D
四边形ABCD
如果
AB∥CD
AD∥BC
B
D
ABCD
A
C
B
D
A
C
O
平行四边形的性质
边
平行四边形的对边平行
平行四边形的对边相等
角
平行四边形的对角相等
平行四边形的邻角互补
对角线
平行四边形的对角线互相平分
忆——平行四边形的定义与性质
导入
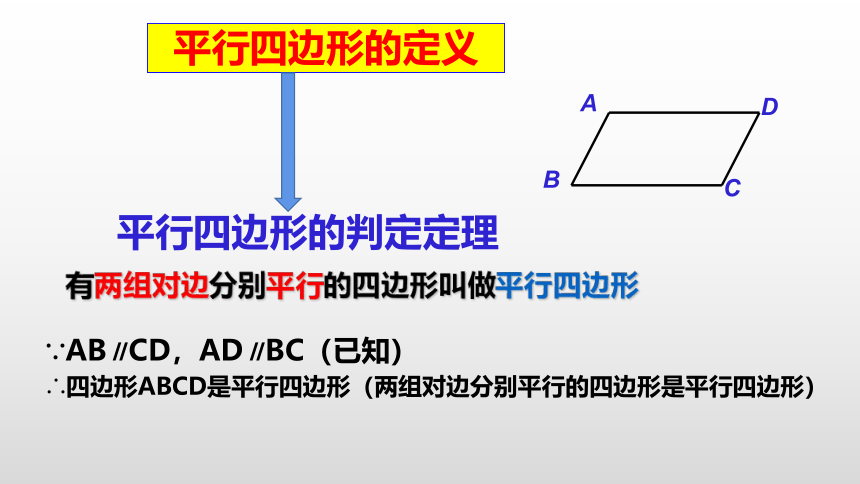
有两组对边分别平行的四边形叫做平行四边形
B
D
A
C
平行四边形的定义
平行四边形的判定定理
∵AB∥CD,AD∥BC(已知)
∴四边形ABCD是平行四边形(两组对边分别平行的四边形是平行四边形)
你能说出下列平行四边形性质的逆命题吗?
①两组对边分别平行的四边形是平行四边形(定义).
②两组对边分别相等的四边形是平行四边形.
③两组对角分别相等的四边形是平行四边形.
④对角线互相平分的四边形是平行四边形.
学
习
新
知
追问:你能根据平行四边形的定义证明这些命题的正确性吗?
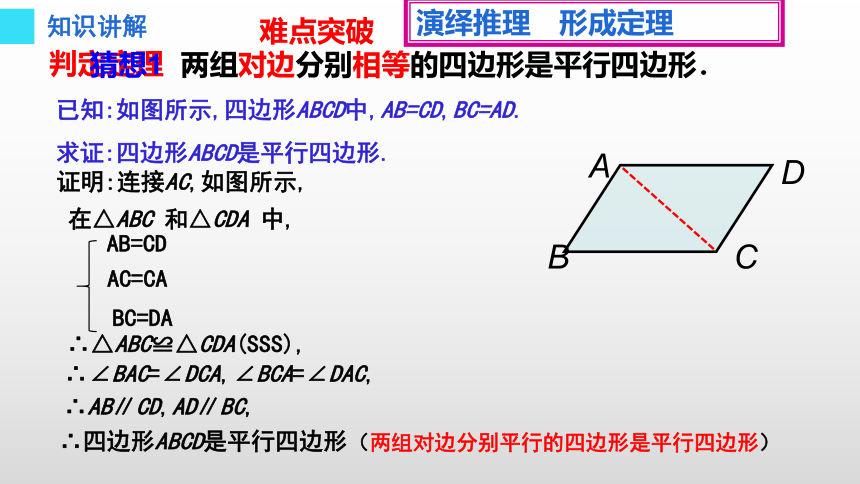
已知:如图所示,四边形ABCD中,AB=CD,BC=AD.
求证:四边形ABCD是平行四边形.
在△ABC
和△CDA
中,
A
B
C
D
两组对边分别相等的四边形是平行四边形.
判定定理
猜想1
演绎推理 形成定理
知识讲解
难点突破
证明:连接AC,如图所示,
∴四边形ABCD是平行四边形
∴△ABC≌△CDA(SSS),
∴∠BAC=∠DCA,∠BCA=∠DAC,
∴AB∥CD,AD∥BC,
AB=CD
AC=CA
BC=DA
(两组对边分别平行的四边形是平行四边形)
B
如图,
取两根等长木条AB、CD,将他们平行放置,在用两根木条BC、AD加固,得到的四边形ABCD是一个平行四边形,想一想这是为什么?
大家齐动手
证明:∵ 多边形ABCD是四边形,
∴ ∠A+∠B+∠C+∠D=360°.
如图,在四边形ABCD中,∠A=∠C,∠B=∠D.
求证:四边形ABCD是平行四边形.
演绎推理 形成定理
两组对角分别相等的四边形是平行四边形.
判定定理
猜想2
D
A
B
C
知识讲解
难点突破
又∵ ∠A=∠C,∠B=∠D,
∴ ∠A+∠B=180°,
∠B+∠C=180°.
∴ AD∥BC,AB∥DC.
∴ 四边形ABCD是平行四边形
(两组对边分别平行的四边形是平行四边形)
已知:如图所示,四边形ABCD中,对角线AC与BD交于点O,且OA=OC,OB=OD.求证:四边形ABCD是平行四边形.
对角线互相平分的四边形是平行四边形
证明:在△AOB和△COD中,
B
D
A
C
O
判定定理
难点突破
知识讲解
猜想3
∴△AOB
≌△COD(SAS),
∴四边形ABCD是平行四边形(两组对边分别平行的四边形是平行四边形)
∴AB∥CD
AO=CO
∠AOB=∠COD
BO=DO
∴∠ABO=∠CDO
同理可证AD∥BC
平行四边形的判定
A
B
C
D
1.两组对边分别平行的四边形是平行四边形。
2.两组对边分别相等的四边形是平行四边形。
∵AB=CD,AD=BC(已知)
∴四边形ABCD是平行四边形(两组对边分别相等的四边形是平行四边形)
4.
对角线互相平分的四边形是平行四边形。
∵OA=OC,OB=OD(已知)
∴四边形ABCD是平行四边形(对角线互相平分的四边形是平行四边形)
3.两组对角分别相等的四边形是平行四边形。
∴四边形ABCD是平行四边形(两组对角分别相等的四边形是平行四边形)
∵∠A=∠C,∠B=∠D(已知)
0
A
B
C
D
根据图形,添加一个条件使四边形ABCD是平行四边形.
1.
∵AB=CD
,
.
∴四边形ABCD是平行四边形
2.∵AB//CD
,
.
∴四边形ABCD是平行四边形
3.∵∠A=∠C
,
.
∴四边形ABCD是平行四边形
A
B
C
D
o
4.根据右图填空:
∵四边形对角线AC、BD交于点O.
,
OC=OA
∴四边形ABCD是
.
AD=BC
AD∥BC
∠B=∠C
OD=OB
平行四边形
课堂练习
如图18.1-11,□ABCD的对角线AC、BD相交于点O,E,F是AC上的两点,并且AE=CF。
求证:四边形BFDE是平行四边形。
证明:
∵四边形ABCD是平行四边形(已知)
∴
AO=CO,BO=DO
(平行四边形的对角线互相平分)
∵AE=CF(已知)
∴AO-AE=CO-CF(等式的性质1)
∴EO=FO(等量代换)
又∵
BO=DO(已证)
∴
四边形BFDE是平行四边形
(对角线互相平分的四边形是平行四边形)
A
B
C
D
E
F
O
图18.1-11
课本第46页
例3
知识讲解
难点突破
例3
如图18.1-11,□ABCD的对角线AC、BD相交于点O,E,F是AC上的两点,并且AE=CF。求证:四边形BFDE是平行四边形。
A
B
C
D
E
F
O
图18.1-11
方法二:
两组对边分别相等的四边形是平行四边形
你还有其他证明方法吗?
变式一:如图所示,在□ABCD中,对角线AC、BD相交于点O,
点E,F分别是OA、OC的中点,。求证:四边形BFDE是平行四边形。
A
B
C
D
E
F
O
难点巩固
课堂练习
证明:
∵四边形ABCD是平行四边形(已知)
∴
AO=CO,BO=DO
(平行四边形的对角线互相平分)
∵AE=CF(已知)
∴AO-AE=CO-CF(等式的性质1)
∴EO=FO(等量代换)
又∵
BO=DO(已证)
∴
四边形BFDE是平行四边形
(对角线互相平分的四边形是平行四边形)
又∵E,F分别是AB,CD的中点
∴∴OE=
OA,0F=
OC(线段中点的定义)
并且AE=CF。
如图所示,在□ABCD中,点E,F在对角线AC的延长线上,且AE=CF。求证:四边形BFDE是平行四边形。
变式二
A
B
C
D
E
F
O
课堂练习
难点巩固
证明:
∵四边形ABCD是平行四边形(已知)
∴
AO=CO,BO=DO
(平行四边形的对角线互相平分)
∵AE=CF(已知)
∴AO-AE=CO-CF(等式的性质1)
∴EO=FO(等量代换)
又∵
BO=DO(已证)
∴
四边形BFDE是平行四边形
(对角线互相平分的四边形是平行四边形)
∵AE=CF(已知)
∴AO+AE=CO+CF(等式的性质1)
并且AE=CF。
A
B
C
D
E
F
O
连接BD
B
D
A
C
B
D
A
C
O
平行四边形的判定方法
边
两组对边分别平行的四边形是平行四边形。
两组对边分别相等的四边形是平行四边形。
角
一组对边平行且相等的四边形是平行四边形。
对角线
对角线互相平分的四边形是平行四边形。
平行四边形的判定
两组对角分别相等的四边形是平行四边形。
课堂小结
数学思想方法:合情推理、分类讨论、转化思想
课题:平行四边形的判定
人教版八年级数学下册
第十八章
难点名称:探究并掌握平行四边形的几种判定方法,并能根据平行四边形的判定方法进行合情推理。
目录
CONTENTS
2
B
如图,
取两根等长木条AB、CD,将他们平行放置,再用两根木条BC、AD加固,得到的四边形ABCD是一个平行四边形,想一想这是为什么?
大家齐动手
导入
定义:有两组对边分别平行的四边形叫做平行四边形.
A
B
C
D
四边形ABCD
如果
AB∥CD
AD∥BC
B
D
ABCD
A
C
B
D
A
C
O
平行四边形的性质
边
平行四边形的对边平行
平行四边形的对边相等
角
平行四边形的对角相等
平行四边形的邻角互补
对角线
平行四边形的对角线互相平分
忆——平行四边形的定义与性质
导入
有两组对边分别平行的四边形叫做平行四边形
B
D
A
C
平行四边形的定义
平行四边形的判定定理
∵AB∥CD,AD∥BC(已知)
∴四边形ABCD是平行四边形(两组对边分别平行的四边形是平行四边形)
你能说出下列平行四边形性质的逆命题吗?
①两组对边分别平行的四边形是平行四边形(定义).
②两组对边分别相等的四边形是平行四边形.
③两组对角分别相等的四边形是平行四边形.
④对角线互相平分的四边形是平行四边形.
学
习
新
知
追问:你能根据平行四边形的定义证明这些命题的正确性吗?
已知:如图所示,四边形ABCD中,AB=CD,BC=AD.
求证:四边形ABCD是平行四边形.
在△ABC
和△CDA
中,
A
B
C
D
两组对边分别相等的四边形是平行四边形.
判定定理
猜想1
演绎推理 形成定理
知识讲解
难点突破
证明:连接AC,如图所示,
∴四边形ABCD是平行四边形
∴△ABC≌△CDA(SSS),
∴∠BAC=∠DCA,∠BCA=∠DAC,
∴AB∥CD,AD∥BC,
AB=CD
AC=CA
BC=DA
(两组对边分别平行的四边形是平行四边形)
B
如图,
取两根等长木条AB、CD,将他们平行放置,在用两根木条BC、AD加固,得到的四边形ABCD是一个平行四边形,想一想这是为什么?
大家齐动手
证明:∵ 多边形ABCD是四边形,
∴ ∠A+∠B+∠C+∠D=360°.
如图,在四边形ABCD中,∠A=∠C,∠B=∠D.
求证:四边形ABCD是平行四边形.
演绎推理 形成定理
两组对角分别相等的四边形是平行四边形.
判定定理
猜想2
D
A
B
C
知识讲解
难点突破
又∵ ∠A=∠C,∠B=∠D,
∴ ∠A+∠B=180°,
∠B+∠C=180°.
∴ AD∥BC,AB∥DC.
∴ 四边形ABCD是平行四边形
(两组对边分别平行的四边形是平行四边形)
已知:如图所示,四边形ABCD中,对角线AC与BD交于点O,且OA=OC,OB=OD.求证:四边形ABCD是平行四边形.
对角线互相平分的四边形是平行四边形
证明:在△AOB和△COD中,
B
D
A
C
O
判定定理
难点突破
知识讲解
猜想3
∴△AOB
≌△COD(SAS),
∴四边形ABCD是平行四边形(两组对边分别平行的四边形是平行四边形)
∴AB∥CD
AO=CO
∠AOB=∠COD
BO=DO
∴∠ABO=∠CDO
同理可证AD∥BC
平行四边形的判定
A
B
C
D
1.两组对边分别平行的四边形是平行四边形。
2.两组对边分别相等的四边形是平行四边形。
∵AB=CD,AD=BC(已知)
∴四边形ABCD是平行四边形(两组对边分别相等的四边形是平行四边形)
4.
对角线互相平分的四边形是平行四边形。
∵OA=OC,OB=OD(已知)
∴四边形ABCD是平行四边形(对角线互相平分的四边形是平行四边形)
3.两组对角分别相等的四边形是平行四边形。
∴四边形ABCD是平行四边形(两组对角分别相等的四边形是平行四边形)
∵∠A=∠C,∠B=∠D(已知)
0
A
B
C
D
根据图形,添加一个条件使四边形ABCD是平行四边形.
1.
∵AB=CD
,
.
∴四边形ABCD是平行四边形
2.∵AB//CD
,
.
∴四边形ABCD是平行四边形
3.∵∠A=∠C
,
.
∴四边形ABCD是平行四边形
A
B
C
D
o
4.根据右图填空:
∵四边形对角线AC、BD交于点O.
,
OC=OA
∴四边形ABCD是
.
AD=BC
AD∥BC
∠B=∠C
OD=OB
平行四边形
课堂练习
如图18.1-11,□ABCD的对角线AC、BD相交于点O,E,F是AC上的两点,并且AE=CF。
求证:四边形BFDE是平行四边形。
证明:
∵四边形ABCD是平行四边形(已知)
∴
AO=CO,BO=DO
(平行四边形的对角线互相平分)
∵AE=CF(已知)
∴AO-AE=CO-CF(等式的性质1)
∴EO=FO(等量代换)
又∵
BO=DO(已证)
∴
四边形BFDE是平行四边形
(对角线互相平分的四边形是平行四边形)
A
B
C
D
E
F
O
图18.1-11
课本第46页
例3
知识讲解
难点突破
例3
如图18.1-11,□ABCD的对角线AC、BD相交于点O,E,F是AC上的两点,并且AE=CF。求证:四边形BFDE是平行四边形。
A
B
C
D
E
F
O
图18.1-11
方法二:
两组对边分别相等的四边形是平行四边形
你还有其他证明方法吗?
变式一:如图所示,在□ABCD中,对角线AC、BD相交于点O,
点E,F分别是OA、OC的中点,。求证:四边形BFDE是平行四边形。
A
B
C
D
E
F
O
难点巩固
课堂练习
证明:
∵四边形ABCD是平行四边形(已知)
∴
AO=CO,BO=DO
(平行四边形的对角线互相平分)
∵AE=CF(已知)
∴AO-AE=CO-CF(等式的性质1)
∴EO=FO(等量代换)
又∵
BO=DO(已证)
∴
四边形BFDE是平行四边形
(对角线互相平分的四边形是平行四边形)
又∵E,F分别是AB,CD的中点
∴∴OE=
OA,0F=
OC(线段中点的定义)
并且AE=CF。
如图所示,在□ABCD中,点E,F在对角线AC的延长线上,且AE=CF。求证:四边形BFDE是平行四边形。
变式二
A
B
C
D
E
F
O
课堂练习
难点巩固
证明:
∵四边形ABCD是平行四边形(已知)
∴
AO=CO,BO=DO
(平行四边形的对角线互相平分)
∵AE=CF(已知)
∴AO-AE=CO-CF(等式的性质1)
∴EO=FO(等量代换)
又∵
BO=DO(已证)
∴
四边形BFDE是平行四边形
(对角线互相平分的四边形是平行四边形)
∵AE=CF(已知)
∴AO+AE=CO+CF(等式的性质1)
并且AE=CF。
A
B
C
D
E
F
O
连接BD
B
D
A
C
B
D
A
C
O
平行四边形的判定方法
边
两组对边分别平行的四边形是平行四边形。
两组对边分别相等的四边形是平行四边形。
角
一组对边平行且相等的四边形是平行四边形。
对角线
对角线互相平分的四边形是平行四边形。
平行四边形的判定
两组对角分别相等的四边形是平行四边形。
课堂小结
数学思想方法:合情推理、分类讨论、转化思想
