2020-2021学年人教版数学八年级(下册)18.1.2平行四边形的判定-课件(共14张ppt)
文档属性
| 名称 | 2020-2021学年人教版数学八年级(下册)18.1.2平行四边形的判定-课件(共14张ppt) |

|
|
| 格式 | zip | ||
| 文件大小 | 348.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-04-19 11:19:14 | ||
图片预览



文档简介
(共14张PPT)
18.1.2
平行四边形的判定(1)
复习旧知
平行四边形的定义:
两组对边分别平行的四边形叫做平行四边形.
符号语言:∵AB∥CD,
AD∥BC
∴四边形是平行四边形
A
B
C
D
A
B
C
D
四边形ABCD
如果
AB∥CD
AD∥BC
B
D
ABCD
A
C
B
D
A
C
O
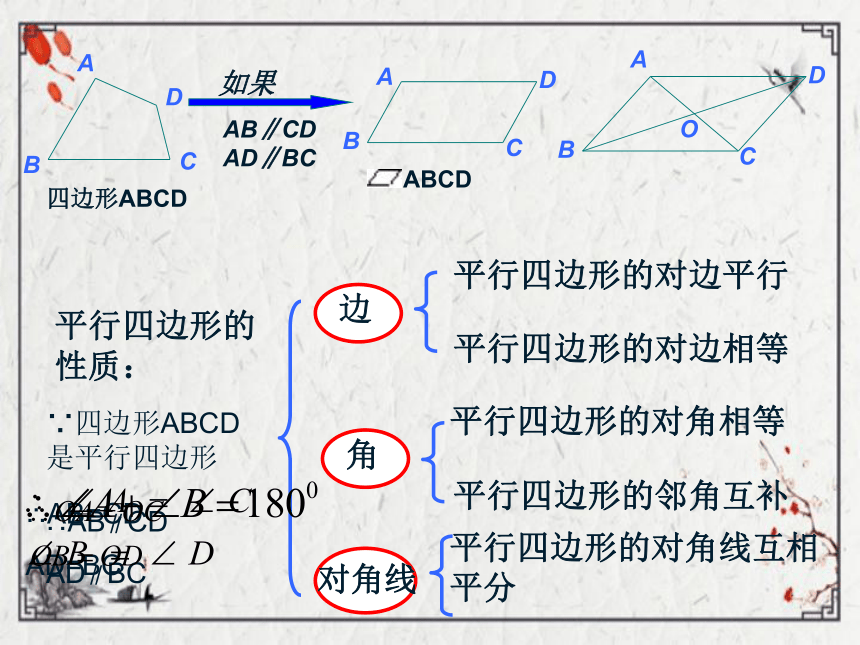
平行四边形的性质:
边
平行四边形的对边平行
平行四边形的对边相等
角
平行四边形的对角相等
平行四边形的邻角互补
对角线
平行四边形的对角线互相平分
∵四边形ABCD
是平行四边形
∴AB=CD
AD=BC
∴AB∥CD
AD∥BC
学行四边形后,小明回家用细木棒钉制了一个。第二天,小明拿着自己动手做的平行四边形向同学们展示。
小辉却问:你凭什么确定这四边形就是平行四边形呢?
大家都困惑了……
请你帮忙
新课引入
B
D
A
C
∠A+
∠B=180
°
AD∥BC
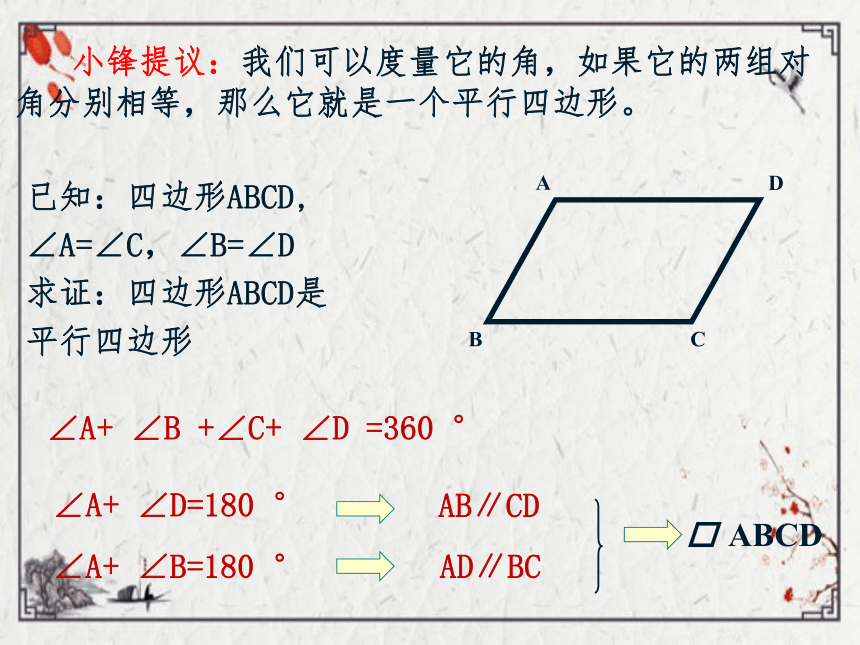
小锋提议:我们可以度量它的角,如果它的两组对角分别相等,那么它就是一个平行四边形。
已知:四边形ABCD,
∠A=∠C,∠B=∠D
求证:四边形ABCD是
平行四边形
ABCD
∠A+
∠D=180
°
AB∥CD
∠A+
∠B
+∠C+
∠D
=360
°
B
D
A
C
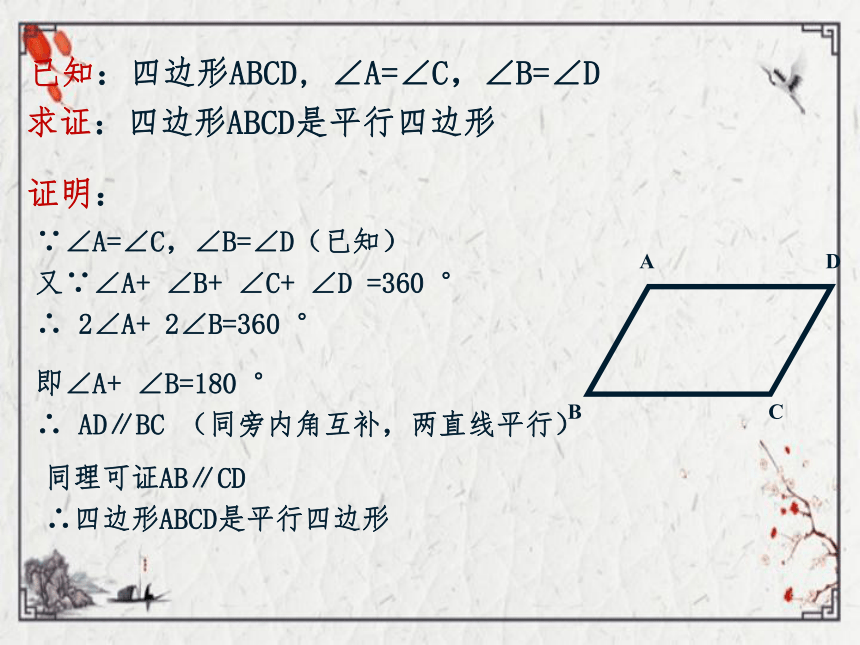
已知:四边形ABCD,
∠A=∠C,∠B=∠D
求证:四边形ABCD是平行四边形
∵∠A=∠C,∠B=∠D(已知)
又∵∠A+
∠B+
∠C+
∠D
=360
°
∴
2∠A+
2∠B=360
°
证明:
即∠A+
∠B=180
°
∴
AD∥BC
(同旁内角互补,两直线平行)
同理可证AB∥CD
∴四边形ABCD是平行四边形
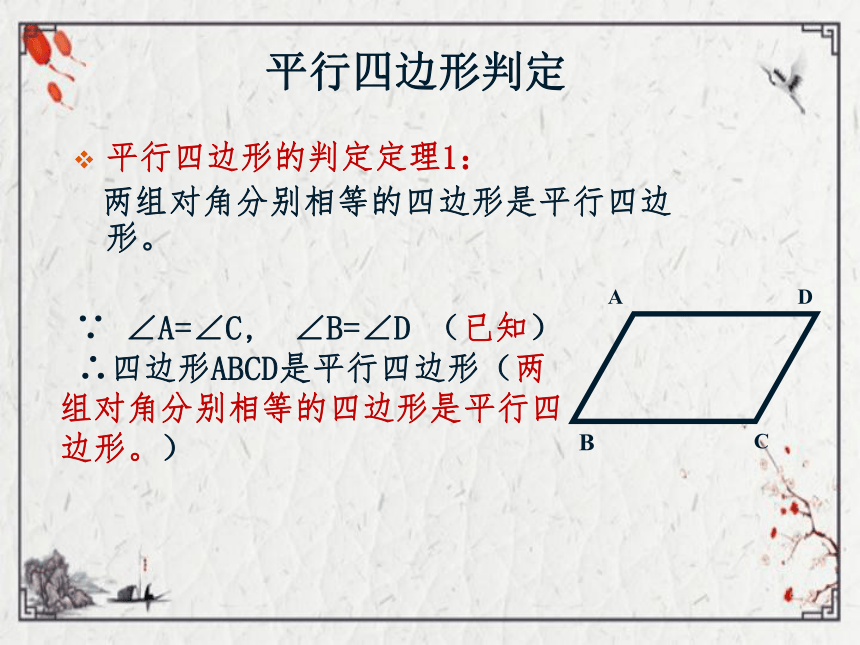
平行四边形判定
平行四边形的判定定理1:
两组对角分别相等的四边形是平行四边形。
∵
∠A=∠C,
∠B=∠D
(已知)
∴四边形ABCD是平行四边形(两
组对角分别相等的四边形是平行四边形。)
A
B
C
D
请你识别下列四边形是否是平行四边形?请说明理由?
A
D
C
B
110°
70°
110°
例1
1.如图,AB=DC=EF,AD=BC,DE=CF.图中互相平行的线段有:
拓展训练
判定
文字语言
图形语言
符号语言
定义
两组对边分别平行的四边形是平行四边形
∵AB∥CD,
AD∥BC
∴四边形是平行四边形
定理1
两组对角分别相等的四边形是平行四边形
∵∠A=∠C,
∠B=∠D
∴四边形是平行四边形
A
B
C
D
A
B
C
D
课堂小结
2、如图,在四边形ABCD中,∠A+∠B=180,∠A=∠C,求证:四边形ABCD是平行四边形。
拓展训练
A
B
C
D
3.已知:如图,在ABCD中,AE、CF分别是∠DAB、∠BCD的平分线.
求证:四边形AFCE是平行四边形.
拓展训练
A
D
F
E
B
C
布置作业
布置作业:
1.必做题:(P50,习题18.1,第4题)
2.选做题(任选一题):(P50,习题18.1,第5、6题)
3.预习:探究---还有什么方法可以判定一个四边形是平行四边形?
(设计意图:在布置作业时给出有梯度的练习,为的是满足不同层次学生学习的需要。而且通作业“预习”的探究,让学生发现平行四边形更多的判定方法。为下节课进一步探究平行四边形的其他判定方法奠定基础。)
Thanks!
感谢各位老师批评指导
18.1.2
平行四边形的判定(1)
复习旧知
平行四边形的定义:
两组对边分别平行的四边形叫做平行四边形.
符号语言:∵AB∥CD,
AD∥BC
∴四边形是平行四边形
A
B
C
D
A
B
C
D
四边形ABCD
如果
AB∥CD
AD∥BC
B
D
ABCD
A
C
B
D
A
C
O
平行四边形的性质:
边
平行四边形的对边平行
平行四边形的对边相等
角
平行四边形的对角相等
平行四边形的邻角互补
对角线
平行四边形的对角线互相平分
∵四边形ABCD
是平行四边形
∴AB=CD
AD=BC
∴AB∥CD
AD∥BC
学行四边形后,小明回家用细木棒钉制了一个。第二天,小明拿着自己动手做的平行四边形向同学们展示。
小辉却问:你凭什么确定这四边形就是平行四边形呢?
大家都困惑了……
请你帮忙
新课引入
B
D
A
C
∠A+
∠B=180
°
AD∥BC
小锋提议:我们可以度量它的角,如果它的两组对角分别相等,那么它就是一个平行四边形。
已知:四边形ABCD,
∠A=∠C,∠B=∠D
求证:四边形ABCD是
平行四边形
ABCD
∠A+
∠D=180
°
AB∥CD
∠A+
∠B
+∠C+
∠D
=360
°
B
D
A
C
已知:四边形ABCD,
∠A=∠C,∠B=∠D
求证:四边形ABCD是平行四边形
∵∠A=∠C,∠B=∠D(已知)
又∵∠A+
∠B+
∠C+
∠D
=360
°
∴
2∠A+
2∠B=360
°
证明:
即∠A+
∠B=180
°
∴
AD∥BC
(同旁内角互补,两直线平行)
同理可证AB∥CD
∴四边形ABCD是平行四边形
平行四边形判定
平行四边形的判定定理1:
两组对角分别相等的四边形是平行四边形。
∵
∠A=∠C,
∠B=∠D
(已知)
∴四边形ABCD是平行四边形(两
组对角分别相等的四边形是平行四边形。)
A
B
C
D
请你识别下列四边形是否是平行四边形?请说明理由?
A
D
C
B
110°
70°
110°
例1
1.如图,AB=DC=EF,AD=BC,DE=CF.图中互相平行的线段有:
拓展训练
判定
文字语言
图形语言
符号语言
定义
两组对边分别平行的四边形是平行四边形
∵AB∥CD,
AD∥BC
∴四边形是平行四边形
定理1
两组对角分别相等的四边形是平行四边形
∵∠A=∠C,
∠B=∠D
∴四边形是平行四边形
A
B
C
D
A
B
C
D
课堂小结
2、如图,在四边形ABCD中,∠A+∠B=180,∠A=∠C,求证:四边形ABCD是平行四边形。
拓展训练
A
B
C
D
3.已知:如图,在ABCD中,AE、CF分别是∠DAB、∠BCD的平分线.
求证:四边形AFCE是平行四边形.
拓展训练
A
D
F
E
B
C
布置作业
布置作业:
1.必做题:(P50,习题18.1,第4题)
2.选做题(任选一题):(P50,习题18.1,第5、6题)
3.预习:探究---还有什么方法可以判定一个四边形是平行四边形?
(设计意图:在布置作业时给出有梯度的练习,为的是满足不同层次学生学习的需要。而且通作业“预习”的探究,让学生发现平行四边形更多的判定方法。为下节课进一步探究平行四边形的其他判定方法奠定基础。)
Thanks!
感谢各位老师批评指导
