2020-2021学年七年级数学苏科版下册-12.1 定义与命题(75)-课件(共30张ppt)
文档属性
| 名称 | 2020-2021学年七年级数学苏科版下册-12.1 定义与命题(75)-课件(共30张ppt) |  | |
| 格式 | zip | ||
| 文件大小 | 289.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-04-19 11:10:21 | ||
图片预览











文档简介
(共30张PPT)
12.1
定义与命题
思考:白云和黑土所说的“暗送秋波”是同一个含义吗?
情境归纳
日常生活中,人们为了交流,常常用到一些名称和术语,经常要判断事物的对与错、是与非、可能与不可能等.只有对这些名称和术语有了共识,才可以正常交流.在数学中要进行说理,必须对涉及的概念有共识,也就是需要对概念下定义.
具体什么叫做定义呢?
活动一
概念学习
对名称和术语的含义进行描述、做出规定,就是给出它们的定义.
术语
[shù
yǔ]
释义
专门学科的专门用语
例如:
1、“由3条不在同一直线上的线段,首尾依次相接组成的
图形是三角形”,是
的定义。
2、“在一个方程中,只含有一个未知数,并且未知数的最
高次数是1,像这样的方程叫做一元一次方程”是
的定义。
三角形
一元一次方程
考考你
请说出下列名词的定义:
(1)平行线:
(2)绝对值:
在同一平面内,不相交的两条直线。
数轴上表示一个数的点到原点的距离。
(3)方程的解:
能使方程两边的值相等的未知数的值。
相信自己行,你就行!
说一说:你还能说出哪些
数学名称或术语的定义吗?
做
一
做
?
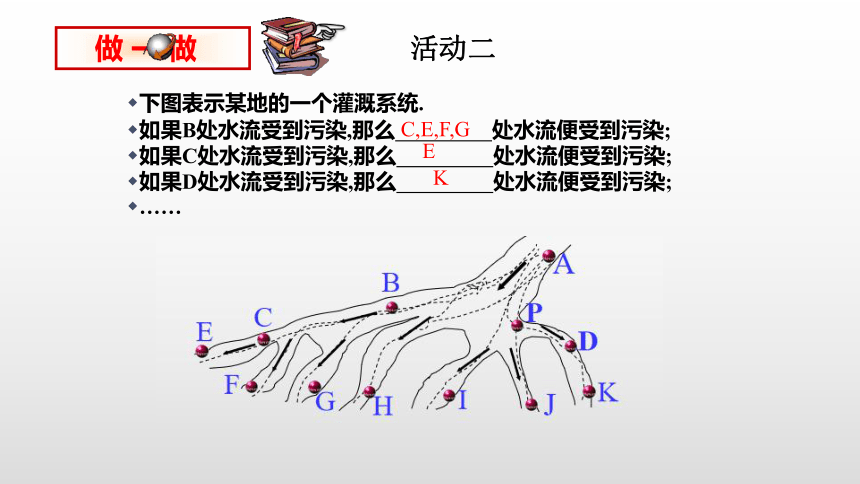
下图表示某地的一个灌溉系统.
如果B处水流受到污染,那么
处水流便受到污染;
如果C处水流受到污染,那么
处水流便受到污染;
如果D处水流受到污染,那么
处水流便受到污染;
……
C,E,F,G
E
K
活动二
想
一
想
?
如果B处水流受到污染,那么C、E、F、G处水流便受到污染;
如果C处水流受到污染,那么
E
处水流便受到污染;
如果D处水流受到污染,那么
K
处水流便受到污染;
上面“如果……那么……”,都是对事情进行判断的句子
上面的句子,有什么共同的特征?
比较下列句子在表述形式上哪些对事情作了判断?哪些没有对事情作出判断?
(1)鸟是动物;
(2)若a2=4,求a的值;
(3)若a2=b2,则a=b;
(4)a、b两条直线平行吗?
(5)画一个角等于已知角;
(6)0.33是无理数;
(7)两直线平行,同位角相等.
辨
一
辨
?
判断一件事情的句子叫做命题.
命题(proposition):
命题的定义
?
命题的定义中体现了以下两层含义:
(1)命题必须是完整的句子.
(2)这个句子必须对某一事物做出明确的肯定或否定的判断.命题中,不存在“大约”、“大概”、“差不多”、“左右”等含糊不清的词语.
归
纳
?
2)两条直线相交,有且只有一个交点(
)
4)一个平角的度数是180度(
)
6)取线段AB的中点C;(
)
1)长度相等的两条线段是相等的线段吗?(
)
7)画两条相等的线段(
)
判断下列语句是不是命题?是用“√”,不是用“×
表示。
3)不相等的两个角不是对顶角(
)
5)相等的两个角是对顶角(
)
×
√
×
×
√
√
√
判断一个句子是不是命题的关键是什么?
是否作出判断
8)两直线平行,同位角相等;(
)
√
命题:
两直线平行,同位角相等.
条件
结论
(题设)
在数学中,命题一般可看作由题设(条件)
和结论两部分组成,题设是已知事项,结论是
由已知事项推出的事项.
(结论)
【命题的结构】
活动三
下列各命题的条件是什么?结论是什么?
1、如果a、b两数的积为0,那么a、b两数都为0;
2、如果两个角互为补角,那么这两角和为180°;
3、两直线平行,同旁内角互补;
4、直角三角形的两个锐角互余;
5、有公共端点的两个角是对顶角
.
做一做
?
条件
结论
1
2
3
4
5
a、b两数的积为0
a、b两数都为0
两个角互为补角
这两角和为180°
两直线平行
同旁内角互补
两个角是直角三角形的两个锐角
这两个角互余
有公共端点的两个角
这两个角是对顶角
方法:
先结论,
后条件.
相等
对顶角
(两个角是)
条件:
(补上适当词语)
结论:
角
两个
(1)对顶角相等
条件:两个角是对顶角,
结论:这两个角相等.
找出下列命题的条件和结论.
【例题】
如果两个角是对顶角,那么这两个角相等.
改写:
方法:
先结论,
后条件.
命题
条件
结论
如果a>0,b>0,那么a-b>0
同位角相等,两直线平行
等角的余角相等
注意:将命题改写成”如果……那么……”的形式,“如果”后面的部分是条件,“那么”后面的部分是结论.
练习.把下列命题改写成“如果……那么……”的形式,并写出命题的条件和结论.
如果一个四边形是正方形,那么它的四条边相等
改写成:
条件是:
结论是:
一个四边形是正方形
它的四条边相等
(1)若a>b,则ac>bc.
改写成:
条件是:
结论是:
如果a>b,那么ac>bc.
(2)正方形的四条边相等
a>b
ac>bc
(3)钝角大于它的补角;
(4)等角的余角相等
改写成:
条件是:
结论是:
改写成:
条件是:
结论是:
如果一个角是钝角,那么这个角大于这个角的补角
一个角是钝角
这个角大于这个角的补角
如果两个角相等,那么这两个角的余角也相等
两个角相等
这两个角的余角也相等
命题组成
条件
结论
组成剖析
已知事项
由已知事项推出的事项
表达形式
如果……
那么……
归
纳
?
如果______成立,那么___________,
像这样的命题叫做真命题.
_____成立,_____________________________,
像这样的命题叫做假命题.
条件
结论成立
条件
结论不成立
要说明一个命题是假命题,通常可以举出一个例子,使之具备命题的条件,而不具备命题的结论,这种例子称为反例.
活动四
下列各命题的条件是什么?结论是什么?哪些是真命题?哪些是假命题?
(1)如果a<0,b<0,那么a+b<0;
解:命题的条件:a<0,b<0;
结论:a+b<0.
解:命题的条件:一个数平方后等于4;
结论:这个数是2.
这个命题是真命题.
这个命题是假命题.
练一练
(2)平方后等于4的数是2;
下列各命题的条件是什么?结论是什么?哪些是真命题?哪些是假命题?
(3)同角的补角相等
(4)直角都相等
解:命题的条件:两个角是同一个角的补角;
结论:这两个角相等.
这个命题是真命题.
这个命题是真命题.
解:命题的条件:几个角都是直角;
结论:这几个角相等.
练一练
真命题假命题的比较
:
真命题
如果条件成立,那么结论一定成立.
假命题
条件成立时,不能保证结论总是正确的.
归
纳
?
拓展提升
1.在数学运算中,除了加、减、乘、除等运算外,还可以定义新的运算。如定义一种“星”运算,“
”是它的运算符号,其运算法则是:
于是:
按以上定义,填空:
___
___
请你参照以上方法,也定义一种新运算,并举几个运算的例子。
2.
下列句子中,哪些是命题?哪些不是命题?
(1)正数大于一切负数吗?
(2)两点之间线段最短。
(3)0是自然数。
(4)作一条直线和已知直线平行。
(5)相等的角是对顶角;
(√)
(√)
(×)
(×)
(√)
3.在第1题中,_______是真命题,________假命题.
(2)(3)
(5)
拓展提升
(1)若a∥b,b∥c,则a∥c
;
(2)如果a是有理数,则
a2
+1>0
;
(3)若a2>b2
,则
a>b
;
(4)若
ab=0
,则a=0
;
(5)如果两个角的两边互相平行,这两个角一定相等;
(6)绝对值等于它本身的数是正数.
4.下列命题是真命题?还是假命题?
拓展提升
5.
指出下列命题的条件和结论,并改写成
“如果……那么……”的形式:
(1)如果a>b,a>c,那么b=c.
(2)直角三角形两个锐角互余。
(3)对顶角相等
(4)π是无理数
拓展提升
命题让我们的社会发展,进步.
定义让我们的世界规范,和谐.
规定意义
已知
已知
命题:
推出
条件
(已知)
结论
(未知)
正确
不正确
发展
定义:
小
结
?
真命题
假命题
1.课本145页练一练,
2.课本12.1习题第1、2、3题;
布置作业
?
谢
谢!
12.1
定义与命题
思考:白云和黑土所说的“暗送秋波”是同一个含义吗?
情境归纳
日常生活中,人们为了交流,常常用到一些名称和术语,经常要判断事物的对与错、是与非、可能与不可能等.只有对这些名称和术语有了共识,才可以正常交流.在数学中要进行说理,必须对涉及的概念有共识,也就是需要对概念下定义.
具体什么叫做定义呢?
活动一
概念学习
对名称和术语的含义进行描述、做出规定,就是给出它们的定义.
术语
[shù
yǔ]
释义
专门学科的专门用语
例如:
1、“由3条不在同一直线上的线段,首尾依次相接组成的
图形是三角形”,是
的定义。
2、“在一个方程中,只含有一个未知数,并且未知数的最
高次数是1,像这样的方程叫做一元一次方程”是
的定义。
三角形
一元一次方程
考考你
请说出下列名词的定义:
(1)平行线:
(2)绝对值:
在同一平面内,不相交的两条直线。
数轴上表示一个数的点到原点的距离。
(3)方程的解:
能使方程两边的值相等的未知数的值。
相信自己行,你就行!
说一说:你还能说出哪些
数学名称或术语的定义吗?
做
一
做
?
下图表示某地的一个灌溉系统.
如果B处水流受到污染,那么
处水流便受到污染;
如果C处水流受到污染,那么
处水流便受到污染;
如果D处水流受到污染,那么
处水流便受到污染;
……
C,E,F,G
E
K
活动二
想
一
想
?
如果B处水流受到污染,那么C、E、F、G处水流便受到污染;
如果C处水流受到污染,那么
E
处水流便受到污染;
如果D处水流受到污染,那么
K
处水流便受到污染;
上面“如果……那么……”,都是对事情进行判断的句子
上面的句子,有什么共同的特征?
比较下列句子在表述形式上哪些对事情作了判断?哪些没有对事情作出判断?
(1)鸟是动物;
(2)若a2=4,求a的值;
(3)若a2=b2,则a=b;
(4)a、b两条直线平行吗?
(5)画一个角等于已知角;
(6)0.33是无理数;
(7)两直线平行,同位角相等.
辨
一
辨
?
判断一件事情的句子叫做命题.
命题(proposition):
命题的定义
?
命题的定义中体现了以下两层含义:
(1)命题必须是完整的句子.
(2)这个句子必须对某一事物做出明确的肯定或否定的判断.命题中,不存在“大约”、“大概”、“差不多”、“左右”等含糊不清的词语.
归
纳
?
2)两条直线相交,有且只有一个交点(
)
4)一个平角的度数是180度(
)
6)取线段AB的中点C;(
)
1)长度相等的两条线段是相等的线段吗?(
)
7)画两条相等的线段(
)
判断下列语句是不是命题?是用“√”,不是用“×
表示。
3)不相等的两个角不是对顶角(
)
5)相等的两个角是对顶角(
)
×
√
×
×
√
√
√
判断一个句子是不是命题的关键是什么?
是否作出判断
8)两直线平行,同位角相等;(
)
√
命题:
两直线平行,同位角相等.
条件
结论
(题设)
在数学中,命题一般可看作由题设(条件)
和结论两部分组成,题设是已知事项,结论是
由已知事项推出的事项.
(结论)
【命题的结构】
活动三
下列各命题的条件是什么?结论是什么?
1、如果a、b两数的积为0,那么a、b两数都为0;
2、如果两个角互为补角,那么这两角和为180°;
3、两直线平行,同旁内角互补;
4、直角三角形的两个锐角互余;
5、有公共端点的两个角是对顶角
.
做一做
?
条件
结论
1
2
3
4
5
a、b两数的积为0
a、b两数都为0
两个角互为补角
这两角和为180°
两直线平行
同旁内角互补
两个角是直角三角形的两个锐角
这两个角互余
有公共端点的两个角
这两个角是对顶角
方法:
先结论,
后条件.
相等
对顶角
(两个角是)
条件:
(补上适当词语)
结论:
角
两个
(1)对顶角相等
条件:两个角是对顶角,
结论:这两个角相等.
找出下列命题的条件和结论.
【例题】
如果两个角是对顶角,那么这两个角相等.
改写:
方法:
先结论,
后条件.
命题
条件
结论
如果a>0,b>0,那么a-b>0
同位角相等,两直线平行
等角的余角相等
注意:将命题改写成”如果……那么……”的形式,“如果”后面的部分是条件,“那么”后面的部分是结论.
练习.把下列命题改写成“如果……那么……”的形式,并写出命题的条件和结论.
如果一个四边形是正方形,那么它的四条边相等
改写成:
条件是:
结论是:
一个四边形是正方形
它的四条边相等
(1)若a>b,则ac>bc.
改写成:
条件是:
结论是:
如果a>b,那么ac>bc.
(2)正方形的四条边相等
a>b
ac>bc
(3)钝角大于它的补角;
(4)等角的余角相等
改写成:
条件是:
结论是:
改写成:
条件是:
结论是:
如果一个角是钝角,那么这个角大于这个角的补角
一个角是钝角
这个角大于这个角的补角
如果两个角相等,那么这两个角的余角也相等
两个角相等
这两个角的余角也相等
命题组成
条件
结论
组成剖析
已知事项
由已知事项推出的事项
表达形式
如果……
那么……
归
纳
?
如果______成立,那么___________,
像这样的命题叫做真命题.
_____成立,_____________________________,
像这样的命题叫做假命题.
条件
结论成立
条件
结论不成立
要说明一个命题是假命题,通常可以举出一个例子,使之具备命题的条件,而不具备命题的结论,这种例子称为反例.
活动四
下列各命题的条件是什么?结论是什么?哪些是真命题?哪些是假命题?
(1)如果a<0,b<0,那么a+b<0;
解:命题的条件:a<0,b<0;
结论:a+b<0.
解:命题的条件:一个数平方后等于4;
结论:这个数是2.
这个命题是真命题.
这个命题是假命题.
练一练
(2)平方后等于4的数是2;
下列各命题的条件是什么?结论是什么?哪些是真命题?哪些是假命题?
(3)同角的补角相等
(4)直角都相等
解:命题的条件:两个角是同一个角的补角;
结论:这两个角相等.
这个命题是真命题.
这个命题是真命题.
解:命题的条件:几个角都是直角;
结论:这几个角相等.
练一练
真命题假命题的比较
:
真命题
如果条件成立,那么结论一定成立.
假命题
条件成立时,不能保证结论总是正确的.
归
纳
?
拓展提升
1.在数学运算中,除了加、减、乘、除等运算外,还可以定义新的运算。如定义一种“星”运算,“
”是它的运算符号,其运算法则是:
于是:
按以上定义,填空:
___
___
请你参照以上方法,也定义一种新运算,并举几个运算的例子。
2.
下列句子中,哪些是命题?哪些不是命题?
(1)正数大于一切负数吗?
(2)两点之间线段最短。
(3)0是自然数。
(4)作一条直线和已知直线平行。
(5)相等的角是对顶角;
(√)
(√)
(×)
(×)
(√)
3.在第1题中,_______是真命题,________假命题.
(2)(3)
(5)
拓展提升
(1)若a∥b,b∥c,则a∥c
;
(2)如果a是有理数,则
a2
+1>0
;
(3)若a2>b2
,则
a>b
;
(4)若
ab=0
,则a=0
;
(5)如果两个角的两边互相平行,这两个角一定相等;
(6)绝对值等于它本身的数是正数.
4.下列命题是真命题?还是假命题?
拓展提升
5.
指出下列命题的条件和结论,并改写成
“如果……那么……”的形式:
(1)如果a>b,a>c,那么b=c.
(2)直角三角形两个锐角互余。
(3)对顶角相等
(4)π是无理数
拓展提升
命题让我们的社会发展,进步.
定义让我们的世界规范,和谐.
规定意义
已知
已知
命题:
推出
条件
(已知)
结论
(未知)
正确
不正确
发展
定义:
小
结
?
真命题
假命题
1.课本145页练一练,
2.课本12.1习题第1、2、3题;
布置作业
?
谢
谢!
同课章节目录
- 第7章 平面图形的认识(二)
- 7.1 探索直线平行的条件
- 7.2 探索平行线的性质
- 7.3 图形的平移
- 7.4 认识三角形
- 7.5 多边形的内角和与外角和
- 第8章 幂的运算
- 8.1 同底数幂的乘法
- 8.2 幂的乘方与积的乘方
- 8.3 同底数幂的除法
- 第9章 整式乘法与因式分解
- 9.1 单项式乘单项式
- 9.2 单项式乘多项式
- 9.3 多项式乘多项式
- 9.4 乘法公式
- 9.5 多项式的因式分解
- 第10章 二元一次方程组
- 10.1 二元一次方程
- 10.2 二元一次方程组
- 10.3 解二元一次方程组
- 10.4 三元一次方程组
- 10.5 用二元一次方程解决问题
- 第11章 一元一次不等式
- 11.1 生活中的不等式
- 11.2 不等式的解集
- 11.3 不等式的性质
- 11.4 解一元一次不等式
- 11.5 用一元一次不等式解决问题
- 11.6 一元一次不等式组
- 第12章 证明
- 12.1 定义与命题
- 12.2 证明
- 12.3 互逆命题
