第19章 一元二次方程单元测试(二)及答案
文档属性
| 名称 | 第19章 一元二次方程单元测试(二)及答案 |  | |
| 格式 | zip | ||
| 文件大小 | 67.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2012-02-26 12:04:56 | ||
图片预览


文档简介
第十九章 一元二次方程水平测试(二)
一、精心选一选(每小题3分,共24分)
1.解方程2(x-3)2-3x(x-3)=0的最适当的方法应是( )
A.直接开平方法 B.配方法 C.公式法 D.因式分解法
2.方程(x-5)(x+2)=-10的解是( )
A.5 B.-2 C.-2或5 D.以上都不对
3.已知(m-1)x2+2mx+(m-1)=0有两个不相等的实数根,则m的取值范围是( )
A.m> B.m<且m≠1 C.m>且m≠1 D.<m<1
4.若n(n≠0)是关于x的方程x2+mx+2n=0的根,则m+n的值为( )
A.1 B.2 C.-1 D.-2
5.关于x的方程ax2-(a+2)x+2=0只有一解(相同解算一解),则a的值为( )
A.a=0 B.a=2 C.a=1 D.a=0或a=2
6.如图1,在□ABCD中,AE⊥BC于E,AE=EB=EC=a,且a是一元二次方程x2+2x-3=0的根,则□ABCD的周长为( )
A.4+2 B.12+6 C.2+2 D.2+或12+6
7.一个小组有若干人,新年互送贺年片一张,已知全组共送贺年片72张,则这个小组有( )
A.12人 B.18人 C.9人 D.10
8.如图2,直线y=kx+b经过A(-2,-1)和B(-3,0)两点,利用函数图象判断不等式<kx+b的解集为( )
A.x<或x> B.<x<
C.<x< D.x<或<x<0
二、细心填一填(每小题4分,共24分)
9.方程x(x+1)=2(x+1)的解是x=______.
10.写出一个以-1,2为根的一元二次方程______.
11.如果关于x的方程x2-x+k=0(k为常数)有两个相等的实数根,那么k=______.
12.等腰△ABC两边的长分别是一元二次方程x2-5x+6=0的两个解,则这个等腰三角形的周长是 .
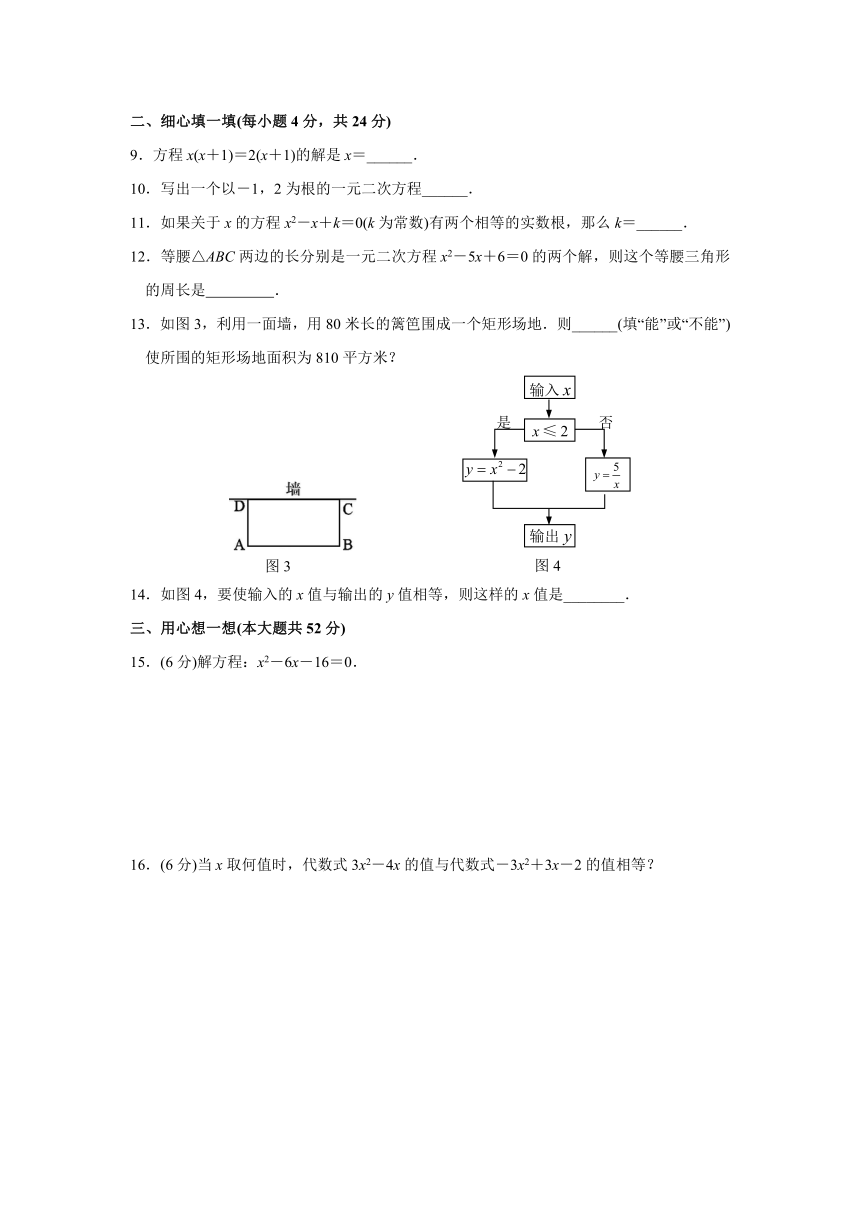
13.如图3,利用一面墙,用80米长的篱笆围成一个矩形场地.则______(填“能”或“不能”)使所围的矩形场地面积为810平方米?
14.如图4,要使输入的x值与输出的y值相等,则这样的x值是________.
三、用心想一想(本大题共52分)
15.(6分)解方程:x2-6x-16=0.
16.(6分)当x取何值时,代数式3x2-4x的值与代数式-3x2+3x-2的值相等?
17.(6分)已知关于x的一元二次方程x2-mx-2=0.①
(1)若x=-1是方程①的一个根,求m的值和方程①的另一根;
(2)对于任意实数m,判断方程①的根的情况,并说明理由.
18.(8分)某商店购进一种商品,单价30元.试销中发现这种商品每天的销售量p(件)与每件的销售价x(元)满足关系:p=100-2x.若商店每天销售这种商品要获得200元的利润,那么每件商品的售价应定为多少元?每天要售出这种商品多少件?
19.(8分)(09天津市)注意:为了使同学们更好地解答本题,我们提供了一种解题思路,你可以依照这个思路填空,并完成本题解答的全过程.如果你选用其他的解题方案,此时,不必填空,只需按照解答题的一般要求,进行解答即可.
如图5(1),要设计一幅宽20cm,长30cm的矩形图案,其中有两横两竖的彩条,横、竖彩条的宽度比为2∶3,如果要使所有彩条所占面积为原矩形图案面积的三分之一,应如何设计每个彩条的宽度?
分析:由横、竖彩条的宽度比为2∶3,可设每个横彩条的宽为2x,则每个竖彩条的宽为3x.为更好地寻找题目中的等量关系,将横、竖彩条分别集中,原问题转化为如图5(2)的情况,得到矩形ABCD.
结合以上分析完成填空:如图5(2),用含x的代数式表示:AB=__________cm;AD=__________cm;矩形ABCD的面积为__________cm2;列出方程并完成本题解答.
20.(8分)已知关于x的一元二次方程x2+(2m-1)x+m2=0有两个实数根x1和x2.
(1)求实数m的取值范围;(2)当x12-x22=0时,求m的值.(友情提示:若x1,x2是一元二次方程ax2+bx+c=0(a≠0)两根,则有x1+x2=,x1x2=)
21.(10分)(09安徽省)如图6,将正方形沿图中虚线(其中x<y)剪成①②③④四块图形,用这四块图形恰能拼成一个矩形(非正方形).画出拼成的矩形的简图;求的值.
参考答案
1.D 2.D 3.C 4.B 5.D 6.A
7.C提示:设有x人,则x(x-1)=72 8.D 9.-1或2
10.答案不唯一,如(x+1)(x-2)=0,即x2-x-2=0
11. 12.7或8
13.不能 提示:设AD=BC=xm,则AB=(80-2x)m.
由题意得:x(80-2x)=810.△=402-4×405=1600-1620=-20<0.
∴方程无解,故不能围成面积为810m2的矩形场地
14.-1,2, 提示:令x2-2=x(x≤2),解得x1=-1,x2=2.
这两解均符合条件x≤2;再令=x(x>2),解得x=.
但x=不符合条件x>2,∴舍去x=.故所求x的值为-1,2,
15.解:原方程分解因式得(x+2)(x-8)=0,∴x1=-2,x2=8
16.解:依题意得3x2-4x=-3x2+3x-2,即6x2-7x+2=0.
分解因式得(2x-1)(3x-2)=0,所以x=或x=
17.解:(1)x=-1是方程①的一个根,所以1+m-2=0,解得m=1.
方程变为x2-x-2=0,解得,x1=-1,x2=2.
所以方程的另一根为x=2.
(2)b2-4ac=m2+8,因为对于任意实数m,m2≥0,所以m2+8>0,
所以对于任意的实数m,方程①有两个不相等的实数根
18.解:根据题意得:(x-30)(100-2x)=200.整理得:x2-80x+1600=0.
∴(x-40)2=0,x=40(元).于是p=100-2x=20(件).
答:每件商品的售价应定为40元,每天要销售这种商品20件
19.解:(1)20-6x,30-4x,24x2-260x+600;
(2)根据题意,得24x2-260x+600=(1-)×20×30.整理,得6x2-65x+50=0.
解方程,得x1=,x2=10(不合题意,舍去).则2x=,3x=.
答:每个横、竖彩条的宽度分别为cm,cm
20.解:(1)由题意有△=(2m-1)2-4m2≥0,解得m≤.即实数m的取值范围是m≤.
(2)由x12-x22=0得(x1+x2)(x1-x2)=0.若x1+x2=0,即-(2m-1)=0,解得m=.
∵>,∴m=不合题意,舍去.若x1-x2=0,即x1=x2,∴△=0,
由(1)知m=.故当x12-x22=0时,m=
21.解:(1)如图.说明:其它正确拼法可相应赋分.
(2)解法一:由拼图前后的面积相等得:[(x+y)+y]y=(x+y)2.
因为y≠0,整理得:.解得:=(负值不合题意,舍去).
解法二:由拼成的矩形可知:=.以下同解法一.
图1
图2
图3
输入
输出
HYPERLINK "http://" EMBED Equation.DSMT4
是
否
图4
20cm
20cm
30cm
D
C
A
B
图5(2)
图5(1)
30cm
图6
一、精心选一选(每小题3分,共24分)
1.解方程2(x-3)2-3x(x-3)=0的最适当的方法应是( )
A.直接开平方法 B.配方法 C.公式法 D.因式分解法
2.方程(x-5)(x+2)=-10的解是( )
A.5 B.-2 C.-2或5 D.以上都不对
3.已知(m-1)x2+2mx+(m-1)=0有两个不相等的实数根,则m的取值范围是( )
A.m> B.m<且m≠1 C.m>且m≠1 D.<m<1
4.若n(n≠0)是关于x的方程x2+mx+2n=0的根,则m+n的值为( )
A.1 B.2 C.-1 D.-2
5.关于x的方程ax2-(a+2)x+2=0只有一解(相同解算一解),则a的值为( )
A.a=0 B.a=2 C.a=1 D.a=0或a=2
6.如图1,在□ABCD中,AE⊥BC于E,AE=EB=EC=a,且a是一元二次方程x2+2x-3=0的根,则□ABCD的周长为( )
A.4+2 B.12+6 C.2+2 D.2+或12+6
7.一个小组有若干人,新年互送贺年片一张,已知全组共送贺年片72张,则这个小组有( )
A.12人 B.18人 C.9人 D.10
8.如图2,直线y=kx+b经过A(-2,-1)和B(-3,0)两点,利用函数图象判断不等式<kx+b的解集为( )
A.x<或x> B.<x<
C.<x< D.x<或<x<0
二、细心填一填(每小题4分,共24分)
9.方程x(x+1)=2(x+1)的解是x=______.
10.写出一个以-1,2为根的一元二次方程______.
11.如果关于x的方程x2-x+k=0(k为常数)有两个相等的实数根,那么k=______.
12.等腰△ABC两边的长分别是一元二次方程x2-5x+6=0的两个解,则这个等腰三角形的周长是 .
13.如图3,利用一面墙,用80米长的篱笆围成一个矩形场地.则______(填“能”或“不能”)使所围的矩形场地面积为810平方米?
14.如图4,要使输入的x值与输出的y值相等,则这样的x值是________.
三、用心想一想(本大题共52分)
15.(6分)解方程:x2-6x-16=0.
16.(6分)当x取何值时,代数式3x2-4x的值与代数式-3x2+3x-2的值相等?
17.(6分)已知关于x的一元二次方程x2-mx-2=0.①
(1)若x=-1是方程①的一个根,求m的值和方程①的另一根;
(2)对于任意实数m,判断方程①的根的情况,并说明理由.
18.(8分)某商店购进一种商品,单价30元.试销中发现这种商品每天的销售量p(件)与每件的销售价x(元)满足关系:p=100-2x.若商店每天销售这种商品要获得200元的利润,那么每件商品的售价应定为多少元?每天要售出这种商品多少件?
19.(8分)(09天津市)注意:为了使同学们更好地解答本题,我们提供了一种解题思路,你可以依照这个思路填空,并完成本题解答的全过程.如果你选用其他的解题方案,此时,不必填空,只需按照解答题的一般要求,进行解答即可.
如图5(1),要设计一幅宽20cm,长30cm的矩形图案,其中有两横两竖的彩条,横、竖彩条的宽度比为2∶3,如果要使所有彩条所占面积为原矩形图案面积的三分之一,应如何设计每个彩条的宽度?
分析:由横、竖彩条的宽度比为2∶3,可设每个横彩条的宽为2x,则每个竖彩条的宽为3x.为更好地寻找题目中的等量关系,将横、竖彩条分别集中,原问题转化为如图5(2)的情况,得到矩形ABCD.
结合以上分析完成填空:如图5(2),用含x的代数式表示:AB=__________cm;AD=__________cm;矩形ABCD的面积为__________cm2;列出方程并完成本题解答.
20.(8分)已知关于x的一元二次方程x2+(2m-1)x+m2=0有两个实数根x1和x2.
(1)求实数m的取值范围;(2)当x12-x22=0时,求m的值.(友情提示:若x1,x2是一元二次方程ax2+bx+c=0(a≠0)两根,则有x1+x2=,x1x2=)
21.(10分)(09安徽省)如图6,将正方形沿图中虚线(其中x<y)剪成①②③④四块图形,用这四块图形恰能拼成一个矩形(非正方形).画出拼成的矩形的简图;求的值.
参考答案
1.D 2.D 3.C 4.B 5.D 6.A
7.C提示:设有x人,则x(x-1)=72 8.D 9.-1或2
10.答案不唯一,如(x+1)(x-2)=0,即x2-x-2=0
11. 12.7或8
13.不能 提示:设AD=BC=xm,则AB=(80-2x)m.
由题意得:x(80-2x)=810.△=402-4×405=1600-1620=-20<0.
∴方程无解,故不能围成面积为810m2的矩形场地
14.-1,2, 提示:令x2-2=x(x≤2),解得x1=-1,x2=2.
这两解均符合条件x≤2;再令=x(x>2),解得x=.
但x=不符合条件x>2,∴舍去x=.故所求x的值为-1,2,
15.解:原方程分解因式得(x+2)(x-8)=0,∴x1=-2,x2=8
16.解:依题意得3x2-4x=-3x2+3x-2,即6x2-7x+2=0.
分解因式得(2x-1)(3x-2)=0,所以x=或x=
17.解:(1)x=-1是方程①的一个根,所以1+m-2=0,解得m=1.
方程变为x2-x-2=0,解得,x1=-1,x2=2.
所以方程的另一根为x=2.
(2)b2-4ac=m2+8,因为对于任意实数m,m2≥0,所以m2+8>0,
所以对于任意的实数m,方程①有两个不相等的实数根
18.解:根据题意得:(x-30)(100-2x)=200.整理得:x2-80x+1600=0.
∴(x-40)2=0,x=40(元).于是p=100-2x=20(件).
答:每件商品的售价应定为40元,每天要销售这种商品20件
19.解:(1)20-6x,30-4x,24x2-260x+600;
(2)根据题意,得24x2-260x+600=(1-)×20×30.整理,得6x2-65x+50=0.
解方程,得x1=,x2=10(不合题意,舍去).则2x=,3x=.
答:每个横、竖彩条的宽度分别为cm,cm
20.解:(1)由题意有△=(2m-1)2-4m2≥0,解得m≤.即实数m的取值范围是m≤.
(2)由x12-x22=0得(x1+x2)(x1-x2)=0.若x1+x2=0,即-(2m-1)=0,解得m=.
∵>,∴m=不合题意,舍去.若x1-x2=0,即x1=x2,∴△=0,
由(1)知m=.故当x12-x22=0时,m=
21.解:(1)如图.说明:其它正确拼法可相应赋分.
(2)解法一:由拼图前后的面积相等得:[(x+y)+y]y=(x+y)2.
因为y≠0,整理得:.解得:=(负值不合题意,舍去).
解法二:由拼成的矩形可知:=.以下同解法一.
图1
图2
图3
输入
输出
HYPERLINK "http://" EMBED Equation.DSMT4
是
否
图4
20cm
20cm
30cm
D
C
A
B
图5(2)
图5(1)
30cm
图6
