2020-2021学年人教版八年级数学下册:第18章 平行四边形 复习 学案(习题无答案)
文档属性
| 名称 | 2020-2021学年人教版八年级数学下册:第18章 平行四边形 复习 学案(习题无答案) |
|
|
| 格式 | zip | ||
| 文件大小 | 102.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-04-19 00:00:00 | ||
图片预览

文档简介
平行四边形复习学案
考点透视
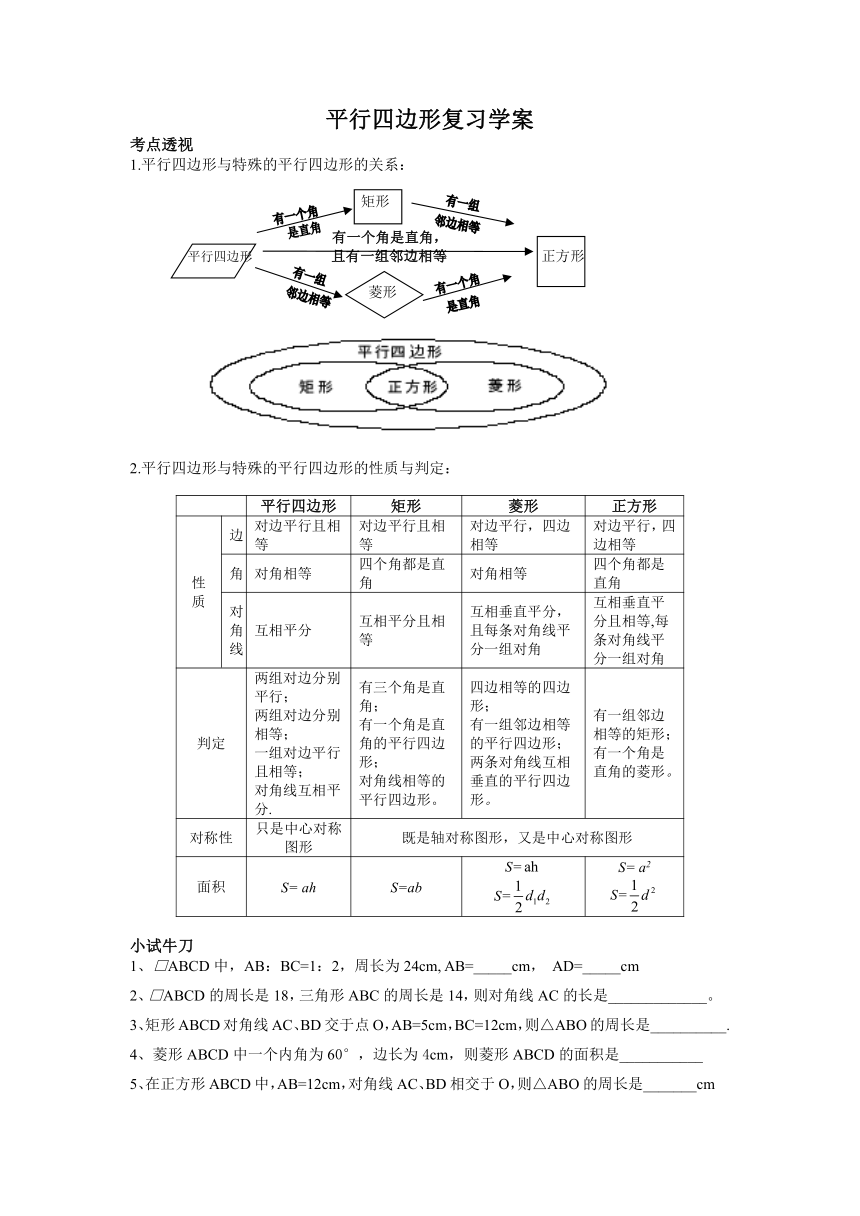
1.平行四边形与特殊的平行四边形的关系:
矩形
有一个角是直角,
平行四边形
且有一组邻边相等
正方形
菱形
2.平行四边形与特殊的平行四边形的性质与判定:
平行四边形
矩形
菱形
正方形
性质
边
对边平行且相等
对边平行且相等
对边平行,四边相等
对边平行,四边相等
角
对角相等
四个角都是直角
对角相等
四个角都是直角
对角线
互相平分
互相平分且相等
互相垂直平分,且每条对角线平分一组对角
互相垂直平分且相等,每条对角线平分一组对角
判定
两组对边分别平行;两组对边分别相等;一组对边平行且相等;对角线互相平分.
有三个角是直角;有一个角是直角的平行四边形;对角线相等的平行四边形。
四边相等的四边形;有一组邻边相等的平行四边形;两条对角线互相垂直的平行四边形。
有一组邻边相等的矩形;有一个角是直角的菱形。
对称性
只是中心对称图形
既是轴对称图形,又是中心对称图形
面积
S=
ah
S=ab
S=S=
S=
a2S=
小试牛刀
1、□ABCD中,AB:BC=1:2,周长为24cm,
AB=_____cm,
AD=_____cm?
2、□ABCD的周长是18,三角形ABC的周长是14,则对角线AC的长是_____________。?
3、矩形ABCD对角线AC、BD交于点O,AB=5cm,BC=12cm,则△ABO的周长是__________.
4、菱形ABCD中一个内角为60°,边长为4cm,则菱形ABCD的面积是___________
5、在正方形ABCD中,AB=12cm,对角线AC、BD相交于O,则△ABO的周长是_______cm?
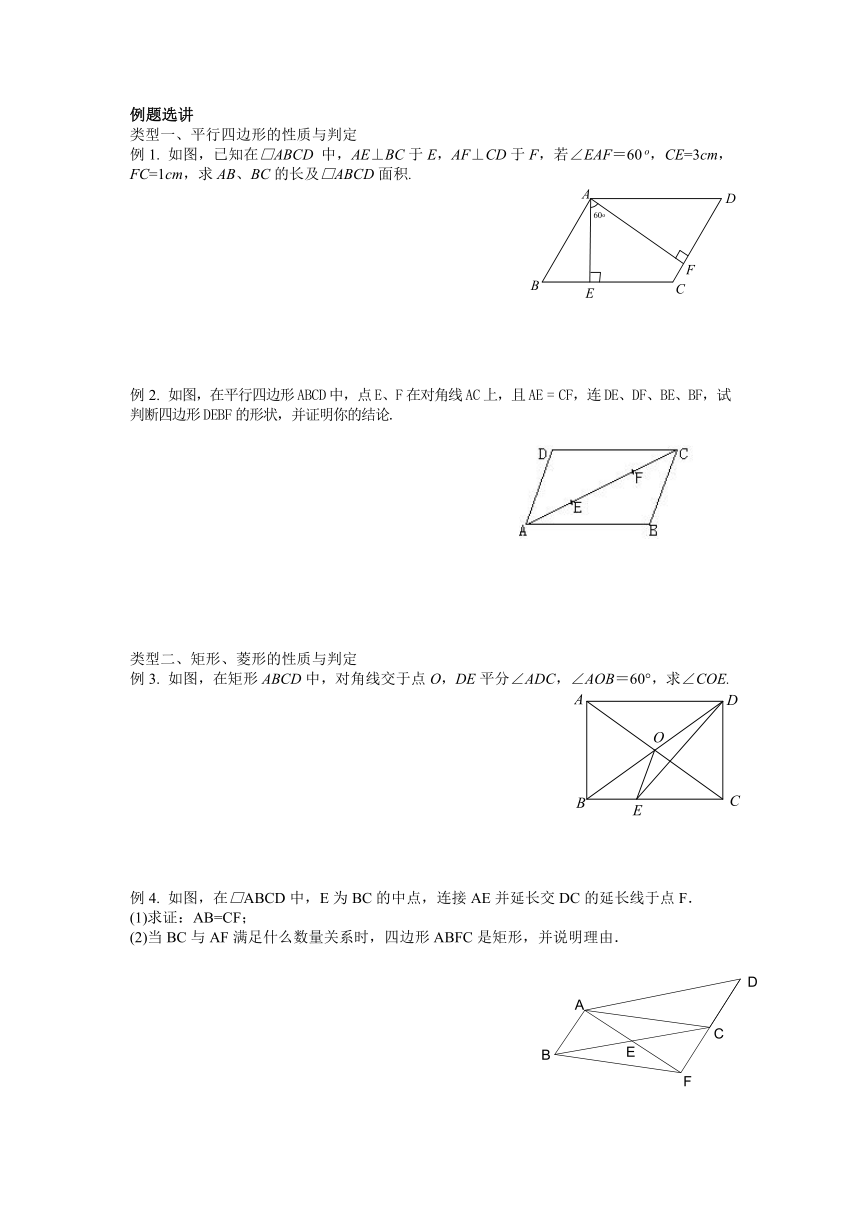
例题选讲
类型一、平行四边形的性质与判定
例1.
如图,已知在□ABCD
中,AE⊥BC于E,AF⊥CD于F,若∠EAF=60
o,CE=3cm,FC=1cm,求AB、BC的长及□ABCD面积.
例2.
如图,在平行四边形ABCD中,点E、F在对角线AC上,且AE
=
CF,连DE、DF、BE、BF,试判断四边形DEBF的形状,并证明你的结论.
类型二、矩形、菱形的性质与判定
例3.
如图,在矩形ABCD中,对角线交于点O,DE平分∠ADC,∠AOB=60°,求∠COE.
例4.
如图,在□ABCD中,E为BC的中点,连接AE并延长交DC的延长线于点F.
(1)求证:AB=CF;
(2)当BC与AF满足什么数量关系时,四边形ABFC是矩形,并说明理由.
例5.
如图,矩形ABCD中的长AB=8,宽AD=5,沿过BD的中点O的直线对折,使B与D点重合,求证:BEDF为菱形,并求折痕EF的长.
例6
.在矩形ABCD中,BC
=
2,AE⊥BD,垂足为E,∠BAE
=
30°,那么ΔECD的面积是多少?
类型三、正方形的性质与判定
例7.
如图,已知E、F分别是正方形ABCD的边BC、CD上的点,AE、AF分别与对角线BD相交于M、N,若∠EAF=50°,则∠CME+∠CNF=
.
例8.
如图,正方形ABCD中,E是CD边上的一点,F为BC延长线上一点,CE=CF.
(1)求证:△BEC≌△DFC;(2)若∠BEC=60°,求∠EFD的度数.
例9.
如图,P是边长为1的正方形ABCD对角线AC上一动点(P与A、C不重合),点E在射线BC上,且PE=PB.
求证:(1)
PE=PD
;
(2)
PE⊥PD;
例10.将一副三角尺如图拼接:含30°角的三角尺(△ABC)的长直角边与含45°角的三角尺(△ACD)的斜边恰好重合.已知AB=2,P是AC上的一个动点.
(1)当点P运动到∠ABC的平分线上时,连接DP,求DP的长;
(2)当点P在运动过程中出现PD=BC时,求此时∠PDA的度数;
(3)当点P运动到什么位置时,以D,P,B,Q为顶点的平行四边形的顶点Q恰好在边BC上?求出此时□DPBQ的面积.
A
B
C
P
D
E
D
A
C
B
考点透视
1.平行四边形与特殊的平行四边形的关系:
矩形
有一个角是直角,
平行四边形
且有一组邻边相等
正方形
菱形
2.平行四边形与特殊的平行四边形的性质与判定:
平行四边形
矩形
菱形
正方形
性质
边
对边平行且相等
对边平行且相等
对边平行,四边相等
对边平行,四边相等
角
对角相等
四个角都是直角
对角相等
四个角都是直角
对角线
互相平分
互相平分且相等
互相垂直平分,且每条对角线平分一组对角
互相垂直平分且相等,每条对角线平分一组对角
判定
两组对边分别平行;两组对边分别相等;一组对边平行且相等;对角线互相平分.
有三个角是直角;有一个角是直角的平行四边形;对角线相等的平行四边形。
四边相等的四边形;有一组邻边相等的平行四边形;两条对角线互相垂直的平行四边形。
有一组邻边相等的矩形;有一个角是直角的菱形。
对称性
只是中心对称图形
既是轴对称图形,又是中心对称图形
面积
S=
ah
S=ab
S=S=
S=
a2S=
小试牛刀
1、□ABCD中,AB:BC=1:2,周长为24cm,
AB=_____cm,
AD=_____cm?
2、□ABCD的周长是18,三角形ABC的周长是14,则对角线AC的长是_____________。?
3、矩形ABCD对角线AC、BD交于点O,AB=5cm,BC=12cm,则△ABO的周长是__________.
4、菱形ABCD中一个内角为60°,边长为4cm,则菱形ABCD的面积是___________
5、在正方形ABCD中,AB=12cm,对角线AC、BD相交于O,则△ABO的周长是_______cm?
例题选讲
类型一、平行四边形的性质与判定
例1.
如图,已知在□ABCD
中,AE⊥BC于E,AF⊥CD于F,若∠EAF=60
o,CE=3cm,FC=1cm,求AB、BC的长及□ABCD面积.
例2.
如图,在平行四边形ABCD中,点E、F在对角线AC上,且AE
=
CF,连DE、DF、BE、BF,试判断四边形DEBF的形状,并证明你的结论.
类型二、矩形、菱形的性质与判定
例3.
如图,在矩形ABCD中,对角线交于点O,DE平分∠ADC,∠AOB=60°,求∠COE.
例4.
如图,在□ABCD中,E为BC的中点,连接AE并延长交DC的延长线于点F.
(1)求证:AB=CF;
(2)当BC与AF满足什么数量关系时,四边形ABFC是矩形,并说明理由.
例5.
如图,矩形ABCD中的长AB=8,宽AD=5,沿过BD的中点O的直线对折,使B与D点重合,求证:BEDF为菱形,并求折痕EF的长.
例6
.在矩形ABCD中,BC
=
2,AE⊥BD,垂足为E,∠BAE
=
30°,那么ΔECD的面积是多少?
类型三、正方形的性质与判定
例7.
如图,已知E、F分别是正方形ABCD的边BC、CD上的点,AE、AF分别与对角线BD相交于M、N,若∠EAF=50°,则∠CME+∠CNF=
.
例8.
如图,正方形ABCD中,E是CD边上的一点,F为BC延长线上一点,CE=CF.
(1)求证:△BEC≌△DFC;(2)若∠BEC=60°,求∠EFD的度数.
例9.
如图,P是边长为1的正方形ABCD对角线AC上一动点(P与A、C不重合),点E在射线BC上,且PE=PB.
求证:(1)
PE=PD
;
(2)
PE⊥PD;
例10.将一副三角尺如图拼接:含30°角的三角尺(△ABC)的长直角边与含45°角的三角尺(△ACD)的斜边恰好重合.已知AB=2,P是AC上的一个动点.
(1)当点P运动到∠ABC的平分线上时,连接DP,求DP的长;
(2)当点P在运动过程中出现PD=BC时,求此时∠PDA的度数;
(3)当点P运动到什么位置时,以D,P,B,Q为顶点的平行四边形的顶点Q恰好在边BC上?求出此时□DPBQ的面积.
A
B
C
P
D
E
D
A
C
B
