2020-2021学年人教版八年级下册数学19.3课题学习 方案选择 同步练习(word含解析)
文档属性
| 名称 | 2020-2021学年人教版八年级下册数学19.3课题学习 方案选择 同步练习(word含解析) |  | |
| 格式 | zip | ||
| 文件大小 | 151.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-04-19 19:33:01 | ||
图片预览


文档简介
19.3课题学习
方案选择
同步练习
一.选择题
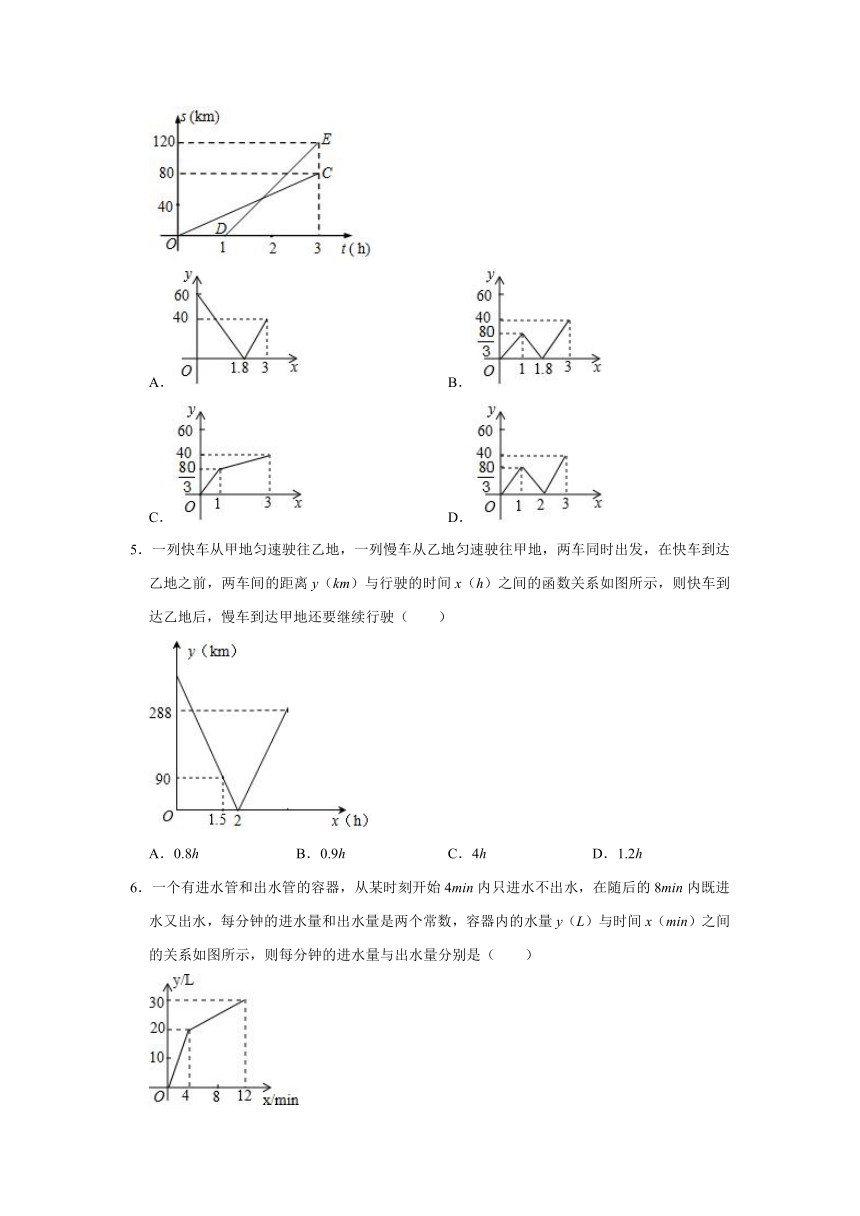
1.如图,若弹簧的总长度y(cm)是关于所挂重物x(kg)的一次函数y=kx+b,则不挂重物时,弹簧的长度是( )
A.5cm
B.8cm
C.9cm
D.10cm
2.如图所示,OA、BA分别表示甲、乙两名学生运动的路程与时间的关系图象,图中S和t分别表示运动路程和时间,根据图象判断快者比慢者每秒多跑( )
A.25m
B.6.25m
C.1.5m
D.1.25m
3.甲、乙两地相距600km,快车走完全程需要10h,慢车走完全程需要15h,两辆车分别从甲、乙两地同时相向而行,从出发到相遇,两车的相距距离y(km)与行驶时间x(h)之间的函数关系式,以及自变量的取值范围( )
A.y=100x+600(0≤x≤6)
B.y=100x﹣600(0≤x≤6)
C.y=﹣100x+600(0≤x≤6)
D.y=﹣100x+600(0≤x<6)
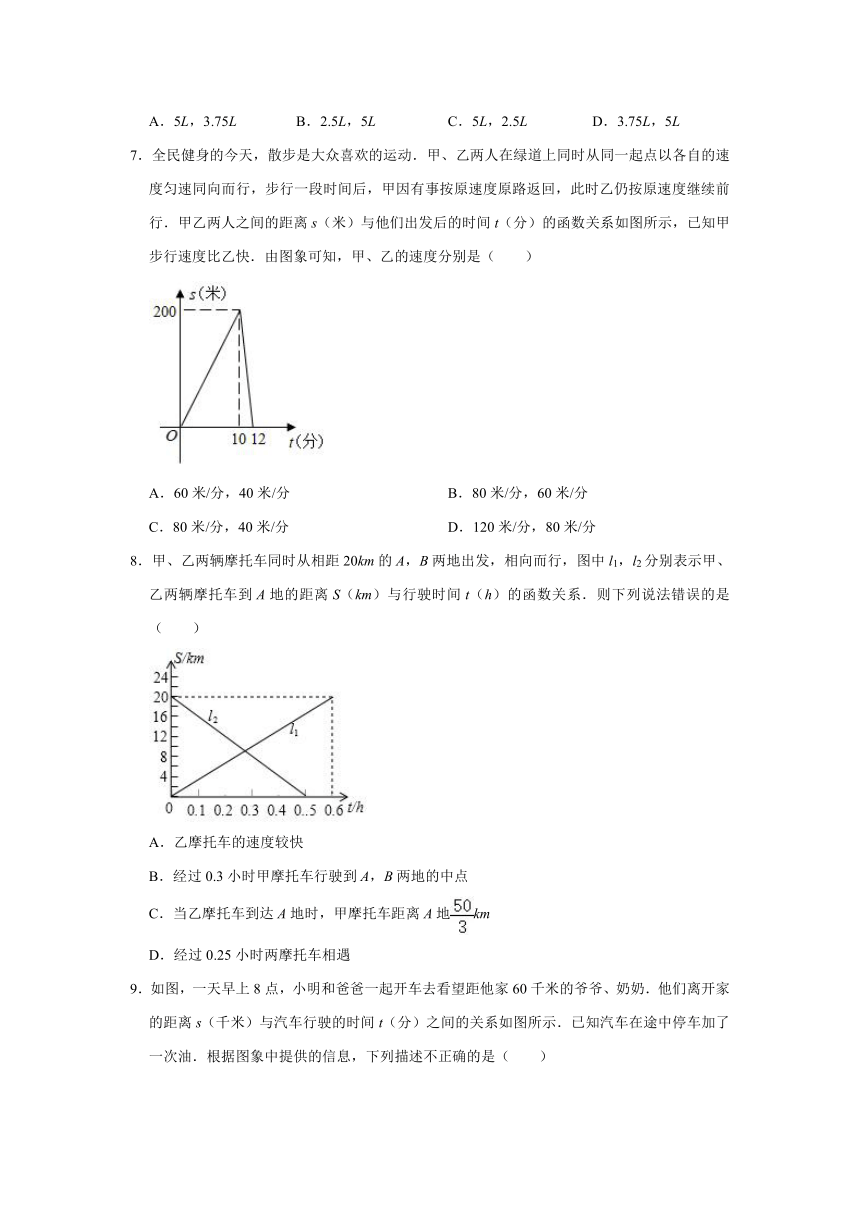
4.已知A,B两地相距120千米,甲、乙两人沿同一条公路从A地出发到B地,乙骑自行车,甲骑摩托车,图中DE,OC分别表示甲、乙离开A地的路程s(单位:千米)与时间t(单位:小时)的函数关系的图象,设在这个过程中,甲、乙两人相距y(单位:千米),则y关于t的函数图象是( )
A.
B.
C.
D.
5.一列快车从甲地匀速驶往乙地,一列慢车从乙地匀速驶往甲地,两车同时出发,在快车到达乙地之前,两车间的距离y(km)与行驶的时间x(h)之间的函数关系如图所示,则快车到达乙地后,慢车到达甲地还要继续行驶( )
A.0.8h
B.0.9h
C.4h
D.1.2h
6.一个有进水管和出水管的容器,从某时刻开始4min内只进水不出水,在随后的8min内既进水又出水,每分钟的进水量和出水量是两个常数,容器内的水量y(L)与时间x(min)之间的关系如图所示,则每分钟的进水量与出水量分别是( )
A.5L,3.75L
B.2.5L,5L
C.5L,2.5L
D.3.75L,5L
7.全民健身的今天,散步是大众喜欢的运动.甲、乙两人在绿道上同时从同一起点以各自的速度匀速同向而行,步行一段时间后,甲因有事按原速度原路返回,此时乙仍按原速度继续前行.甲乙两人之间的距离s(米)与他们出发后的时间t(分)的函数关系如图所示,已知甲步行速度比乙快.由图象可知,甲、乙的速度分别是( )
A.60米/分,40米/分
B.80米/分,60米/分
C.80米/分,40米/分
D.120米/分,80米/分
8.甲、乙两辆摩托车同时从相距20km的A,B两地出发,相向而行,图中l1,l2分别表示甲、乙两辆摩托车到A地的距离S(km)与行驶时间t(h)的函数关系.则下列说法错误的是( )
A.乙摩托车的速度较快
B.经过0.3小时甲摩托车行驶到A,B两地的中点
C.当乙摩托车到达A地时,甲摩托车距离A地km
D.经过0.25小时两摩托车相遇
9.如图,一天早上8点,小明和爸爸一起开车去看望距他家60千米的爷爷、奶奶.他们离开家的距离s(千米)与汽车行驶的时间t(分)之间的关系如图所示.已知汽车在途中停车加了一次油.根据图象中提供的信息,下列描述不正确的是( )
A.加油用了10分钟
B.他们在8点55分到达爷爷家
C.若OA∥BC,则加油后汽车的速度是80千米/时
D.若加油后的速度是90千米/时,则a的值是25
10.甲、乙两车从A城出发前往B城,在整个行驶过程中,汽车离开A城的距离y(km)与行驶时间t(h)的函数图象如图所示,不列说法正确的有( )
①甲车的速度为50km/h
②甲车出发4h时,乙车追上甲车
③乙车用了3h到达B城
④乙车出发后经过1h或3h两车相距50km
A.1个
B.2个
C.3个
D.4个
二.填空题
11.如图是某汽车行驶的路程s(km)与时间t(min)的函数关系图.当16≤t≤30时,s与t的函数关系式为
.
12.声音在空气中的传播速度v(m/s)与温度t(℃)的关系如表:
温度(℃)
0
5
10
15
20
速度v(m/s)
331
336
341
346
351
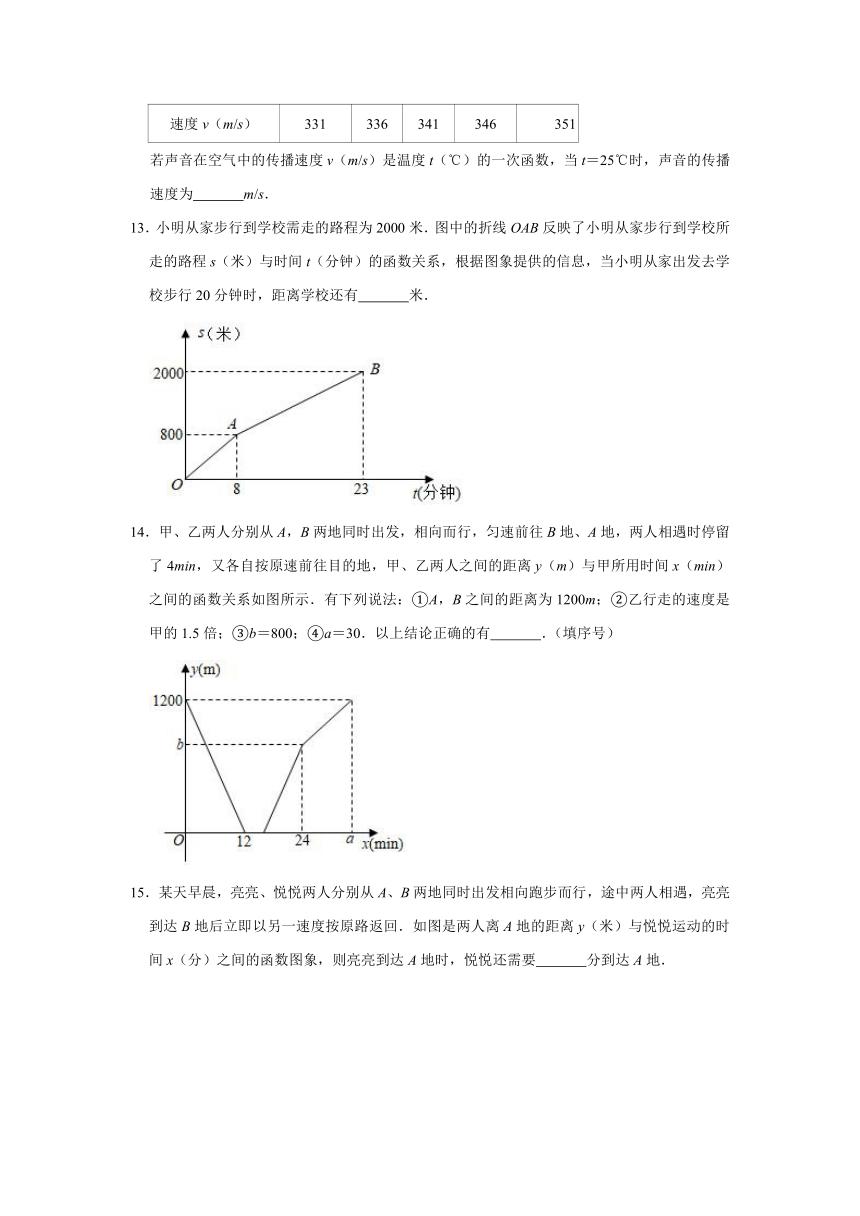
若声音在空气中的传播速度v(m/s)是温度t(℃)的一次函数,当t=25℃时,声音的传播速度为
m/s.
13.小明从家步行到学校需走的路程为2000米.图中的折线OAB反映了小明从家步行到学校所走的路程s(米)与时间t(分钟)的函数关系,根据图象提供的信息,当小明从家出发去学校步行20分钟时,距离学校还有
米.
14.甲、乙两人分别从A,B两地同时出发,相向而行,匀速前往B地、A地,两人相遇时停留了4min,又各自按原速前往目的地,甲、乙两人之间的距离y(m)与甲所用时间x(min)之间的函数关系如图所示.有下列说法:①A,B之间的距离为1200m;②乙行走的速度是甲的1.5倍;③b=800;④a=30.以上结论正确的有
.(填序号)
15.某天早晨,亮亮、悦悦两人分别从A、B两地同时出发相向跑步而行,途中两人相遇,亮亮到达B地后立即以另一速度按原路返回.如图是两人离A地的距离y(米)与悦悦运动的时间x(分)之间的函数图象,则亮亮到达A地时,悦悦还需要
分到达A地.
三.解答题
16.如图,一辆货车和一辆轿车先后从甲地开往乙地,线段OA表示货车离开甲地的距离y(km)与时间x(h)之间的函数关系;折线BCD表示轿车离开甲地的距离y(km)与时间x(h)之间的函数关系,请根据图象解答下列问题:
(1)求线段CD所在直线的函数表达式.
(2)货车出发多长时间两车相遇?此时两车距离乙地多远?
17.已知A,B两地相距200km,甲、乙两辆货车装满货物分别从A,B两地相向而行,图中l1,l2分别表示甲、乙两辆货车离A地的距离s(km)与行驶时间t(h)之间的函数关系.请你根据以上信息,解答下列问题:
(1)分别求出直线l1,l2所对应的函数关系式;
(2)何时甲、乙货车行驶的路程之和超过220km?
18.疫情期间,某企业为了保证能够尽快复工复产,准备为员工采购20000袋医用口罩.因为疫情期间口罩等物资紧缺,无法购买同型号的口罩,经市场调研,准备购买A、B、C三种型号的口罩,这三种型号口罩单价如表所示:
型号
A
B
C
单价(元/袋)
30
35
40
若购买B型口罩的数量是A型的2倍,设购买A型口罩x袋,该企业购买口罩的总费用为y元.
(1)请求出y与x的函数关系式;
(2)已知口罩生产厂家能提供的A型口罩的数量不大于C型口罩的数量,当购买A型口罩多少袋时购买口罩的总费用最少?并求最少总费用.
参考答案
一.选择题
1.解:将(4,10),(20,18)代入y=kx+b,得
,
解得,
∴,
当x=0时,y=8,
∴不挂重物时,弹簧的长度是8cm.
故选:B.
2.解:由图象可得,
快者的速度为:100÷(20﹣4)=100÷16=6.25(m/s),
慢者的速度为:100÷20=5(m/s),
6.25﹣5=1.25(m/s),
即快者比慢者每秒多跑1.25m,
故选:D.
3.解:快车的速度是600÷10=60(km/h),慢车的速度是600÷15=40(km/h),
由行程问题,得y=﹣(60+40)x+600=﹣100x+600(0≤x≤6).
故选:C.
4.解:由题意和图象可得,乙到达B地时甲距A地120km,开始时两人的距离为0;
甲的速度是:120÷(3﹣1)=60km/h,乙的速度是:80÷3=,即乙出发1小时后两人距离为;
设乙出发后被甲追上的时间为xh,则60(x﹣1)=x,得x=1.8,即乙出发后被甲追上的时间为1.8h.
所以符合题意的函数图象只有选项B.
故选:B.
5.解:设当0≤x≤2时,y与x之间的函数关系式为y=kx+b,
将(1.5,90)、(2,0)代入y=kx+b,得:
,解得:,
∴y=﹣180x+360(0≤x≤2),
∴y=180x﹣360(x>2).
当y=288时,有180x﹣360=288,
解得:x=3.6.
当x=0时,y=﹣180x+360=360,
∴甲、乙两地间的距离为360km.
快车的速度为360÷3.6=100(km/h),
慢车的速度为360÷2﹣100=80(km/h),
慢车到达甲地还要继续行驶(360﹣288)÷80=0.9(h).
故选:B.
6.解:由题意可得,
每分钟的进水量为:20÷4=5(L),
每分钟的出水量为:[5×8﹣(30﹣20)]÷8=3.75(L),
故选:A.
7.解:根据题意可知,甲每分钟比乙快:200÷10=20(米),
设乙的速度为x米/分,则甲的速度为(x+20)米/分,
根据题意得:2x+2(x+20)=200,
解得x=40,
40+20=60(米/分),
即甲的速度为60米/分,乙的速度为40米/分,
故选:A.
8.解:由图可得,
甲、乙行驶的路程相等,乙用的时间短,故乙的速度快,故选项A正确;
甲的速度为:20÷0.6=(km/h),则甲行驶0.3h时的路程为:×0.3=10(km),即经过0.3小时甲摩托车行驶到A,B两地的中点,故选项B正确;
当乙摩托车到达A地时,甲摩托车距离A地:×0.5=(km),故选项C正确;
乙的速度为:20÷0.5=40(km/h),则甲、乙相遇时所用的时间是(小时),故选项D错误;
故选:D.
9.解:A、图中加油时间为25至35分钟,共10分钟,故本选项不合题意;
B、他们在8点55分到达爷爷家,说法正确,故本选项不合题意;
C、因为OA∥BC,所以,解得a=,所以加满油以后的速度=千米/小时,说法正确,故本选项不合题意;
D、由题意:,解得a=30,原说法错误,故本选项符合题意;
故选:D.
10.解:①甲车的速度为=50(km/h),故本选项正确;
②甲车出发4h,所走路程是:50×4=200(km),甲车出发4h时,乙走的路程是:×2=200(km),则乙车追上甲车,
故本选项正确;
③乙车到达B城用的时间为:5﹣2=3h,故本选项正确;
④当乙车出发1h时,两车相距:50×3﹣100=50(km),
当乙车出发3h时,两车相距:100×3﹣50×5=50(km),
故本选项正确;
故选:D.
二.填空题
11.解:由函数图象得,当16≤t≤30时,函数图像过点(16,12)和(30,40),
设S与t的函数关系式为:S=kt+b,
将(16,12),(30,40)代入得:
,
解得:,
故当16≤t≤30时,S与t的函数关系式为:S=2t﹣20.
故答案为:S=2t﹣20.
12.解:设声音在空气中的传播速度v(m/s)与温度t(℃)的函数关系式为v=kt+b,
,
即声音在空气中的传播速度v(m/s)与温度t(℃)的函数关系式为v=t+331,
当t=25时,v=25+331=356,
即当t=25℃时,声音的传播速度为356m/s,
故答案为:356.
13.解:设线段AB对应的函数解析式为s=kt+b,
,
解得,
即线段AB对应的函数解析式为s=80t+160,
当t=20时,s=80×20+160=1760,
2000﹣1760=240(米),
即当小明从家出发去学校步行20分钟时,距离学校还有240米,
故答案为:240.
14.解:①当x=0时,y=1200,
∴A、B之间的距离为1200m,结论①正确;
②乙的速度为1200÷(24﹣4)=60(m/min),
甲的速度为1200÷12﹣60=40(m/min),
60÷40=1.5,
∴乙行走的速度是甲的1.5倍,结论②正确;
③b=(60+40)×(24﹣4﹣12)=800,结论③正确;
④a=1200÷40+4=34,结论④错误.
故结论正确的有①②③,
故答案为:①②③.
15.解:根据题意得,
亮亮从A地到B地的速度为:3000÷30=100(米/分),
悦悦的速度为:(3000﹣100×20)÷20=50(米/分),
亮亮返回的速度为:45×50÷(45﹣30)=150(米/分),
亮亮到达A地时,悦悦到达A地还需要的时间为:3000÷50﹣3000÷150﹣30=10(分钟).
故答案为:10
三.解答题
16.解:(1)设线段CD所在直线的函数表达式为:y=kx+b,
由图象可得:甲、乙两地相距300km,轿车比货车晚出发1.2小时,
由题意可得:
,
解得:,
∴线段CD所在直线的函数表达式为:y=110x﹣195(2.5≤x≤4.5);
(3)设OA解析式为:y=mx,
由题意可得:300=5m,
∴m=60,
∴OA解析式为:y=60x,
∴,
解得:,
300﹣234=66(千米),
答:货车出发3.9小时两车相遇,此时两车距离乙地66千米.
17.解:(1)设l1对应的函数关系式为s1=k1t,
∵l1过点(6,200),
∴200=6k,得k1=,
即l1对应的函数关系式为s1=;
设l2对应的函数关系式为s2=k2t+200,
∵l2过点(5,0),
∴0=5k2+200,得k2=﹣40,
即l2所对应的函数关系式为s2=﹣40t+200;
(2)由题意可得,,
解得t>3,
答:3小时后,甲、乙货车行驶的路程之和超过220km.
18.解:(1)由题意可得,
y=30x+35×2x+40(20000﹣x﹣2x)=﹣20x+800000,
即出y与x的函数关系式是y=﹣20x+800000;
(2)∵口罩生产厂家能提供的A型口罩的数量不大于C型口罩的数量,
∴x≤20000﹣x﹣2x,
解得x≤5000,
∵y=﹣20x+800000,
∴y随x的增大而减小,
∴当x=5000时,y取得最小值,此时y=700000,
答:当购买A型口罩5000袋时购买口罩的总费用最少,最少总费用是700000元.
方案选择
同步练习
一.选择题
1.如图,若弹簧的总长度y(cm)是关于所挂重物x(kg)的一次函数y=kx+b,则不挂重物时,弹簧的长度是( )
A.5cm
B.8cm
C.9cm
D.10cm
2.如图所示,OA、BA分别表示甲、乙两名学生运动的路程与时间的关系图象,图中S和t分别表示运动路程和时间,根据图象判断快者比慢者每秒多跑( )
A.25m
B.6.25m
C.1.5m
D.1.25m
3.甲、乙两地相距600km,快车走完全程需要10h,慢车走完全程需要15h,两辆车分别从甲、乙两地同时相向而行,从出发到相遇,两车的相距距离y(km)与行驶时间x(h)之间的函数关系式,以及自变量的取值范围( )
A.y=100x+600(0≤x≤6)
B.y=100x﹣600(0≤x≤6)
C.y=﹣100x+600(0≤x≤6)
D.y=﹣100x+600(0≤x<6)
4.已知A,B两地相距120千米,甲、乙两人沿同一条公路从A地出发到B地,乙骑自行车,甲骑摩托车,图中DE,OC分别表示甲、乙离开A地的路程s(单位:千米)与时间t(单位:小时)的函数关系的图象,设在这个过程中,甲、乙两人相距y(单位:千米),则y关于t的函数图象是( )
A.
B.
C.
D.
5.一列快车从甲地匀速驶往乙地,一列慢车从乙地匀速驶往甲地,两车同时出发,在快车到达乙地之前,两车间的距离y(km)与行驶的时间x(h)之间的函数关系如图所示,则快车到达乙地后,慢车到达甲地还要继续行驶( )
A.0.8h
B.0.9h
C.4h
D.1.2h
6.一个有进水管和出水管的容器,从某时刻开始4min内只进水不出水,在随后的8min内既进水又出水,每分钟的进水量和出水量是两个常数,容器内的水量y(L)与时间x(min)之间的关系如图所示,则每分钟的进水量与出水量分别是( )
A.5L,3.75L
B.2.5L,5L
C.5L,2.5L
D.3.75L,5L
7.全民健身的今天,散步是大众喜欢的运动.甲、乙两人在绿道上同时从同一起点以各自的速度匀速同向而行,步行一段时间后,甲因有事按原速度原路返回,此时乙仍按原速度继续前行.甲乙两人之间的距离s(米)与他们出发后的时间t(分)的函数关系如图所示,已知甲步行速度比乙快.由图象可知,甲、乙的速度分别是( )
A.60米/分,40米/分
B.80米/分,60米/分
C.80米/分,40米/分
D.120米/分,80米/分
8.甲、乙两辆摩托车同时从相距20km的A,B两地出发,相向而行,图中l1,l2分别表示甲、乙两辆摩托车到A地的距离S(km)与行驶时间t(h)的函数关系.则下列说法错误的是( )
A.乙摩托车的速度较快
B.经过0.3小时甲摩托车行驶到A,B两地的中点
C.当乙摩托车到达A地时,甲摩托车距离A地km
D.经过0.25小时两摩托车相遇
9.如图,一天早上8点,小明和爸爸一起开车去看望距他家60千米的爷爷、奶奶.他们离开家的距离s(千米)与汽车行驶的时间t(分)之间的关系如图所示.已知汽车在途中停车加了一次油.根据图象中提供的信息,下列描述不正确的是( )
A.加油用了10分钟
B.他们在8点55分到达爷爷家
C.若OA∥BC,则加油后汽车的速度是80千米/时
D.若加油后的速度是90千米/时,则a的值是25
10.甲、乙两车从A城出发前往B城,在整个行驶过程中,汽车离开A城的距离y(km)与行驶时间t(h)的函数图象如图所示,不列说法正确的有( )
①甲车的速度为50km/h
②甲车出发4h时,乙车追上甲车
③乙车用了3h到达B城
④乙车出发后经过1h或3h两车相距50km
A.1个
B.2个
C.3个
D.4个
二.填空题
11.如图是某汽车行驶的路程s(km)与时间t(min)的函数关系图.当16≤t≤30时,s与t的函数关系式为
.
12.声音在空气中的传播速度v(m/s)与温度t(℃)的关系如表:
温度(℃)
0
5
10
15
20
速度v(m/s)
331
336
341
346
351
若声音在空气中的传播速度v(m/s)是温度t(℃)的一次函数,当t=25℃时,声音的传播速度为
m/s.
13.小明从家步行到学校需走的路程为2000米.图中的折线OAB反映了小明从家步行到学校所走的路程s(米)与时间t(分钟)的函数关系,根据图象提供的信息,当小明从家出发去学校步行20分钟时,距离学校还有
米.
14.甲、乙两人分别从A,B两地同时出发,相向而行,匀速前往B地、A地,两人相遇时停留了4min,又各自按原速前往目的地,甲、乙两人之间的距离y(m)与甲所用时间x(min)之间的函数关系如图所示.有下列说法:①A,B之间的距离为1200m;②乙行走的速度是甲的1.5倍;③b=800;④a=30.以上结论正确的有
.(填序号)
15.某天早晨,亮亮、悦悦两人分别从A、B两地同时出发相向跑步而行,途中两人相遇,亮亮到达B地后立即以另一速度按原路返回.如图是两人离A地的距离y(米)与悦悦运动的时间x(分)之间的函数图象,则亮亮到达A地时,悦悦还需要
分到达A地.
三.解答题
16.如图,一辆货车和一辆轿车先后从甲地开往乙地,线段OA表示货车离开甲地的距离y(km)与时间x(h)之间的函数关系;折线BCD表示轿车离开甲地的距离y(km)与时间x(h)之间的函数关系,请根据图象解答下列问题:
(1)求线段CD所在直线的函数表达式.
(2)货车出发多长时间两车相遇?此时两车距离乙地多远?
17.已知A,B两地相距200km,甲、乙两辆货车装满货物分别从A,B两地相向而行,图中l1,l2分别表示甲、乙两辆货车离A地的距离s(km)与行驶时间t(h)之间的函数关系.请你根据以上信息,解答下列问题:
(1)分别求出直线l1,l2所对应的函数关系式;
(2)何时甲、乙货车行驶的路程之和超过220km?
18.疫情期间,某企业为了保证能够尽快复工复产,准备为员工采购20000袋医用口罩.因为疫情期间口罩等物资紧缺,无法购买同型号的口罩,经市场调研,准备购买A、B、C三种型号的口罩,这三种型号口罩单价如表所示:
型号
A
B
C
单价(元/袋)
30
35
40
若购买B型口罩的数量是A型的2倍,设购买A型口罩x袋,该企业购买口罩的总费用为y元.
(1)请求出y与x的函数关系式;
(2)已知口罩生产厂家能提供的A型口罩的数量不大于C型口罩的数量,当购买A型口罩多少袋时购买口罩的总费用最少?并求最少总费用.
参考答案
一.选择题
1.解:将(4,10),(20,18)代入y=kx+b,得
,
解得,
∴,
当x=0时,y=8,
∴不挂重物时,弹簧的长度是8cm.
故选:B.
2.解:由图象可得,
快者的速度为:100÷(20﹣4)=100÷16=6.25(m/s),
慢者的速度为:100÷20=5(m/s),
6.25﹣5=1.25(m/s),
即快者比慢者每秒多跑1.25m,
故选:D.
3.解:快车的速度是600÷10=60(km/h),慢车的速度是600÷15=40(km/h),
由行程问题,得y=﹣(60+40)x+600=﹣100x+600(0≤x≤6).
故选:C.
4.解:由题意和图象可得,乙到达B地时甲距A地120km,开始时两人的距离为0;
甲的速度是:120÷(3﹣1)=60km/h,乙的速度是:80÷3=,即乙出发1小时后两人距离为;
设乙出发后被甲追上的时间为xh,则60(x﹣1)=x,得x=1.8,即乙出发后被甲追上的时间为1.8h.
所以符合题意的函数图象只有选项B.
故选:B.
5.解:设当0≤x≤2时,y与x之间的函数关系式为y=kx+b,
将(1.5,90)、(2,0)代入y=kx+b,得:
,解得:,
∴y=﹣180x+360(0≤x≤2),
∴y=180x﹣360(x>2).
当y=288时,有180x﹣360=288,
解得:x=3.6.
当x=0时,y=﹣180x+360=360,
∴甲、乙两地间的距离为360km.
快车的速度为360÷3.6=100(km/h),
慢车的速度为360÷2﹣100=80(km/h),
慢车到达甲地还要继续行驶(360﹣288)÷80=0.9(h).
故选:B.
6.解:由题意可得,
每分钟的进水量为:20÷4=5(L),
每分钟的出水量为:[5×8﹣(30﹣20)]÷8=3.75(L),
故选:A.
7.解:根据题意可知,甲每分钟比乙快:200÷10=20(米),
设乙的速度为x米/分,则甲的速度为(x+20)米/分,
根据题意得:2x+2(x+20)=200,
解得x=40,
40+20=60(米/分),
即甲的速度为60米/分,乙的速度为40米/分,
故选:A.
8.解:由图可得,
甲、乙行驶的路程相等,乙用的时间短,故乙的速度快,故选项A正确;
甲的速度为:20÷0.6=(km/h),则甲行驶0.3h时的路程为:×0.3=10(km),即经过0.3小时甲摩托车行驶到A,B两地的中点,故选项B正确;
当乙摩托车到达A地时,甲摩托车距离A地:×0.5=(km),故选项C正确;
乙的速度为:20÷0.5=40(km/h),则甲、乙相遇时所用的时间是(小时),故选项D错误;
故选:D.
9.解:A、图中加油时间为25至35分钟,共10分钟,故本选项不合题意;
B、他们在8点55分到达爷爷家,说法正确,故本选项不合题意;
C、因为OA∥BC,所以,解得a=,所以加满油以后的速度=千米/小时,说法正确,故本选项不合题意;
D、由题意:,解得a=30,原说法错误,故本选项符合题意;
故选:D.
10.解:①甲车的速度为=50(km/h),故本选项正确;
②甲车出发4h,所走路程是:50×4=200(km),甲车出发4h时,乙走的路程是:×2=200(km),则乙车追上甲车,
故本选项正确;
③乙车到达B城用的时间为:5﹣2=3h,故本选项正确;
④当乙车出发1h时,两车相距:50×3﹣100=50(km),
当乙车出发3h时,两车相距:100×3﹣50×5=50(km),
故本选项正确;
故选:D.
二.填空题
11.解:由函数图象得,当16≤t≤30时,函数图像过点(16,12)和(30,40),
设S与t的函数关系式为:S=kt+b,
将(16,12),(30,40)代入得:
,
解得:,
故当16≤t≤30时,S与t的函数关系式为:S=2t﹣20.
故答案为:S=2t﹣20.
12.解:设声音在空气中的传播速度v(m/s)与温度t(℃)的函数关系式为v=kt+b,
,
即声音在空气中的传播速度v(m/s)与温度t(℃)的函数关系式为v=t+331,
当t=25时,v=25+331=356,
即当t=25℃时,声音的传播速度为356m/s,
故答案为:356.
13.解:设线段AB对应的函数解析式为s=kt+b,
,
解得,
即线段AB对应的函数解析式为s=80t+160,
当t=20时,s=80×20+160=1760,
2000﹣1760=240(米),
即当小明从家出发去学校步行20分钟时,距离学校还有240米,
故答案为:240.
14.解:①当x=0时,y=1200,
∴A、B之间的距离为1200m,结论①正确;
②乙的速度为1200÷(24﹣4)=60(m/min),
甲的速度为1200÷12﹣60=40(m/min),
60÷40=1.5,
∴乙行走的速度是甲的1.5倍,结论②正确;
③b=(60+40)×(24﹣4﹣12)=800,结论③正确;
④a=1200÷40+4=34,结论④错误.
故结论正确的有①②③,
故答案为:①②③.
15.解:根据题意得,
亮亮从A地到B地的速度为:3000÷30=100(米/分),
悦悦的速度为:(3000﹣100×20)÷20=50(米/分),
亮亮返回的速度为:45×50÷(45﹣30)=150(米/分),
亮亮到达A地时,悦悦到达A地还需要的时间为:3000÷50﹣3000÷150﹣30=10(分钟).
故答案为:10
三.解答题
16.解:(1)设线段CD所在直线的函数表达式为:y=kx+b,
由图象可得:甲、乙两地相距300km,轿车比货车晚出发1.2小时,
由题意可得:
,
解得:,
∴线段CD所在直线的函数表达式为:y=110x﹣195(2.5≤x≤4.5);
(3)设OA解析式为:y=mx,
由题意可得:300=5m,
∴m=60,
∴OA解析式为:y=60x,
∴,
解得:,
300﹣234=66(千米),
答:货车出发3.9小时两车相遇,此时两车距离乙地66千米.
17.解:(1)设l1对应的函数关系式为s1=k1t,
∵l1过点(6,200),
∴200=6k,得k1=,
即l1对应的函数关系式为s1=;
设l2对应的函数关系式为s2=k2t+200,
∵l2过点(5,0),
∴0=5k2+200,得k2=﹣40,
即l2所对应的函数关系式为s2=﹣40t+200;
(2)由题意可得,,
解得t>3,
答:3小时后,甲、乙货车行驶的路程之和超过220km.
18.解:(1)由题意可得,
y=30x+35×2x+40(20000﹣x﹣2x)=﹣20x+800000,
即出y与x的函数关系式是y=﹣20x+800000;
(2)∵口罩生产厂家能提供的A型口罩的数量不大于C型口罩的数量,
∴x≤20000﹣x﹣2x,
解得x≤5000,
∵y=﹣20x+800000,
∴y随x的增大而减小,
∴当x=5000时,y取得最小值,此时y=700000,
答:当购买A型口罩5000袋时购买口罩的总费用最少,最少总费用是700000元.
