苏科版七年级下册第八章幂的运算全章教学案
文档属性
| 名称 | 苏科版七年级下册第八章幂的运算全章教学案 |
|
|
| 格式 | zip | ||
| 文件大小 | 134.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2012-02-26 00:00:00 | ||
图片预览





文档简介
第八章 幂 的 运 算
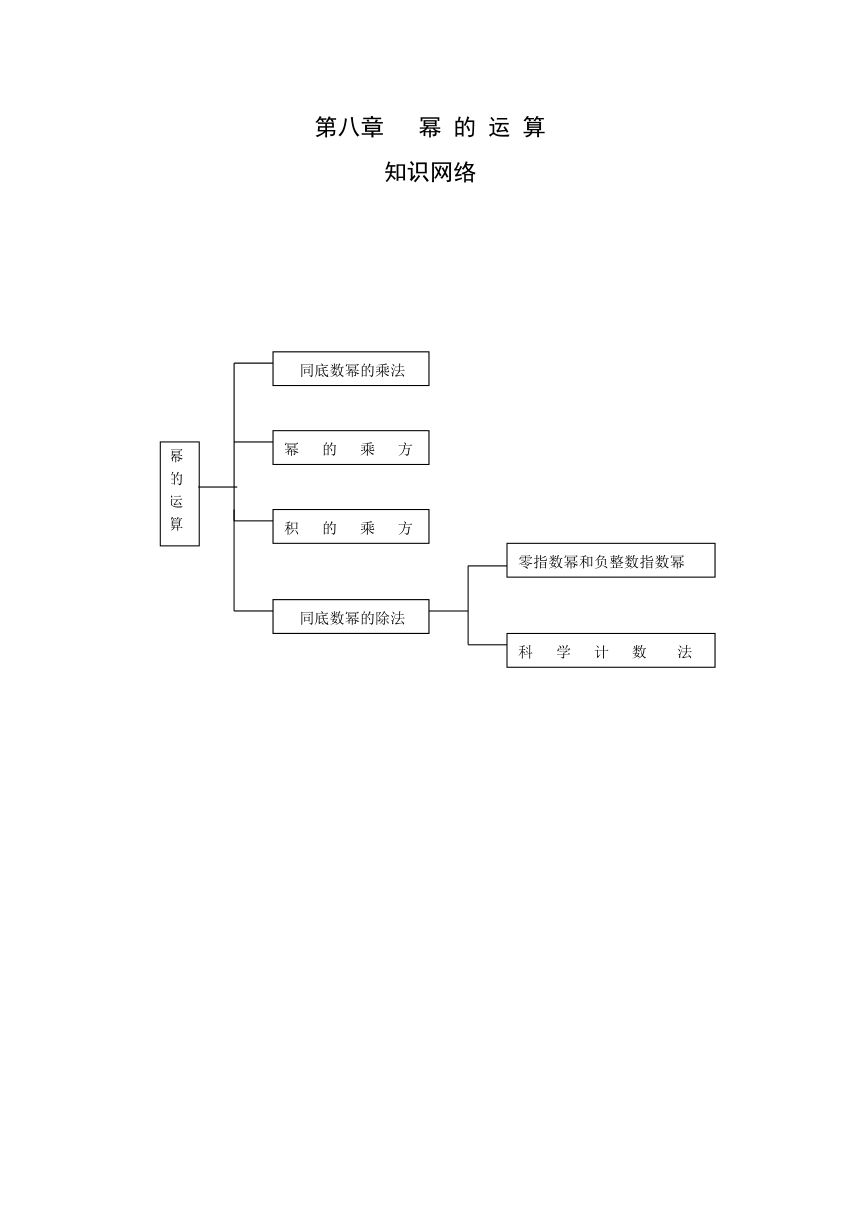
知识网络
8.1同底数幂的乘法——课内练习
『学习目标』
1、能说出同底数幂乘法的运算性质,并会用符号表示。
2、会正确地运用同底数幂乘法的运算性质进行计算,并能说出每一步运算的依据。
『例题精选』
1.计算:
(1); (2); (3); (4)(m是正整数)
思路点拨:关键是判断幂的底数是否相同,利用同底数幂乘法的运算性质进行计算。
一颗卫星绕地球运行的速度是7.9m/s,求这颗卫星运行1h的路程。
思路点拨:这是在新情境中同底数幂乘法性质的运用,关键是转化成数学问题。
已知am=3, an=21, 求am+n的值.
思路点拨:同底数幂乘法性质的逆运用。
『随堂练习』
1.填空:
(1)-23的底数是 ,指数是 ,幂是 .
(2) a5·a3·a2= 10·102·104=
(3)x4·x2n-1= xm·x·xn-2=
(4)(-2) ·(-2)2·(-2)3= (-x)·x3·(-x)2·x5=
(x-y)·(y-x)2·(x-y)3=
(5)若bm·bn·x=bm+n+1 (b≠0且b≠1),则x= .
(6) -x·( )=x4 xm-3· ( )=xm+n
『课堂检测』
1.下列运算错误的是 ( )
A. (-a)(-a)2=-a3 B. –2x2(-3x) = -6x4 C. (-a)3 (-a)2=-a5 D. (-a)3·(-a)3 =a6
2.下列运算错误的是 ( )
A. 3a5-a5=2a5 B. 2m·3n=6m+n C. (a-b)3 (b-a)4=(a-b) D. –a3·(-a)5=a8
3.a14不可以写成 ( )
A.a7+a7 B. a2·a3·a4·a5
C.(-a)(-a)2·(-a)3·(-a)3 D. a5·a9
4.计算:
(1)3x3·x9+x2·x10-2x·x3·x8 (2)32×3×27-3×81×3
8.1同底数幂的乘法——课外作业
『基础过关』
1.3n·(-9)·3n+2的计算结果是 ( )
A.-32n-2 B.-3n+4 C.-32n+4 D.-3n+6
2.计算(x+y-z)3n·(z-x-y)2n·(x-z+y)5n (n为自然数)的结果是( )
A.(x+y-z)10n B.-(x+y-z)10n C. ±(x+y-z)10n D.以上均不正确
『能力训练』
3.计算:
(1) (-1)2m·(-1)2m+1 (2) bn+2·b·b2-bn·b2·b3
(3)b·(-b)2+(-b)·(-b)2 (4)1000×10m×10m-3
(5)2x5·x5+(-x)2·x·(-x)7 (6) (n-m)3·(m-n)2 -(m-n)5
(7)(a-b)·(a-b)4·(b-a) (8)(-x)4+x·(-x)3+2x·(-x)4-(-x)·x4
(9)xm·xm+xp-1·xp-1-xm+1·xm-1 (10) (a+b)(b+a)·(b+a)2+(a+b)2·(-a-b)2
『综合应用』
4.光的速度约为3×105km/s,太阳光照射到地球上大约需要5×102s,地球离太阳大约多远?
5.经济发展和消费需求的增长促进了房地产的销售,2006年前5个月,全国共销售了商品房8.31×107m2,据监测,商品房平均售价为每平方米2.7×103 元,前5个月的商品房销售总额是多少元?
8.2幂的乘方与积的乘方(1)——课内练习
『学习目标』
能说出幂的乘方的运算性质,并会用符号表示;
会运用幂的乘方的运算性质进行运算,并能说出每一步运算的依据。
『例题精选』
1.计算:
(1); (2)(m是正整数); (3); (4)
思路点拨:注意运算结果的符号。
2.计算:
(1); (2)
思路点拨:(1)注意合并同类项;(2)分清幂的性质的运用。
『随堂练习』
1.下面的计算对不对?如果不对,应怎样改正?
(1)(a5)2=a7; (2)a5·a2=a10;(3)(x6)3=x18; (4)(xn+1)2=x2n+1.
2.计算:
(1)(103)3; (2)(x4)3; (3)-(x3)5;
(4)(a2)3·a5; (5)(x2)8·(x4)4; (6)-(xm)5.
『课堂检测』
1.计算:
(1)(-x2)·(x3)2·x; (2)[(x-y)3]4; (3)[(103)2]4.
2.在括号内填入正确数值:
(1)x3·x( )=x6; (2)[x( )]3=x6; (3)x12=x6·x( )=x4·x( )=(x( ))4=x3·x( ).
(4)(x5)( )=x20; (5)x8=x7·x( ).
8.2幂的乘方与积的乘方(1)——课外作业
『基础过关』
1.计算:
(1)(a3)3; (2)(x6)5; (3)-(y7)2;
(4)-(x2)3; (5)(am)3; (6)(x2n)3m.
2.计算:
(1)(x2)3·(x2)2; (2)(y3)4·(y4)3;
(3)(a2)5·(a4)4; (4)(c2)n·cn+1.
3.计算:
(1)(x4)2; (2)x4·x2;
(3)(y5)5; (4)y5·y5.
『能力训练』
4.计算:
(1)(-c3)·(c2)5·c; (2)[(-1)11x2]2.
『综合应用』
5.已知:
8.2幂的乘方与积的乘方(2)——课内练习
『学习目标』
能说出积的乘方的运算性质,并会用符号表示;
会运用积的乘方的运算性质进行运算,并能说出每一步运算的依据。
『例题精选』
1.计算:
(1) (-3x)3; (2) (-5ab)2; (3) (x·y2)2; (4) (-2x·y3z2)4.
思路点拨:注意运算结果的符号。
2.计算:
(1)a3·a4·a+(a2)4+(-2a4)2; (2)2(x3)2·x3-(3x3)3+(5x)2·x7.
思路点拨:计算时,分清幂的性质的运用,不能混用。
『随堂练习』
1.计算:
(1)(ab)6; (2)(2m)3; (3)(-xy)5;
(4)(5ab2)3; (5)(2×102)2; (6)(-3×103)3.
2.计算:
(1)(-2x2y3)3; (2)(-3a3b2c)4.
『课堂检测』
1.下面的计算对不对?如果不对,应怎样改正?
(1)(ab2)3=ab6; (2)(3xy)3=9x3y3; (3)(-2a2)2=-4a4.
2.计算:
(1)(a2)3·(a5)3; (2)(y3)5·(y2)5·(y4)5.
3.计算:
(1) 3(a2)4·(a3)3-(-a)·(a4)4+(-2a4)2·(-a)3·(a2)3.
(2) (x4)2+(x2)4-x·(x2)2·x3-(-x)3·(-x2)2·(-x).
8.2幂的乘方与积的乘方(2)——课外作业
『基础过关』
1.填空:
(1) m4n6=(m2n3)( )=m2n2( ). (2) a4b12=(a2·b6)( )=(ab3)( )=(a2b4)( ).
2.计算:
(1)(a2b)5; (2)(-pq)3; (3)(-a2b3)2;
(4)-(xy2z)4; (5)(-2a2b4c4)4; (6)-(-3xy3)3.
3.计算:
(1)(-2x2y3)+8(x2)2·(-x)2·(-y)3; (2)(-x2)·x3·(-2y)3+(-2xy)2·(-x)3y.
4.计算:
(1)(anb3n)2+(a2b6)n; (2)(-2a)6-(-3a3)2-[-(2a)2]3.
5.计算:
(1) (2) (3)
『能力训练』
6.用简便方法计算
(1) (2)
『综合应用』
7.已知,求m的值
8.3同底数幂的除法(1)——课内练习
『学习目标』
1、能说出同底数幂除法的运算性质,并会用符号表示;
2、会运用同底数幂除法的运算性质进行运算,并能说出每一步运算的依据。
『例题精选』
1.计算:
(1); (2); (3); (4)(m是正整数).
思路点拨:关键是判断幂的底数是否相同,指数又如何处理,不能混用性质。
2.计算:
(1); (2) ; (3).
思路点拨:第(2)题将2a+7看作一个整体,即可用性质。第(3)题注意运算顺序。
3.光的速度约为米/秒,一颗人造地球卫星的速度是米/秒,则光的速度是这颗人造地球卫星速度的多少倍?
『随堂练习』
1.下列运算正确的是( )
A. B. C. D.
2.计算:;。
3.填空:
『课堂检测』
1.下列4个算式
(1) (2 (3) (4)
其中,计算错误的有 ( )
A.4个 B.3个 C.2个 D.1个
2.填空:
(1) ; (2) ;
(3) ,则m= ; (4)() .
3.计算:
(1); (2); (3).
8.3同底数幂的除法(1)——课外作业
『基础过关』
1.下列计算中正确的是( )
A. B. C. D.
2.填空:
(1)( )= (2)( )
(3)( )= (4)( )
3.光的速度约为米/秒,那么光走米要用几秒?
4.计算:
(1) (2)( (3)
(4)( (5)
『能力训练』
5.化简:
『综合应用』
6.若,求n的值.
8.3同底数幂的除法(2)——课内练习
『学习目标』
知道a0=1(a≠0) a-p=1/an(a≠0,n为正整数)的规定,运用这些规定进行转化。
『例题精选』
1.用小数或分数表示下列各数:
(1) (2) (3)3.14
思路点拨:注意负整数指数幂的转化。
2.成立的条件是什么?
思路点拨:注意0指数幂的底数的条件。
3. 将负整数指数化为正整数指数幂:
(1); (2); (3)。
『随堂练习』
1.填空:
(1)当a≠0时,a0=
(2)30÷3-1= ,若(x-2)0=1,则x满足条件
(3)33= 3-3= (-3)3= (-3)-3=
2.选择:
(1)(-0.5)-2等于( )
A.1 B.4 C.-4 D.0.25
(2)(33-3×9)0等于( )
A.1 B.0 C.12 D.无意义
(3)下列算术:①,②(0.0001)0=(1010)0,③10-2=0.001,④中,正确的算术有( )个.
A.0 B.1 C.2 D.3
『课堂检测』
1.填空:
(1)当a≠0,p为正整数时,a-p=
(2)510÷510= 103÷106= 72÷78= (-2)9÷(-2)2=
2.计算:
(1)a8÷a3÷a2 (2)52×5-1-90 (3)5-16×(-2)-3 (4)(52×5-2+50)×5-3
8.3同底数幂的除法(2)——课外作业
『基础过关』
1.在括号内填写各式成立的条件:
(1)x0=1 ( ); (2) (y-2)0=1 ( );
(3)(a-b)0=1 ( ); (4)(|x|-3)0=1 ( );
2.填空:
(1)256b=25·211,则b=__ __ (2)若()x=,则x= (3) ,则x=__ _
3.计算:
(1)a8÷a3÷a2 (2)52×5-1-90
(3)5-16×(-2)-3 (4)(52×5-2+50)×5-3
『能力训练』
4.计算:
(1)(x3)2÷[(x4)3÷(x3)3]3 (2)
(3) (4)
5.在括号内填写各式成立的条件:
(1)x0=1 ( ); (2) (y-2)0=1 ( );
(3)(a-b)0=1 ( ); (4)(|x|-3)0=1 ( );
『综合应用』
6.若a=-0.32,b=-3-2,c= ( )
A.a〈b〈c〈d B. b〈a〈d〈c
C.a〈d〈c〈b D. c〈a〈d〈b
8.3同底数幂的除法(3)——课内练习
『学习目标』
会用科学记数法表示绝对值小于1的数。
『例题精选』
1.人体中的红细胞的直径约为0.0000077米,而流感病毒的直径约为0.00000008米,用科学记数法表示这两个量。
思路点拨:用科学记数法表示数要注意:(1)a的取值范围;(2)n的值的确定。
2.在显微镜下,一种细胞的截面可以近似地看成圆,它的半径约为7.80米,试求这种细胞的截面积。()
『随堂练习』
1.用科学记数法表示下列各数:
(1)360 000 000= ; (2)-2730 000= ;
(3)0.000 00012= ; (4)0.000 1= ;
(5)-0.000 00091= ; (6)0.000 000 007= .
2.写出下列各数的原数:
(1)105= ; (2)10-3= ;
(3)1.2×105= ; (4)2.05×10-5= ;
(5)1.001×10-6= ; (6)3×10-9= .
『课堂检测』
1.填空:若0.000 0003=3×10x,则x= ;
2.实验表明,人体内某种细胞的形状可近似地看作球,它的直径约为0.000 00156m,则这个数用科学记数法表示是 ( )
A.0.156×10-5 B.0.156×105 C.1.56×10-6 D.15.6×10-7
3.计算:
(1) (2) 4-(-2)-2-32÷(-3)0
4.美国旅行者一号太空飞行器在1ns (十亿分之一秒)的时间里能飞行 0.017mm,求飞行器的速度是多少m/s
8.3同底数幂的除法(3)——课外作业
『基础过关』
1.科学家发现一种病毒的直径约为0.000043米,用科学记数法表示为_______________.
2.填空:
(1)= ; (2)= ; (3)= ;
3.0.000000108用科学记数法表示为( )
A. B. C. D.
4.有下列算术:①(0.001)0=1; ②10-3=0.0001;③ 10-5=0.00001; ④(6-3×2)0=1 其中正确的有 ( )
A. 1个 B. 2个 C. 3个 D. 4个
5.纳米是一种长度单位,1纳米=米.已知某种植物花粉的直径约为35000纳米,那么用科学记数法表示为( )
A.米 B.米 C.米 D.米
『能力训练』
6.水珠不断地滴在一块石头上,经过40年,石头上形成了一个深为米的小洞,问平均每个月小洞的深度增加多少(单位:米,用科学记数法表示)?
7.海洋总面积约为,海洋总面积是地球表面积的百分之几?按海洋的海水平均深度计算,求海水的体积。(用科学记数法表示)(地球的表面积约是)
8.某种花粉颗粒的直径约为30 m,多少个这样的花粉颗粒顺次排列能达到1m?(用科学记数法表示)
第八章幂的运算周周清(A卷)
班级 姓名 学号 成绩
一、精心选一选(每题5分,共30分)
1.计算的结果是( )
A. B. C. D.
2、下列运算不正确的是( )
A. B.
C. D.
3.下列计算结果正确的是 ( )
A.(2x)=6x B.(-x)=-x C.(2x)=2x D.[(-x)] =x
4.下列运算正确的是( )
A. B. C. D.
5.已知,则的值为 ( )
A.18 B.8 C.7 D.11
6.下面计算中,正确的是( )
二、细心填一填(每题5分,共30分)
7.计算:;=___________。
8.计算:;。
9、已知3n=a,3m=b,则3m+n+1= ;。
10氢原子中电子和原子核之间的距离为0.00000000529cm,用科学记数法表示这个距离为
cm。
12、若,则x应满足条件___________。
三、专心解一解(共30分)
13.计算:(1) (2)
14.计算:
15.计算:
16.计算:。
17.若,求的值。
18.如果a-4=-3b,求×的值。
19、先化简,再求值,x2 · x2n · (yn+1)2 ,其中,x=-3,y=
四、大胆做一做(共10分)
21.已知x(x-1)-(x2-y)=-2,猜想:-xy的值是多少?
第八章幂的运算周周清(B卷)
班级 姓名 学号 成绩
一、精心选一选(每题5分,共30分)
1.下列运算正确的是( )
A. B. C. D.
2. 我国“神州六号”载人飞船,按预定轨道饶地球70多周,共飞行300多万千米后成功着陆,用科学记数法表示300万千米为( )
A. 3×102千米 B. 3×104千米 C. 3×106 千米 D. 3×1011 千米
3.等于( )
A. B. C. D.
4.2m=3,2n=4,则23m-2n等于( )
A.1 B. C. D.
5.( )
A. B. C. D.
6.计算的结果是( )
A. B. C. D.
二、细心填一填(每题5分,共30分)
1.已知,,,,用“<”连接a、b、c、d为_________________________________
2.计算 ;。
3.填空
4.30÷3-1= ;若(x-2)0=1,则x满足条件
5.256b=25·211,则b=__ __ 若()x=,则x=
6.已知am=3, an=9, 则a3m-2n= .
三、专心解一解(共30分)
1.计算
(1) (-a3)2·(-a2)3 (2) -t3·(-t)4·(-t)5
(3) (p-q)4÷(q-p)3·(p-q)2 (4 ) (-3a)3-(-a)·(-3a)2
2.要使(x-1)0-(x+1)-2有意义,x的取值应满足什么条件?
3.已知x3=m,x5=n,用含有m,n的代数式表示x14。
4、水珠不断地滴在一块石头上,经过40年,石头上形成了一个深为米的小洞,问
平均每个月小洞的深度增加多少(单位:米,用科学记数法表示)?
5.设A=,B=,C=,试比较A、B、C的大小关系。
6.已知,求的值。
四、大胆做一做(共10分)
1.求的末位数字。
2.若x=,y=3+,请用x的代数式表示y.
幂 的 运 算
同底数幂的乘法
幂 的 乘 方
积 的 乘 方
同底数幂的除法
零指数幂和负整数指数幂
科 学 计 数 法
知识网络
8.1同底数幂的乘法——课内练习
『学习目标』
1、能说出同底数幂乘法的运算性质,并会用符号表示。
2、会正确地运用同底数幂乘法的运算性质进行计算,并能说出每一步运算的依据。
『例题精选』
1.计算:
(1); (2); (3); (4)(m是正整数)
思路点拨:关键是判断幂的底数是否相同,利用同底数幂乘法的运算性质进行计算。
一颗卫星绕地球运行的速度是7.9m/s,求这颗卫星运行1h的路程。
思路点拨:这是在新情境中同底数幂乘法性质的运用,关键是转化成数学问题。
已知am=3, an=21, 求am+n的值.
思路点拨:同底数幂乘法性质的逆运用。
『随堂练习』
1.填空:
(1)-23的底数是 ,指数是 ,幂是 .
(2) a5·a3·a2= 10·102·104=
(3)x4·x2n-1= xm·x·xn-2=
(4)(-2) ·(-2)2·(-2)3= (-x)·x3·(-x)2·x5=
(x-y)·(y-x)2·(x-y)3=
(5)若bm·bn·x=bm+n+1 (b≠0且b≠1),则x= .
(6) -x·( )=x4 xm-3· ( )=xm+n
『课堂检测』
1.下列运算错误的是 ( )
A. (-a)(-a)2=-a3 B. –2x2(-3x) = -6x4 C. (-a)3 (-a)2=-a5 D. (-a)3·(-a)3 =a6
2.下列运算错误的是 ( )
A. 3a5-a5=2a5 B. 2m·3n=6m+n C. (a-b)3 (b-a)4=(a-b) D. –a3·(-a)5=a8
3.a14不可以写成 ( )
A.a7+a7 B. a2·a3·a4·a5
C.(-a)(-a)2·(-a)3·(-a)3 D. a5·a9
4.计算:
(1)3x3·x9+x2·x10-2x·x3·x8 (2)32×3×27-3×81×3
8.1同底数幂的乘法——课外作业
『基础过关』
1.3n·(-9)·3n+2的计算结果是 ( )
A.-32n-2 B.-3n+4 C.-32n+4 D.-3n+6
2.计算(x+y-z)3n·(z-x-y)2n·(x-z+y)5n (n为自然数)的结果是( )
A.(x+y-z)10n B.-(x+y-z)10n C. ±(x+y-z)10n D.以上均不正确
『能力训练』
3.计算:
(1) (-1)2m·(-1)2m+1 (2) bn+2·b·b2-bn·b2·b3
(3)b·(-b)2+(-b)·(-b)2 (4)1000×10m×10m-3
(5)2x5·x5+(-x)2·x·(-x)7 (6) (n-m)3·(m-n)2 -(m-n)5
(7)(a-b)·(a-b)4·(b-a) (8)(-x)4+x·(-x)3+2x·(-x)4-(-x)·x4
(9)xm·xm+xp-1·xp-1-xm+1·xm-1 (10) (a+b)(b+a)·(b+a)2+(a+b)2·(-a-b)2
『综合应用』
4.光的速度约为3×105km/s,太阳光照射到地球上大约需要5×102s,地球离太阳大约多远?
5.经济发展和消费需求的增长促进了房地产的销售,2006年前5个月,全国共销售了商品房8.31×107m2,据监测,商品房平均售价为每平方米2.7×103 元,前5个月的商品房销售总额是多少元?
8.2幂的乘方与积的乘方(1)——课内练习
『学习目标』
能说出幂的乘方的运算性质,并会用符号表示;
会运用幂的乘方的运算性质进行运算,并能说出每一步运算的依据。
『例题精选』
1.计算:
(1); (2)(m是正整数); (3); (4)
思路点拨:注意运算结果的符号。
2.计算:
(1); (2)
思路点拨:(1)注意合并同类项;(2)分清幂的性质的运用。
『随堂练习』
1.下面的计算对不对?如果不对,应怎样改正?
(1)(a5)2=a7; (2)a5·a2=a10;(3)(x6)3=x18; (4)(xn+1)2=x2n+1.
2.计算:
(1)(103)3; (2)(x4)3; (3)-(x3)5;
(4)(a2)3·a5; (5)(x2)8·(x4)4; (6)-(xm)5.
『课堂检测』
1.计算:
(1)(-x2)·(x3)2·x; (2)[(x-y)3]4; (3)[(103)2]4.
2.在括号内填入正确数值:
(1)x3·x( )=x6; (2)[x( )]3=x6; (3)x12=x6·x( )=x4·x( )=(x( ))4=x3·x( ).
(4)(x5)( )=x20; (5)x8=x7·x( ).
8.2幂的乘方与积的乘方(1)——课外作业
『基础过关』
1.计算:
(1)(a3)3; (2)(x6)5; (3)-(y7)2;
(4)-(x2)3; (5)(am)3; (6)(x2n)3m.
2.计算:
(1)(x2)3·(x2)2; (2)(y3)4·(y4)3;
(3)(a2)5·(a4)4; (4)(c2)n·cn+1.
3.计算:
(1)(x4)2; (2)x4·x2;
(3)(y5)5; (4)y5·y5.
『能力训练』
4.计算:
(1)(-c3)·(c2)5·c; (2)[(-1)11x2]2.
『综合应用』
5.已知:
8.2幂的乘方与积的乘方(2)——课内练习
『学习目标』
能说出积的乘方的运算性质,并会用符号表示;
会运用积的乘方的运算性质进行运算,并能说出每一步运算的依据。
『例题精选』
1.计算:
(1) (-3x)3; (2) (-5ab)2; (3) (x·y2)2; (4) (-2x·y3z2)4.
思路点拨:注意运算结果的符号。
2.计算:
(1)a3·a4·a+(a2)4+(-2a4)2; (2)2(x3)2·x3-(3x3)3+(5x)2·x7.
思路点拨:计算时,分清幂的性质的运用,不能混用。
『随堂练习』
1.计算:
(1)(ab)6; (2)(2m)3; (3)(-xy)5;
(4)(5ab2)3; (5)(2×102)2; (6)(-3×103)3.
2.计算:
(1)(-2x2y3)3; (2)(-3a3b2c)4.
『课堂检测』
1.下面的计算对不对?如果不对,应怎样改正?
(1)(ab2)3=ab6; (2)(3xy)3=9x3y3; (3)(-2a2)2=-4a4.
2.计算:
(1)(a2)3·(a5)3; (2)(y3)5·(y2)5·(y4)5.
3.计算:
(1) 3(a2)4·(a3)3-(-a)·(a4)4+(-2a4)2·(-a)3·(a2)3.
(2) (x4)2+(x2)4-x·(x2)2·x3-(-x)3·(-x2)2·(-x).
8.2幂的乘方与积的乘方(2)——课外作业
『基础过关』
1.填空:
(1) m4n6=(m2n3)( )=m2n2( ). (2) a4b12=(a2·b6)( )=(ab3)( )=(a2b4)( ).
2.计算:
(1)(a2b)5; (2)(-pq)3; (3)(-a2b3)2;
(4)-(xy2z)4; (5)(-2a2b4c4)4; (6)-(-3xy3)3.
3.计算:
(1)(-2x2y3)+8(x2)2·(-x)2·(-y)3; (2)(-x2)·x3·(-2y)3+(-2xy)2·(-x)3y.
4.计算:
(1)(anb3n)2+(a2b6)n; (2)(-2a)6-(-3a3)2-[-(2a)2]3.
5.计算:
(1) (2) (3)
『能力训练』
6.用简便方法计算
(1) (2)
『综合应用』
7.已知,求m的值
8.3同底数幂的除法(1)——课内练习
『学习目标』
1、能说出同底数幂除法的运算性质,并会用符号表示;
2、会运用同底数幂除法的运算性质进行运算,并能说出每一步运算的依据。
『例题精选』
1.计算:
(1); (2); (3); (4)(m是正整数).
思路点拨:关键是判断幂的底数是否相同,指数又如何处理,不能混用性质。
2.计算:
(1); (2) ; (3).
思路点拨:第(2)题将2a+7看作一个整体,即可用性质。第(3)题注意运算顺序。
3.光的速度约为米/秒,一颗人造地球卫星的速度是米/秒,则光的速度是这颗人造地球卫星速度的多少倍?
『随堂练习』
1.下列运算正确的是( )
A. B. C. D.
2.计算:;。
3.填空:
『课堂检测』
1.下列4个算式
(1) (2 (3) (4)
其中,计算错误的有 ( )
A.4个 B.3个 C.2个 D.1个
2.填空:
(1) ; (2) ;
(3) ,则m= ; (4)() .
3.计算:
(1); (2); (3).
8.3同底数幂的除法(1)——课外作业
『基础过关』
1.下列计算中正确的是( )
A. B. C. D.
2.填空:
(1)( )= (2)( )
(3)( )= (4)( )
3.光的速度约为米/秒,那么光走米要用几秒?
4.计算:
(1) (2)( (3)
(4)( (5)
『能力训练』
5.化简:
『综合应用』
6.若,求n的值.
8.3同底数幂的除法(2)——课内练习
『学习目标』
知道a0=1(a≠0) a-p=1/an(a≠0,n为正整数)的规定,运用这些规定进行转化。
『例题精选』
1.用小数或分数表示下列各数:
(1) (2) (3)3.14
思路点拨:注意负整数指数幂的转化。
2.成立的条件是什么?
思路点拨:注意0指数幂的底数的条件。
3. 将负整数指数化为正整数指数幂:
(1); (2); (3)。
『随堂练习』
1.填空:
(1)当a≠0时,a0=
(2)30÷3-1= ,若(x-2)0=1,则x满足条件
(3)33= 3-3= (-3)3= (-3)-3=
2.选择:
(1)(-0.5)-2等于( )
A.1 B.4 C.-4 D.0.25
(2)(33-3×9)0等于( )
A.1 B.0 C.12 D.无意义
(3)下列算术:①,②(0.0001)0=(1010)0,③10-2=0.001,④中,正确的算术有( )个.
A.0 B.1 C.2 D.3
『课堂检测』
1.填空:
(1)当a≠0,p为正整数时,a-p=
(2)510÷510= 103÷106= 72÷78= (-2)9÷(-2)2=
2.计算:
(1)a8÷a3÷a2 (2)52×5-1-90 (3)5-16×(-2)-3 (4)(52×5-2+50)×5-3
8.3同底数幂的除法(2)——课外作业
『基础过关』
1.在括号内填写各式成立的条件:
(1)x0=1 ( ); (2) (y-2)0=1 ( );
(3)(a-b)0=1 ( ); (4)(|x|-3)0=1 ( );
2.填空:
(1)256b=25·211,则b=__ __ (2)若()x=,则x= (3) ,则x=__ _
3.计算:
(1)a8÷a3÷a2 (2)52×5-1-90
(3)5-16×(-2)-3 (4)(52×5-2+50)×5-3
『能力训练』
4.计算:
(1)(x3)2÷[(x4)3÷(x3)3]3 (2)
(3) (4)
5.在括号内填写各式成立的条件:
(1)x0=1 ( ); (2) (y-2)0=1 ( );
(3)(a-b)0=1 ( ); (4)(|x|-3)0=1 ( );
『综合应用』
6.若a=-0.32,b=-3-2,c= ( )
A.a〈b〈c〈d B. b〈a〈d〈c
C.a〈d〈c〈b D. c〈a〈d〈b
8.3同底数幂的除法(3)——课内练习
『学习目标』
会用科学记数法表示绝对值小于1的数。
『例题精选』
1.人体中的红细胞的直径约为0.0000077米,而流感病毒的直径约为0.00000008米,用科学记数法表示这两个量。
思路点拨:用科学记数法表示数要注意:(1)a的取值范围;(2)n的值的确定。
2.在显微镜下,一种细胞的截面可以近似地看成圆,它的半径约为7.80米,试求这种细胞的截面积。()
『随堂练习』
1.用科学记数法表示下列各数:
(1)360 000 000= ; (2)-2730 000= ;
(3)0.000 00012= ; (4)0.000 1= ;
(5)-0.000 00091= ; (6)0.000 000 007= .
2.写出下列各数的原数:
(1)105= ; (2)10-3= ;
(3)1.2×105= ; (4)2.05×10-5= ;
(5)1.001×10-6= ; (6)3×10-9= .
『课堂检测』
1.填空:若0.000 0003=3×10x,则x= ;
2.实验表明,人体内某种细胞的形状可近似地看作球,它的直径约为0.000 00156m,则这个数用科学记数法表示是 ( )
A.0.156×10-5 B.0.156×105 C.1.56×10-6 D.15.6×10-7
3.计算:
(1) (2) 4-(-2)-2-32÷(-3)0
4.美国旅行者一号太空飞行器在1ns (十亿分之一秒)的时间里能飞行 0.017mm,求飞行器的速度是多少m/s
8.3同底数幂的除法(3)——课外作业
『基础过关』
1.科学家发现一种病毒的直径约为0.000043米,用科学记数法表示为_______________.
2.填空:
(1)= ; (2)= ; (3)= ;
3.0.000000108用科学记数法表示为( )
A. B. C. D.
4.有下列算术:①(0.001)0=1; ②10-3=0.0001;③ 10-5=0.00001; ④(6-3×2)0=1 其中正确的有 ( )
A. 1个 B. 2个 C. 3个 D. 4个
5.纳米是一种长度单位,1纳米=米.已知某种植物花粉的直径约为35000纳米,那么用科学记数法表示为( )
A.米 B.米 C.米 D.米
『能力训练』
6.水珠不断地滴在一块石头上,经过40年,石头上形成了一个深为米的小洞,问平均每个月小洞的深度增加多少(单位:米,用科学记数法表示)?
7.海洋总面积约为,海洋总面积是地球表面积的百分之几?按海洋的海水平均深度计算,求海水的体积。(用科学记数法表示)(地球的表面积约是)
8.某种花粉颗粒的直径约为30 m,多少个这样的花粉颗粒顺次排列能达到1m?(用科学记数法表示)
第八章幂的运算周周清(A卷)
班级 姓名 学号 成绩
一、精心选一选(每题5分,共30分)
1.计算的结果是( )
A. B. C. D.
2、下列运算不正确的是( )
A. B.
C. D.
3.下列计算结果正确的是 ( )
A.(2x)=6x B.(-x)=-x C.(2x)=2x D.[(-x)] =x
4.下列运算正确的是( )
A. B. C. D.
5.已知,则的值为 ( )
A.18 B.8 C.7 D.11
6.下面计算中,正确的是( )
二、细心填一填(每题5分,共30分)
7.计算:;=___________。
8.计算:;。
9、已知3n=a,3m=b,则3m+n+1= ;。
10氢原子中电子和原子核之间的距离为0.00000000529cm,用科学记数法表示这个距离为
cm。
12、若,则x应满足条件___________。
三、专心解一解(共30分)
13.计算:(1) (2)
14.计算:
15.计算:
16.计算:。
17.若,求的值。
18.如果a-4=-3b,求×的值。
19、先化简,再求值,x2 · x2n · (yn+1)2 ,其中,x=-3,y=
四、大胆做一做(共10分)
21.已知x(x-1)-(x2-y)=-2,猜想:-xy的值是多少?
第八章幂的运算周周清(B卷)
班级 姓名 学号 成绩
一、精心选一选(每题5分,共30分)
1.下列运算正确的是( )
A. B. C. D.
2. 我国“神州六号”载人飞船,按预定轨道饶地球70多周,共飞行300多万千米后成功着陆,用科学记数法表示300万千米为( )
A. 3×102千米 B. 3×104千米 C. 3×106 千米 D. 3×1011 千米
3.等于( )
A. B. C. D.
4.2m=3,2n=4,则23m-2n等于( )
A.1 B. C. D.
5.( )
A. B. C. D.
6.计算的结果是( )
A. B. C. D.
二、细心填一填(每题5分,共30分)
1.已知,,,,用“<”连接a、b、c、d为_________________________________
2.计算 ;。
3.填空
4.30÷3-1= ;若(x-2)0=1,则x满足条件
5.256b=25·211,则b=__ __ 若()x=,则x=
6.已知am=3, an=9, 则a3m-2n= .
三、专心解一解(共30分)
1.计算
(1) (-a3)2·(-a2)3 (2) -t3·(-t)4·(-t)5
(3) (p-q)4÷(q-p)3·(p-q)2 (4 ) (-3a)3-(-a)·(-3a)2
2.要使(x-1)0-(x+1)-2有意义,x的取值应满足什么条件?
3.已知x3=m,x5=n,用含有m,n的代数式表示x14。
4、水珠不断地滴在一块石头上,经过40年,石头上形成了一个深为米的小洞,问
平均每个月小洞的深度增加多少(单位:米,用科学记数法表示)?
5.设A=,B=,C=,试比较A、B、C的大小关系。
6.已知,求的值。
四、大胆做一做(共10分)
1.求的末位数字。
2.若x=,y=3+,请用x的代数式表示y.
幂 的 运 算
同底数幂的乘法
幂 的 乘 方
积 的 乘 方
同底数幂的除法
零指数幂和负整数指数幂
科 学 计 数 法
同课章节目录
- 第7章 平面图形的认识(二)
- 7.1 探索直线平行的条件
- 7.2 探索平行线的性质
- 7.3 图形的平移
- 7.4 认识三角形
- 7.5 多边形的内角和与外角和
- 第8章 幂的运算
- 8.1 同底数幂的乘法
- 8.2 幂的乘方与积的乘方
- 8.3 同底数幂的除法
- 第9章 整式乘法与因式分解
- 9.1 单项式乘单项式
- 9.2 单项式乘多项式
- 9.3 多项式乘多项式
- 9.4 乘法公式
- 9.5 多项式的因式分解
- 第10章 二元一次方程组
- 10.1 二元一次方程
- 10.2 二元一次方程组
- 10.3 解二元一次方程组
- 10.4 三元一次方程组
- 10.5 用二元一次方程解决问题
- 第11章 一元一次不等式
- 11.1 生活中的不等式
- 11.2 不等式的解集
- 11.3 不等式的性质
- 11.4 解一元一次不等式
- 11.5 用一元一次不等式解决问题
- 11.6 一元一次不等式组
- 第12章 证明
- 12.1 定义与命题
- 12.2 证明
- 12.3 互逆命题
