苏科版七年级上册第三章 《用字母表示数》全章教案
文档属性
| 名称 | 苏科版七年级上册第三章 《用字母表示数》全章教案 |
|
|
| 格式 | zip | ||
| 文件大小 | 54.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2012-02-26 00:00:00 | ||
图片预览





文档简介
第三章 用字母表示数
第1课时 字母表示数
目的与要求 领会用字母表示数是数量关系的一种抽象化,是代数的一个重要特点。
知识与技能 用字母表示数,了解抽象概括的思维方法。
情感、态度与价值观 初步认识辩证唯物主义观点--从特殊到一般。
教学过程
一、情境的引入
1、从日历中,观察后填写下表:
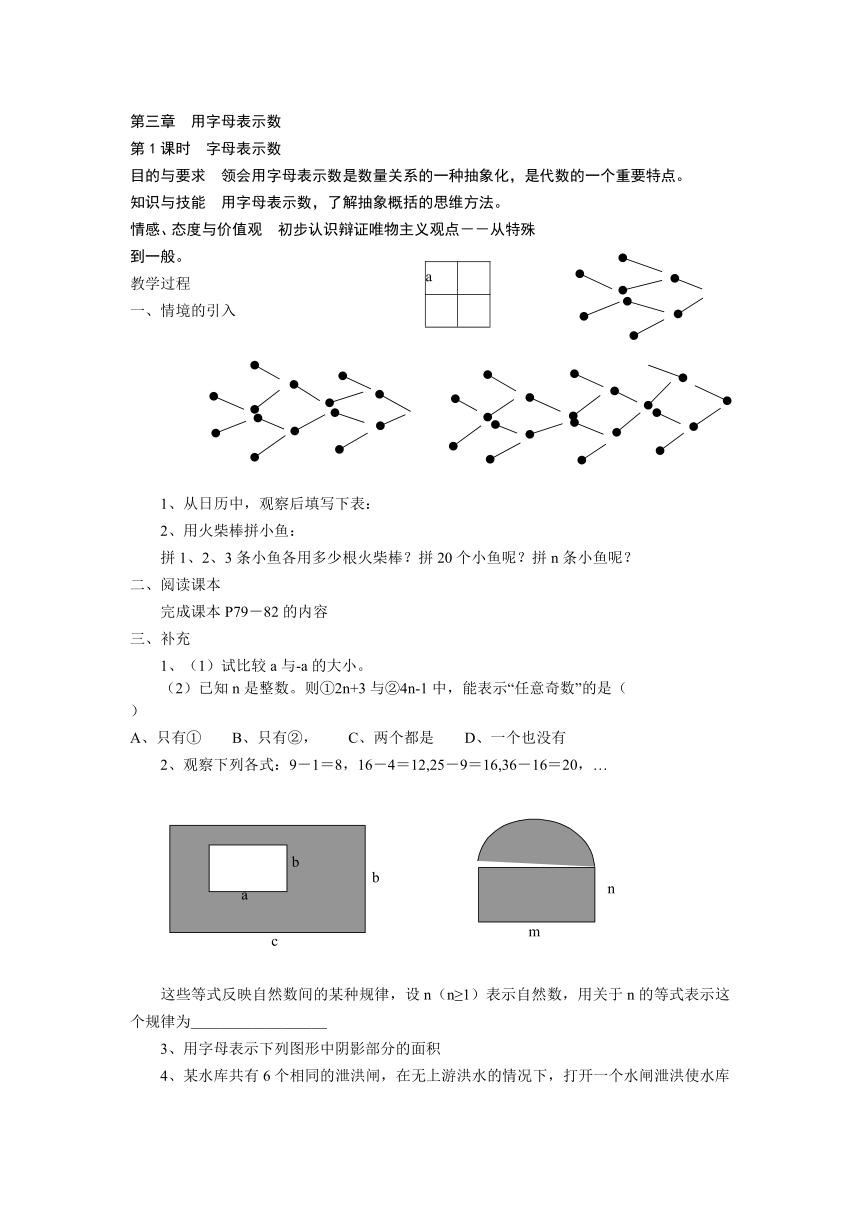
2、用火柴棒拼小鱼:
拼1、2、3条小鱼各用多少根火柴棒?拼20个小鱼呢?拼n条小鱼呢?
二、阅读课本
完成课本P79-82的内容
三、补充
1、(1)试比较a与-a的大小。
(2)已知n是整数。则①2n+3与②4n-1中,能表示“任意奇数”的是(
a
)
A、只有① B、只有②, C、两个都是 D、一个也没有
2、观察下列各式:9-1=8,16-4=12,25-9=16,36-16=20,…
这些等式反映自然数间的某种规律,设n(n≥1)表示自然数,用关于n的等式表示这个规律为_________
3、用字母表示下列图形中阴影部分的面积
4、某水库共有6个相同的泄洪闸,在无上游洪水的情况下,打开一个水闸泄洪使水库水位以a米/时匀速下降,汛期上游的洪水在未开泄洪闸的情况下使水库水位以b米/时匀速上升,当水库水位超警戒线h米时开始泄洪,如果打开n个水闸泄洪x小时,那么此时相对于警戒线的水面高度应为________。
解答:h+bx-nax
四、课堂练习
练习纸
五、课堂小结
这节课我们学会了什么?
六、课堂作业
见作业本
七、课后反馈
第2、3课时 代数式(第1课时代数式及有关概念,第2课时列代数式)
目的与要求 了解代数式的意义,知道一个代数式所表示的数量关系,会说出单项式的系数。
知识与技能 通过同一个代数式常常可以表示不同实际问题的数量关系,培养语言表达能力与发散思维能力。
情感、态度与价值观 培养学生实事求是、严谨的科学态度。
教学过程
一、情境引入
(1)求边长为a的正方形的周长和面积。
(2)求长a,宽为b的长方形的周长、面积。
(3)当路程为s,时间为t时,其速度为多少?
(4)长为a,宽为b,高为c的长方体的体积是多少?
二、新授
像上面的 的式子,都是由数、字母和运算符号构成的,称它们为代数式。(algebraic expression).单独的一个数和一个字母也是代数式。
例1、有下列各式
其中哪些是代数式?
像 ,abc都是数与字母的积,这样的代数式叫做单项式(monomial),单独一个数或一个字母也叫做单项式。单项式前面的数字因数叫做它的系数(coefficient)
单项式中所有字母的指数的和叫做它的次数。单独一个数的系数是它本身,而次数是0,单独一个字母的系数是1,次数也是1。
例2、指出下列单项式的系数与次数。
几个单项式的和叫做多项式(polynomial).多项式中每一个单项式叫做多项式的项,次数最高项的次数叫做多项式的次数。如x2+y2+1叫做二次三项式。
例1、下列代数式是多项式吗?若是,是几次几项式?
单项式与多项式统称为整式(integral expression)
三、阅读课本
P84-P87
四、补充练习
1、用代数式表示
(1)a与b的和的平方 (2)a与b的平方的和(平方和)
(3)与a+2d的和是4的数 (4)个位上的数是m,十位上的数是n的数
(5)x,y两数的差与x,y两数和的积 (6)比x的平方大3的数
2、用文字语言表示下列代数式的意义
(1)n表示整数,n(n+1)(n+2)表示_________________
(2)4a(a>0)可以表示_______________________
(3)2m+2n可以表示_______________________
3、说出下列代数式的实际意义
(1)ab
(2)abc
(3)2a+3b
4、12345是一个五位数,将数字1放到右边构成新的五位数23451,如果x是一个四位数,现在把数字1放在它的右边,得到一个五位数,用代数式如何表示这个新五位数?若将1放在左边,也可以得到一个五位数,又如何表示?
五、课堂小结
这节课你学会了什么?
六、课堂作业
作业纸
七、课后反馈
第4课时 求代数式的值
目的与要求 了解代数式的值的意义,能准确地求出代数式的值及按计算程序的步骤求值
知识与技能 通过代入法求值及设计程序求值培养学生良好的学习习惯和品质,提高运算能力与创新设计能力。
情感、态度与价值观 通过字母取不同的值的变化来认识世界发展变化及全面的观点。
教学过程
一、情境引入
某公园依地势摆若干个由大小相同的正方形构成的花坛,并在各正方形花坛的顶点与各边的中点布放盆花以营造节日气氛,
(1)填写下表
图形编号 (1) (2) (3) (4) …
盆花数
图形编号 (1) (2) (3) (4) (5) (6) …
火柴棒根数
(2)若要求第100个图案要用多少盆花,怎样去解答?
用火柴棒按图所示搭图
(1)填写下表
(2)你能说出第100个图形需多少根火柴棒吗?
解答:第1题8、13、18、23 8+5(n-1)
第2题:看正向三角形的个数,3×1=3、3×(1+2)=9、3×(1+2+3)=18、3×(1+2+3+4)=30、3×(1+2+3+4+5)=45、3×(1+2+3+4+5+6)=63、3×(1+2+3+…+n)=
二、新授
我们知道,用数值代替代数式里的字母,按照代数式指明的运算,计算出的结果,就叫做这个代数式的值。
1、单独字母代入法
(1)、当x=1时,求代数式4 -x+x2的值。
解:
(2)、已知a为3的倒数,b为最小的正整数,求代数式3a2-2ab+1的值
解答:
2、整体代入法
(3)、已知x2-2y+5=7,求3x2-6y-3的值。
解答:3
(4)、已知 ,求代数式 的值。
解:
三、课堂练习
练习本
四、课堂小结
这节课你学会了什么?
五、课堂作业
作业本
六、课后反馈
补充:
1、若|x|=2,|y|=1,求x2-2xy+y2的值
2、已知(x+2)2+|y+3|2+(z-4)2=0,求
第5课时 代数式的值
要求与目的 同上
知识与技能 同上
情感、态度与价值观 同上
教学过程
一、新授
1、观察下表
(1)在输出中写出符合所给表格规律的代数式
(2)设计求这个代数式值的计算程序图
(3)利用你所设计的计算程序求输入2005时的输出值。
解答:(1)3x+1,(2)
(3)6016
2、某移动公司开展两种业务“全球通”使用者缴50元月租费,然后通话1分钟再付话费0.4元;“神州行”不缴月租费,每通话1分钟,付话费0.6元。若一个月内通话x分钟
输入x -2 -1 0 1 2 3
输出 -5 -2 1 4 7 10
。
(1)用代数式表示两种方式的费用各多少?
(2)若某人估计一个月内通话300分钟,应选择哪一种方式更合算?
解答:50+0.4x,0.6x.选择第1种合适。
3、如图设计的程序,根据程序,单箭头上是所对应的运算,若输入的是5,求输出的结果,若输出的是5,求输入的值。
4、星期天,李师傅提着篮子(篮子的质量为0.5千克)去集市买10千克鸡蛋,当李师傅往篮子里拾称好的鸡蛋时,发现比过去买10千克鸡蛋的个数少了许多,于是将鸡蛋装进篮子再让摊主一起称,总质量为10.55千克,这时他要求摊主退1千克鸡蛋的钱,他是怎样知道摊主少称了大约1千克鸡蛋的呢?请将你的分析过程写出来。
解答:设实际质量为x
思考题
小李有2万元,想存入银行5年准备将来备用,跑到银行看到屏幕上显示的银行储蓄利息表(如下表)不知所措,你能帮帮他出主意吗?
在下列计算程序中填写适当的数或转换步骤
课堂小结
求代数式的值在实际问题中的应用
课堂作
定期 1年 2年 3年 5年
年利率(%) 2.25 2.43 2.7 2.88
业
作业本
课后反馈
第5课时 合并同类项
目的要求 理解同类项的概念、特征及合并方法
知识与技能 通过同类项的合并、培养学生分类归纳的能力
情感、态度与价值观 对事物的分类归纳,培养学生的严密的逻辑思维能力。
教学过程
一、情境引入
根据乘法的分配律可知:6×5+6×3=6×(5+3)=6×8=48
依照上述过程可得:5x+3x=
如图是学校校园的整体规划(单位:m)试计算这个学校的占地面积
用两种方法,方法1:(100+200)a+(100+200)b
方法2:100a+200a+240b+60b
二、新授
所含字母相同,并且相同字母的指数也相同的项是同类项(like terms)
例1、判断下列各组中的单项式是否为同类项,并说明理由
(1)3ac和-abc (2)-2x2y与4xy2 (3) (4)a2bc与-5a2bc3 (5)
(6)2×103t与1.5×102t
例2、若单项式2a2nbn-m与a6b是同类项,则nm的值是( )
A、5 B、6 C、8 D、9
根据乘法对加法的分配律把同类项合并成一项叫做合并同类项(unite like terms)
合并同类项的法则:
同类项的系数相加,所得的结果作为系数,字母与字母的指数不变。
例3、下列各式的计算是否正确?
(1)2x+3y=5xy (2)2a2+a2=2a4 (3)a2b-ba2=0 (3)4a2-6a2=-2
☆例4、合并同类项
(1)-3x+2y-5x-7y (2)a2-3ab+5-a2-3ab-7
(3)5m3-3m2n-m3+2nm2-7+2m3
★例4、求代数式的值
例5、已知多项式2x2+my-12与多项式nx2-3y+6的和中不含有x,y,试求mn的值。
竞赛之窗:设四位数 的各数字之和a+b+c+d是3的倍数,试说明 也是3的倍数。
解答: =1000a+100b+10c+d=(a+b+c+d)+(999a+99b+9c)=(a+b+c+d)+9(111a+11b+c)
显然(a+b+c+d)和9(111a+11b+c)都是3的倍数,所以, 是3的倍数。
三、课堂小结
这节课你学会了什么?
四、课堂练习
练习纸
五、课堂作业
作业本
六、课后反馈。
第6课时 去括号(一)
目的与要求 掌握去括号法则,进行整式的加减运算
知识与技能 通过去括号法则的发现过程来培养学生观察。分析、归纳能力
情感、态度与价值观 学会比较,通过比较见真知
教学过程
一、情境引入
1、用乘法的分配律计算:2×(2+3-4)=2×3+2×3+2×(-4)=6+6-8
-2×(2+3-4)=(-2)×2+(-2)×3+(-2)×(-4)=-4-6+8
你能发现,在上面的两个式子的去括号中,括号内每一项的符号是如何变化的?
如果将2和-2改为1或-1呢?
如果将2,+3,-4改成另一个单项式呢?
观察阅读课本P99页的情境,你发现了什么?请与同学们交流。
二、新授
去括号的法则
括号前面是“+”号,把括号和它前面的“+”号去掉,括号里各项的符号都不变号。
括号前面是“-”号,把括号和它前面的“-”号去掉,括号里各项的符号都要改变。
一般在去括号时,应先去小括号,再去中括号,最后去大括号。
例1、根据去括号法则,在__上填上“+”或“-”号
(1)a_______(-b+c)=a-b+c
(2)a_____(b-c+d)=a-b+c-d
(3)___(a-b)____(c-d)=a-b-c+d
☆例2、先去括号,再合并同类项
(1)5a-(2a-4b) (2)2x2+3(2x-x2)
★例2、先去括号,再合并同类项
(1)2a-3(a-4b)+3(2a-b) (2)2x-[x-(x2-x-3)-2]+2(2x2-3x+1) (3)-{-[a-(b-c)]}
例3、(1)已知一个多项式与a2-2a+2的和是a2+a-1,求这个多项式。
(2)已知A=x2-y2+z,B=2x2+y2+2z,求2A-B
练习
课本P102-103,1,2,3
例4已知m2+mn+2n2=11,mn+n2=6, 求m2+n2的值。
例5、已知有理数a,b,c在数轴上的位置如图,试化简|a+b|+|a-c|+2|a-b|
三、课堂小结
这一节课你学会了什么?
四、课堂练习
练习纸
五、课堂作业
作业纸
六、课后反馈
★★对于a随意取几个值,求代数式16+a-{8a-[a-9-(3-6a)]}的值,从中你能发现什么现象?试解释其中的原因。
若代数式(2x2+ax-y+6)-(2bx2-3x+5y-1)的值与字母x的取值无关,求代数式3(a2-2ab-b2)-(4a2+ab+b2)的值。
第7课时 去括号(二)
目的与要求 同上
知识与技能 同上
情感、态度与价值观 同上
教学教程
一、情境引入
准备三张如图所示的卡片
用它们拼成各种形状不同的四边形,
并计算它们的周长。
进行整式加减运算时,如果有括号先去括号,再合并同类项。
二、新授
例1、已知(x+3)2+|x+y+5|=0,求3x2y+{-2x2y-[-2xy+(x2y-4x20]-xy}的值。
解答:xy+4x2 42
例2、如图,所示的门框,上部是半圆形,下部是长方形,用4根长为a+b的可弯折的木条能制作出这样的门框吗?剩余或缺少多长(不计接缝)?
解答:
例3、a表示一个两位数,b表示一个三位数,把a放在b的左边,组成一个五位数x,把b放在a的左边也组成一个五位数y,试问9能整除x-y吗?
解答:x-y=(1000a+b)-(100b+a)=999a-99b=9(111a-11b)
即能被9整除。
例4某同学在做整式加减运算时,粗心大意,当将某整式减去xy-2yz+3xz时,误认为加上此式,所得答案为2yz-3xz+2xy,那么你能帮助他修改一下吗?
三、思考题
(1)以a随意取几个数,求代数式16+a-{8a-[a-9-(3-6a)]}的值,从中你能发现什么现象?试解释其中的原因。
(2)若代数式(2x2+ax-y+6)-(2bx2-3x+5y-1)的值与字母x的取值无关,求代数式3(a2-2ab-b2)-(4a2+ab+b2)的值。
四、课堂小结
这节课你学会了什么?
五、课堂练习
练习纸
六、课堂作业
作业本
七、课后反馈
本章小结
一、知识回顾
1、代数式
(1)代数式的概念:用数、字母和运算符号表示的式子叫做代数式。单独一个数或一个字母也叫做代数式。
(2)列代数式:
①代数式的基本写法
②如何用实际意义表示代数式
③如何将文字语言用代数式表示
(3)求代数式的值
①定义:将代数式中的字母用数来代替,并按照代数式所指明的运算求出的值。
②求代数式值的方法:
单独代入法:将代数式中的字母逐一代入再求值。
整体代入法:将含字母的项看成一个整体,将这个整体用数来代替再求值。
(3)整式
①单项式:数与字母的积的式子叫做单项式,数字因数叫做单项式的系数,所有字母的指数的和叫做单项式的次数。
②多项式:几个单项式的和叫做多项式,每一个单项式叫做这个多项式的项(注意它的符号),多项式中次数最高项的次数叫做多项式的次数。
③单项式与多项式统称为整式。
(4)同类项
①识别同类项:所含字母相同,相同字母的指数也相同的项,(如果两个多项式是相同的也可以看成同类项)
②合并同类项:先将它们的系数相加,作为结果的系数,字母与字母的指数不变。
(5)去括号:
①括号前面是“+”号,去掉“+”号与括号,里面各项不变号
②括号前面是“-”号,去掉“-”号与括号,里面各项都变号。
(5)数学思想
①整体与分类 ②特殊与一般
二、举例
分析课本P106页复习题
三、课堂小结
这节课本你学会了什么
四、课堂作业
作业纸
五、课堂反馈
1、若abx与ayb2是同类项,则下列结论正确的是( )
A.x=2,y=1 B.x=0,y=0 C.x=2,y=0 D.x=1,y=1
2、x-(2x-y)的运算结果是( )
A.-x+y B.-x-y C.x-y D.3x-y
3、如果代数式4y2-2y+5的值是7,则代数式2y2-y+1的值等于( )
A.2 B.3 C.-2 D.4
4、若x=1时,代数式ax3+bx+7的值是4,则当x=-1时,代数式ax3+bx+7的值是( )
A.7 B.12 C.11 D.10
5、某商场为了提高彩电销售人员的积极性,制定了新的工资分配方案,方案规定:每位销售人员的工资总额=基本工资+奖励工资。每位销售人员的月销售额为10000元,在销售定额内,得基本工资200元;超过销售定额,超过部分的销售额按相应比例作为奖励工资,奖励工资发放比例如下表
销售额 奖励工资比例
超过10000元不超过15000元的部分 5%
超过15000元不超过20000元的部分 8%
20000元以上的部分 10%
全月应纳税所得额 税率
不超过500元 5%
超过500元至2000元部分 10%
..... ........
:
依法纳税是每个公民应尽的义务,根据我国税法规定,全月工资总额不超过800元不要缴纳个人所得税,超过800元的部分为“全月应纳税所得额”,缴纳个人所得税税率表如下:
已知某销售人员每一月的销售额为a元(10000<a<15000),第二个月的销售额为b元(20000b
a
b
c
n
m
……
(1)
(2)
(3)
(4)
·
·
·
·
·
·
·
·
·
·
·
·
·
·
·
·
(1)
(2)
(3)
输入x
×3
+1
输出3x+1
输入a
a的倒数
a
输出结果
绝对值
-
×
输入2
( )
+1
输出___
输出25
( )
+1
输入__
输出-15
输入2
2
2
a
b
100
200
240
60
c
a
b
0
b
b
b
b
b
a
a
a
b
a
第1课时 字母表示数
目的与要求 领会用字母表示数是数量关系的一种抽象化,是代数的一个重要特点。
知识与技能 用字母表示数,了解抽象概括的思维方法。
情感、态度与价值观 初步认识辩证唯物主义观点--从特殊到一般。
教学过程
一、情境的引入
1、从日历中,观察后填写下表:
2、用火柴棒拼小鱼:
拼1、2、3条小鱼各用多少根火柴棒?拼20个小鱼呢?拼n条小鱼呢?
二、阅读课本
完成课本P79-82的内容
三、补充
1、(1)试比较a与-a的大小。
(2)已知n是整数。则①2n+3与②4n-1中,能表示“任意奇数”的是(
a
)
A、只有① B、只有②, C、两个都是 D、一个也没有
2、观察下列各式:9-1=8,16-4=12,25-9=16,36-16=20,…
这些等式反映自然数间的某种规律,设n(n≥1)表示自然数,用关于n的等式表示这个规律为_________
3、用字母表示下列图形中阴影部分的面积
4、某水库共有6个相同的泄洪闸,在无上游洪水的情况下,打开一个水闸泄洪使水库水位以a米/时匀速下降,汛期上游的洪水在未开泄洪闸的情况下使水库水位以b米/时匀速上升,当水库水位超警戒线h米时开始泄洪,如果打开n个水闸泄洪x小时,那么此时相对于警戒线的水面高度应为________。
解答:h+bx-nax
四、课堂练习
练习纸
五、课堂小结
这节课我们学会了什么?
六、课堂作业
见作业本
七、课后反馈
第2、3课时 代数式(第1课时代数式及有关概念,第2课时列代数式)
目的与要求 了解代数式的意义,知道一个代数式所表示的数量关系,会说出单项式的系数。
知识与技能 通过同一个代数式常常可以表示不同实际问题的数量关系,培养语言表达能力与发散思维能力。
情感、态度与价值观 培养学生实事求是、严谨的科学态度。
教学过程
一、情境引入
(1)求边长为a的正方形的周长和面积。
(2)求长a,宽为b的长方形的周长、面积。
(3)当路程为s,时间为t时,其速度为多少?
(4)长为a,宽为b,高为c的长方体的体积是多少?
二、新授
像上面的 的式子,都是由数、字母和运算符号构成的,称它们为代数式。(algebraic expression).单独的一个数和一个字母也是代数式。
例1、有下列各式
其中哪些是代数式?
像 ,abc都是数与字母的积,这样的代数式叫做单项式(monomial),单独一个数或一个字母也叫做单项式。单项式前面的数字因数叫做它的系数(coefficient)
单项式中所有字母的指数的和叫做它的次数。单独一个数的系数是它本身,而次数是0,单独一个字母的系数是1,次数也是1。
例2、指出下列单项式的系数与次数。
几个单项式的和叫做多项式(polynomial).多项式中每一个单项式叫做多项式的项,次数最高项的次数叫做多项式的次数。如x2+y2+1叫做二次三项式。
例1、下列代数式是多项式吗?若是,是几次几项式?
单项式与多项式统称为整式(integral expression)
三、阅读课本
P84-P87
四、补充练习
1、用代数式表示
(1)a与b的和的平方 (2)a与b的平方的和(平方和)
(3)与a+2d的和是4的数 (4)个位上的数是m,十位上的数是n的数
(5)x,y两数的差与x,y两数和的积 (6)比x的平方大3的数
2、用文字语言表示下列代数式的意义
(1)n表示整数,n(n+1)(n+2)表示_________________
(2)4a(a>0)可以表示_______________________
(3)2m+2n可以表示_______________________
3、说出下列代数式的实际意义
(1)ab
(2)abc
(3)2a+3b
4、12345是一个五位数,将数字1放到右边构成新的五位数23451,如果x是一个四位数,现在把数字1放在它的右边,得到一个五位数,用代数式如何表示这个新五位数?若将1放在左边,也可以得到一个五位数,又如何表示?
五、课堂小结
这节课你学会了什么?
六、课堂作业
作业纸
七、课后反馈
第4课时 求代数式的值
目的与要求 了解代数式的值的意义,能准确地求出代数式的值及按计算程序的步骤求值
知识与技能 通过代入法求值及设计程序求值培养学生良好的学习习惯和品质,提高运算能力与创新设计能力。
情感、态度与价值观 通过字母取不同的值的变化来认识世界发展变化及全面的观点。
教学过程
一、情境引入
某公园依地势摆若干个由大小相同的正方形构成的花坛,并在各正方形花坛的顶点与各边的中点布放盆花以营造节日气氛,
(1)填写下表
图形编号 (1) (2) (3) (4) …
盆花数
图形编号 (1) (2) (3) (4) (5) (6) …
火柴棒根数
(2)若要求第100个图案要用多少盆花,怎样去解答?
用火柴棒按图所示搭图
(1)填写下表
(2)你能说出第100个图形需多少根火柴棒吗?
解答:第1题8、13、18、23 8+5(n-1)
第2题:看正向三角形的个数,3×1=3、3×(1+2)=9、3×(1+2+3)=18、3×(1+2+3+4)=30、3×(1+2+3+4+5)=45、3×(1+2+3+4+5+6)=63、3×(1+2+3+…+n)=
二、新授
我们知道,用数值代替代数式里的字母,按照代数式指明的运算,计算出的结果,就叫做这个代数式的值。
1、单独字母代入法
(1)、当x=1时,求代数式4 -x+x2的值。
解:
(2)、已知a为3的倒数,b为最小的正整数,求代数式3a2-2ab+1的值
解答:
2、整体代入法
(3)、已知x2-2y+5=7,求3x2-6y-3的值。
解答:3
(4)、已知 ,求代数式 的值。
解:
三、课堂练习
练习本
四、课堂小结
这节课你学会了什么?
五、课堂作业
作业本
六、课后反馈
补充:
1、若|x|=2,|y|=1,求x2-2xy+y2的值
2、已知(x+2)2+|y+3|2+(z-4)2=0,求
第5课时 代数式的值
要求与目的 同上
知识与技能 同上
情感、态度与价值观 同上
教学过程
一、新授
1、观察下表
(1)在输出中写出符合所给表格规律的代数式
(2)设计求这个代数式值的计算程序图
(3)利用你所设计的计算程序求输入2005时的输出值。
解答:(1)3x+1,(2)
(3)6016
2、某移动公司开展两种业务“全球通”使用者缴50元月租费,然后通话1分钟再付话费0.4元;“神州行”不缴月租费,每通话1分钟,付话费0.6元。若一个月内通话x分钟
输入x -2 -1 0 1 2 3
输出 -5 -2 1 4 7 10
。
(1)用代数式表示两种方式的费用各多少?
(2)若某人估计一个月内通话300分钟,应选择哪一种方式更合算?
解答:50+0.4x,0.6x.选择第1种合适。
3、如图设计的程序,根据程序,单箭头上是所对应的运算,若输入的是5,求输出的结果,若输出的是5,求输入的值。
4、星期天,李师傅提着篮子(篮子的质量为0.5千克)去集市买10千克鸡蛋,当李师傅往篮子里拾称好的鸡蛋时,发现比过去买10千克鸡蛋的个数少了许多,于是将鸡蛋装进篮子再让摊主一起称,总质量为10.55千克,这时他要求摊主退1千克鸡蛋的钱,他是怎样知道摊主少称了大约1千克鸡蛋的呢?请将你的分析过程写出来。
解答:设实际质量为x
思考题
小李有2万元,想存入银行5年准备将来备用,跑到银行看到屏幕上显示的银行储蓄利息表(如下表)不知所措,你能帮帮他出主意吗?
在下列计算程序中填写适当的数或转换步骤
课堂小结
求代数式的值在实际问题中的应用
课堂作
定期 1年 2年 3年 5年
年利率(%) 2.25 2.43 2.7 2.88
业
作业本
课后反馈
第5课时 合并同类项
目的要求 理解同类项的概念、特征及合并方法
知识与技能 通过同类项的合并、培养学生分类归纳的能力
情感、态度与价值观 对事物的分类归纳,培养学生的严密的逻辑思维能力。
教学过程
一、情境引入
根据乘法的分配律可知:6×5+6×3=6×(5+3)=6×8=48
依照上述过程可得:5x+3x=
如图是学校校园的整体规划(单位:m)试计算这个学校的占地面积
用两种方法,方法1:(100+200)a+(100+200)b
方法2:100a+200a+240b+60b
二、新授
所含字母相同,并且相同字母的指数也相同的项是同类项(like terms)
例1、判断下列各组中的单项式是否为同类项,并说明理由
(1)3ac和-abc (2)-2x2y与4xy2 (3) (4)a2bc与-5a2bc3 (5)
(6)2×103t与1.5×102t
例2、若单项式2a2nbn-m与a6b是同类项,则nm的值是( )
A、5 B、6 C、8 D、9
根据乘法对加法的分配律把同类项合并成一项叫做合并同类项(unite like terms)
合并同类项的法则:
同类项的系数相加,所得的结果作为系数,字母与字母的指数不变。
例3、下列各式的计算是否正确?
(1)2x+3y=5xy (2)2a2+a2=2a4 (3)a2b-ba2=0 (3)4a2-6a2=-2
☆例4、合并同类项
(1)-3x+2y-5x-7y (2)a2-3ab+5-a2-3ab-7
(3)5m3-3m2n-m3+2nm2-7+2m3
★例4、求代数式的值
例5、已知多项式2x2+my-12与多项式nx2-3y+6的和中不含有x,y,试求mn的值。
竞赛之窗:设四位数 的各数字之和a+b+c+d是3的倍数,试说明 也是3的倍数。
解答: =1000a+100b+10c+d=(a+b+c+d)+(999a+99b+9c)=(a+b+c+d)+9(111a+11b+c)
显然(a+b+c+d)和9(111a+11b+c)都是3的倍数,所以, 是3的倍数。
三、课堂小结
这节课你学会了什么?
四、课堂练习
练习纸
五、课堂作业
作业本
六、课后反馈。
第6课时 去括号(一)
目的与要求 掌握去括号法则,进行整式的加减运算
知识与技能 通过去括号法则的发现过程来培养学生观察。分析、归纳能力
情感、态度与价值观 学会比较,通过比较见真知
教学过程
一、情境引入
1、用乘法的分配律计算:2×(2+3-4)=2×3+2×3+2×(-4)=6+6-8
-2×(2+3-4)=(-2)×2+(-2)×3+(-2)×(-4)=-4-6+8
你能发现,在上面的两个式子的去括号中,括号内每一项的符号是如何变化的?
如果将2和-2改为1或-1呢?
如果将2,+3,-4改成另一个单项式呢?
观察阅读课本P99页的情境,你发现了什么?请与同学们交流。
二、新授
去括号的法则
括号前面是“+”号,把括号和它前面的“+”号去掉,括号里各项的符号都不变号。
括号前面是“-”号,把括号和它前面的“-”号去掉,括号里各项的符号都要改变。
一般在去括号时,应先去小括号,再去中括号,最后去大括号。
例1、根据去括号法则,在__上填上“+”或“-”号
(1)a_______(-b+c)=a-b+c
(2)a_____(b-c+d)=a-b+c-d
(3)___(a-b)____(c-d)=a-b-c+d
☆例2、先去括号,再合并同类项
(1)5a-(2a-4b) (2)2x2+3(2x-x2)
★例2、先去括号,再合并同类项
(1)2a-3(a-4b)+3(2a-b) (2)2x-[x-(x2-x-3)-2]+2(2x2-3x+1) (3)-{-[a-(b-c)]}
例3、(1)已知一个多项式与a2-2a+2的和是a2+a-1,求这个多项式。
(2)已知A=x2-y2+z,B=2x2+y2+2z,求2A-B
练习
课本P102-103,1,2,3
例4已知m2+mn+2n2=11,mn+n2=6, 求m2+n2的值。
例5、已知有理数a,b,c在数轴上的位置如图,试化简|a+b|+|a-c|+2|a-b|
三、课堂小结
这一节课你学会了什么?
四、课堂练习
练习纸
五、课堂作业
作业纸
六、课后反馈
★★对于a随意取几个值,求代数式16+a-{8a-[a-9-(3-6a)]}的值,从中你能发现什么现象?试解释其中的原因。
若代数式(2x2+ax-y+6)-(2bx2-3x+5y-1)的值与字母x的取值无关,求代数式3(a2-2ab-b2)-(4a2+ab+b2)的值。
第7课时 去括号(二)
目的与要求 同上
知识与技能 同上
情感、态度与价值观 同上
教学教程
一、情境引入
准备三张如图所示的卡片
用它们拼成各种形状不同的四边形,
并计算它们的周长。
进行整式加减运算时,如果有括号先去括号,再合并同类项。
二、新授
例1、已知(x+3)2+|x+y+5|=0,求3x2y+{-2x2y-[-2xy+(x2y-4x20]-xy}的值。
解答:xy+4x2 42
例2、如图,所示的门框,上部是半圆形,下部是长方形,用4根长为a+b的可弯折的木条能制作出这样的门框吗?剩余或缺少多长(不计接缝)?
解答:
例3、a表示一个两位数,b表示一个三位数,把a放在b的左边,组成一个五位数x,把b放在a的左边也组成一个五位数y,试问9能整除x-y吗?
解答:x-y=(1000a+b)-(100b+a)=999a-99b=9(111a-11b)
即能被9整除。
例4某同学在做整式加减运算时,粗心大意,当将某整式减去xy-2yz+3xz时,误认为加上此式,所得答案为2yz-3xz+2xy,那么你能帮助他修改一下吗?
三、思考题
(1)以a随意取几个数,求代数式16+a-{8a-[a-9-(3-6a)]}的值,从中你能发现什么现象?试解释其中的原因。
(2)若代数式(2x2+ax-y+6)-(2bx2-3x+5y-1)的值与字母x的取值无关,求代数式3(a2-2ab-b2)-(4a2+ab+b2)的值。
四、课堂小结
这节课你学会了什么?
五、课堂练习
练习纸
六、课堂作业
作业本
七、课后反馈
本章小结
一、知识回顾
1、代数式
(1)代数式的概念:用数、字母和运算符号表示的式子叫做代数式。单独一个数或一个字母也叫做代数式。
(2)列代数式:
①代数式的基本写法
②如何用实际意义表示代数式
③如何将文字语言用代数式表示
(3)求代数式的值
①定义:将代数式中的字母用数来代替,并按照代数式所指明的运算求出的值。
②求代数式值的方法:
单独代入法:将代数式中的字母逐一代入再求值。
整体代入法:将含字母的项看成一个整体,将这个整体用数来代替再求值。
(3)整式
①单项式:数与字母的积的式子叫做单项式,数字因数叫做单项式的系数,所有字母的指数的和叫做单项式的次数。
②多项式:几个单项式的和叫做多项式,每一个单项式叫做这个多项式的项(注意它的符号),多项式中次数最高项的次数叫做多项式的次数。
③单项式与多项式统称为整式。
(4)同类项
①识别同类项:所含字母相同,相同字母的指数也相同的项,(如果两个多项式是相同的也可以看成同类项)
②合并同类项:先将它们的系数相加,作为结果的系数,字母与字母的指数不变。
(5)去括号:
①括号前面是“+”号,去掉“+”号与括号,里面各项不变号
②括号前面是“-”号,去掉“-”号与括号,里面各项都变号。
(5)数学思想
①整体与分类 ②特殊与一般
二、举例
分析课本P106页复习题
三、课堂小结
这节课本你学会了什么
四、课堂作业
作业纸
五、课堂反馈
1、若abx与ayb2是同类项,则下列结论正确的是( )
A.x=2,y=1 B.x=0,y=0 C.x=2,y=0 D.x=1,y=1
2、x-(2x-y)的运算结果是( )
A.-x+y B.-x-y C.x-y D.3x-y
3、如果代数式4y2-2y+5的值是7,则代数式2y2-y+1的值等于( )
A.2 B.3 C.-2 D.4
4、若x=1时,代数式ax3+bx+7的值是4,则当x=-1时,代数式ax3+bx+7的值是( )
A.7 B.12 C.11 D.10
5、某商场为了提高彩电销售人员的积极性,制定了新的工资分配方案,方案规定:每位销售人员的工资总额=基本工资+奖励工资。每位销售人员的月销售额为10000元,在销售定额内,得基本工资200元;超过销售定额,超过部分的销售额按相应比例作为奖励工资,奖励工资发放比例如下表
销售额 奖励工资比例
超过10000元不超过15000元的部分 5%
超过15000元不超过20000元的部分 8%
20000元以上的部分 10%
全月应纳税所得额 税率
不超过500元 5%
超过500元至2000元部分 10%
..... ........
:
依法纳税是每个公民应尽的义务,根据我国税法规定,全月工资总额不超过800元不要缴纳个人所得税,超过800元的部分为“全月应纳税所得额”,缴纳个人所得税税率表如下:
已知某销售人员每一月的销售额为a元(10000<a<15000),第二个月的销售额为b元(20000
a
b
c
n
m
……
(1)
(2)
(3)
(4)
·
·
·
·
·
·
·
·
·
·
·
·
·
·
·
·
(1)
(2)
(3)
输入x
×3
+1
输出3x+1
输入a
a的倒数
a
输出结果
绝对值
-
×
输入2
( )
+1
输出___
输出25
( )
+1
输入__
输出-15
输入2
2
2
a
b
100
200
240
60
c
a
b
0
b
b
b
b
b
a
a
a
b
a
同课章节目录
- 第1章 我们与数学同行
- 1.1 生活 数学
- 1.2 活动 思考
- 第2章 有理数
- 2.1 正数与负数
- 2.2 有理数与无理数
- 2.3 数轴
- 2.4 绝对值与相反数
- 2.5 有理数的加法与减法
- 2.6 有理数的乘法与除法
- 2.7 有理数的乘方
- 2.8 有理数的混合运算
- 第3章 代数式
- 3.1 字母表示数
- 3.2 代数式
- 3.3 代数式的值
- 3.4 合并同类项
- 3.5 去括号
- 3.6 整式的加减
- 第4章 一元一次方程
- 4.1 从问题到方程
- 4.2 解一元一次方程
- 4.3 用一元一次方程解决问题
- 第5章 走进图形世界
- 5.1 丰富的图形世界
- 5.2 图形的运动
- 5.3 展开与折叠
- 5.4 主视图、左视图、俯视图
- 第6章 平面图形的认识(一)
- 6.1 线段 射线 直线
- 6.2 角
- 6.3 余角 补角 对顶角
- 6.4 平行
- 6.5 垂直
