江苏省南京市南师附中2020-2021学年高二下学期期中考试复习卷数学试题 Word版含答案
文档属性
| 名称 | 江苏省南京市南师附中2020-2021学年高二下学期期中考试复习卷数学试题 Word版含答案 |  | |
| 格式 | docx | ||
| 文件大小 | 793.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-04-18 20:26:20 | ||
图片预览




文档简介
2020-2021学年第二学期南师附中期中复习卷
高二数学
一、单选题(共8题,每题5分,共40分)
1.已知false,false,则“false”是“false”的
A.充分不必要条件 B.必要不充分条件
C.充分必要条件 D.既不充分也不必要条件
2.已知false,其中false为虚数单位,则复数false在复平面内对应的点在
A.第一象限 B.第二象限 C.第三象限 D.第四象限
3.函数false的部分图像大致为
A. B.
C. D.
4.甲乙两人进行扑克牌得分比赛,甲的三张扑克牌分别记为false,false,false,乙的三张扑克牌分别记为false,false,false.这六张扑克牌的大小顺序为false.比赛规则为:每张牌只能出一次,每局比赛双方各出一张牌,共比赛三局,在每局比赛中牌大者得1分,牌小者得0分.若每局比赛之前彼此都不知道对方所出之牌,则六张牌都出完时乙得2分的概率为
A.false B.false C.false D. false
5.在等差数列false中,若false,则有等式false(false且false)成立,类比上述性质,在等比数列false中,若false,则有
A.false(false且false)
B.false(false且false)
C.false(false且false)
D.false(false且false)
6.在长方体false中,false,false,点false为false的中点,若三棱锥false的所有顶点都在球false的球面上,则球false的表面积为
A.false B.false C.false D.false
7.如图,斜线段false与平面false所成的角为false,false为斜足.平面false上的动点false满足false,则点false的轨迹为
A.圆 B.椭圆
C.双曲线的一部分 D.抛物线的一部分
8.已知false是自然对数的底数,设false,则
A.false B.false C.false D.false
二、多选题(共4题,每题5分,共20分:漏选得2分,错选或不选得0分)
right2660659.由等边三角形组成的网格如图所示,多边形false是某几何体的表面展开图,对于该几何体(顶点的字母用展开图相应字母表示,对于重合的两点,取字母表中靠前的字母表示),下列结论中不正确的是
A.false平面false
B.平面false平面false
C.平面false平面false
D.false
10.已知双曲线false的左、右两个焦点分别为false,直线false与C交于false两点,false轴,垂足为E,直线false与C的另一个交点为P,则下列结论正确的是
A.四边形false为平行四边形 B.false
C.直线false的斜率为false D.false
11.已知函数false,则下列结论正确的有
A.函数false的最小正周期为false B.函数false在false上有2个零点
C.函数false的图象关于false对称 D.函数false的最小值为false
4212590115125512.“悬链线”进入公众视野,源于达芬奇的画作《抱银貂的女人》。这幅画作中,女士脖颈上悬挂的黑色珍珠链与主人相互映衬,显现出不一样的美与光泽.而达芬奇却心生好奇:“固定项链的两端,使其在重力作用下自然下垂,那么项链所形成的曲线是什么?”随着后人研究的深入,悬链线的庐山真面目被揭开。法国著名昆虫学家、文学家法布尔在《昆虫记》里有这样的记载:“每当地心引力和扰性同时发生作用时,悬链线就在现实中出现了。当一条悬链弯曲成两点不在同一垂直线(注:垂直于地面的直线)上的曲线时,人们便把这曲线称为悬链线。这就是一条软绳子两端抓住而垂下来的形状,这就是一张被风鼓起来的船帆外形的那条线条。”建立适当的平面直角坐标系,可以写出悬链线的函数解析式:false,其中false为悬链线系数。当a =1时,false称为双曲余弦函数,记为false。类似的双曲正弦函数false.直线false与false和false的图像分别交于点false、false.下列结论正确的是
A.false B.false
C.false随false的增大而减小 D.false与false的图像有完全相同的渐近线
三、填空题(共4题,每题5分,共20分)
13.两对夫妻准备周末出去旅游,有甲?乙?丙?丁四辆顺风车可以搭乘,其中甲?乙两车每辆最多可搭乘两人,丙?丁两车每辆最多可搭乘一人,不是夫妻的两个人不能搭乘同一辆车,若不考虑座位顺序,且这两对夫妻都要坐上车.则不同的搭乘方案共有___________种.
14.设复数z,满足false,false,false,则false____________.
15.已知离心率为2的双曲线false:false的右焦点false与抛物线false的焦点重合,false的中心与false的顶点重合,false是false与false的公共点,若false,则false的标准方程为______.
16.设false,false,false,false,则false的值域是 ,函数false在false的最大值是false,则false的值是______
四、解答题(共6题,共70分)
17.(10分)在①false,②false,③false这三个条件中任选一个,补充在下面问题中,若问题中的三角形存在,求false的值;若问题中的三角形不存在,请明理由.
问题:是否存在false,它的内角A,B,C的对边分别为a,b,c,且c=3,false,______?
18.(12分)已知等差数列false和等比数列false满足false,false,false,false.
(1)求数列false,false的通项公式;
(2)设数列false中不在数列false中的项按从小到大的顺序构成数列false,记数列false的前false项和为false,求false.
19.(12分)2020年10月份南京市某开发区一企业顺利开工复产,该企业生产不同规格的一种产品,根据检测标准,其合格产品的质量y(单位:false)与尺寸x(单位:false )之间近似满足关系式false(b?c为大于0的常数).按照某项指标测定,当产品质量与尺寸的比在区间false内时为优等品.现随机抽取6件合格产品,测得数据如下:
尺寸false
38
48
58
68
78
88
质量false
16.8
18.8
20.7
22.4
24
25.5
质量与尺寸的比false
0.442
0.392
0.357
0.329
0.308
0.290
(1)现从抽取的6件合格产品中再任选3件,记false为取到优等品的件数试求随机变量false的分布列和期望;
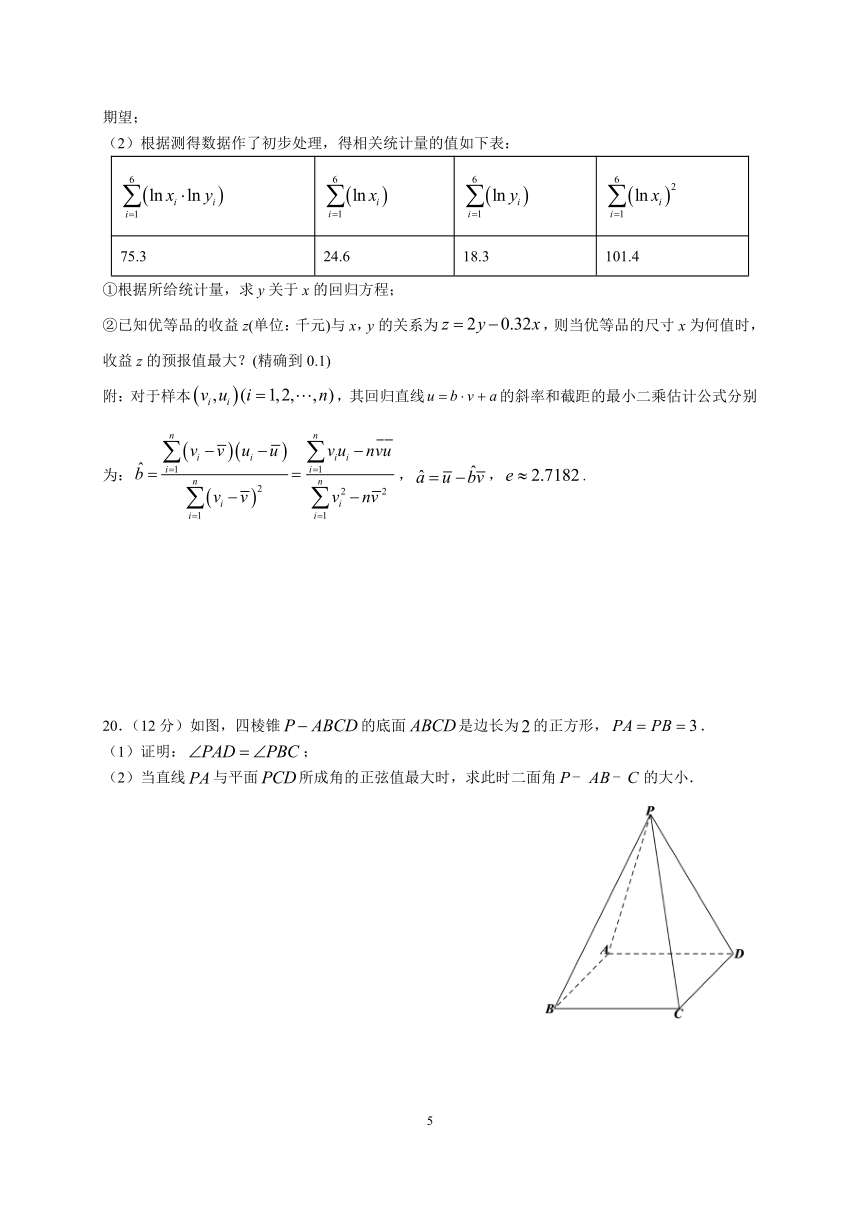
(2)根据测得数据作了初步处理,得相关统计量的值如下表:
false
false
false
false
75.3
24.6
18.3
101.4
①根据所给统计量,求y关于x的回归方程;
②已知优等品的收益z(单位:千元)与x,y的关系为false,则当优等品的尺寸x为何值时,收益z的预报值最大?(精确到0.1)
附:对于样本false,其回归直线false的斜率和截距的最小二乘估计公式分别为:false,false,false.
20.(12分)如图,四棱锥false的底面false是边长为false的正方形,false.
(1)证明:false;
(2)当直线false与平面false所成角的正弦值最大时,求此时二面角false的大小.
3892550139700
343471580708521.(12分)如图,已知椭圆false的右焦点为false,原点为false,椭圆的动弦false过焦点false且不垂直于坐标轴,弦false的中点为false,椭圆false在点false处的两切线的交点为false.
(1)求证:false三点共线;
(2)求false的最小值.
22.(12分)已知函数false,false是自然对数的底数.
(1)求曲线false在false处的切线方程;
(2)若false,证明:曲线false不落在false图像的下方.
参考答案
1
2
3
4
5
6
7
8
B
D
D
C
A
D
B
A
9
10
11
12
ACD
AC
BC
AC
13. 50
14.false
15.false
16.false false
17. 由false及余弦定理可得
false.
因为false,于是
false(*).
方案一:选条件①.
由false和正弦弦定理得false,代入(*)解得false,false.
因此,选条件①时,问题中的三角形存在,此时false.
方案二:选条件②.
由于false得false,代入(*)得
false.
因为false,所以false不存在.
因此,选条件②时,问题中的三角形不存在.
方案三:选条件③.
因为false,false,由余弦定理可得
false.
代入(*)得false,因此,选条件③时,问题中的三角形不存在.
18. (1)设等差数列false的公差为false,
因为false,所以false,
所以false.
所以false.
又false,即false,所以false
所以false.
(2)由(1)false,
即false是数列false中的第false项.
设数列false的前false项和为false,数列false的前false项和为false,
因为false,false,
所以数列false的前100项是由数列false的前107项去掉数列false的前7项后构成的,
所以false
falsefalse.
19. (1)由已知,优等品的质量与尺寸的比在区间false内,即false
则随机抽取的6件合格产品中,有3件为优等品,3件为非优等品.
现从抽取的6件合格产品中再任选3件,则取到优等品的件数false
false,false,
false,false
false的分布列为
false
0
1
2
3
false
false
false
false
false
∴false
(2)对false两边取自然对数得false,
令false,得false,且false,
①根据所给统计量及最小二乘估计公式有:
false
false,得false,故false
所求y关于x的回归方程为false
② 由① 可知,false,则false
由优等品质量与尺寸的比false,即false.
令false,false
当false时,false取最大值,
即优等品的尺寸false,收益false的预报值最大.
20. (1)分别取false、false的中点false、false,连接false、false、false.
因为false,false为false的中点,所以false.
又因为false,所以false.
因为四边形false为正方形,则false且false,
false、false分别为false、false的中点,false且false,
false,所以,四边形false为矩形,则false,
false,所以false平面false.
因为false平面false,所以false.
在false中,false为false的中点,false,所以false.
又因为false,false,所以false,从而可得false;
(2)由(1)可知,false平面false,false,false平面false,
false平面false,false,所以,false为二面角false的平面角,且false,
以点false为坐标原点,false、false所在直线分别为false、false轴建立如下图所示的空间直角坐标系,
设false,其中false,则false、false、false、false、false、false,
false,false,false,
设平面false的法向量为false,
由false,即false,
取false,则false,false,false,
falsefalse,
令false,则false,
则false,
当且仅当false时,即当false时,即当false时,等号成立.
所以,当直线false与平面false所成角的正弦值最大时,二面角false为false.
21. (1)椭圆的右焦点为false,
设false所在的直线的方程为false,且false
联立方程组false可得:false
则false,false,点false的坐标为false,
false所在的直线的方程为false,
设在点false处的切线为:false,与椭圆联立后由false,可得false,整理得:椭圆false在false处的切线方程为false,false,
联立方程组false,
解得点false的坐标为false,
false,
故false三点共线.
(2)由(1)可知,false
false
false
false
false,
当且仅当false即false时,等号成立.
22. (1)解:由题意知,false,故false,而false,
故所求切线方程为false,即false.
(2)证明:要证曲线false不落在false图像的下方,
即证false,即证false.
令false,false,false.false,
令false,得false;令false,得false或false,
所以当false时,false取得极大值,且极大值为2.而false,
易知false在false上单调递增,且false.
令false,得false,令false,得false,故false.
故当false时,false.设false,
则false.设false,则false.
设false,则false,易知false在false上单调递增,
则false,则false在false上单调递增,
从而false,则false在false上单调递增,
则false,从而false在false上单调递增,
所以当false时,false,故当false时,false.
综上所述,当false时,曲线false不落在false图像的下方.
高二数学
一、单选题(共8题,每题5分,共40分)
1.已知false,false,则“false”是“false”的
A.充分不必要条件 B.必要不充分条件
C.充分必要条件 D.既不充分也不必要条件
2.已知false,其中false为虚数单位,则复数false在复平面内对应的点在
A.第一象限 B.第二象限 C.第三象限 D.第四象限
3.函数false的部分图像大致为
A. B.
C. D.
4.甲乙两人进行扑克牌得分比赛,甲的三张扑克牌分别记为false,false,false,乙的三张扑克牌分别记为false,false,false.这六张扑克牌的大小顺序为false.比赛规则为:每张牌只能出一次,每局比赛双方各出一张牌,共比赛三局,在每局比赛中牌大者得1分,牌小者得0分.若每局比赛之前彼此都不知道对方所出之牌,则六张牌都出完时乙得2分的概率为
A.false B.false C.false D. false
5.在等差数列false中,若false,则有等式false(false且false)成立,类比上述性质,在等比数列false中,若false,则有
A.false(false且false)
B.false(false且false)
C.false(false且false)
D.false(false且false)
6.在长方体false中,false,false,点false为false的中点,若三棱锥false的所有顶点都在球false的球面上,则球false的表面积为
A.false B.false C.false D.false
7.如图,斜线段false与平面false所成的角为false,false为斜足.平面false上的动点false满足false,则点false的轨迹为
A.圆 B.椭圆
C.双曲线的一部分 D.抛物线的一部分
8.已知false是自然对数的底数,设false,则
A.false B.false C.false D.false
二、多选题(共4题,每题5分,共20分:漏选得2分,错选或不选得0分)
right2660659.由等边三角形组成的网格如图所示,多边形false是某几何体的表面展开图,对于该几何体(顶点的字母用展开图相应字母表示,对于重合的两点,取字母表中靠前的字母表示),下列结论中不正确的是
A.false平面false
B.平面false平面false
C.平面false平面false
D.false
10.已知双曲线false的左、右两个焦点分别为false,直线false与C交于false两点,false轴,垂足为E,直线false与C的另一个交点为P,则下列结论正确的是
A.四边形false为平行四边形 B.false
C.直线false的斜率为false D.false
11.已知函数false,则下列结论正确的有
A.函数false的最小正周期为false B.函数false在false上有2个零点
C.函数false的图象关于false对称 D.函数false的最小值为false
4212590115125512.“悬链线”进入公众视野,源于达芬奇的画作《抱银貂的女人》。这幅画作中,女士脖颈上悬挂的黑色珍珠链与主人相互映衬,显现出不一样的美与光泽.而达芬奇却心生好奇:“固定项链的两端,使其在重力作用下自然下垂,那么项链所形成的曲线是什么?”随着后人研究的深入,悬链线的庐山真面目被揭开。法国著名昆虫学家、文学家法布尔在《昆虫记》里有这样的记载:“每当地心引力和扰性同时发生作用时,悬链线就在现实中出现了。当一条悬链弯曲成两点不在同一垂直线(注:垂直于地面的直线)上的曲线时,人们便把这曲线称为悬链线。这就是一条软绳子两端抓住而垂下来的形状,这就是一张被风鼓起来的船帆外形的那条线条。”建立适当的平面直角坐标系,可以写出悬链线的函数解析式:false,其中false为悬链线系数。当a =1时,false称为双曲余弦函数,记为false。类似的双曲正弦函数false.直线false与false和false的图像分别交于点false、false.下列结论正确的是
A.false B.false
C.false随false的增大而减小 D.false与false的图像有完全相同的渐近线
三、填空题(共4题,每题5分,共20分)
13.两对夫妻准备周末出去旅游,有甲?乙?丙?丁四辆顺风车可以搭乘,其中甲?乙两车每辆最多可搭乘两人,丙?丁两车每辆最多可搭乘一人,不是夫妻的两个人不能搭乘同一辆车,若不考虑座位顺序,且这两对夫妻都要坐上车.则不同的搭乘方案共有___________种.
14.设复数z,满足false,false,false,则false____________.
15.已知离心率为2的双曲线false:false的右焦点false与抛物线false的焦点重合,false的中心与false的顶点重合,false是false与false的公共点,若false,则false的标准方程为______.
16.设false,false,false,false,则false的值域是 ,函数false在false的最大值是false,则false的值是______
四、解答题(共6题,共70分)
17.(10分)在①false,②false,③false这三个条件中任选一个,补充在下面问题中,若问题中的三角形存在,求false的值;若问题中的三角形不存在,请明理由.
问题:是否存在false,它的内角A,B,C的对边分别为a,b,c,且c=3,false,______?
18.(12分)已知等差数列false和等比数列false满足false,false,false,false.
(1)求数列false,false的通项公式;
(2)设数列false中不在数列false中的项按从小到大的顺序构成数列false,记数列false的前false项和为false,求false.
19.(12分)2020年10月份南京市某开发区一企业顺利开工复产,该企业生产不同规格的一种产品,根据检测标准,其合格产品的质量y(单位:false)与尺寸x(单位:false )之间近似满足关系式false(b?c为大于0的常数).按照某项指标测定,当产品质量与尺寸的比在区间false内时为优等品.现随机抽取6件合格产品,测得数据如下:
尺寸false
38
48
58
68
78
88
质量false
16.8
18.8
20.7
22.4
24
25.5
质量与尺寸的比false
0.442
0.392
0.357
0.329
0.308
0.290
(1)现从抽取的6件合格产品中再任选3件,记false为取到优等品的件数试求随机变量false的分布列和期望;
(2)根据测得数据作了初步处理,得相关统计量的值如下表:
false
false
false
false
75.3
24.6
18.3
101.4
①根据所给统计量,求y关于x的回归方程;
②已知优等品的收益z(单位:千元)与x,y的关系为false,则当优等品的尺寸x为何值时,收益z的预报值最大?(精确到0.1)
附:对于样本false,其回归直线false的斜率和截距的最小二乘估计公式分别为:false,false,false.
20.(12分)如图,四棱锥false的底面false是边长为false的正方形,false.
(1)证明:false;
(2)当直线false与平面false所成角的正弦值最大时,求此时二面角false的大小.
3892550139700
343471580708521.(12分)如图,已知椭圆false的右焦点为false,原点为false,椭圆的动弦false过焦点false且不垂直于坐标轴,弦false的中点为false,椭圆false在点false处的两切线的交点为false.
(1)求证:false三点共线;
(2)求false的最小值.
22.(12分)已知函数false,false是自然对数的底数.
(1)求曲线false在false处的切线方程;
(2)若false,证明:曲线false不落在false图像的下方.
参考答案
1
2
3
4
5
6
7
8
B
D
D
C
A
D
B
A
9
10
11
12
ACD
AC
BC
AC
13. 50
14.false
15.false
16.false false
17. 由false及余弦定理可得
false.
因为false,于是
false(*).
方案一:选条件①.
由false和正弦弦定理得false,代入(*)解得false,false.
因此,选条件①时,问题中的三角形存在,此时false.
方案二:选条件②.
由于false得false,代入(*)得
false.
因为false,所以false不存在.
因此,选条件②时,问题中的三角形不存在.
方案三:选条件③.
因为false,false,由余弦定理可得
false.
代入(*)得false,因此,选条件③时,问题中的三角形不存在.
18. (1)设等差数列false的公差为false,
因为false,所以false,
所以false.
所以false.
又false,即false,所以false
所以false.
(2)由(1)false,
即false是数列false中的第false项.
设数列false的前false项和为false,数列false的前false项和为false,
因为false,false,
所以数列false的前100项是由数列false的前107项去掉数列false的前7项后构成的,
所以false
falsefalse.
19. (1)由已知,优等品的质量与尺寸的比在区间false内,即false
则随机抽取的6件合格产品中,有3件为优等品,3件为非优等品.
现从抽取的6件合格产品中再任选3件,则取到优等品的件数false
false,false,
false,false
false的分布列为
false
0
1
2
3
false
false
false
false
false
∴false
(2)对false两边取自然对数得false,
令false,得false,且false,
①根据所给统计量及最小二乘估计公式有:
false
false,得false,故false
所求y关于x的回归方程为false
② 由① 可知,false,则false
由优等品质量与尺寸的比false,即false.
令false,false
当false时,false取最大值,
即优等品的尺寸false,收益false的预报值最大.
20. (1)分别取false、false的中点false、false,连接false、false、false.
因为false,false为false的中点,所以false.
又因为false,所以false.
因为四边形false为正方形,则false且false,
false、false分别为false、false的中点,false且false,
false,所以,四边形false为矩形,则false,
false,所以false平面false.
因为false平面false,所以false.
在false中,false为false的中点,false,所以false.
又因为false,false,所以false,从而可得false;
(2)由(1)可知,false平面false,false,false平面false,
false平面false,false,所以,false为二面角false的平面角,且false,
以点false为坐标原点,false、false所在直线分别为false、false轴建立如下图所示的空间直角坐标系,
设false,其中false,则false、false、false、false、false、false,
false,false,false,
设平面false的法向量为false,
由false,即false,
取false,则false,false,false,
falsefalse,
令false,则false,
则false,
当且仅当false时,即当false时,即当false时,等号成立.
所以,当直线false与平面false所成角的正弦值最大时,二面角false为false.
21. (1)椭圆的右焦点为false,
设false所在的直线的方程为false,且false
联立方程组false可得:false
则false,false,点false的坐标为false,
false所在的直线的方程为false,
设在点false处的切线为:false,与椭圆联立后由false,可得false,整理得:椭圆false在false处的切线方程为false,false,
联立方程组false,
解得点false的坐标为false,
false,
故false三点共线.
(2)由(1)可知,false
false
false
false
false,
当且仅当false即false时,等号成立.
22. (1)解:由题意知,false,故false,而false,
故所求切线方程为false,即false.
(2)证明:要证曲线false不落在false图像的下方,
即证false,即证false.
令false,false,false.false,
令false,得false;令false,得false或false,
所以当false时,false取得极大值,且极大值为2.而false,
易知false在false上单调递增,且false.
令false,得false,令false,得false,故false.
故当false时,false.设false,
则false.设false,则false.
设false,则false,易知false在false上单调递增,
则false,则false在false上单调递增,
从而false,则false在false上单调递增,
则false,从而false在false上单调递增,
所以当false时,false,故当false时,false.
综上所述,当false时,曲线false不落在false图像的下方.
同课章节目录
