19.3 方案选择 课件(共22张PPT)
文档属性
| 名称 | 19.3 方案选择 课件(共22张PPT) |
|
|
| 格式 | pptx | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-04-18 00:00:00 | ||
图片预览




文档简介
19.3 选择方案
第十九章 一次函数
2021年春人教版八年级(下)数学
1、会用一次函数知识解决方案选择问题,体会函数模型思想。
2、能从不同的角度思考问题,优化解决问题的方法。
如何用一次函数选择最佳方案。(重点)
能从不同的角度思考问题,优化解决问题的方法。(难点)
学习目标
喜欢打电话的同学可能会遇到下面这种问题,如:
1)还没到月底的时候免费的通话分钟数没有了。
2)月末的时候考虑我该换什么样的套餐合适呢?
两种电话计费方式表
套餐名称
A
B
月租费
50元/月
0
本地通话费
0.2元/分
0.6元/分
【问题一】思考A、B套餐可能出现月扣费的费用相同的情况吗?
设通话分钟数为m
50+0.2m=0+0.6m
解得 m=125分
当本月通话分钟为125分钟时,A、B套餐扣费相同
新课导入
喜欢打电话的同学可能会遇到下面这种问题,如:
1)还没到月底的时候免费的通话分钟数没有了。
2)月末的时候考虑我该换什么样的套餐合适呢?
两种电话计费方式表
套餐名称
A
B
月租费
50元/月
0
本地通话费
0.2元/分
0.6元/分
【问题二】若本月通话分钟数是50分和200分,你觉得用哪种套餐比较划算呢?
若通话分钟为50分钟
套餐A费用=50+50×0.2=60元
套餐B费用=0+50×0.6=30元
套餐B划算
若通话分钟为200分钟
套餐A费用=50+200×0.2=90元
套餐B费用=0+200×0.6=120元
套餐A划算
探究新知
喜欢打电话的同学可能会遇到下面这种问题,如:
1)还没到月底的时候免费的通话分钟数没有了。
2)月末的时候考虑我该换什么样的套餐合适呢?
两种电话计费方式表
套餐名称
A
B
月租费
50元/月
0
本地通话费
0.2元/分
0.6元/分
【问题三】若本月通话分钟数是x分,你觉得用哪种套餐比较划算呢?
若通话分钟为x分钟
套餐A费用=50+x×0.2=(50+0.2x)元
套餐B费用=0+x×0.6=0.6x元
1)当A套餐费用大于B套餐费用时,即
50+0.2x>0.6x,解得x<125
所以当x<125分钟时,B套餐所花费用少,B套餐划算
2)当A套餐费用小于B套餐费用时,即
50+0.2x<0.6x,解得x>125
所以当x>125分钟时,A套餐所花费用少,A套餐划算
3)同理,当x=125分钟时,A、B套餐所花费用相等
探究新知
{BDBED569-4797-4DF1-A0F4-6AAB3CD982D8}收费方式
月使用费/元
包时上网时间/h
超时费/(元/min)
A
30
25
0.05
B
50
50
0.05
C
120
不限时
选择哪种方式能节省上网费?
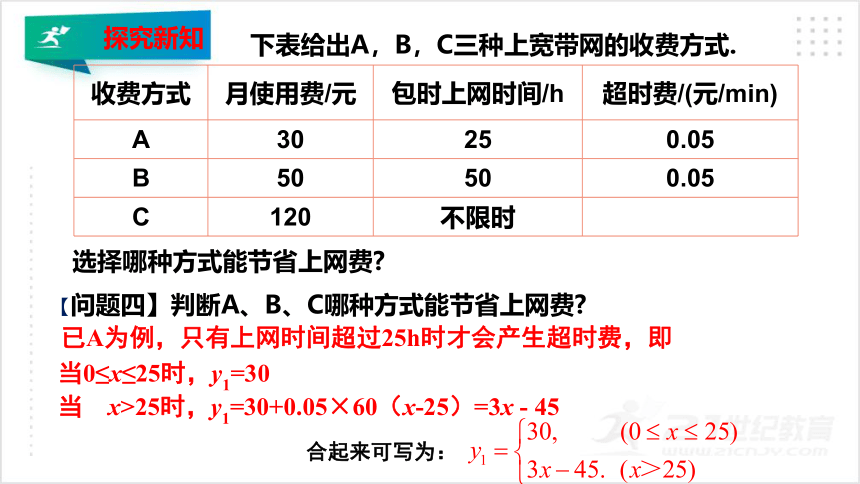
下表给出A,B,C三种上宽带网的收费方式.
【问题一】观察A、B、C三种收费方式,哪种收费方式是变化的?哪种不变?
【问题二】在变化的收费方式中,上网费由哪些部分组成?
【问题三】影响超时费的变量是什么?
A、B会变化,C不变
上网费=月使用费+超时费
上网时间
探究新知
选择哪种方式能节省上网费?
【问题四】判断A、B、C哪种方式能节省上网费?
设月上网时间为x,则方式A、B的上网费y1、y2都是x的函数,
要比较它们,需在 x > 0 时,考虑何时
(1) y1 = y2; (2) y1 < y2; (3) y1 > y2.
{BDBED569-4797-4DF1-A0F4-6AAB3CD982D8}收费方式
月使用费/元
包时上网时间/h
超时费/(元/min)
A
30
25
0.05
B
50
50
0.05
C
120
不限时
下表给出A,B,C三种上宽带网的收费方式.
探究新知
选择哪种方式能节省上网费?
【问题四】判断A、B、C哪种方式能节省上网费?
已A为例,只有上网时间超过25h时才会产生超时费,即
当0≤x≤25时,y1=30
当 x>25时,y1=30+0.05×60(x-25)=3x - 45
合起来可写为:
{BDBED569-4797-4DF1-A0F4-6AAB3CD982D8}收费方式
月使用费/元
包时上网时间/h
超时费/(元/min)
A
30
25
0.05
B
50
50
0.05
C
120
不限时
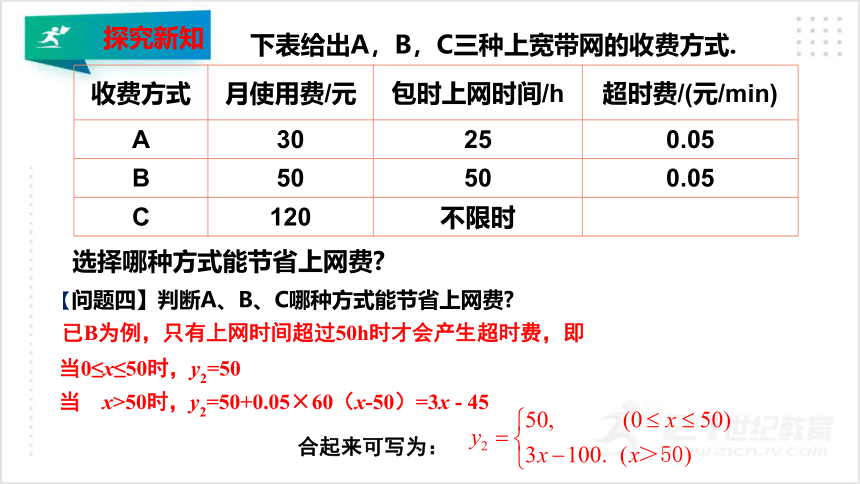
下表给出A,B,C三种上宽带网的收费方式.
探究新知
【问题四】判断A、B、C哪种方式能节省上网费?
已B为例,只有上网时间超过50h时才会产生超时费,即
当0≤x≤50时,y2=50
当 x>50时,y2=50+0.05×60(x-50)=3x - 45
合起来可写为:
{BDBED569-4797-4DF1-A0F4-6AAB3CD982D8}收费方式
月使用费/元
包时上网时间/h
超时费/(元/min)
A
30
25
0.05
B
50
50
0.05
C
120
不限时
下表给出A,B,C三种上宽带网的收费方式.
探究新知
选择哪种方式能节省上网费?
【问题四】判断A、B、C哪种方式能节省上网费?
已C为例,上网费是一个定值,即当x≥0时,y3=120
{BDBED569-4797-4DF1-A0F4-6AAB3CD982D8}收费方式
月使用费/元
包时上网时间/h
超时费/(元/min)
A
30
25
0.05
B
50
50
0.05
C
120
不限时
下表给出A,B,C三种上宽带网的收费方式.
探究新知
选择哪种方式能节省上网费?
y3=120 (x≥0)
你能在同一直角坐标系中画出它们的图象吗?
探究新知
在此区间,方式A划算
从函数图象中,可得知
1)当上网时间__________时,选择方式A最省钱.
2)当上网时间_________ _时,选择方式B最省钱.
3)当上网时间__________时,选择方式C最省钱.
3x – 45<50,解得x?
0?
????????????????
?
在此区间,方式B划算
3x – 100<120,解得x?
????????????????
?
??????????????????
x>????????????????
?
在此区间,方式C划算
探究新知
某学校计划在总费用2300元的限额内,租用汽车送234名学生和6名教师集体外出活动,每辆汽车上至少有1名教师.现有甲、乙两种大客车,它们的载客量和租金如表所示:
甲种客车
乙种客车
载客量(单位:人/辆)
45
30
租金 (单位:元/辆)
400
280
【问题一】有几种租车方案?
1)只租甲钟客车 2)只租乙种客车 3)甲乙混租
【问题二】根据题干内容,所租汽车需要满足什么条件吗?
1)所花费用不超过2300元
2)所租汽车数量可以满足240名师生都有车坐
3)每辆汽车上至少有1名教师
【问题三】根据条件二、条件三,你能确定租车数量吗?
根据条件二:只租甲钟客车需要240÷45= 513 辆
只租乙种客车需要240÷30=8 辆
即租车总数不能小于6辆,不能大于8辆
?
根据条件三:车辆总数不能超过6辆,因此可以排除只租
乙种客车方案。
综上所述:车辆总数只能为6辆
探究新知
某学校计划在总费用2300元的限额内,租用汽车送234名学生和6名教师集体外出活动,每辆汽车上至少有1名教师.现有甲、乙两种大客车,它们的载客量和租金如表所示:
甲种客车
乙种客车
载客量(单位:人/辆)
45
30
租金 (单位:元/辆)
400
280
【问题四】若甲、乙客车混租,你能确定租车方案吗?
设租用x辆甲种客车,则租车费用y(单位:元)是x的函数,即y=400x+280(6-x),化简这个函数,得y=120x+1680
1)为使240名师生有车坐,可以确定x的一个范围吗?
2)为使租车费用不超过2300元,又可以确定x的范围吗?
探究新知
某学校计划在总费用2300元的限额内,租用汽车送234名学生和6名教师集体外出活动,每辆汽车上至少有1名教师.现有甲、乙两种大客车,它们的载客量和租金如表所示:
甲种客车
乙种客车
载客量(单位:人/辆)
45
30
租金 (单位:元/辆)
400
280
【问题四】若甲、乙客车混租,你能确定租车方案吗?
∵x是正整数 ∴x=4或5;
有两种租车方案:
方案一:租甲种客车4辆,乙种客车2辆
方案二:租甲种客车5辆,乙种客车1辆
∵120>0
∴y 随着 x 的增大而增大,
∴当 x=4时,y最小,y的最小值为2160.
答:为节省费用选择第一个方案租甲种客车4辆,乙种客车2辆.
探究新知
归纳小结
用数学方法选择方案一般可分为三步:
①构建函数模型,找出函数关系式;
②确定自变量的取值范围或是针对自变量的取值进行讨论;
③由函数的性质(或经过比较后)直接得出最佳方案.
1.在抗击新冠状病毒战斗中,有152箱公共卫生防护用品要运到????、????两城镇,若用大小货车共15辆,则恰好能一次性运完这批防护用品,已知这两种大小货车的载货能力分别为12箱/辆和8箱/辆,其中用大货车运往????、????两城镇的运费分别为每辆800元和900元,用小货车运往????、????两城镇的运费分别为每辆400元和600元.
【问题一】求这15辆车中大小货车各多少辆?
?
解:(1)设大货车用x辆,小货车用y辆,根据题意得:
????+????=????????????????????+????????=???????????? 解得:????=????????=????
答:大货车用8辆,小货车用7辆;
?
课堂练习
2.在抗击新冠状病毒战斗中,有152箱公共卫生防护用品要运到????、????两城镇,若用大小货车共15辆,则恰好能一次性运完这批防护用品,已知这两种大小货车的载货能力分别为12箱/辆和8箱/辆,其中用大货车运往????、????两城镇的运费分别为每辆800元和900元,用小货车运往????、????两城镇的运费分别为每辆400元和600元.
【问题一】现安排其中10辆货车前往????城镇,其余货车前往????城镇,设前往????城镇的大货车为????辆,前往????、????两城镇总费用为????元,试求出????与????的函数解析式.若运往????城镇的防护用品不能少于100箱,请你写出符合要求的最少费用.
?
设前往A城镇的大货车为x辆,则前往B城镇的大货车为(8-x)辆,
前往A城镇的小货车为(10-x)辆,前往B城镇的小货车为[7-(10-x)]辆,
根据题意得:y=800x+900(8-x)+400(10-x)+600[7-(10-x)]=100x+9400
由运往????城镇的防护用品不能少于100箱,则12x+ 8 (10-x)≥100,解得x≥5且x为整数;
当x=5时,费用最低,则:100×5+9400=9900元.
答:????与????的函数解析式为y=100x+9400;当运往????城镇的防护用品不能少于100箱,最 低费用为9900元.
?
课堂练习
2.2020年新型冠状病毒肺炎疫情肆虐,红星社区为了提高社区居民的身体素质,鼓励居民在家锻炼,特采购了一批跳绳免费发放,已知2根幸福牌跳绳和1根平安牌跳绳共需31元,2根平安牌跳绳和3根幸福牌跳绳共需54元.
(1)求幸福牌跳绳和平安牌跳绳的单价;
(2)已知该社区需要采购两种品牌的跳绳共60根,且平安牌跳绳的数量不少于幸福牌跳绳数量的2倍,请设计出最省钱的购买方案,并说明理由.
1)设一根幸福牌跳绳售价是x元,一根平安牌跳绳的售价是y元,根据题意,得:
????????+????=????????????????+????????=????????,解得:????=????????=????????,
答:幸福牌跳绳的单价是8元,平安牌的跳绳单价是15元;
?
(2)设购进幸福牌跳绳m根,总费用为W元,
根据题意,得:W=8m+15(60-m)=-7m+900,
∵-7<0,∴W随m的增大而减小,
又∵2m≤60-m,解得:m≤20,
而m为正整数,
∴当m=20时,W最小=-7×20+900=760,此时60-20=40,
答:幸福牌买20根,平安牌的买40根时最省钱.
课堂练习
{7DF18680-E054-41AD-8BC1-D1AEF772440D}?
甲种客车
乙种客车
载客量(座/辆)
60
45
租金(元/辆)
550
450
3.某年级380名师生秋游,计划租用7辆客车,现有甲、乙两种型号客车,它们的载客量和租金如表.
1)设租用甲种客车x辆,租车总费用为y元.求出y(元)与x(辆)之间的函数表达式;
2)当甲种客车有多少辆时,能保障所有的师生能参加秋游且租车费用最少,最少费用是多少元.
解:1)由题意,得y=550x+450(7﹣x),化简得y=100x+3150,
即y(元)与x(辆)之间的函数表达式是y=100x+3150;
2)由题意得60x+45(7﹣x)≥380,解得,x≥????????????.
∵y=100x+3150,∴k=100>0,∴x=5时,租车费用最少,最少为:y=100×5+3150=3650(元),
即当甲种客车有5辆时,能保障所有的师生能参加秋游且租车费用最少,最少费用是3650元.
?
课堂练习
https://www.21cnjy.com/help/help_extract.php
第十九章 一次函数
2021年春人教版八年级(下)数学
1、会用一次函数知识解决方案选择问题,体会函数模型思想。
2、能从不同的角度思考问题,优化解决问题的方法。
如何用一次函数选择最佳方案。(重点)
能从不同的角度思考问题,优化解决问题的方法。(难点)
学习目标
喜欢打电话的同学可能会遇到下面这种问题,如:
1)还没到月底的时候免费的通话分钟数没有了。
2)月末的时候考虑我该换什么样的套餐合适呢?
两种电话计费方式表
套餐名称
A
B
月租费
50元/月
0
本地通话费
0.2元/分
0.6元/分
【问题一】思考A、B套餐可能出现月扣费的费用相同的情况吗?
设通话分钟数为m
50+0.2m=0+0.6m
解得 m=125分
当本月通话分钟为125分钟时,A、B套餐扣费相同
新课导入
喜欢打电话的同学可能会遇到下面这种问题,如:
1)还没到月底的时候免费的通话分钟数没有了。
2)月末的时候考虑我该换什么样的套餐合适呢?
两种电话计费方式表
套餐名称
A
B
月租费
50元/月
0
本地通话费
0.2元/分
0.6元/分
【问题二】若本月通话分钟数是50分和200分,你觉得用哪种套餐比较划算呢?
若通话分钟为50分钟
套餐A费用=50+50×0.2=60元
套餐B费用=0+50×0.6=30元
套餐B划算
若通话分钟为200分钟
套餐A费用=50+200×0.2=90元
套餐B费用=0+200×0.6=120元
套餐A划算
探究新知
喜欢打电话的同学可能会遇到下面这种问题,如:
1)还没到月底的时候免费的通话分钟数没有了。
2)月末的时候考虑我该换什么样的套餐合适呢?
两种电话计费方式表
套餐名称
A
B
月租费
50元/月
0
本地通话费
0.2元/分
0.6元/分
【问题三】若本月通话分钟数是x分,你觉得用哪种套餐比较划算呢?
若通话分钟为x分钟
套餐A费用=50+x×0.2=(50+0.2x)元
套餐B费用=0+x×0.6=0.6x元
1)当A套餐费用大于B套餐费用时,即
50+0.2x>0.6x,解得x<125
所以当x<125分钟时,B套餐所花费用少,B套餐划算
2)当A套餐费用小于B套餐费用时,即
50+0.2x<0.6x,解得x>125
所以当x>125分钟时,A套餐所花费用少,A套餐划算
3)同理,当x=125分钟时,A、B套餐所花费用相等
探究新知
{BDBED569-4797-4DF1-A0F4-6AAB3CD982D8}收费方式
月使用费/元
包时上网时间/h
超时费/(元/min)
A
30
25
0.05
B
50
50
0.05
C
120
不限时
选择哪种方式能节省上网费?
下表给出A,B,C三种上宽带网的收费方式.
【问题一】观察A、B、C三种收费方式,哪种收费方式是变化的?哪种不变?
【问题二】在变化的收费方式中,上网费由哪些部分组成?
【问题三】影响超时费的变量是什么?
A、B会变化,C不变
上网费=月使用费+超时费
上网时间
探究新知
选择哪种方式能节省上网费?
【问题四】判断A、B、C哪种方式能节省上网费?
设月上网时间为x,则方式A、B的上网费y1、y2都是x的函数,
要比较它们,需在 x > 0 时,考虑何时
(1) y1 = y2; (2) y1 < y2; (3) y1 > y2.
{BDBED569-4797-4DF1-A0F4-6AAB3CD982D8}收费方式
月使用费/元
包时上网时间/h
超时费/(元/min)
A
30
25
0.05
B
50
50
0.05
C
120
不限时
下表给出A,B,C三种上宽带网的收费方式.
探究新知
选择哪种方式能节省上网费?
【问题四】判断A、B、C哪种方式能节省上网费?
已A为例,只有上网时间超过25h时才会产生超时费,即
当0≤x≤25时,y1=30
当 x>25时,y1=30+0.05×60(x-25)=3x - 45
合起来可写为:
{BDBED569-4797-4DF1-A0F4-6AAB3CD982D8}收费方式
月使用费/元
包时上网时间/h
超时费/(元/min)
A
30
25
0.05
B
50
50
0.05
C
120
不限时
下表给出A,B,C三种上宽带网的收费方式.
探究新知
【问题四】判断A、B、C哪种方式能节省上网费?
已B为例,只有上网时间超过50h时才会产生超时费,即
当0≤x≤50时,y2=50
当 x>50时,y2=50+0.05×60(x-50)=3x - 45
合起来可写为:
{BDBED569-4797-4DF1-A0F4-6AAB3CD982D8}收费方式
月使用费/元
包时上网时间/h
超时费/(元/min)
A
30
25
0.05
B
50
50
0.05
C
120
不限时
下表给出A,B,C三种上宽带网的收费方式.
探究新知
选择哪种方式能节省上网费?
【问题四】判断A、B、C哪种方式能节省上网费?
已C为例,上网费是一个定值,即当x≥0时,y3=120
{BDBED569-4797-4DF1-A0F4-6AAB3CD982D8}收费方式
月使用费/元
包时上网时间/h
超时费/(元/min)
A
30
25
0.05
B
50
50
0.05
C
120
不限时
下表给出A,B,C三种上宽带网的收费方式.
探究新知
选择哪种方式能节省上网费?
y3=120 (x≥0)
你能在同一直角坐标系中画出它们的图象吗?
探究新知
在此区间,方式A划算
从函数图象中,可得知
1)当上网时间__________时,选择方式A最省钱.
2)当上网时间_________ _时,选择方式B最省钱.
3)当上网时间__________时,选择方式C最省钱.
3x – 45<50,解得x?
0
????????????????
?
在此区间,方式B划算
3x – 100<120,解得x?
????????????????
?
?????????????????
x>????????????????
?
在此区间,方式C划算
探究新知
某学校计划在总费用2300元的限额内,租用汽车送234名学生和6名教师集体外出活动,每辆汽车上至少有1名教师.现有甲、乙两种大客车,它们的载客量和租金如表所示:
甲种客车
乙种客车
载客量(单位:人/辆)
45
30
租金 (单位:元/辆)
400
280
【问题一】有几种租车方案?
1)只租甲钟客车 2)只租乙种客车 3)甲乙混租
【问题二】根据题干内容,所租汽车需要满足什么条件吗?
1)所花费用不超过2300元
2)所租汽车数量可以满足240名师生都有车坐
3)每辆汽车上至少有1名教师
【问题三】根据条件二、条件三,你能确定租车数量吗?
根据条件二:只租甲钟客车需要240÷45= 513 辆
只租乙种客车需要240÷30=8 辆
即租车总数不能小于6辆,不能大于8辆
?
根据条件三:车辆总数不能超过6辆,因此可以排除只租
乙种客车方案。
综上所述:车辆总数只能为6辆
探究新知
某学校计划在总费用2300元的限额内,租用汽车送234名学生和6名教师集体外出活动,每辆汽车上至少有1名教师.现有甲、乙两种大客车,它们的载客量和租金如表所示:
甲种客车
乙种客车
载客量(单位:人/辆)
45
30
租金 (单位:元/辆)
400
280
【问题四】若甲、乙客车混租,你能确定租车方案吗?
设租用x辆甲种客车,则租车费用y(单位:元)是x的函数,即y=400x+280(6-x),化简这个函数,得y=120x+1680
1)为使240名师生有车坐,可以确定x的一个范围吗?
2)为使租车费用不超过2300元,又可以确定x的范围吗?
探究新知
某学校计划在总费用2300元的限额内,租用汽车送234名学生和6名教师集体外出活动,每辆汽车上至少有1名教师.现有甲、乙两种大客车,它们的载客量和租金如表所示:
甲种客车
乙种客车
载客量(单位:人/辆)
45
30
租金 (单位:元/辆)
400
280
【问题四】若甲、乙客车混租,你能确定租车方案吗?
∵x是正整数 ∴x=4或5;
有两种租车方案:
方案一:租甲种客车4辆,乙种客车2辆
方案二:租甲种客车5辆,乙种客车1辆
∵120>0
∴y 随着 x 的增大而增大,
∴当 x=4时,y最小,y的最小值为2160.
答:为节省费用选择第一个方案租甲种客车4辆,乙种客车2辆.
探究新知
归纳小结
用数学方法选择方案一般可分为三步:
①构建函数模型,找出函数关系式;
②确定自变量的取值范围或是针对自变量的取值进行讨论;
③由函数的性质(或经过比较后)直接得出最佳方案.
1.在抗击新冠状病毒战斗中,有152箱公共卫生防护用品要运到????、????两城镇,若用大小货车共15辆,则恰好能一次性运完这批防护用品,已知这两种大小货车的载货能力分别为12箱/辆和8箱/辆,其中用大货车运往????、????两城镇的运费分别为每辆800元和900元,用小货车运往????、????两城镇的运费分别为每辆400元和600元.
【问题一】求这15辆车中大小货车各多少辆?
?
解:(1)设大货车用x辆,小货车用y辆,根据题意得:
????+????=????????????????????+????????=???????????? 解得:????=????????=????
答:大货车用8辆,小货车用7辆;
?
课堂练习
2.在抗击新冠状病毒战斗中,有152箱公共卫生防护用品要运到????、????两城镇,若用大小货车共15辆,则恰好能一次性运完这批防护用品,已知这两种大小货车的载货能力分别为12箱/辆和8箱/辆,其中用大货车运往????、????两城镇的运费分别为每辆800元和900元,用小货车运往????、????两城镇的运费分别为每辆400元和600元.
【问题一】现安排其中10辆货车前往????城镇,其余货车前往????城镇,设前往????城镇的大货车为????辆,前往????、????两城镇总费用为????元,试求出????与????的函数解析式.若运往????城镇的防护用品不能少于100箱,请你写出符合要求的最少费用.
?
设前往A城镇的大货车为x辆,则前往B城镇的大货车为(8-x)辆,
前往A城镇的小货车为(10-x)辆,前往B城镇的小货车为[7-(10-x)]辆,
根据题意得:y=800x+900(8-x)+400(10-x)+600[7-(10-x)]=100x+9400
由运往????城镇的防护用品不能少于100箱,则12x+ 8 (10-x)≥100,解得x≥5且x为整数;
当x=5时,费用最低,则:100×5+9400=9900元.
答:????与????的函数解析式为y=100x+9400;当运往????城镇的防护用品不能少于100箱,最 低费用为9900元.
?
课堂练习
2.2020年新型冠状病毒肺炎疫情肆虐,红星社区为了提高社区居民的身体素质,鼓励居民在家锻炼,特采购了一批跳绳免费发放,已知2根幸福牌跳绳和1根平安牌跳绳共需31元,2根平安牌跳绳和3根幸福牌跳绳共需54元.
(1)求幸福牌跳绳和平安牌跳绳的单价;
(2)已知该社区需要采购两种品牌的跳绳共60根,且平安牌跳绳的数量不少于幸福牌跳绳数量的2倍,请设计出最省钱的购买方案,并说明理由.
1)设一根幸福牌跳绳售价是x元,一根平安牌跳绳的售价是y元,根据题意,得:
????????+????=????????????????+????????=????????,解得:????=????????=????????,
答:幸福牌跳绳的单价是8元,平安牌的跳绳单价是15元;
?
(2)设购进幸福牌跳绳m根,总费用为W元,
根据题意,得:W=8m+15(60-m)=-7m+900,
∵-7<0,∴W随m的增大而减小,
又∵2m≤60-m,解得:m≤20,
而m为正整数,
∴当m=20时,W最小=-7×20+900=760,此时60-20=40,
答:幸福牌买20根,平安牌的买40根时最省钱.
课堂练习
{7DF18680-E054-41AD-8BC1-D1AEF772440D}?
甲种客车
乙种客车
载客量(座/辆)
60
45
租金(元/辆)
550
450
3.某年级380名师生秋游,计划租用7辆客车,现有甲、乙两种型号客车,它们的载客量和租金如表.
1)设租用甲种客车x辆,租车总费用为y元.求出y(元)与x(辆)之间的函数表达式;
2)当甲种客车有多少辆时,能保障所有的师生能参加秋游且租车费用最少,最少费用是多少元.
解:1)由题意,得y=550x+450(7﹣x),化简得y=100x+3150,
即y(元)与x(辆)之间的函数表达式是y=100x+3150;
2)由题意得60x+45(7﹣x)≥380,解得,x≥????????????.
∵y=100x+3150,∴k=100>0,∴x=5时,租车费用最少,最少为:y=100×5+3150=3650(元),
即当甲种客车有5辆时,能保障所有的师生能参加秋游且租车费用最少,最少费用是3650元.
?
课堂练习
https://www.21cnjy.com/help/help_extract.php
