多边形的内角和 导学案

《多边形的内角和》导学案设计
《多边形的内角和》导学案设计 姓名：
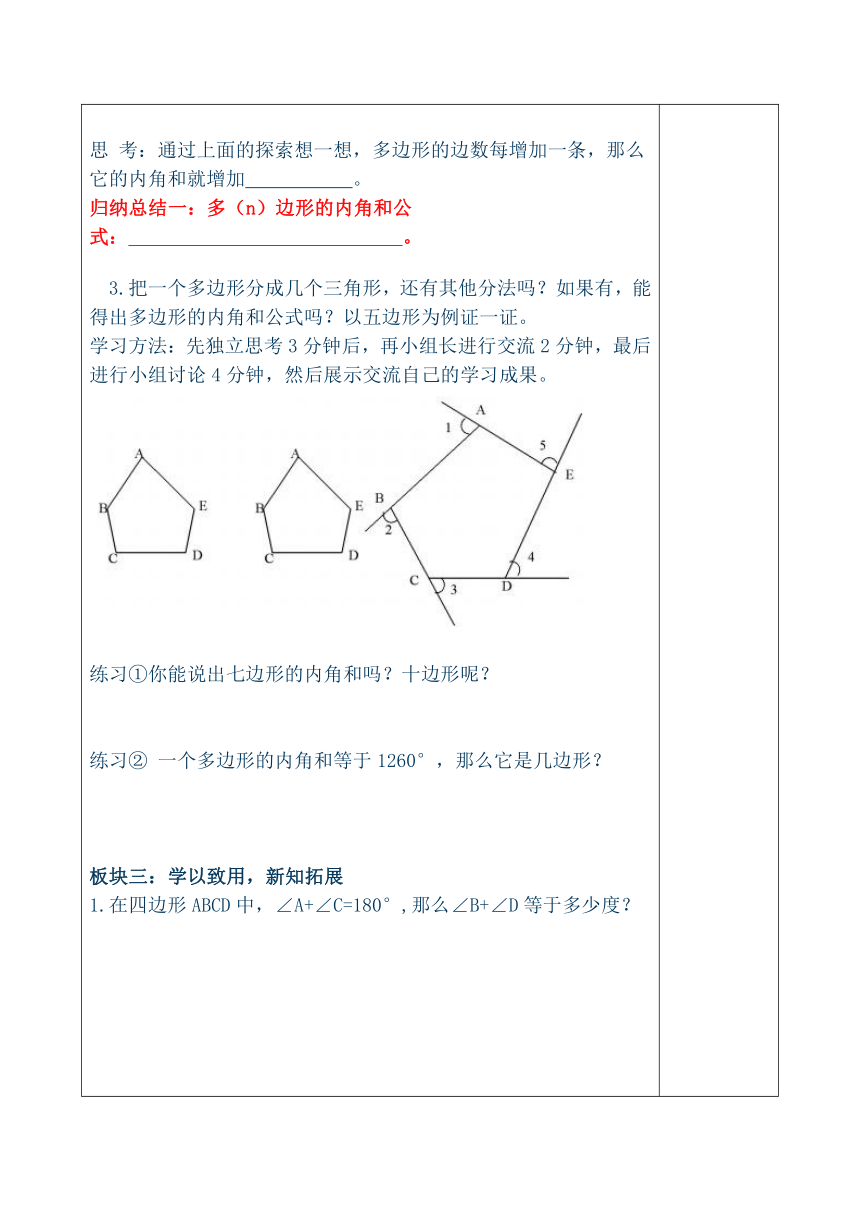
学习目标:1.探索多边形的内角和公式及外角和。2.会利用多边形的内角和公式解决问题。学习重点：掌握多边形的内角和公式。学习难点：探索多边形的内角和公式。学习用具：三角尺导学过程：板块一：温故知新1.多边形： 。2.三角形的内角和等于 ,外角和等于 。3.长方形的内角和等于 ,外角和等于 。4.从六边形的一个顶点出发可以画 条对角线，这些对角线将六边形分成 个三角形。 板块二：探究新知1.任意四边形的内角和等于多少度？你是怎样得到的？学习方法：独立思考1分钟后小组内交流答案。2.探索同一种方法分别求出任意五边形、六边形的内角和等于多少度？学习方法：先独立思考2分钟，再小组进行讨论2分钟；看哪个小组即对又快。 思 考：通过上面的探索想一想，多边形的边数每增加一条，那么它的内角和就增加 。归纳总结一：多（n）边形的内角和公式： 。 3.把一个多边形分成几个三角形，还有其他分法吗？如果有，能得出多边形的内角和公式吗？以五边形为例证一证。学习方法：先独立思考3分钟后，再小组长进行交流2分钟，最后进行小组讨论4分钟，然后展示交流自己的学习成果。练习①你能说出七边形的内角和吗？十边形呢？ 练习② 一个多边形的内角和等于1260°，那么它是几边形？ 板块三：学以致用，新知拓展1.在四边形ABCD中，∠A+∠C=180°,那么∠B+∠D等于多少度？ 2.根据前面三角形的有关知识，探索在每个五边形顶点处各取一个外角，这些外角的和叫做五边形的外角和，请探究：（1）五边形的外角和等于多少度？（2）类似六边形的外角和是多少度？ 归纳总结二：多(n)边形的外角和是： 。板块四：收获交流请梳理一下，本节课你学到了哪些新知识？还有什么疑问需要交流？ 板块五：展示平台〈1〉基础巩固①求下列图形中的x值②一个多边形的内角和等于1800°，则它的边数为 条。③已知四边形ABCD中，∠A∶∠B∶∠C ∶∠D=1∶2∶3∶4，则∠C= 。④一个多边形的每个内角都等于150°，则它的边数为 条。⑤正10边形的每个内角都等于 。⑥如图，四边形ABCD中，∠A=∠C, ∠B=∠D,AB与CD有什么关系？请说明理由。 〈2〉创新思维为了迎接2012年的到来，楠楠同学想设计一个内角和是2012°的多边形图案，他的想法能实现吗？试说明理由。 〈3〉中考链接①若正多边形的一个外角是30°，则这是 边形。②如图所示，小亮从A点出发前进10m，向右转15°，再前进10m，又向右转15°，……，这样一直走下去，他第一次回到出发点A时，一共走了 m。 编号：
日期：
师生体会
教师评议
学案等级：