2020-2021学年人教版数学八年级下册 19.2.2.2 正比例函数的图象和性质 课件(共32张ppt)
文档属性
| 名称 | 2020-2021学年人教版数学八年级下册 19.2.2.2 正比例函数的图象和性质 课件(共32张ppt) |

|
|
| 格式 | ppt | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-04-19 12:06:15 | ||
图片预览





文档简介
(共32张PPT)
第十九章
一次函数
19.2.1正比例函数的图像和性质
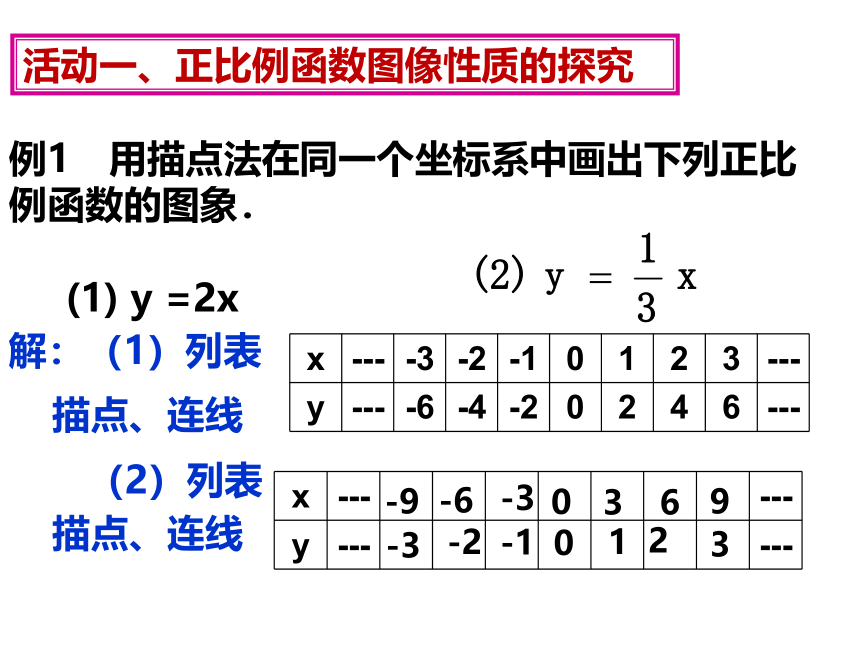
例1 用描点法在同一个坐标系中画出下列正比例函数的图象.
(1)
y
=2x
活动一、正比例函数图像性质的探究
x
---
-3
-2
-1
0
1
2
3
---
y
---
-6
-4
-2
0
2
4
6
---
解:(1)列表
(2)列表
x
---
---
y
---
---
描点、连线
描点、连线
3
0
0
9
-3
-6
-9
1
2
3
-1
-2
-3
6
y
=2x
6
4
2
-2
6
x
y
O
4
2
-4
-2
y
=x
y
=4x
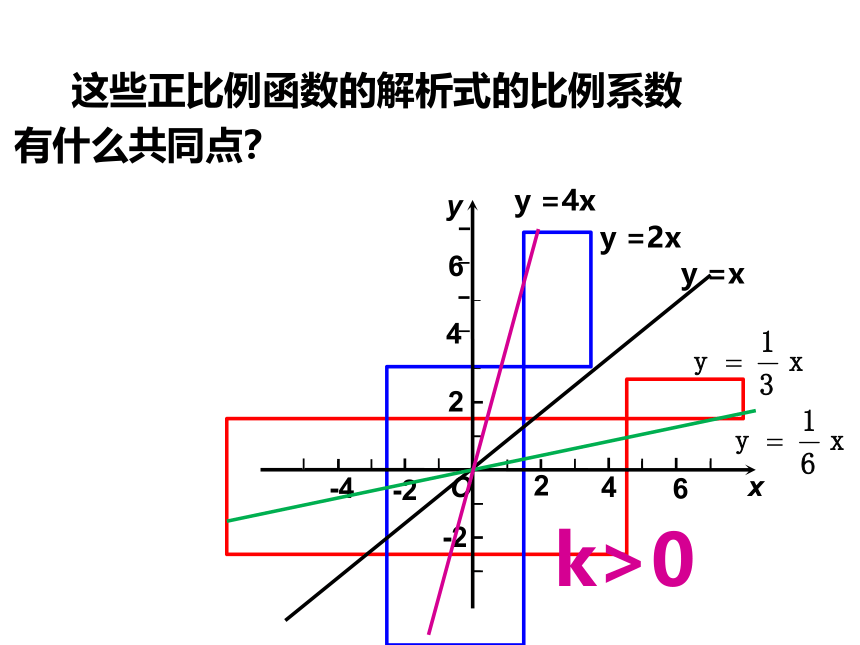
这些正比例函数的解析式的比例系数
有什么共同点?
k>0
y
=2x
6
4
2
-2
6
x
y
O
4
2
-4
-2
y
=x
y
=4x
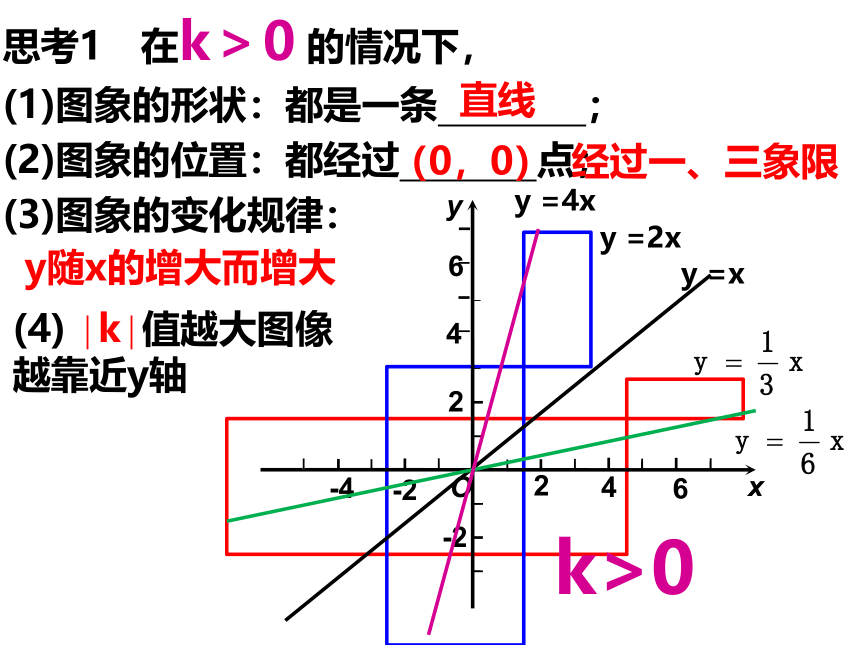
思考1 在k>0
的情况下,
(1)图象的形状:都是一条
;
(2)图象的位置:都经过
点;
(3)图象的变化规律:
直线
(0,0)
y随x的增大而增大
经过一、三象限
k>0
(4)
∣k∣值越大图像越靠近y轴
例2 用描点法画出正比例函数的图象.
(1)
y
=-2x;
x
---
-3
-2
-1
0
1
2
3
---
y
---
6
4
2
0
-2
-4
-6
---
解:(1)列表
(2)列表
x
---
---
y
---
---
描点、连线
描点、连线
3
0
0
9
-3
-6
-9
-1
-2
-3
1
2
3
6
y
=-2x
6
4
2
-2
6
x
y
O
4
2
-4
-2
y
=-x
y
=-4x
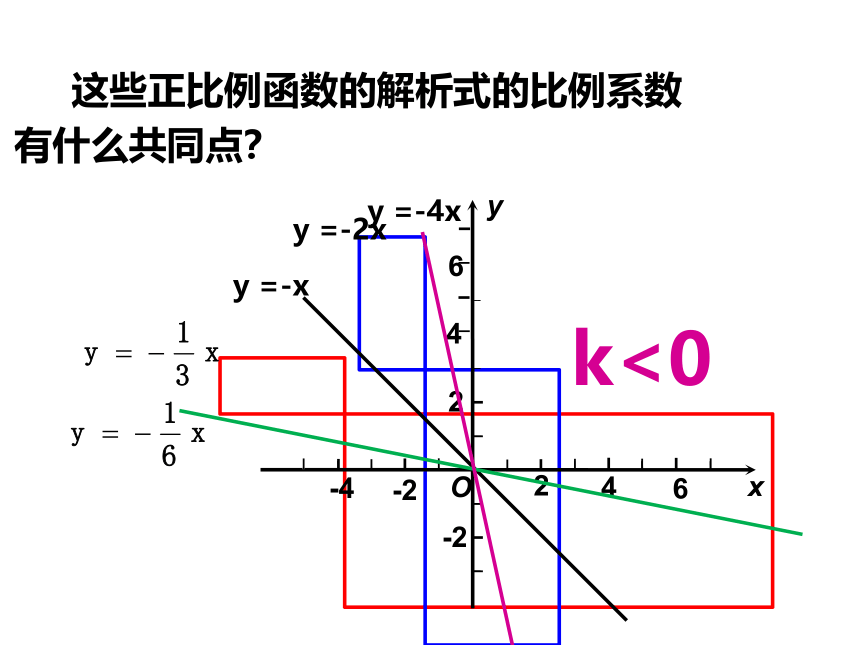
这些正比例函数的解析式的比例系数
有什么共同点?
k<0
解析式
y
=
kx
(k>0)
y
=
kx
(k<0)
图
象
图象位置
变化规律
结论1、正比例函数y=
kx
(k≠0)
的图象
是经过原点(0,0)
的一条直线。
第一、三象限
第二、四象限
y随着x的增大而增大
y随着x的增
大而减少
0
x
y
0
x
y
结论2、正比例函数y=
kx
(k≠0)
的性质
和点(1,k)
它经过第
象限,
直线
二、四
减小
一、三
0
7
象限内,经过点(0,
)与
1、函数
y
=7x
的图象在第
点(1,
),y随x的增大而
增大
2、正比例函数
的图象
是经过点(
)和(
)的一条
,
0,0
1,
-5
y
随着
x
的增大而
活动二、随堂练习
3、用你认为最简单的方法在同一坐标系中
画出画出下列函数的图象:
(1)
; (2)
y
=-3x.
0
x
y
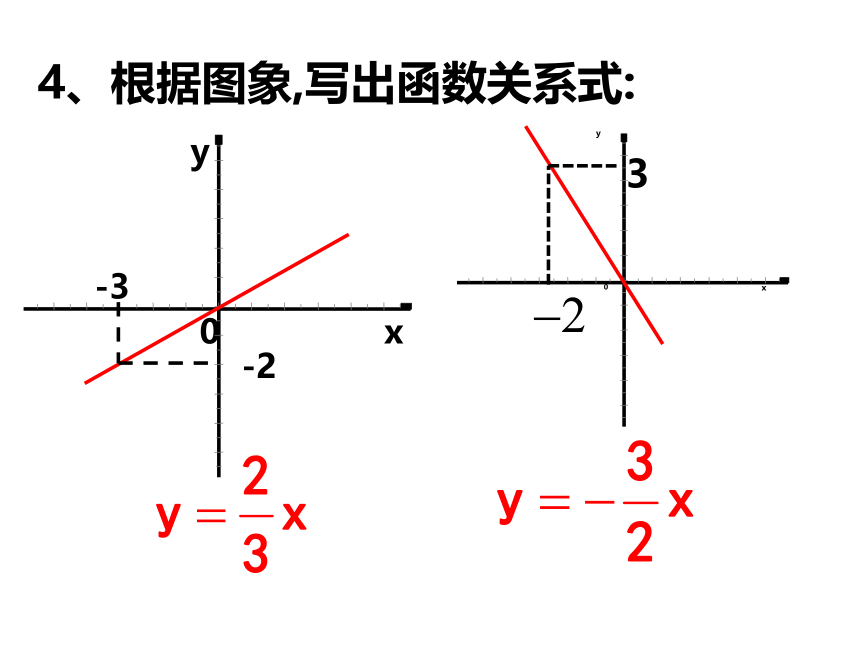
4、根据图象,写出函数关系式:
3
0
x
y
-2
-3
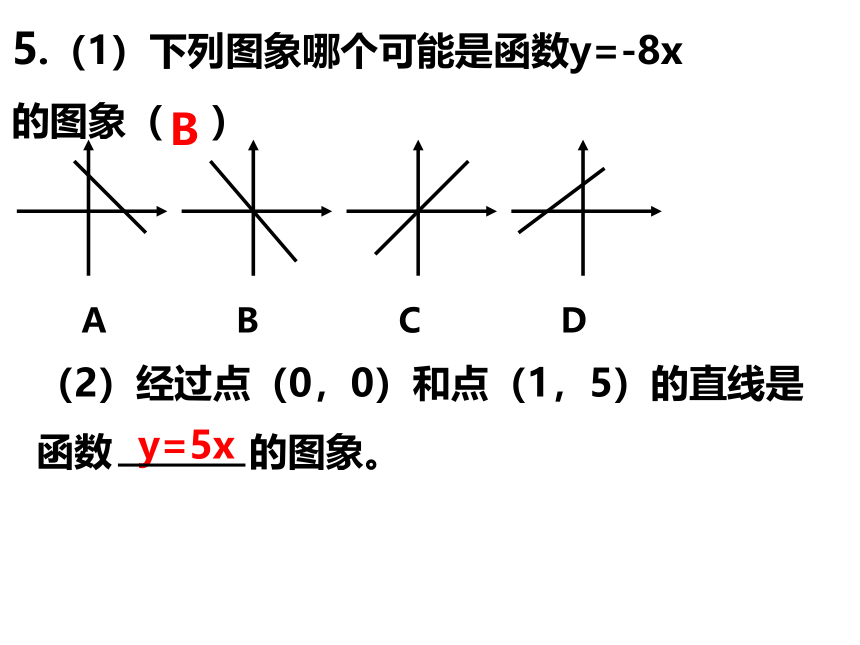
B
5.(1)下列图象哪个可能是函数y=-8x
的图象(
)
A
B
C
D
y=5x
(2)经过点(0,0)和点(1,5)的直线是
函数
的图象。
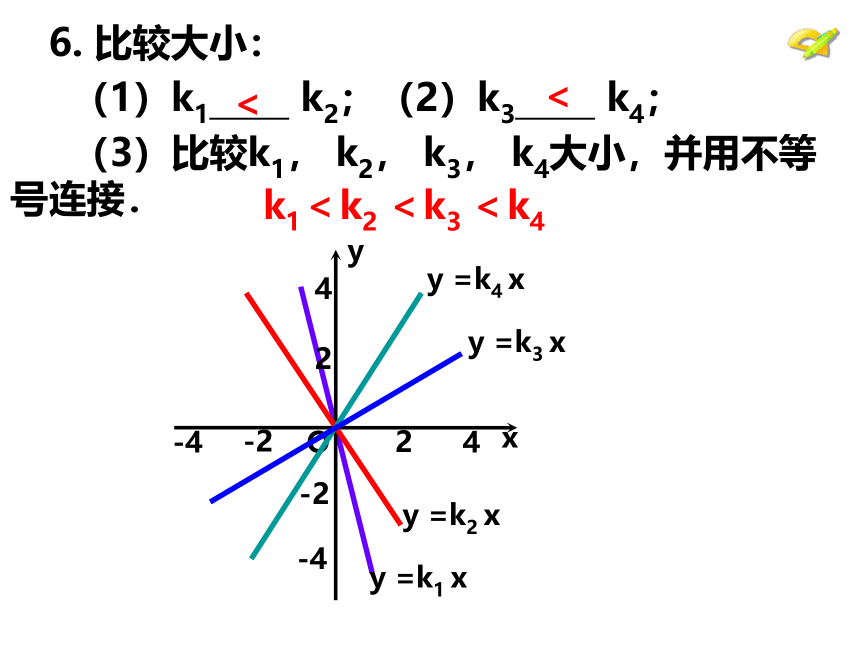
6.
比较大小:
(1)k1
k2;(2)k3
k4;
(3)比较k1,
k2,
k3,
k4大小,并用不等号连接.
<
k1<k2
<k3
<k4
4
2
-2
-4
4
x
y
O
y
=k4
x
-4
-2
2
y
=k3
x
y
=k2
x
y
=k1
x
<
7、如果
是正比例函数,
且y随x的增大而减小,那么m=
。
D
D
10、
有一长为16米的绳子,现用它围成正方形
场地,绳子可以不用完。设正方形的边长为x,
周长为y.
(1)求y与x的函数关系式,
并求自变量x的取值范围;
(2)画出函数的图像;
(3)要使所围成的正方形面积为9m2,求周长.
y=4x
0取(0,0)
和(4,16)
滑车以每分15米的速度匀速地从
轨道的一端
滑向另一端,已知轨道
的长为7米。
(1)求滑车滑行的路程
S(米)和滑行时间t(分)之间的关系式和自变量t的取值范围;
(2)画出图象;
(3)根据图象说明当
t
增大时,
S随着增大还是减少?
9、在同一坐标系里画出下列函数的图象
观察所得的两个函数图象说明:
(1)当x
______时,y1=y2;当x
______时,y1>y2;
当x______时,y1(2)过点A(0,2)做y轴的垂线,与两直线分别交于
点B,C,求S⊿OBC.
=0
>0
<0
0
x
y
-6
-4
-2
0
2
4
6
x
y=2x
x
…
-3
-2
-1
0
1
2
3
…
y
…
…
x
-5
-4
-3
-2
-1
5
4
3
2
1
-1
0
-2
-3
-4
-5
1
2
3
4
5
x
y
-5
-4
-3
-2
-1
5
4
3
2
1
-1
0
-2
-3
-4
-5
1
2
3
4
5
x
y
y=-2x
x
…
-3
-2
-1
0
1
2
3
…
y
…
…
6
4
2
0
-2
-4
-6
-5
-4
-3
-2
-1
5
4
3
2
1
-1
0
-2
-3
-4
-5
1
2
3
4
5
x
y
y=2x
y=-2x
两个正比例函数图像有何共同特点?
x
y
-5
-4
-3
-2
-1
5
4
3
2
1
-1
0
-2
-3
-4
-5
1
2
3
4
5
例2(1)画函数
y=
x
,
y=
x的图象
y=
x
(1,1)
(2,1)
y=2x
有
哪
些
共
同
的
特
点?
x
y
-3
-2
-1
5
4
3
2
1
-2
-3
-4
-5
1
2
3
4
5
例2:画函数
y=
-x
,
的图象
●
●
y=
-x
y=-2x
有哪些共同的特点?
活动三
小组讨论与归纳
相同点?
不同点?
x
y
0
1
1
-2
-1
2
-2
-1
2
y=
x
解析式
y
=
kx
(k>0)
y
=
kx
(k<0)
图
象
图象位置
函数变化
结论1、正比例函数y=
kx
(k≠0)
的图象是
经过原点(0,0)和点(1,k)的一条直线。
第一、三象限
第二、四象限
y随着x的增大
而增大
y随着x的增大
而减少
0
x
y
0
x
y
结论2、正比例函数y=
kx
(k≠0)
的性质
x
y
0
1
1
-2
-1
2
-2
-1
2
y=
x
结论3、当
|k|
越大时,图象越靠近y轴
活动四
我
练
我
进
步
练习2 在平面直角坐标系中,正比例函数y
=kx(
k<0)的图象的大致位置只可能是( ).
x
y
O
x
y
O
x
y
O
x
y
O
A
B
C
D
A
练习
练习3 对于正比例函数y
=kx,当x
增大时,y
随x
的增大而增大,则k的取值范围
(
).
A.k<0 B.k≤0
C.k>0 D.k≥0
C
练习
练习4
比较大小:
(1)k1
k2;(2)k3
k4;
(3)比较k1,
k2,
k3,
k4大小,并用不等号连接.
<
k1<k2
<k3
<k4
练习
4
2
-2
-4
4
x
y
O
y
=k4
x
-4
-2
2
y
=k3
x
y
=k2
x
y
=k1
x
<
小结 对一般正比例函数y
=kx,
当k>0时,
(1)它的图象形状?
(2)位置怎样?
(3)图象的变化规律?
是一条直线
经过一、三象限
y随x的增大而增大
例2 用描点法画出正比例函数
(1)
y
=-2x;
的图象.
思考2 当k<0时,
(1)它的图象形状?
(2)位置怎样?
(3)图象的变化规律?
是一条直线
经过二、四象限
y随x的增大而减少
(0,0)点;
(4)
∣k∣值越大图像越靠近y轴
第十九章
一次函数
19.2.1正比例函数的图像和性质
例1 用描点法在同一个坐标系中画出下列正比例函数的图象.
(1)
y
=2x
活动一、正比例函数图像性质的探究
x
---
-3
-2
-1
0
1
2
3
---
y
---
-6
-4
-2
0
2
4
6
---
解:(1)列表
(2)列表
x
---
---
y
---
---
描点、连线
描点、连线
3
0
0
9
-3
-6
-9
1
2
3
-1
-2
-3
6
y
=2x
6
4
2
-2
6
x
y
O
4
2
-4
-2
y
=x
y
=4x
这些正比例函数的解析式的比例系数
有什么共同点?
k>0
y
=2x
6
4
2
-2
6
x
y
O
4
2
-4
-2
y
=x
y
=4x
思考1 在k>0
的情况下,
(1)图象的形状:都是一条
;
(2)图象的位置:都经过
点;
(3)图象的变化规律:
直线
(0,0)
y随x的增大而增大
经过一、三象限
k>0
(4)
∣k∣值越大图像越靠近y轴
例2 用描点法画出正比例函数的图象.
(1)
y
=-2x;
x
---
-3
-2
-1
0
1
2
3
---
y
---
6
4
2
0
-2
-4
-6
---
解:(1)列表
(2)列表
x
---
---
y
---
---
描点、连线
描点、连线
3
0
0
9
-3
-6
-9
-1
-2
-3
1
2
3
6
y
=-2x
6
4
2
-2
6
x
y
O
4
2
-4
-2
y
=-x
y
=-4x
这些正比例函数的解析式的比例系数
有什么共同点?
k<0
解析式
y
=
kx
(k>0)
y
=
kx
(k<0)
图
象
图象位置
变化规律
结论1、正比例函数y=
kx
(k≠0)
的图象
是经过原点(0,0)
的一条直线。
第一、三象限
第二、四象限
y随着x的增大而增大
y随着x的增
大而减少
0
x
y
0
x
y
结论2、正比例函数y=
kx
(k≠0)
的性质
和点(1,k)
它经过第
象限,
直线
二、四
减小
一、三
0
7
象限内,经过点(0,
)与
1、函数
y
=7x
的图象在第
点(1,
),y随x的增大而
增大
2、正比例函数
的图象
是经过点(
)和(
)的一条
,
0,0
1,
-5
y
随着
x
的增大而
活动二、随堂练习
3、用你认为最简单的方法在同一坐标系中
画出画出下列函数的图象:
(1)
; (2)
y
=-3x.
0
x
y
4、根据图象,写出函数关系式:
3
0
x
y
-2
-3
B
5.(1)下列图象哪个可能是函数y=-8x
的图象(
)
A
B
C
D
y=5x
(2)经过点(0,0)和点(1,5)的直线是
函数
的图象。
6.
比较大小:
(1)k1
k2;(2)k3
k4;
(3)比较k1,
k2,
k3,
k4大小,并用不等号连接.
<
k1<k2
<k3
<k4
4
2
-2
-4
4
x
y
O
y
=k4
x
-4
-2
2
y
=k3
x
y
=k2
x
y
=k1
x
<
7、如果
是正比例函数,
且y随x的增大而减小,那么m=
。
D
D
10、
有一长为16米的绳子,现用它围成正方形
场地,绳子可以不用完。设正方形的边长为x,
周长为y.
(1)求y与x的函数关系式,
并求自变量x的取值范围;
(2)画出函数的图像;
(3)要使所围成的正方形面积为9m2,求周长.
y=4x
0
和(4,16)
滑车以每分15米的速度匀速地从
轨道的一端
滑向另一端,已知轨道
的长为7米。
(1)求滑车滑行的路程
S(米)和滑行时间t(分)之间的关系式和自变量t的取值范围;
(2)画出图象;
(3)根据图象说明当
t
增大时,
S随着增大还是减少?
9、在同一坐标系里画出下列函数的图象
观察所得的两个函数图象说明:
(1)当x
______时,y1=y2;当x
______时,y1>y2;
当x______时,y1
点B,C,求S⊿OBC.
=0
>0
<0
0
x
y
-6
-4
-2
0
2
4
6
x
y=2x
x
…
-3
-2
-1
0
1
2
3
…
y
…
…
x
-5
-4
-3
-2
-1
5
4
3
2
1
-1
0
-2
-3
-4
-5
1
2
3
4
5
x
y
-5
-4
-3
-2
-1
5
4
3
2
1
-1
0
-2
-3
-4
-5
1
2
3
4
5
x
y
y=-2x
x
…
-3
-2
-1
0
1
2
3
…
y
…
…
6
4
2
0
-2
-4
-6
-5
-4
-3
-2
-1
5
4
3
2
1
-1
0
-2
-3
-4
-5
1
2
3
4
5
x
y
y=2x
y=-2x
两个正比例函数图像有何共同特点?
x
y
-5
-4
-3
-2
-1
5
4
3
2
1
-1
0
-2
-3
-4
-5
1
2
3
4
5
例2(1)画函数
y=
x
,
y=
x的图象
y=
x
(1,1)
(2,1)
y=2x
有
哪
些
共
同
的
特
点?
x
y
-3
-2
-1
5
4
3
2
1
-2
-3
-4
-5
1
2
3
4
5
例2:画函数
y=
-x
,
的图象
●
●
y=
-x
y=-2x
有哪些共同的特点?
活动三
小组讨论与归纳
相同点?
不同点?
x
y
0
1
1
-2
-1
2
-2
-1
2
y=
x
解析式
y
=
kx
(k>0)
y
=
kx
(k<0)
图
象
图象位置
函数变化
结论1、正比例函数y=
kx
(k≠0)
的图象是
经过原点(0,0)和点(1,k)的一条直线。
第一、三象限
第二、四象限
y随着x的增大
而增大
y随着x的增大
而减少
0
x
y
0
x
y
结论2、正比例函数y=
kx
(k≠0)
的性质
x
y
0
1
1
-2
-1
2
-2
-1
2
y=
x
结论3、当
|k|
越大时,图象越靠近y轴
活动四
我
练
我
进
步
练习2 在平面直角坐标系中,正比例函数y
=kx(
k<0)的图象的大致位置只可能是( ).
x
y
O
x
y
O
x
y
O
x
y
O
A
B
C
D
A
练习
练习3 对于正比例函数y
=kx,当x
增大时,y
随x
的增大而增大,则k的取值范围
(
).
A.k<0 B.k≤0
C.k>0 D.k≥0
C
练习
练习4
比较大小:
(1)k1
k2;(2)k3
k4;
(3)比较k1,
k2,
k3,
k4大小,并用不等号连接.
<
k1<k2
<k3
<k4
练习
4
2
-2
-4
4
x
y
O
y
=k4
x
-4
-2
2
y
=k3
x
y
=k2
x
y
=k1
x
<
小结 对一般正比例函数y
=kx,
当k>0时,
(1)它的图象形状?
(2)位置怎样?
(3)图象的变化规律?
是一条直线
经过一、三象限
y随x的增大而增大
例2 用描点法画出正比例函数
(1)
y
=-2x;
的图象.
思考2 当k<0时,
(1)它的图象形状?
(2)位置怎样?
(3)图象的变化规律?
是一条直线
经过二、四象限
y随x的增大而减少
(0,0)点;
(4)
∣k∣值越大图像越靠近y轴
