4.1认识三角形 三角形的三边关系(共19张ppt)
文档属性
| 名称 | 4.1认识三角形 三角形的三边关系(共19张ppt) |

|
|
| 格式 | ppt | ||
| 文件大小 | 736.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-04-19 00:00:00 | ||
图片预览


文档简介
【4.1.2 】
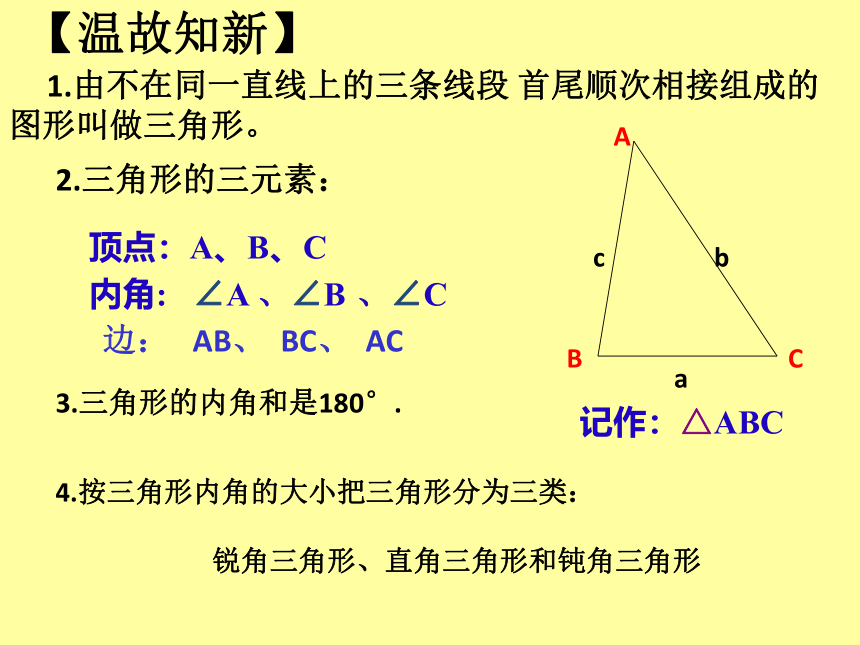
1.由不在同一直线上的三条线段 首尾顺次相接组成的图形叫做三角形。
2.三角形的三元素:
顶点:A、B、C
内角: ∠A 、∠B 、∠C
记作:△ABC
A
B
C
b
c
a
边: AB、 BC、 AC
3.三角形的内角和是180°.
【温故知新】
4.按三角形内角的大小把三角形分为三类:
锐角三角形、直角三角形和钝角三角形
① ② ③ ④
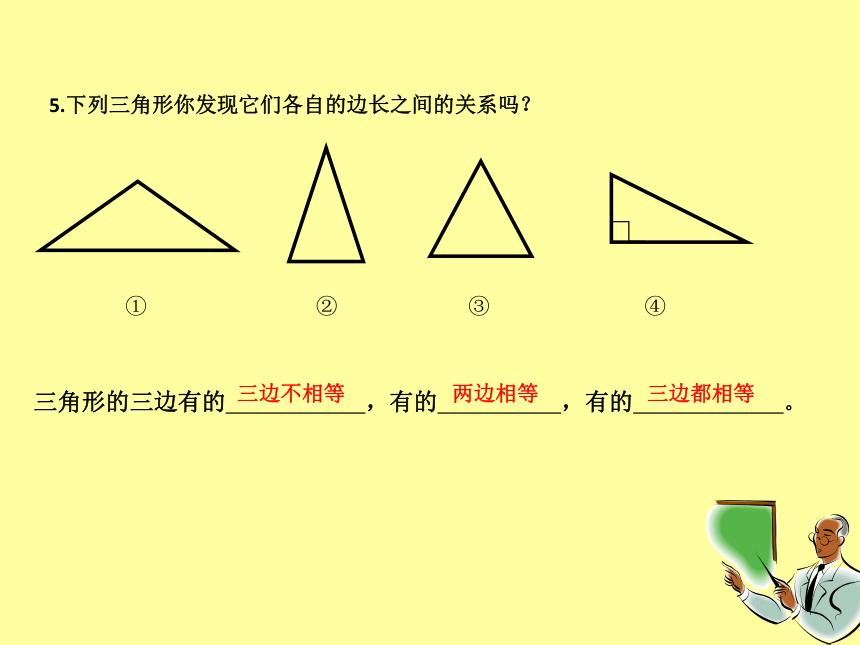
5.下列三角形你发现它们各自的边长之间的关系吗?
三角形的三边有的 ,有的 ,有的 。
三边不相等
两边相等
三边都相等
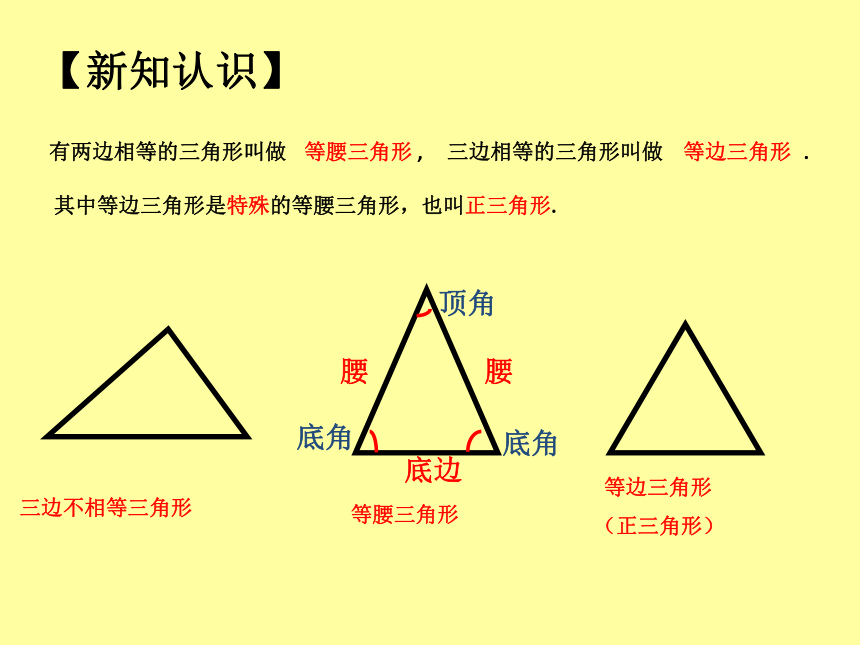
其中等边三角形是特殊的等腰三角形,也叫正三角形.
三边不相等三角形
等腰三角形
等边三角形
(正三角形)
腰
腰
底角
底角
底边
顶角
【新知认识】
有两边相等的三角形叫做 , 三边相等的三角形叫做 .
等腰三角形
等边三角形
【动手摆一摆】
老师给同学们准备了一些小棒,任取三根首位顺次相接拼摆三角形。同学们猜想一下,我们用任意三根一定能搭成三角形吗? (展台展示)
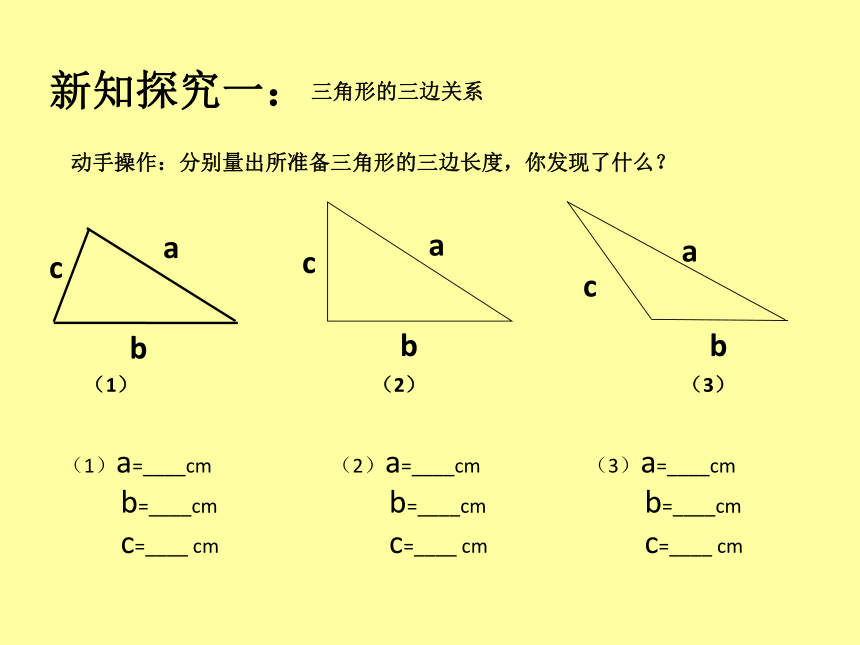
新知探究一:
三角形的三边关系
动手操作:分别量出所准备三角形的三边长度,你发现了什么?
a
a
a
b
b
b
c
c
c
(1)
(2)
(3)
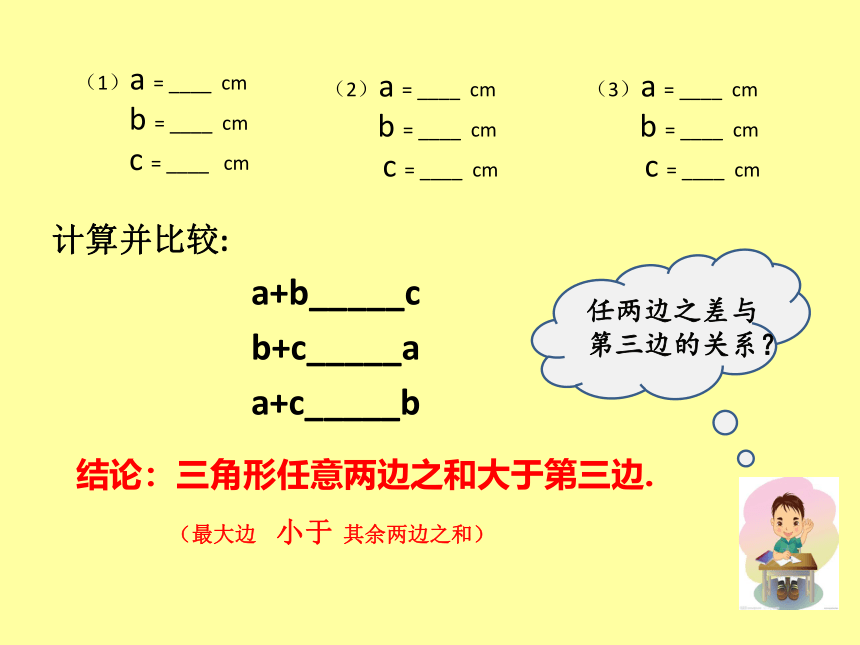
(1)a=____cm
b=____cm
c=____ cm
(2)a=____cm
b=____cm
c=____ cm
(3)a=____cm
b=____cm
c=____ cm
计算并比较:
a+b_____c
b+c_____a
a+c_____b
结论:三角形任意两边之和大于第三边.
(最大边 小于 其余两边之和)
(1)a = ____ cm
b = ____ cm
c = ____ cm
(2)a = ____ cm
b = ____ cm
c = ____ cm
(3)a = ____ cm
b = ____ cm
c = ____ cm
任两边之差与第三边的关系?
新知探究二:
三角形任意两边之差与第三边的关系
结论:三角形任意两边之差小于第三边.
( 最大边 — 最小边 < 第三边 )
利用刚刚测量的数据,任取三角形两边之差与第三边进行比较,你又发现了什么?
(1)a = ____ cm
b = ____ cm
c = ____ cm
(2)a = ____ cm
b = ____ cm
c = ____ cm
(3)a = ____ cm
b = ____ cm
c = ____ cm
(1)下列每组数分别是三根小木棒的长度,用它们能摆成三角形吗?
A.3cm, 4cm, 5cm ; B.8cm, 7cm, 15cm
C.13cm, 12cm, 20cm; D.5cm, 5cm, 11cm
(A,C)
解题技巧:
比较较小两边的和与最长边的大小即可
(2)下列四根木棒中,能与4cm、9cm长的两根木棒订成一个三角形的是
A. 6cm B. 5cm C. 9cm D. 13cm
(A,C)
有两根长度分别为5cm和8cm的木棒,用长度为2cm的木棒与它们能摆成三角形吗?为什么?长度为13cm的木棒呢?
解:取长度为2cm的木棒时,由于2+5=7 < 8,出现了两边之和小于第三边的情况,所以它们不能摆成三角形。
你能取一根木棒,与原来的两根木棒摆成三角形吗?
三角形第三边的取值范围:
两边之差 < 第三边 < 两边之和
取长度为13cm的木棒时,由于5+8=13,出现了两边之和等于第三边的情况,所以它们也不能摆成三角形。
3.已知三角形的两边长为4cm和7cm,
则此三角形第三边长是:( )
A.2cm B.3cm C.5cm D.11cm
c
8cm
4.等腰三角形一边长为8cm,另一边长为4cm,
第三边是 .
【我学会了··· ···】
1.三角形的三边关系:
三角形任意两边之和大于第三边。
三角形任意两边之差小于第三边。
2.判断三条线段能否组成三角形时,较为简便的判法:
如果较短的两条边的和大于第三条边,就可以构成三角形,否则就不能。
3.确定第三边的取值范围:
两边之差 < 第三边 < 两边之和
【课堂检测】
1.任意三条线段都能组成三角形。( )
2.如果a+b>c ,那么a ,b ,c 三条线段可以构成三角形。( )
3.若五条线段的长分别1cm, 2cm, 3cm, 4cm, 5cm, 则以其中三条线段为边可构成______个三角形。
4. 若等腰三角形的两边长分别是3和4,则它的周长为 。
若等腰三角形的两边长分别为3和7,则它的周长为_______ ;
5.已知两根木条长度分别为3cm和5cm ,要想拼成一个三角形,问第三根木条的长度a应取的范围______________ 。
6.一个三角形的两边长分别为2cm和9cm,若第三边长为奇数,则第三边长为 。
7.以下列各组线段为边,能组成三角形的是( )。
A. 1cm, 2cm, 4cm B. 8cm, 6cm, 4cm
C. 12cm, 5cm, 6cm D. 2cm, 3cm, 6cm
议一议
在A点有两只小狗,同时发现B点有一香肠,于是它们沿着各自不同的路线出发(假设它们的速度相同)你认为它们各自的路线是什么?谁先抢到香肠?为什么?
C
B
A
2.两点之间的所有连线中,线段最短
1.三角形任意两边之和大于第三边
人行横道
.A
.B
为什么经常有行人斜穿马路而不走人行横道
若△ABC的三边为a,b,c,则化简 a+b-c – b-a-c 的结果是( ).
(A) 2a-2b (B) 2a+2b+2c
(C) 2b-2c (D) 2a-2c
c
动动脑
某地有四个汽车停车场,位于如图所示的四边形ABCD的四个顶点,现在要建立一个汽车维修站,你能利用“三角形任意两边之和大于第三边”在四边形ABCD的内部找一点P,使点P到A,B,C,D四点的距离之和最小吗?
A
B
C
D
P
P1
作业布置:
习题4.2——1、2、3
1.由不在同一直线上的三条线段 首尾顺次相接组成的图形叫做三角形。
2.三角形的三元素:
顶点:A、B、C
内角: ∠A 、∠B 、∠C
记作:△ABC
A
B
C
b
c
a
边: AB、 BC、 AC
3.三角形的内角和是180°.
【温故知新】
4.按三角形内角的大小把三角形分为三类:
锐角三角形、直角三角形和钝角三角形
① ② ③ ④
5.下列三角形你发现它们各自的边长之间的关系吗?
三角形的三边有的 ,有的 ,有的 。
三边不相等
两边相等
三边都相等
其中等边三角形是特殊的等腰三角形,也叫正三角形.
三边不相等三角形
等腰三角形
等边三角形
(正三角形)
腰
腰
底角
底角
底边
顶角
【新知认识】
有两边相等的三角形叫做 , 三边相等的三角形叫做 .
等腰三角形
等边三角形
【动手摆一摆】
老师给同学们准备了一些小棒,任取三根首位顺次相接拼摆三角形。同学们猜想一下,我们用任意三根一定能搭成三角形吗? (展台展示)
新知探究一:
三角形的三边关系
动手操作:分别量出所准备三角形的三边长度,你发现了什么?
a
a
a
b
b
b
c
c
c
(1)
(2)
(3)
(1)a=____cm
b=____cm
c=____ cm
(2)a=____cm
b=____cm
c=____ cm
(3)a=____cm
b=____cm
c=____ cm
计算并比较:
a+b_____c
b+c_____a
a+c_____b
结论:三角形任意两边之和大于第三边.
(最大边 小于 其余两边之和)
(1)a = ____ cm
b = ____ cm
c = ____ cm
(2)a = ____ cm
b = ____ cm
c = ____ cm
(3)a = ____ cm
b = ____ cm
c = ____ cm
任两边之差与第三边的关系?
新知探究二:
三角形任意两边之差与第三边的关系
结论:三角形任意两边之差小于第三边.
( 最大边 — 最小边 < 第三边 )
利用刚刚测量的数据,任取三角形两边之差与第三边进行比较,你又发现了什么?
(1)a = ____ cm
b = ____ cm
c = ____ cm
(2)a = ____ cm
b = ____ cm
c = ____ cm
(3)a = ____ cm
b = ____ cm
c = ____ cm
(1)下列每组数分别是三根小木棒的长度,用它们能摆成三角形吗?
A.3cm, 4cm, 5cm ; B.8cm, 7cm, 15cm
C.13cm, 12cm, 20cm; D.5cm, 5cm, 11cm
(A,C)
解题技巧:
比较较小两边的和与最长边的大小即可
(2)下列四根木棒中,能与4cm、9cm长的两根木棒订成一个三角形的是
A. 6cm B. 5cm C. 9cm D. 13cm
(A,C)
有两根长度分别为5cm和8cm的木棒,用长度为2cm的木棒与它们能摆成三角形吗?为什么?长度为13cm的木棒呢?
解:取长度为2cm的木棒时,由于2+5=7 < 8,出现了两边之和小于第三边的情况,所以它们不能摆成三角形。
你能取一根木棒,与原来的两根木棒摆成三角形吗?
三角形第三边的取值范围:
两边之差 < 第三边 < 两边之和
取长度为13cm的木棒时,由于5+8=13,出现了两边之和等于第三边的情况,所以它们也不能摆成三角形。
3.已知三角形的两边长为4cm和7cm,
则此三角形第三边长是:( )
A.2cm B.3cm C.5cm D.11cm
c
8cm
4.等腰三角形一边长为8cm,另一边长为4cm,
第三边是 .
【我学会了··· ···】
1.三角形的三边关系:
三角形任意两边之和大于第三边。
三角形任意两边之差小于第三边。
2.判断三条线段能否组成三角形时,较为简便的判法:
如果较短的两条边的和大于第三条边,就可以构成三角形,否则就不能。
3.确定第三边的取值范围:
两边之差 < 第三边 < 两边之和
【课堂检测】
1.任意三条线段都能组成三角形。( )
2.如果a+b>c ,那么a ,b ,c 三条线段可以构成三角形。( )
3.若五条线段的长分别1cm, 2cm, 3cm, 4cm, 5cm, 则以其中三条线段为边可构成______个三角形。
4. 若等腰三角形的两边长分别是3和4,则它的周长为 。
若等腰三角形的两边长分别为3和7,则它的周长为_______ ;
5.已知两根木条长度分别为3cm和5cm ,要想拼成一个三角形,问第三根木条的长度a应取的范围______________ 。
6.一个三角形的两边长分别为2cm和9cm,若第三边长为奇数,则第三边长为 。
7.以下列各组线段为边,能组成三角形的是( )。
A. 1cm, 2cm, 4cm B. 8cm, 6cm, 4cm
C. 12cm, 5cm, 6cm D. 2cm, 3cm, 6cm
议一议
在A点有两只小狗,同时发现B点有一香肠,于是它们沿着各自不同的路线出发(假设它们的速度相同)你认为它们各自的路线是什么?谁先抢到香肠?为什么?
C
B
A
2.两点之间的所有连线中,线段最短
1.三角形任意两边之和大于第三边
人行横道
.A
.B
为什么经常有行人斜穿马路而不走人行横道
若△ABC的三边为a,b,c,则化简 a+b-c – b-a-c 的结果是( ).
(A) 2a-2b (B) 2a+2b+2c
(C) 2b-2c (D) 2a-2c
c
动动脑
某地有四个汽车停车场,位于如图所示的四边形ABCD的四个顶点,现在要建立一个汽车维修站,你能利用“三角形任意两边之和大于第三边”在四边形ABCD的内部找一点P,使点P到A,B,C,D四点的距离之和最小吗?
A
B
C
D
P
P1
作业布置:
习题4.2——1、2、3
同课章节目录
- 第一章 整式的乘除
- 1 同底数幂的乘法
- 2 幂的乘方与积的乘方
- 3 同底数幂的除法
- 4 整式的乘法
- 5 平方差公式
- 6 完全平方公式
- 7 整式的除法
- 第二章 相交线与平行线
- 1 两条直线的位置关系
- 2 探索直线平行的条件
- 3 平行线的性质
- 4 用尺规作角
- 第三章 变量之间的关系
- 1 用表格表示的变量间关系
- 2 用关系式表示的变量间关系
- 3 用图象表示的变量间关系
- 第四章 三角形
- 1 认识三角形
- 2 图形的全等
- 3 探索三角形全等的条件
- 4 用尺规作三角形
- 5 利用三角形全等测距离
- 第五章 生活中的轴对称
- 1 轴对称现象
- 2 探索轴对称的性质
- 3 简单的轴对称图形
- 4 利用轴对称进行设计
- 第六章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
