4.3探索三角形全等的条件 角边角、角角边判定(共21张ppt)
文档属性
| 名称 | 4.3探索三角形全等的条件 角边角、角角边判定(共21张ppt) |

|
|
| 格式 | ppt | ||
| 文件大小 | 429.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-04-19 00:00:00 | ||
图片预览


文档简介
九年级数学中考总复习
考点一:全等图形及全等三角形
1.能够完全________的两个图形称为全等图形,
全等图形的形状和大小都相同.
2.能够完全______的两个三角形叫全等三角形.
温馨提示:完全重合有两层含义:
(1)图形的形状相同;(2)图形的大小相等.
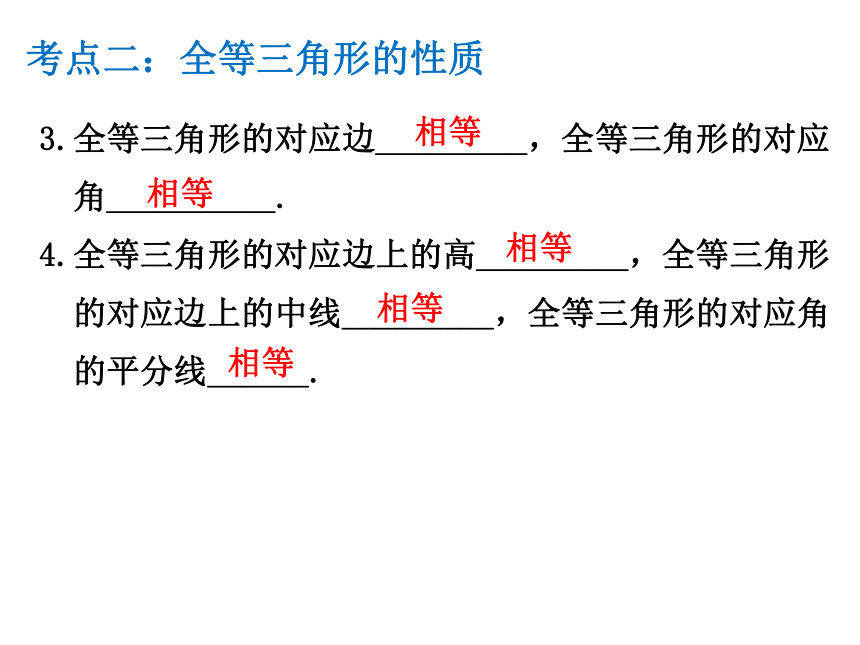
考点二:全等三角形的性质
3.全等三角形的对应边_________,全等三角形的对应
角__________.
4.全等三角形的对应边上的高_________,全等三角形
的对应边上的中线_________,全等三角形的对应角
的平分线______.
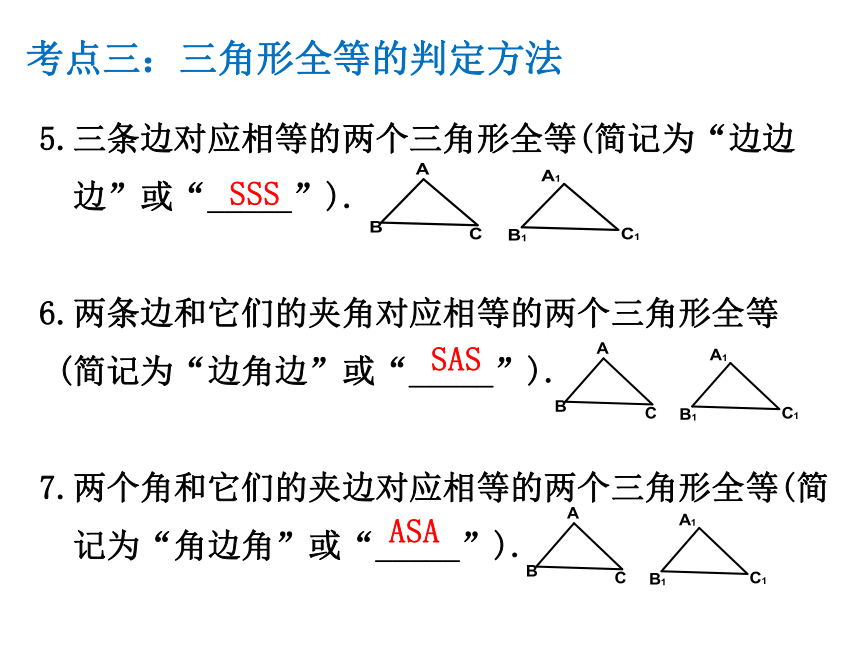
考点三:三角形全等的判定方法
5.三条边对应相等的两个三角形全等(简记为“边边
边”或“_____”).
6.两条边和它们的夹角对应相等的两个三角形全等
(简记为“边角边”或“_____”).
7.两个角和它们的夹边对应相等的两个三角形全等(简
记为“角边角”或“_____”).
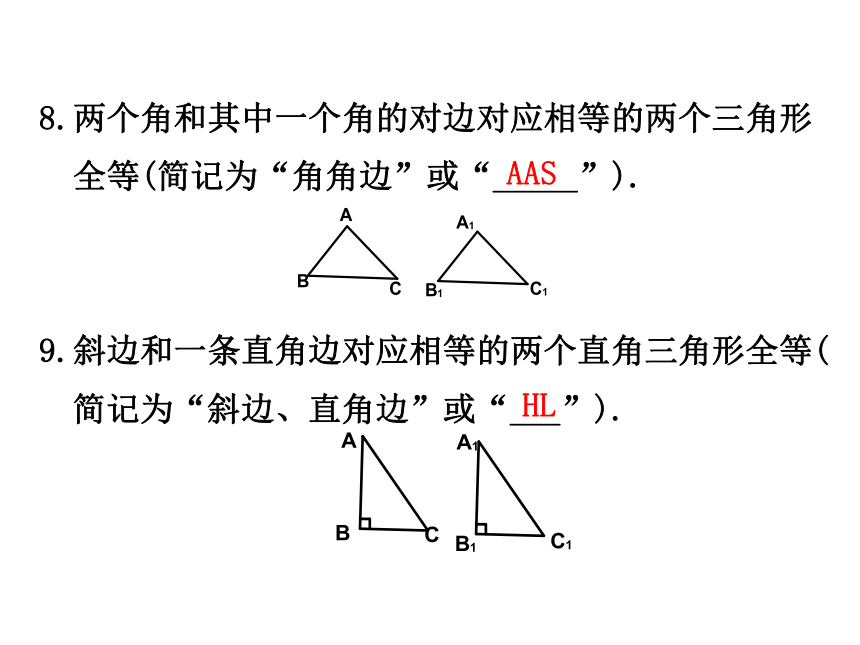
8.两个角和其中一个角的对边对应相等的两个三角形
全等(简记为“角角边”或“_____”).
9.斜边和一条直角边对应相等的两个直角三角形全等(
简记为“斜边、直角边”或“___”).
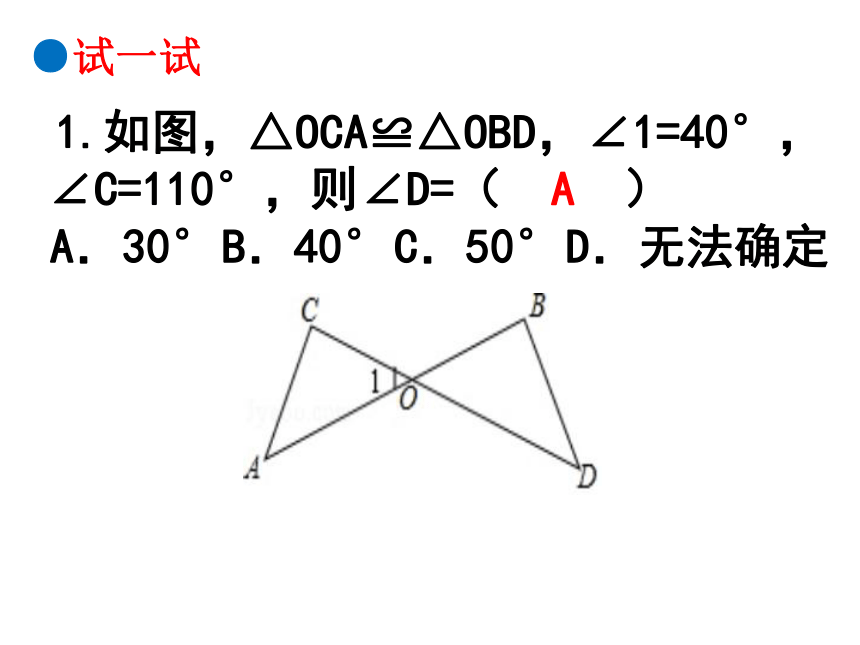
1.如图,△OCA≌△OBD,∠1=40°,
∠C=110°,则∠D=( A )
A.30° B.40° C.50° D.无法确定
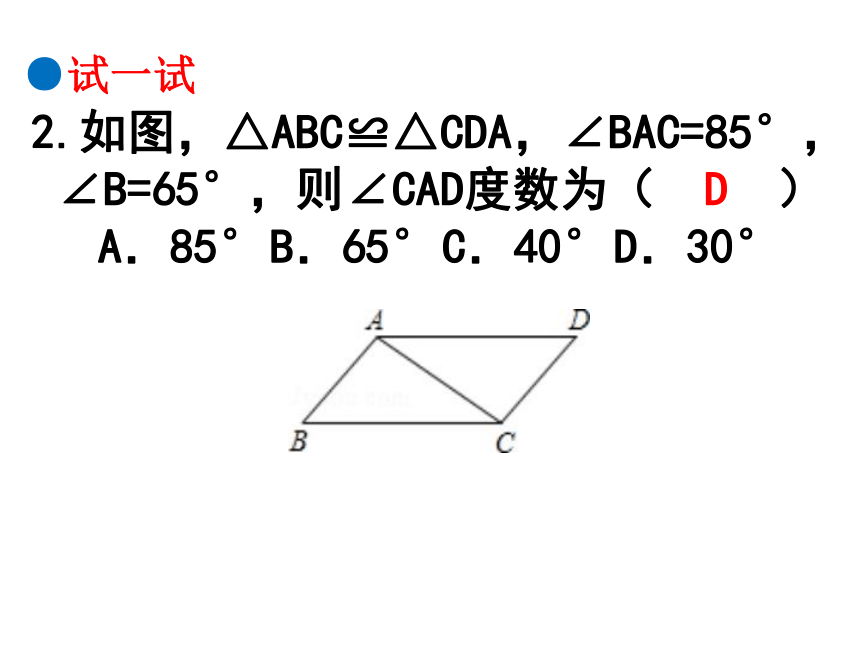
2.如图,△ABC≌△CDA,∠BAC=85°,∠B=65°,则∠CAD度数为( D )
A.85° B.65° C.40° D.30°
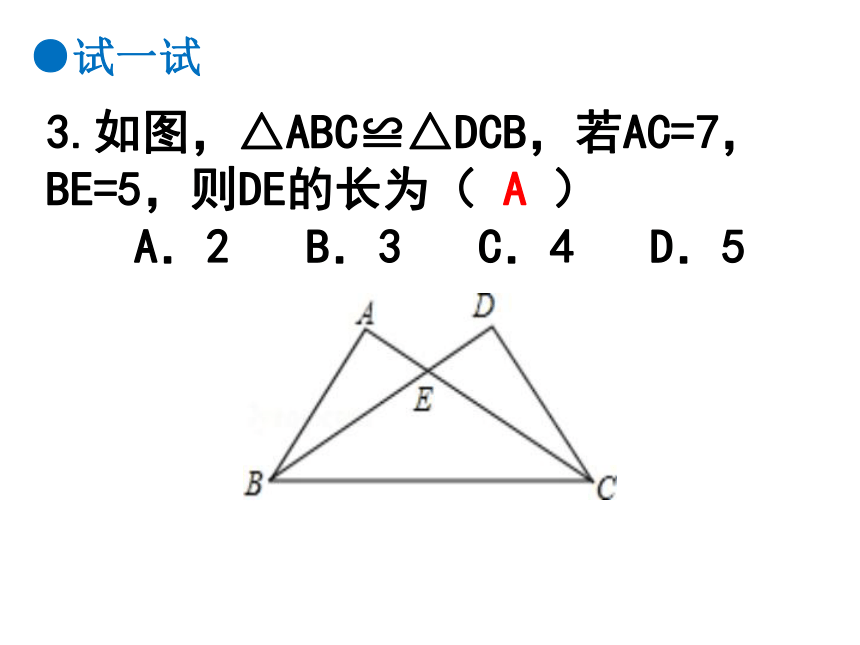
3.如图,△ABC≌△DCB,若AC=7,BE=5,则DE的长为( A )
A.2 B.3 C.4 D.5
?
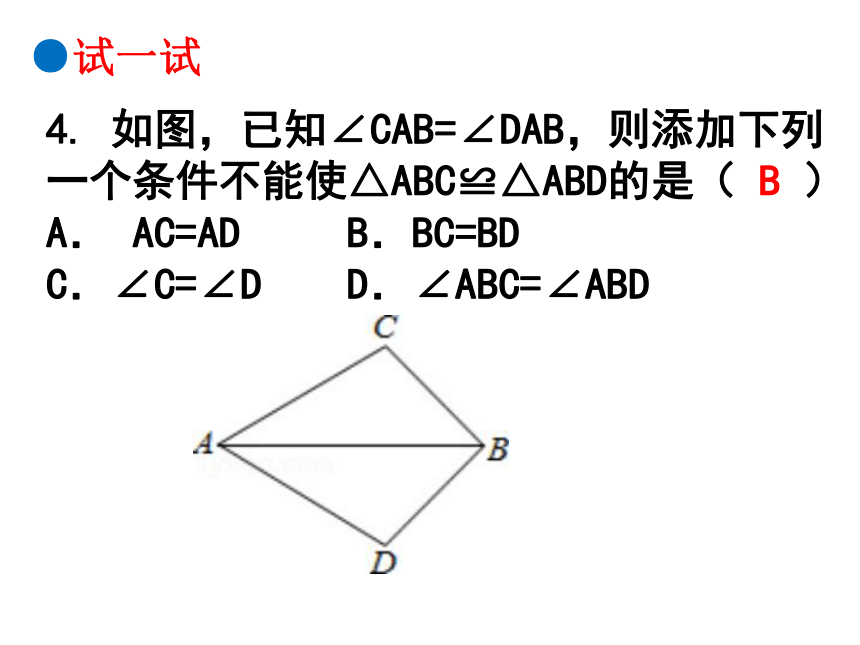
4. 如图,已知∠CAB=∠DAB,则添加下列一个条件不能使△ABC≌△ABD的是( B ) A. AC=AD B.BC=BD
C.∠C=∠D D.∠ABC=∠ABD
5.如图,∠B=∠D=90°,BC=CD,∠1=40°,则∠2=( B )
A.40° B.50° C.60° D.75°
?
1.(2017.怀化市)如图,点C,F,E,B在一条直线上,∠CFD=∠BEA,CE=BF,DF=AE.写
出CD与AB之间的关系,并证明你的结论。
1.(2017?广州)如图,点E,F在AB上,AD=BC,∠A=∠B,AE=BF.求证:△ADF≌△BCE.
?
?
?
1、如图,已知AB=DE,∠B=∠E, 请你添加一个条件使△ABF≌△DEC,需要添加的条件是_______.理由是:_________.
A
D
B C F E
∠A=∠D
ASA
或BF=EC
SAS
BC=EF
或∠AFB=∠DCE
AAS
2.(2016·南京市)如图,四边形ABCD的对角线
AC,BD相交于点O,△ABO≌△ADO.下列结论:
①AC⊥BD;②CB=CD;③△ABC≌△ADC;④DA=DC.
其中正确结论的序号是____________.
①②③
1.(2015.广东)如题21图,在边长为6的正方形ABCD中,E是边CD的中点,将△ADE沿AE对折至△AFE,延长EF交BC于点G,连接AG.(1)求证:△ABG≌△AFG;(2) 求BG的长.
?
?
?
?
(1)证明:∵四边形ABCD是正方形,
∴∠B=∠D=90°,AD=AB.
由折叠的性质,得AD=AF,∠AFE=∠D=90°.
∴∠AFG=90°,AB=AF.
又∵AG=AG,∴Rt△ABG≌Rt△AFG(HL).
(2)解:∵△ABG≌△AFG,∴BG=FG.
设BG=FG=x, 则GC=6-x.
∵E为CD的中点,∴CE=EF=DE=3.∴EG=x+3.
∴在Rt△CGE中,32+(6-x)2=(x+3)2,
解得x=2. ∴BG=2.
2. 已知:如图△ABC是等边三角形,过AB边上的点D作DG∥BC,交AC于点G,在GD的延长线上
取点E,使DE=DB,连接AE、CD.
(1)求证:△AGE≌△DAC;
(2)过点E作EF∥DC,交BC于点F,请你连接AF,并判断△AEF是怎样的三角形,试证明你的结论.
?
?
?
?
(1)证明:∵△ABC是等边三角形,
∴AB=AC=BC,∠BAC=∠ABC=∠ACB=60°.
∵EG∥BC ∴∠ADG=∠ABC=60°∠AGD=∠ACB=60°.
∴△ADG是等边三角形.
∴AD=DG=AG.
∵DE=DB, ∴EG=AB ∴GE=AC.
∵EG=AB=CA,∴∠AGE=∠DAC=60°,
在△AGE和△DAC中,
∴△AGE≌△DAC (SAS)
(2)解:△AEF为等边三角形.
证明:如图,连接AF,
∵DG∥BC,EF∥DC,
∴四边形EFCD是平行四边形,
∴EF=CD,∠DEF=∠DCF,
由(1)知△AGE≌△DAC,
∴AE=CD,∠AED=∠ACD.
∵EF=CD=AE,
∠AED+∠DEF=∠ACD+∠DCB=60°,
∴△AEF为等边三角形.
本节课你有什么收获?
以后还学其他
反思回顾
书山有路勤为径,
学海无涯苦作舟。
祝愿大家在今后的生活
学习中天天开心、快乐!
考点一:全等图形及全等三角形
1.能够完全________的两个图形称为全等图形,
全等图形的形状和大小都相同.
2.能够完全______的两个三角形叫全等三角形.
温馨提示:完全重合有两层含义:
(1)图形的形状相同;(2)图形的大小相等.
考点二:全等三角形的性质
3.全等三角形的对应边_________,全等三角形的对应
角__________.
4.全等三角形的对应边上的高_________,全等三角形
的对应边上的中线_________,全等三角形的对应角
的平分线______.
考点三:三角形全等的判定方法
5.三条边对应相等的两个三角形全等(简记为“边边
边”或“_____”).
6.两条边和它们的夹角对应相等的两个三角形全等
(简记为“边角边”或“_____”).
7.两个角和它们的夹边对应相等的两个三角形全等(简
记为“角边角”或“_____”).
8.两个角和其中一个角的对边对应相等的两个三角形
全等(简记为“角角边”或“_____”).
9.斜边和一条直角边对应相等的两个直角三角形全等(
简记为“斜边、直角边”或“___”).
1.如图,△OCA≌△OBD,∠1=40°,
∠C=110°,则∠D=( A )
A.30° B.40° C.50° D.无法确定
2.如图,△ABC≌△CDA,∠BAC=85°,∠B=65°,则∠CAD度数为( D )
A.85° B.65° C.40° D.30°
3.如图,△ABC≌△DCB,若AC=7,BE=5,则DE的长为( A )
A.2 B.3 C.4 D.5
?
4. 如图,已知∠CAB=∠DAB,则添加下列一个条件不能使△ABC≌△ABD的是( B ) A. AC=AD B.BC=BD
C.∠C=∠D D.∠ABC=∠ABD
5.如图,∠B=∠D=90°,BC=CD,∠1=40°,则∠2=( B )
A.40° B.50° C.60° D.75°
?
1.(2017.怀化市)如图,点C,F,E,B在一条直线上,∠CFD=∠BEA,CE=BF,DF=AE.写
出CD与AB之间的关系,并证明你的结论。
1.(2017?广州)如图,点E,F在AB上,AD=BC,∠A=∠B,AE=BF.求证:△ADF≌△BCE.
?
?
?
1、如图,已知AB=DE,∠B=∠E, 请你添加一个条件使△ABF≌△DEC,需要添加的条件是_______.理由是:_________.
A
D
B C F E
∠A=∠D
ASA
或BF=EC
SAS
BC=EF
或∠AFB=∠DCE
AAS
2.(2016·南京市)如图,四边形ABCD的对角线
AC,BD相交于点O,△ABO≌△ADO.下列结论:
①AC⊥BD;②CB=CD;③△ABC≌△ADC;④DA=DC.
其中正确结论的序号是____________.
①②③
1.(2015.广东)如题21图,在边长为6的正方形ABCD中,E是边CD的中点,将△ADE沿AE对折至△AFE,延长EF交BC于点G,连接AG.(1)求证:△ABG≌△AFG;(2) 求BG的长.
?
?
?
?
(1)证明:∵四边形ABCD是正方形,
∴∠B=∠D=90°,AD=AB.
由折叠的性质,得AD=AF,∠AFE=∠D=90°.
∴∠AFG=90°,AB=AF.
又∵AG=AG,∴Rt△ABG≌Rt△AFG(HL).
(2)解:∵△ABG≌△AFG,∴BG=FG.
设BG=FG=x, 则GC=6-x.
∵E为CD的中点,∴CE=EF=DE=3.∴EG=x+3.
∴在Rt△CGE中,32+(6-x)2=(x+3)2,
解得x=2. ∴BG=2.
2. 已知:如图△ABC是等边三角形,过AB边上的点D作DG∥BC,交AC于点G,在GD的延长线上
取点E,使DE=DB,连接AE、CD.
(1)求证:△AGE≌△DAC;
(2)过点E作EF∥DC,交BC于点F,请你连接AF,并判断△AEF是怎样的三角形,试证明你的结论.
?
?
?
?
(1)证明:∵△ABC是等边三角形,
∴AB=AC=BC,∠BAC=∠ABC=∠ACB=60°.
∵EG∥BC ∴∠ADG=∠ABC=60°∠AGD=∠ACB=60°.
∴△ADG是等边三角形.
∴AD=DG=AG.
∵DE=DB, ∴EG=AB ∴GE=AC.
∵EG=AB=CA,∴∠AGE=∠DAC=60°,
在△AGE和△DAC中,
∴△AGE≌△DAC (SAS)
(2)解:△AEF为等边三角形.
证明:如图,连接AF,
∵DG∥BC,EF∥DC,
∴四边形EFCD是平行四边形,
∴EF=CD,∠DEF=∠DCF,
由(1)知△AGE≌△DAC,
∴AE=CD,∠AED=∠ACD.
∵EF=CD=AE,
∠AED+∠DEF=∠ACD+∠DCB=60°,
∴△AEF为等边三角形.
本节课你有什么收获?
以后还学其他
反思回顾
书山有路勤为径,
学海无涯苦作舟。
祝愿大家在今后的生活
学习中天天开心、快乐!
同课章节目录
- 第一章 整式的乘除
- 1 同底数幂的乘法
- 2 幂的乘方与积的乘方
- 3 同底数幂的除法
- 4 整式的乘法
- 5 平方差公式
- 6 完全平方公式
- 7 整式的除法
- 第二章 相交线与平行线
- 1 两条直线的位置关系
- 2 探索直线平行的条件
- 3 平行线的性质
- 4 用尺规作角
- 第三章 变量之间的关系
- 1 用表格表示的变量间关系
- 2 用关系式表示的变量间关系
- 3 用图象表示的变量间关系
- 第四章 三角形
- 1 认识三角形
- 2 图形的全等
- 3 探索三角形全等的条件
- 4 用尺规作三角形
- 5 利用三角形全等测距离
- 第五章 生活中的轴对称
- 1 轴对称现象
- 2 探索轴对称的性质
- 3 简单的轴对称图形
- 4 利用轴对称进行设计
- 第六章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
