2020—2021学年八年级数学人教版下册16.3.2二次根式的混合运算课件(共39张ppt)
文档属性
| 名称 | 2020—2021学年八年级数学人教版下册16.3.2二次根式的混合运算课件(共39张ppt) |  | |
| 格式 | zip | ||
| 文件大小 | 1.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-04-19 10:46:18 | ||
图片预览







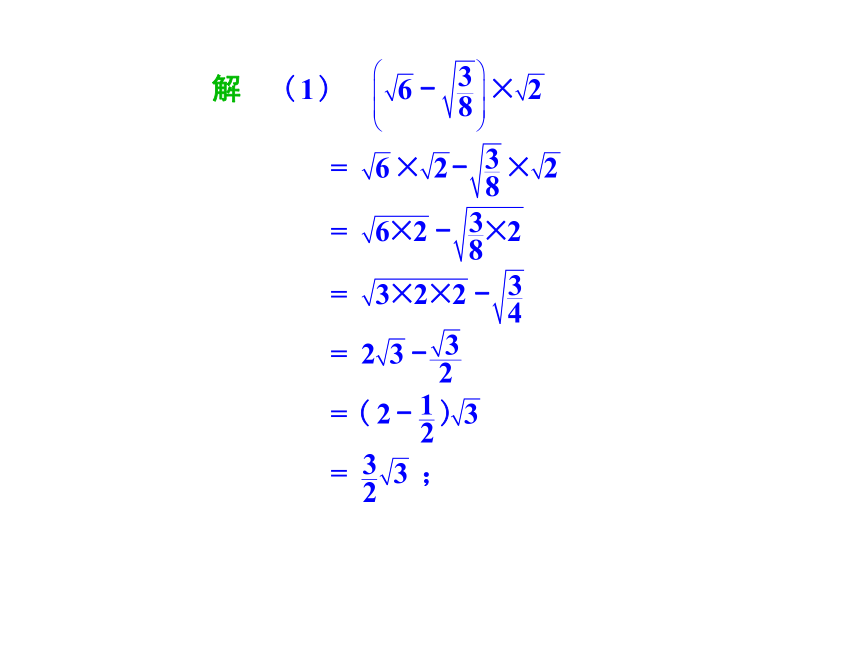
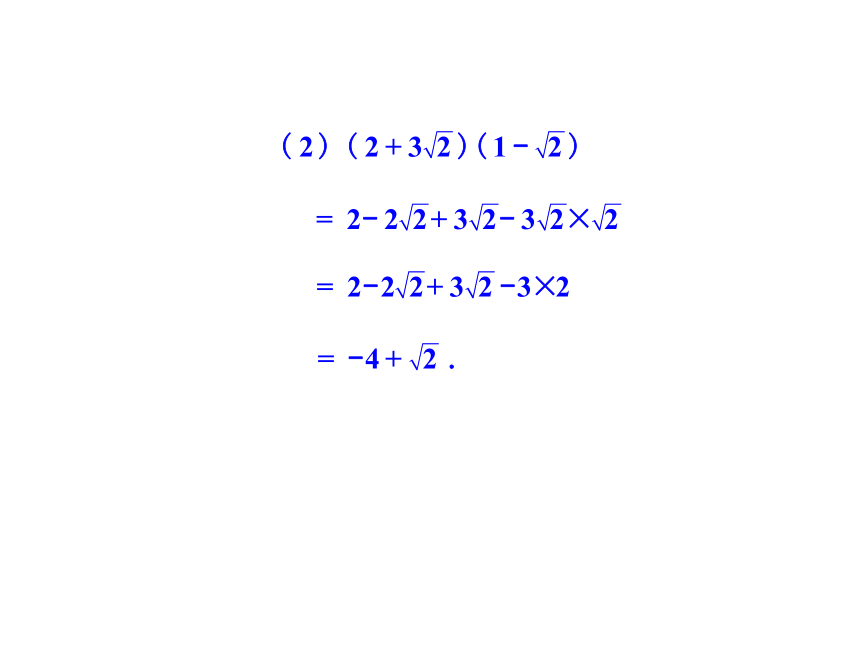



文档简介
(共39张PPT)
二次根式的混合运算
二次根式的混合运算
1、二次根式的混合运算是指二次根式的____、____、____、____的混合运算.
2、二次根式的混合运算顺序与实数的运算顺序相同:
先算_______,后算_______,有括号的先算括号里面的.
加
减
乘
除
乘除
加减
二次根式的混合运算:
3、二次根式的加减运算步骤:①
②
4、二次根式的乘法运算公式:
5、二次根式的除法运算公式:
2.整式乘法中多项式与多项式相乘的法则用字母
表示为
1.整式乘法中单项式乘以多项式的法则用字母
表示为:
一、借用整式乘法的法则进行二次根式混合运算。
.
乘法公式中平方差公式、完全平方公式用字母如何表示?
1、平方差公式:
。
2、完全平方和公式:
。
3、完全平方差公式:
。
二、套用乘法公式进行二次根式混合运算
说一说
如果梯形的上、下底长分别为
高为
,那么它的面积是多少?
举
例
例3
计算:
二次根式的混合运算是根据实数的运算律进行的.
从例3的第(2)小题看到,二次根式的和相乘,与多项式的乘法相类似.
例3
计算:
我们可以利用多项式的乘法公式,进行某些二次根式的和相乘的运算.
举
例
例4
计算:
从例4的第(1)小题的结果受到启发,把分子与分母都乘以
,就可以使分母变成1.
动脑筋
如何计算
?
举
例
例5
计算:
1.
计算:
练习
1、计算:
注意:
1、运算顺序
。
2、运用运算律和乘法公式,简化运算。
3、结果为最简二次根式。
1、分母有理化的定义:
把分母中的根号化去。
2、方法:
分子、分母同时乘以分母的有理化因式。
3、有理化因式:
4、常见的互为有理化因式:
两个含有二次根式的代数式相乘,如果它们的积中不含二次根式
,我们说这两个二次根式互为有理化因式。
的有理化因式:
二、巧用“分母有理化”进行二次根式混合运算
二次根式运算
(提高篇)
一:二次根式混合运算
例1:计算:(每小题4分)
〉〉解题示范——规范步骤,该得的分一分不丢!
[2分]
[4分]
[4分]
(3)已知
的整数部分为a,小数部分为b,求a2-b2的值.
知能迁移:
二:二次根式运算中的技巧
例2:
1.x2+xy+y2是一个对称式,可先求出基本对称式x+y=4,
xy=1,然后将x2+xy+y2转化为(x+y)2-xy,整体代入即
可.
(3)已知a=3+2
,b=3-2
,求a2b-ab2的值;
解:∵a-b=(3+2
)-(3-2
)=4
,
ab=(3+2
)(3-2
)=-11,
∴a2b-ab2=ab(a-b)=(-11)×4
=-44
.
(4)已知x=
,y=
,求
的值;
解:∵x=
=(
-1)2=3-2
,
y=
=(
+1)2=3+2
,
∴x+y=6,x-y=-4
,xy=1.
原式=
=
=
=-
.
2
-
1
2
+
1
2
+
1
-
1
2
2
-
1
2
+
1
2
-
1
2
+
1
三:注意二次根式运算中隐含条件
例3
已知:a=
,求
-
的值.
学生作答 解:原式=
-
=a-1-
=a-1-
.
∴当a=
时,
原式=
-1-(2+
)=-1-2
.
规范解答
解:∵a=
<1,∴a-1<0.
∴
=
=|a-1|=1-a.
∴原式=
-
=a-1+
.
∴当a=
时,
原式=
-1+(2+
)=3.
计算
(1)
a(a+b)
(2)
(3)
解:(1)原式=
(2)原式=
(3)
原式=
(4).
(4)原式=
(5)原式=
(5)
:相信自己能行
=2
例题讲析
例1.计算
(2)
解:原式=
解:原式=
(1)
(我是小老师)
例2.
计算
(1)
(2)
解:原式=
解:原式=
例3.先化简,再求值
,其中
解:原式=
当
时,
原式=
课堂展示
1.计算
(2)
(3)
(4)
(1)
第一轮
解:原式=
解:原式=
解:原式=
解:原式=
第二轮
(2)
(3)
(4)
2.计算
(1)
解:原式=
解:原式=
解:原式=
解:原式=
课堂小结
在进行二次根式的运算时,类比整式的运算,灵活合理运用恰当的方法,
要注意过程和结果的正确
老师忠告
(1)题目中的隐含条件为a=
<1,所以
=
=|a-1|=1-a,而不是a-1;
(2)注意挖掘题目中的隐含条件,是解决数学问题的关键之一,上题中的隐含条件a=
=
=|a-1|
=1-a是进行二次根式化简的依据,同学们应注重分析能力
的培养,提高解题的正确性.
练习:
1.已知ab=3,求
的值
2.已知a+b=-8,ab=12,求
的值
2.
已知
2
求
3a
+
5b
–
c
的值。
先化简,再求值:
2
2
,
其中a
=
1:
解:
例5:化简:
解:原式=
2
2
=
=
=
=
-
2
1
已知a,b分别是
的整数部分和小数部分,
那么a
–
2b
的值是
;
2
已知
x
+
3x-1=0,
2
求
的值。
2
2
二次根式的混合运算
二次根式的混合运算
1、二次根式的混合运算是指二次根式的____、____、____、____的混合运算.
2、二次根式的混合运算顺序与实数的运算顺序相同:
先算_______,后算_______,有括号的先算括号里面的.
加
减
乘
除
乘除
加减
二次根式的混合运算:
3、二次根式的加减运算步骤:①
②
4、二次根式的乘法运算公式:
5、二次根式的除法运算公式:
2.整式乘法中多项式与多项式相乘的法则用字母
表示为
1.整式乘法中单项式乘以多项式的法则用字母
表示为:
一、借用整式乘法的法则进行二次根式混合运算。
.
乘法公式中平方差公式、完全平方公式用字母如何表示?
1、平方差公式:
。
2、完全平方和公式:
。
3、完全平方差公式:
。
二、套用乘法公式进行二次根式混合运算
说一说
如果梯形的上、下底长分别为
高为
,那么它的面积是多少?
举
例
例3
计算:
二次根式的混合运算是根据实数的运算律进行的.
从例3的第(2)小题看到,二次根式的和相乘,与多项式的乘法相类似.
例3
计算:
我们可以利用多项式的乘法公式,进行某些二次根式的和相乘的运算.
举
例
例4
计算:
从例4的第(1)小题的结果受到启发,把分子与分母都乘以
,就可以使分母变成1.
动脑筋
如何计算
?
举
例
例5
计算:
1.
计算:
练习
1、计算:
注意:
1、运算顺序
。
2、运用运算律和乘法公式,简化运算。
3、结果为最简二次根式。
1、分母有理化的定义:
把分母中的根号化去。
2、方法:
分子、分母同时乘以分母的有理化因式。
3、有理化因式:
4、常见的互为有理化因式:
两个含有二次根式的代数式相乘,如果它们的积中不含二次根式
,我们说这两个二次根式互为有理化因式。
的有理化因式:
二、巧用“分母有理化”进行二次根式混合运算
二次根式运算
(提高篇)
一:二次根式混合运算
例1:计算:(每小题4分)
〉〉解题示范——规范步骤,该得的分一分不丢!
[2分]
[4分]
[4分]
(3)已知
的整数部分为a,小数部分为b,求a2-b2的值.
知能迁移:
二:二次根式运算中的技巧
例2:
1.x2+xy+y2是一个对称式,可先求出基本对称式x+y=4,
xy=1,然后将x2+xy+y2转化为(x+y)2-xy,整体代入即
可.
(3)已知a=3+2
,b=3-2
,求a2b-ab2的值;
解:∵a-b=(3+2
)-(3-2
)=4
,
ab=(3+2
)(3-2
)=-11,
∴a2b-ab2=ab(a-b)=(-11)×4
=-44
.
(4)已知x=
,y=
,求
的值;
解:∵x=
=(
-1)2=3-2
,
y=
=(
+1)2=3+2
,
∴x+y=6,x-y=-4
,xy=1.
原式=
=
=
=-
.
2
-
1
2
+
1
2
+
1
-
1
2
2
-
1
2
+
1
2
-
1
2
+
1
三:注意二次根式运算中隐含条件
例3
已知:a=
,求
-
的值.
学生作答 解:原式=
-
=a-1-
=a-1-
.
∴当a=
时,
原式=
-1-(2+
)=-1-2
.
规范解答
解:∵a=
<1,∴a-1<0.
∴
=
=|a-1|=1-a.
∴原式=
-
=a-1+
.
∴当a=
时,
原式=
-1+(2+
)=3.
计算
(1)
a(a+b)
(2)
(3)
解:(1)原式=
(2)原式=
(3)
原式=
(4).
(4)原式=
(5)原式=
(5)
:相信自己能行
=2
例题讲析
例1.计算
(2)
解:原式=
解:原式=
(1)
(我是小老师)
例2.
计算
(1)
(2)
解:原式=
解:原式=
例3.先化简,再求值
,其中
解:原式=
当
时,
原式=
课堂展示
1.计算
(2)
(3)
(4)
(1)
第一轮
解:原式=
解:原式=
解:原式=
解:原式=
第二轮
(2)
(3)
(4)
2.计算
(1)
解:原式=
解:原式=
解:原式=
解:原式=
课堂小结
在进行二次根式的运算时,类比整式的运算,灵活合理运用恰当的方法,
要注意过程和结果的正确
老师忠告
(1)题目中的隐含条件为a=
<1,所以
=
=|a-1|=1-a,而不是a-1;
(2)注意挖掘题目中的隐含条件,是解决数学问题的关键之一,上题中的隐含条件a=
=
=|a-1|
=1-a是进行二次根式化简的依据,同学们应注重分析能力
的培养,提高解题的正确性.
练习:
1.已知ab=3,求
的值
2.已知a+b=-8,ab=12,求
的值
2.
已知
2
求
3a
+
5b
–
c
的值。
先化简,再求值:
2
2
,
其中a
=
1:
解:
例5:化简:
解:原式=
2
2
=
=
=
=
-
2
1
已知a,b分别是
的整数部分和小数部分,
那么a
–
2b
的值是
;
2
已知
x
+
3x-1=0,
2
求
的值。
2
2
