1.1计数原理-2020-2021学年人教A版高中数学选修2-3同步课时练(Word含答案)
文档属性
| 名称 | 1.1计数原理-2020-2021学年人教A版高中数学选修2-3同步课时练(Word含答案) |
|
|
| 格式 | doc | ||
| 文件大小 | 205.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-04-18 00:00:00 | ||
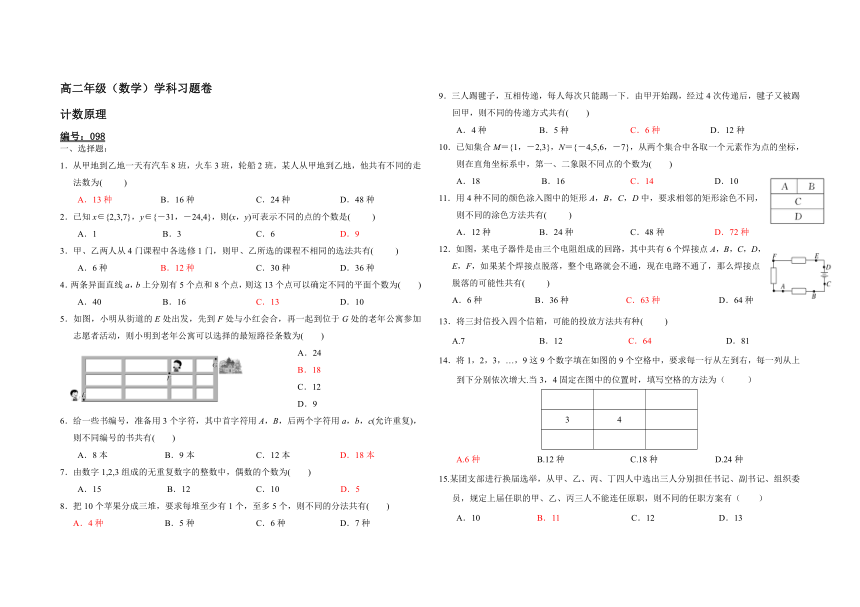
图片预览

文档简介
高二年级(数学)学科习题卷
计数原理
编号:098
一、选择题:
1.从甲地到乙地一天有汽车8班,火车3班,轮船2班,某人从甲地到乙地,他共有不同的走法数为( )
A.13种 B.16种 C.24种 D.48种
2.已知x∈{2,3,7},y∈{-31,-24,4},则(x,y)可表示不同的点的个数是( )
A.1 B.3 C.6 D.9
3.甲、乙两人从4门课程中各选修1门,则甲、乙所选的课程不相同的选法共有( )
A.6种 B.12种 C.30种 D.36种
4.两条异面直线a,b上分别有5个点和8个点,则这13个点可以确定不同的平面个数为( )
A.40 B.16 C.13 D.10
5.如图,小明从街道的E处出发,先到F处与小红会合,再一起到位于G处的老年公寓参加志愿者活动,则小明到老年公寓可以选择的最短路径条数为( )
A.24
B.18
C.12
D.9
6.给一些书编号,准备用3个字符,其中首字符用A,B,后两个字符用a,b,c(允许重复),则不同编号的书共有( )
A.8本 B.9本 C.12本 D.18本
7.由数字1,2,3组成的无重复数字的整数中,偶数的个数为( )
A.15 B.12 C.10 D.5
8.把10个苹果分成三堆,要求每堆至少有1个,至多5个,则不同的分法共有( )
A.4种 B.5种 C.6种 D.7种
9.三人踢毽子,互相传递,每人每次只能踢一下.由甲开始踢,经过4次传递后,毽子又被踢回甲,则不同的传递方式共有( )
A.4种 B.5种 C.6种 D.12种
10.已知集合M={1,-2,3},N={-4,5,6,-7},从两个集合中各取一个元素作为点的坐标,则在直角坐标系中,第一、二象限不同点的个数为( )
A.18 B.16 C.14 D.10
11.用4种不同的颜色涂入图中的矩形A,B,C,D中,要求相邻的矩形涂色不同,
则不同的涂色方法共有( )
A.12种 B.24种 C.48种 D.72种
12.如图,某电子器件是由三个电阻组成的回路,其中共有6个焊接点A,B,C,D,
E,F,如果某个焊接点脱落,整个电路就会不通,现在电路不通了,那么焊接点
脱落的可能性共有( )
A.6种 B.36种 C.63种 D.64种
13.将三封信投入四个信箱,可能的投放方法共有种( )
A.7 B.12 C.64 D.81
14.将1,2,3,…,9这9个数字填在如图的9个空格中,要求每一行从左到右,每一列从上到下分别依次增大.当3,4固定在图中的位置时,填写空格的方法为( )
3 4
A.6种 B.12种 C.18种 D.24种
15.某团支部进行换届选举,从甲、乙、丙、丁四人中选出三人分别担任书记、副书记、组织委员,规定上届任职的甲、乙、丙三人不能连任原职,则不同的任职方案有( )
A.10 B.11 C.12 D.13
16.在夏季,一个女生有红、绿、黄3件上衣,红、绿、黄、白、黑5条裙子,这个女生夏季某一天去学校上学,不同的穿法有( ).
A.8种 B.15种 C.种 D.种
17.用0到9这10个数字,可以组成没有重复数字的三位偶数( )
A.256 B.280 C.306 D.328
18.小红把英语单词“babby”中字母的拼写顺序写错了,则她可能出现的错误种数是( )
A.20 B.10 C.19 D.9
19.高三年级的三个班去甲、乙、丙、丁四个工厂参加社会实践,甲工厂必须有班级要去,去何工厂自由选择,则不同的分配方案有( )
A.16种 B.18种 C.37种 D.48种
20.甲、乙、丙三人传球,由甲开始发球,并作为第1次传球,经过5次传球后,球仍回到甲手中,则不同的传球方式共有( )
A.6 B.8 C.10 D.12
21.下表为第29届奥运会奖牌榜前10名:
设表示从“金牌、银牌、铜牌、总数”4项中任取不同两项构成的一个排列,按下面的方式对10个国家进行排名:首先按由大至小排序(表格中从上至下),若值相同,则按值由大至小排序,若值也相同,则顺序任意,那么在所有的排序中,中国的排名之和是( )
A.15 B.20 C.24 D.27
二、填空题:
22.如图所示,在A,B间有四个焊接点,若焊接点脱落,则可能导致电路不通.
今发现A,B之间线路不通,则焊接点脱落的不同情况有________种.
23.将4种蔬菜种植在如图所示的5块试验田里,每块试验田种植一种蔬菜,
相邻试验田不能种植同一种蔬菜,不同的种法有________种.(种植品种可以不全)
24.某班新年联欢晚会原定的5个节目已排成节目单,开演前又增加了两个新节目,如果将这2个节目插入原节目单中,那么有______ 种不同的插法
25.古人用天干、地支来表示年、月、日、时的次序.用天干的“甲、丙、戊、庚、壬”和地支的“子、寅、辰、午、申、戌”相配,用天干的“乙、丁、己、辛、癸”和地支的“丑、卯、巳、未、酉、亥”相配,共可配成______组.
三、解答题
26.某外语组有9人,每人至少会英语和日语中的一门,其中7人会英语,3人会日语,从中选出会英语和日语的各一人,有多少种不同的选法?
27.现有高一四个班的学生34人,其中一、二、三、四班分别有7人、8人、9人、10人,他们自愿组成数学课外小组.
(1)选其中一人为负责人,有多少种不同的选法?
(2)每班选一名组长,有多少种不同的选法?
(3)推选两人做中心发言,这两人需来自不同的班级,有多少种不同的选法?
答案:
二、填空题22-——25 13 42 42 60
三、解答题
26. 由题意,某外语组有9人,其中7人会英语,3人会日语,
则英语和日语都会的有7+3-9=1人
则只会英语的有6人,只会日语的有2人,
以只会英语的人被不被抽到,分2类讨论,假设这个人代号为A
①不选A,有6×2=12种选法
②选A为英语,则有1×2=2种选法
③选A为日语,有6×1=6种选法
综上共有20种选法
答:有20种不同的选法
27. (1)分四类:第一类,从bai一班学生中选1人,有7种选法;
第二类,从二班学生中选1人,有8种选法;
第三类,从三班学生中选1人,有9种选法;
第四类,从四班学生中选1人,有10种选法.
所以共有不同的选法N=7+8+9+10=34????????????????????????????
(2)分四步,第一、二、三、四步分别从一、二、三、四班学生中选一人任组长,所以共有不同的选法N=7×8×9×10="5" 040
(3)分六类,每类又分两步,从一、二班学生中各选1人,有7×8种不同的选法;从一、三班学生中各选1人,有7×9种不同的选法;从一、四班学生中各选1人,有7×10种不同的选法;从二、三班学生中各选1人,有8×9种不同的选法;从二、四班学生中各选1人,有8×10种不同的选法;从三、四班学生中各选1人,有9×10种不同的选法,
所以共有不同的选法
N=7×8+7×9+7×10+8×9+8×10+9×10=431(种)
计数原理
编号:098
一、选择题:
1.从甲地到乙地一天有汽车8班,火车3班,轮船2班,某人从甲地到乙地,他共有不同的走法数为( )
A.13种 B.16种 C.24种 D.48种
2.已知x∈{2,3,7},y∈{-31,-24,4},则(x,y)可表示不同的点的个数是( )
A.1 B.3 C.6 D.9
3.甲、乙两人从4门课程中各选修1门,则甲、乙所选的课程不相同的选法共有( )
A.6种 B.12种 C.30种 D.36种
4.两条异面直线a,b上分别有5个点和8个点,则这13个点可以确定不同的平面个数为( )
A.40 B.16 C.13 D.10
5.如图,小明从街道的E处出发,先到F处与小红会合,再一起到位于G处的老年公寓参加志愿者活动,则小明到老年公寓可以选择的最短路径条数为( )
A.24
B.18
C.12
D.9
6.给一些书编号,准备用3个字符,其中首字符用A,B,后两个字符用a,b,c(允许重复),则不同编号的书共有( )
A.8本 B.9本 C.12本 D.18本
7.由数字1,2,3组成的无重复数字的整数中,偶数的个数为( )
A.15 B.12 C.10 D.5
8.把10个苹果分成三堆,要求每堆至少有1个,至多5个,则不同的分法共有( )
A.4种 B.5种 C.6种 D.7种
9.三人踢毽子,互相传递,每人每次只能踢一下.由甲开始踢,经过4次传递后,毽子又被踢回甲,则不同的传递方式共有( )
A.4种 B.5种 C.6种 D.12种
10.已知集合M={1,-2,3},N={-4,5,6,-7},从两个集合中各取一个元素作为点的坐标,则在直角坐标系中,第一、二象限不同点的个数为( )
A.18 B.16 C.14 D.10
11.用4种不同的颜色涂入图中的矩形A,B,C,D中,要求相邻的矩形涂色不同,
则不同的涂色方法共有( )
A.12种 B.24种 C.48种 D.72种
12.如图,某电子器件是由三个电阻组成的回路,其中共有6个焊接点A,B,C,D,
E,F,如果某个焊接点脱落,整个电路就会不通,现在电路不通了,那么焊接点
脱落的可能性共有( )
A.6种 B.36种 C.63种 D.64种
13.将三封信投入四个信箱,可能的投放方法共有种( )
A.7 B.12 C.64 D.81
14.将1,2,3,…,9这9个数字填在如图的9个空格中,要求每一行从左到右,每一列从上到下分别依次增大.当3,4固定在图中的位置时,填写空格的方法为( )
3 4
A.6种 B.12种 C.18种 D.24种
15.某团支部进行换届选举,从甲、乙、丙、丁四人中选出三人分别担任书记、副书记、组织委员,规定上届任职的甲、乙、丙三人不能连任原职,则不同的任职方案有( )
A.10 B.11 C.12 D.13
16.在夏季,一个女生有红、绿、黄3件上衣,红、绿、黄、白、黑5条裙子,这个女生夏季某一天去学校上学,不同的穿法有( ).
A.8种 B.15种 C.种 D.种
17.用0到9这10个数字,可以组成没有重复数字的三位偶数( )
A.256 B.280 C.306 D.328
18.小红把英语单词“babby”中字母的拼写顺序写错了,则她可能出现的错误种数是( )
A.20 B.10 C.19 D.9
19.高三年级的三个班去甲、乙、丙、丁四个工厂参加社会实践,甲工厂必须有班级要去,去何工厂自由选择,则不同的分配方案有( )
A.16种 B.18种 C.37种 D.48种
20.甲、乙、丙三人传球,由甲开始发球,并作为第1次传球,经过5次传球后,球仍回到甲手中,则不同的传球方式共有( )
A.6 B.8 C.10 D.12
21.下表为第29届奥运会奖牌榜前10名:
设表示从“金牌、银牌、铜牌、总数”4项中任取不同两项构成的一个排列,按下面的方式对10个国家进行排名:首先按由大至小排序(表格中从上至下),若值相同,则按值由大至小排序,若值也相同,则顺序任意,那么在所有的排序中,中国的排名之和是( )
A.15 B.20 C.24 D.27
二、填空题:
22.如图所示,在A,B间有四个焊接点,若焊接点脱落,则可能导致电路不通.
今发现A,B之间线路不通,则焊接点脱落的不同情况有________种.
23.将4种蔬菜种植在如图所示的5块试验田里,每块试验田种植一种蔬菜,
相邻试验田不能种植同一种蔬菜,不同的种法有________种.(种植品种可以不全)
24.某班新年联欢晚会原定的5个节目已排成节目单,开演前又增加了两个新节目,如果将这2个节目插入原节目单中,那么有______ 种不同的插法
25.古人用天干、地支来表示年、月、日、时的次序.用天干的“甲、丙、戊、庚、壬”和地支的“子、寅、辰、午、申、戌”相配,用天干的“乙、丁、己、辛、癸”和地支的“丑、卯、巳、未、酉、亥”相配,共可配成______组.
三、解答题
26.某外语组有9人,每人至少会英语和日语中的一门,其中7人会英语,3人会日语,从中选出会英语和日语的各一人,有多少种不同的选法?
27.现有高一四个班的学生34人,其中一、二、三、四班分别有7人、8人、9人、10人,他们自愿组成数学课外小组.
(1)选其中一人为负责人,有多少种不同的选法?
(2)每班选一名组长,有多少种不同的选法?
(3)推选两人做中心发言,这两人需来自不同的班级,有多少种不同的选法?
答案:
二、填空题22-——25 13 42 42 60
三、解答题
26. 由题意,某外语组有9人,其中7人会英语,3人会日语,
则英语和日语都会的有7+3-9=1人
则只会英语的有6人,只会日语的有2人,
以只会英语的人被不被抽到,分2类讨论,假设这个人代号为A
①不选A,有6×2=12种选法
②选A为英语,则有1×2=2种选法
③选A为日语,有6×1=6种选法
综上共有20种选法
答:有20种不同的选法
27. (1)分四类:第一类,从bai一班学生中选1人,有7种选法;
第二类,从二班学生中选1人,有8种选法;
第三类,从三班学生中选1人,有9种选法;
第四类,从四班学生中选1人,有10种选法.
所以共有不同的选法N=7+8+9+10=34????????????????????????????
(2)分四步,第一、二、三、四步分别从一、二、三、四班学生中选一人任组长,所以共有不同的选法N=7×8×9×10="5" 040
(3)分六类,每类又分两步,从一、二班学生中各选1人,有7×8种不同的选法;从一、三班学生中各选1人,有7×9种不同的选法;从一、四班学生中各选1人,有7×10种不同的选法;从二、三班学生中各选1人,有8×9种不同的选法;从二、四班学生中各选1人,有8×10种不同的选法;从三、四班学生中各选1人,有9×10种不同的选法,
所以共有不同的选法
N=7×8+7×9+7×10+8×9+8×10+9×10=431(种)
