2020-2021学年华东师大新版九年级下册数学期中复习试卷1(word含解析)
文档属性
| 名称 | 2020-2021学年华东师大新版九年级下册数学期中复习试卷1(word含解析) |
|
|
| 格式 | zip | ||
| 文件大小 | 579.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-04-18 00:00:00 | ||
图片预览


文档简介
2020-2021学年华东师大新版九年级下册数学期中复习试卷1
一.选择题(共10小题,满分40分,每小题4分)
1.在﹣1,0,2,四个数中,最大的数是( )
A.﹣1
B.0
C.2
D.
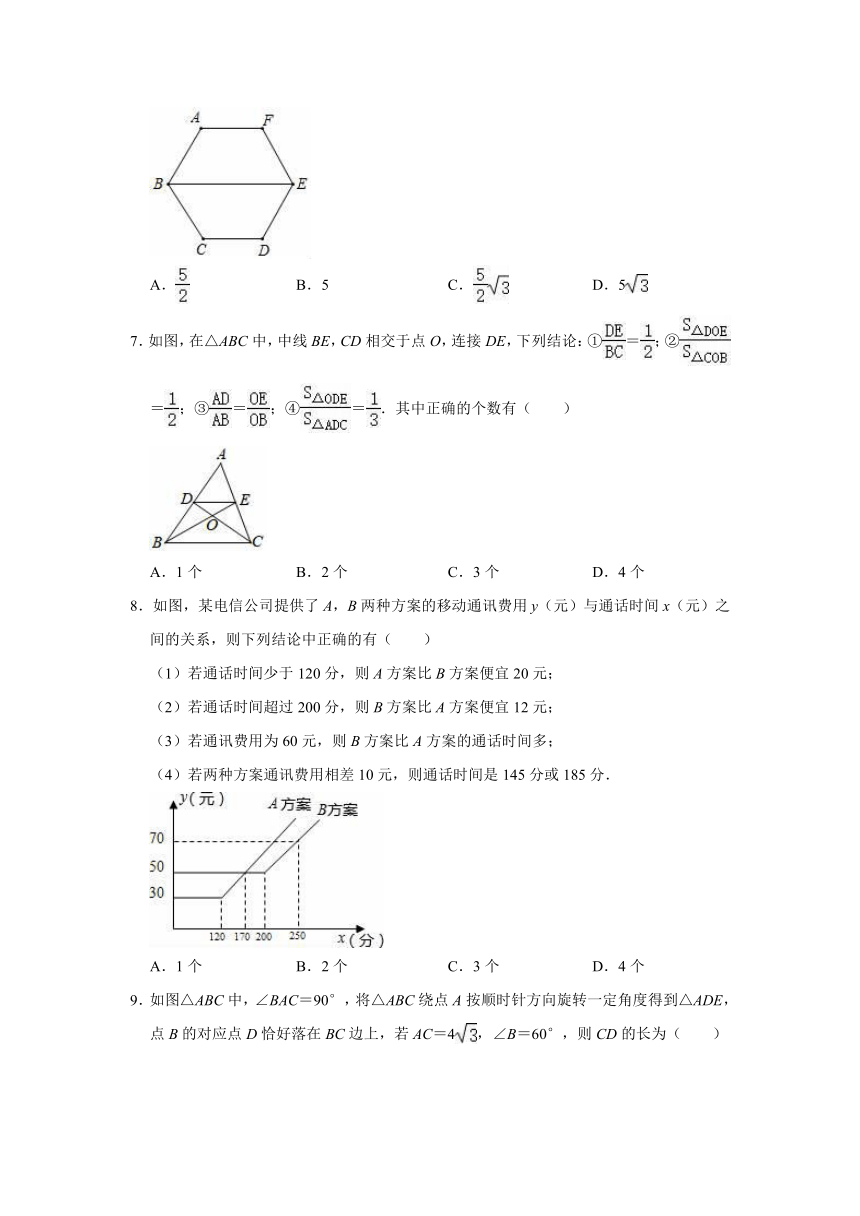
2.如图所示的几何体的左视图是( )
A.
B.
C.
D.
3.地球的表面积约为510000000km2,将510000000用科学记数法表示为( )
A.0.51×109
B.5.1×108
C.5.1×109
D.51×107
4.下列手机手势解锁图案中,是中心对称图形的是( )
A.
B.
C.
D.
5.下列说法正确的是( )
A.打开电视机,正在播放“张家界新闻”是必然事件
B.天气预报说“明天的降水概率为65%”,意味着明天一定下雨
C.两组数据平均数相同,则方差大的更稳定
D.数据5,6,7,7,8的中位数与众数均为7
6.在正六边形ABCDEF的中,若BE=10,则这个正六边形外接圆半径是( )
A.
B.5
C.
D.5
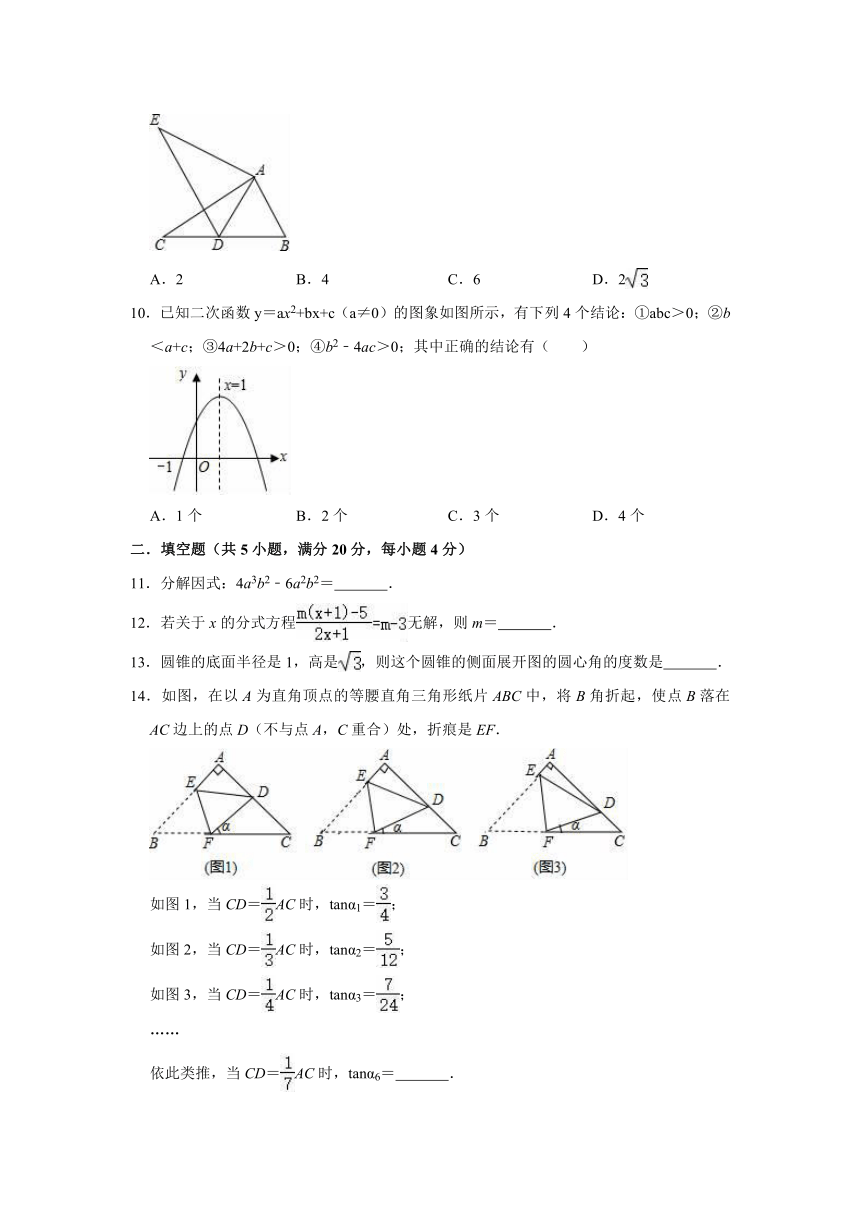
7.如图,在△ABC中,中线BE,CD相交于点O,连接DE,下列结论:①=;②=;③=;④=.其中正确的个数有( )
A.1个
B.2个
C.3个
D.4个
8.如图,某电信公司提供了A,B两种方案的移动通讯费用y(元)与通话时间x(元)之间的关系,则下列结论中正确的有( )
(1)若通话时间少于120分,则A方案比B方案便宜20元;
(2)若通话时间超过200分,则B方案比A方案便宜12元;
(3)若通讯费用为60元,则B方案比A方案的通话时间多;
(4)若两种方案通讯费用相差10元,则通话时间是145分或185分.
A.1个
B.2个
C.3个
D.4个
9.如图△ABC中,∠BAC=90°,将△ABC绕点A按顺时针方向旋转一定角度得到△ADE,点B的对应点D恰好落在BC边上,若AC=4,∠B=60°,则CD的长为( )
A.2
B.4
C.6
D.2
10.已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,有下列4个结论:①abc>0;②b<a+c;③4a+2b+c>0;④b2﹣4ac>0;其中正确的结论有( )
A.1个
B.2个
C.3个
D.4个
二.填空题(共5小题,满分20分,每小题4分)
11.分解因式:4a3b2﹣6a2b2=
.
12.若关于x的分式方程无解,则m=
.
13.圆锥的底面半径是1,高是,则这个圆锥的侧面展开图的圆心角的度数是
.
14.如图,在以A为直角顶点的等腰直角三角形纸片ABC中,将B角折起,使点B落在AC边上的点D(不与点A,C重合)处,折痕是EF.
如图1,当CD=AC时,tanα1=;
如图2,当CD=AC时,tanα2=;
如图3,当CD=AC时,tanα3=;
……
依此类推,当CD=AC时,tanα6=
.
15.设a,b是实数,定义@的一种运算如下:a@b=(a+b)2﹣(a﹣b)2,则下列结论:
①若a@b=0,则a=0或b=0;②a@(b+c)=a@b+a@c;
③不存在实数a,b,满足a@b=a2+5b2;
④设a,b是矩形的长和宽,若矩形的周长固定,则当a=b时,a@b最大.
其中正确的是
.
三.解答题(共11小题,满分90分)
16.(5分)计算:﹣|﹣2|+sin60°﹣(﹣)﹣1+(π﹣3.14)0.
17.(6分)先化简,再求值:(x﹣2+)÷,其中x=﹣.
18.(6分)已知关于x的方程x2+ax+a﹣2=0
(1)求证:不论a取何实数,该方程都有两个不相等的实数根;
(2)若该方程的一个根为1,求a的值及该方程的另一根.
19.(8分)我市创全国卫生城市,某街道积极响应,决定在街道内的所有小区安装垃圾分类的温馨提示牌和垃圾箱,若购买4个垃圾箱比购买5个温馨提示牌多350元,垃圾箱的单价是温馨提示牌单价的3倍.
(1)求温馨提示牌和垃圾箱的单价各是多少元?
(2)如果该街道需购买温馨提示牌和垃圾箱共3000个.
①求购买温馨提示牌和垃圾箱所需费用w(元)与温馨提示牌的个数x的函数关系式;
②若该街道计划费用不超过35万元,而且垃圾箱的个数不少于温馨提示牌的个数的1.5倍,求有几种可供选择的方案?并找出资金最少的方案,求出最少需多少元?
20.(8分)如图,点C,F,E,B在一条直线上,∠CFD=∠BEA,CE=BF,DF=AE,写出CD与AB之间的关系,并证明你的结论.
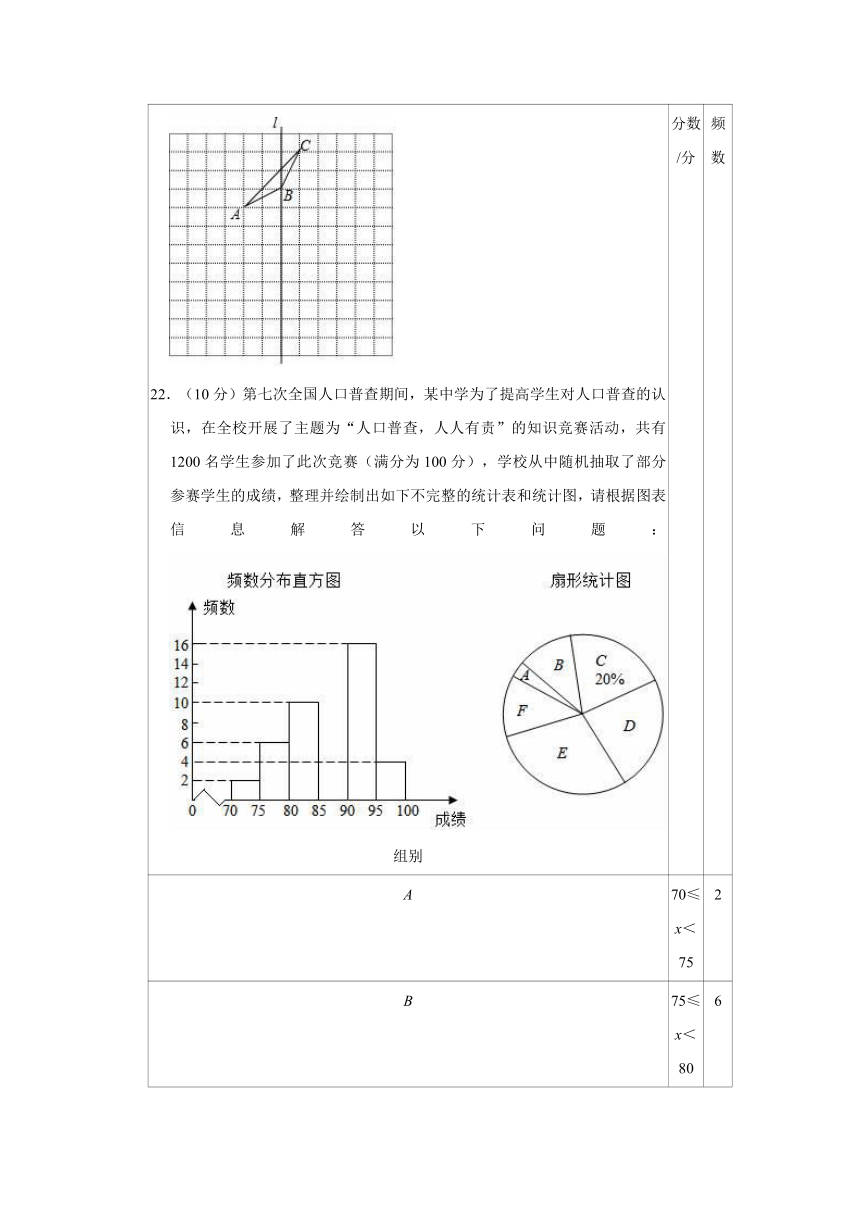
21.(8分)如图,在由边长为1个单位长度的小正方形组成的12×12网格中,给出了格点△ABC和直线l.
(1)画出△ABC关于直线l对称的格点△A′B′C;
(2)在直线l上选取一格点,在网格内画出格点△DPE,使得△DPE∽△ABC,且相似比为2:1.
22.(10分)第七次全国人口普查期间,某中学为了提高学生对人口普查的认识,在全校开展了主题为“人口普查,人人有责”的知识竞赛活动,共有1200名学生参加了此次竞赛(满分为100分),学校从中随机抽取了部分参赛学生的成绩,整理并绘制出如下不完整的统计表和统计图,请根据图表信息解答以下问题:组别
分数/分
频数
A
70≤x<75
2
B
75≤x<80
6
C
80≤x<85
10
D
85≤x<90
a
E
90≤x<95
16
F
95≤x≤100
4
(1)本次调查随机抽取了
个参赛学生的成绩;所抽取参赛学生成绩的中位数所在的“组别”是
;
(2)补全频数分布直方图;
(3)估计全校1200名学生中,知识竞赛成绩达到“优秀(90≤x≤100)”的有
名;
(4)成绩前四名的学生中有两名男生和两名女生,若从这四名学生中选两人为该校的人口普查知识宣传员,求恰好选中一名男生和一名女生的概率.
23.(10分)九年级某数学兴趣小组在学习了反比例函数的图象与性质后,进一步研究了函数y=的图象与性质,其探究过程如下:
(1)绘制函数图象,如图1.
列表:下表是x与y的几组对应值,其中m=
;
x
…
﹣3
﹣2
﹣1
﹣
1
2
3
…
y
…
1
2
4
4
2
m
…
描点:根据表中各组对应值(x,y),在平面直角坐标系中描出了各点;
连线:用平滑的曲线顺次连接各点,画出了部分图象.请你把图象补充完整;
(2)通过观察图1,写出该函数的两条性质;
①
;
②
;
(3)①观察发现:如图2.若直线y=2交函数y=的图象于A,B两点,连接OA,过点B作BC∥OA交x轴于C.则S四边形OABC=
;
②探究思考:将①中“直线y=2”改为“直线y=a(a>0)”,其他条件不变,则S四边形OABC=
;
③类比猜想:若直线y=a(a>0)交函数y=(k>0)的图象于A,B两点,连接OA,过点B作BC∥OA交x轴于C,则S四边形OABC=
.
24.(8分)如图,小亮在大楼AD的观光电梯中的E点测得大楼BC楼底C点的俯角为60°,此时他距地面的高度AE为21米,电梯再上升9米到达D点,此时测得大楼BC楼顶B点的仰角为45°,求大楼BC的高度.(结果保留根号)
25.(9分)如图,AC是⊙O的直径,点B是⊙O上一点,且BD=BA,过点B作BE⊥DC,交DC的延长线于点E.
(1)求证:BE是⊙O的切线;
(2)若BE=2CE,当AD=6时,求BD的长.
26.(12分)已知抛物线与x轴交于点A(﹣2,0)、B(3,0),与y轴交于点C(0,4).
(1)求抛物线的解析式;
(2)如图1,点P是抛物线上位于第一象限内的一点,当四边形ABPC的面积最大时,求出四边形ABPC的面积最大值及此时点P的坐标.
(3)如图2,将抛物线向右平移个单位,再向下平移2个单位.记平移后的抛物线为y',若抛物线y'与原抛物线对称轴交于点Q.点E是新抛物线y'对称轴上一动点,在(2)的条件下,当△PQE是等腰三角形时,求点E的坐标.
参考答案与试题解析
一.选择题(共10小题,满分40分,每小题4分)
1.解:根据实数比较大小的方法,可得
﹣1<0<<2,
∴在:﹣1,0,2,四个数中,最大的数是2.
故选:C.
2.解:从左边看,是一个正方形,正方形的右上角有一条虚线.
故选:B.
3.解:510000000=5.1×108,
故选:B.
4.解:A、不是中心对称图形;
B、是中心对称图形;
C、不是中心对称图形;
D、不是中心对称图形.
故选:B.
5.解:A.打开电视机,正在播放“张家界新闻”是随机事件,故A错误;
B.天气预报说“明天的降水概率为65%”,意味着明天可能下雨,故B错误;
C.两组数据平均数相同,则方差大的更不稳定,故C错误;
D,数据5,6,7,7,8的中位数与众数均为7,正确.
故选:D.
6.解:因为正六边形ABCDEF的中,BE=10,
所以这个正六边形外接圆半径是,
故选:B.
7.解:∵CD、BE为△ABC的中线,
∴DE为△ABC的中位线,
∴DE=BC,所以①正确;
DE∥BC;
∴△DOE∽△COB,
∴=()2=,所以②错误;
∵中线BE,CD相交于点O,
∴O点为△ABC的重心,
∴OB=2OE,
而AB=2AD,
∴==,所以③正确;
∵O点为△ABC的重心,
∴OC=2OD,
∴S△ODE=S△CDE,
∵AE=CE,
∴S△CDE=S△ADC,
∴S△DOE=S△ADC,所以④错误.
故选:B.
8.解:依题意得
A:(1)当0≤x≤120,yA=30,
(2)当x>120,yA=30+(x﹣120)×[(50﹣30)÷(170﹣120)]=0.4x﹣18;
B:(1)当0≤x<200,yB=50,
当x>200,yB=50+[(70﹣50)÷(250﹣200)](x﹣200)=0.4x﹣30,
所以当x≤120时,A方案比B方案便宜20元,故(1)正确;
当x≥200时,B方案比A方案便宜12元,故(2)正确;
当y=60时,A:60=0.4x﹣18,∴x=195,
B:60=0.4x﹣30,∴x=225,故(3)正确;
当B方案为50元,A方案是40元或者60元时,两种方案通讯费用相差10元,
将yA=40或60代入,得x=145分或195分,故(4)错误;
故选:C.
9.解:在Rt△ABC中,AC=4,∠B=60°,
∴AB=4,BC=8,
由旋转得,AD=AB,
∵∠B=60°,
∴BD=AB=4,
∴CD=BC﹣BD=8﹣4=4,
故选:B.
10.解:①∵抛物线开口向下,
∴a<0.
∵抛物线的对称轴为x=﹣=1,
∴b=﹣2a>0.
当x=0时,y=c>0,
∴abc<0,①错误;
②当x=﹣1时,y<0,
∴a﹣b+c<0,
∴b>a+c,②错误;
③∵抛物线的对称轴为x=1,
∴当x=2时与x=0时,y值相等,
∵当x=0时,y=c>0,
∴4a+2b+c=c>0,③正确;
④∵抛物线与x轴有两个不相同的交点,
∴一元二次方程ax2+bx+c=0,
∴△=b2﹣4ac>0,④正确.
综上可知:成立的结论有2个.
故选:B.
二.填空题(共5小题,满分20分,每小题4分)
11.解:4a3b2﹣6a2b2=2a2b2(2a﹣3).
故答案为:2a2b2(2a﹣3).
12.解:∵关于x的分式方程无解,
∴x=﹣,
原方程去分母得:m(x+1)﹣5=(2x+1)(m﹣3)
解得:x=,m=6时,方程无解.
或=﹣是方程无解,此时m=10.
故答案为6,10.
13.解:设圆锥的母线为a,根据勾股定理得,a=2,
设圆锥的侧面展开图的圆心角度数为n°,
根据题意得2π?1=,解得n=180,
即圆锥的侧面展开图的圆心角度数为180°.
故答案为180°.
14.解:根据规律可得,
当n=2时,CD=AC,tanα1==
当n=3时,CD=AC,tanα2==,
当n=4时,CD=AC,tanα3==,
………………
当n=7时,CD=AC,tanα6==,
故答案为:.
15.解:①根据题意得:a@b=(a+b)2﹣(a﹣b)2
∴(a+b)2﹣(a﹣b)2=0,
整理得:(a+b+a﹣b)(a+b﹣a+b)=0,即4ab=0,
解得:a=0或b=0,正确;
②∵a@(b+c)=(a+b+c)2﹣(a﹣b﹣c)2=4ab+4ac
a@b+a@c=(a+b)2﹣(a﹣b)2+(a+c)2﹣(a﹣c)2=4ab+4ac,
∴a@(b+c)=a@b+a@c,正确;
③∵a@b=a2+5b2,a@b=(a+b)2﹣(a﹣b)2=4ab,
∴a2+5b2=4ab,
∴a2﹣4ab+5b2=0,
∴(a﹣2b)2+b2=0,
∴,
∴,
故错误;
④∵a@b=(a+b)2﹣(a﹣b)2=4ab,
(a﹣b)2≥0,则a2﹣2ab+b2≥0,即a2+b2≥2ab,
∴a2+b2+2ab≥4ab,
∴4ab的最大值是a2+b2+2ab,此时a2+b2+2ab=4ab,
解得a=b,
∴a@b最大时,a=b,故④正确.
故答案为:①②④.
三.解答题(共11小题,满分90分)
16.解:原式=﹣2+2×+2+1,
=﹣2+3+2+1,
=4.
17.解:原式=(+)?
=?
=2(x+2)
=2x+4,
当x=﹣时,
原式=2×(﹣)+4
=﹣1+4
=3.
18.解:(1)∵△=a2﹣4(a﹣2)=a2﹣4a+8=a2﹣4a+4+4=(a﹣2)2+4>0,
∴不论a取何实数,该方程都有两个不相等的实数根;
(2)将x=1代入方程x2+ax+a﹣2=0得,1+a+a﹣2=0,解得a=;
方程为x2+x﹣=0,即2x2+x﹣3=0,
设另一根为x1,则
1?x1=﹣,
解得x1=﹣.
19.解:(1)设温馨提示牌的单价为a元,
4×3a﹣5a=350
解得:a=50,
则3a=150,
答:温馨提示牌、垃圾箱的单价分别为50元和150元;
(2)①由题意可得,
w=50x+150(3000﹣x)=﹣100x+450000,
即购买温馨提示牌和垃圾箱所需费用w(元)与温馨提示牌的个数x的函数关系式是:w=﹣100x+450000;
②由题意得,
,
解得:1000≤x≤1200,
∵x为整数,
∴共有201种可供选择的方案,
∵k=﹣100<0,w随x的增大而减小,
∴当x=1200时,w取得最少值,此时w=330000元,3000﹣x=1800,
答:有201种可供选择的方案,其中购买温馨提示牌1200个,垃圾桶1800个时所需资金最少,最少为330000元.
20.解:CD∥AB,CD=AB,
理由是:∵CE=BF,
∴CE﹣EF=BF﹣EF,
∴CF=BE,
在△AEB和△CFD中,
,
∴△AEB≌△CFD(SAS),
∴CD=AB,∠C=∠B,
∴CD∥AB.
21.解:(1)如图所示:△A′B′C′即为所求;
(2)如图所示:△DPE即为所求.
22.解:(1)10÷20%=50(个),则a=50﹣2﹣6﹣10﹣16﹣4=12,
所抽取参赛学生成绩的中位数是第25个、第26个参赛学生成绩的平均数,
∴所抽取参赛学生成绩的中位数所在的“组别”是D,
故答案为:50,D;
(2)补全频数分布直方图如下:
(3)1200×=480(名),
即估计全校1200名学生中,知识竞赛成绩达到“优秀(90≤x≤100)”的有480名,
故答案为:480;
(4)画树状图如图:
共有12个等可能的结果,恰好选中一名男生和一名女生的结果有8个,
∴恰好选中一名男生和一名女生的概率为=.
23.解:(1)当x<0时,xy=﹣2,而当x>0时,xy=2,
∴m=1,
故答案为:1;补全图象如图所示:
(2)由函数图象的对称性可知,函数的图象关于y轴对称,
从函数的增减性可知,在y轴的左侧(x<0),y随x的增大而增大;在y轴的右侧(x>0),y随x的增大而减小;
故答案为:①函数的图象关于y轴对称,②当x<0时,y随x的增大而增大,当x>0时,y随x的增大而减小;
(3)如图,①由A,B两点关于y轴对称,由题意可得四边形OABC是平行四边形,且S四边形OABC=4S△OAM=4×|k|=2|k|=4,
②同①可知:S四边形OABC=2|k|=4,
③S四边形OABC=2|k|=2k,
故答案为:4,4,2k.
24.解:过D作DH⊥BC于H,过E作EG⊥BC于G.
由已知得,∠BDH=45°,∠CEG=60°,AE=21米,DE=9米.
在Rt△CEG中,CG=AE=21米,tan∠CEG=,
∴EG===7(米).
∴DH=EG=7米.
在Rt△BDH中,∵∠BDH=45°,
∴BH=DH=7米.
∴BC=CG+HG+BH=CG+DE+BH=21+9+7=(30+7)米.
答:大楼BC的高度是(30+7)米.
25.(1)证明:连接OB、OD,如图1所示:
∵AB=DB,AO=DO,BO=BO,
∴△ABO≌△DBO(SSS),
∴∠ABO=∠DBO,
∵OA=OB,∠BDC=∠BAC,
∴∠ABO=∠BAC=∠BDC,
∴∠DBO=∠BDC,
∴OB∥DE,
∵BE⊥DC,
∴BE⊥OB,
∴BE是⊙O的切线;
(2)解:延长BO交AD于点F,如图2所示:
由(1)可知,∠ABO=∠DBO,
∵AB=BD,
∴BF⊥AD,AF=DF=AD=3,
∵∠BAF=∠BCE,∠AFB=∠E=90°,BE=2CE,
∴△ABF∽△CBE,
∴==2,
∴BF=2AF=6,
在Rt△ABF中,由勾股定理得:AB===3,
∴BD=AB=3.
26.解:(1)∵抛物线与x轴交于点A(﹣2,0)、B(3,0),
∴可设抛物线的解析式为:y=a(x+2)(x﹣3)(a≠0),
把C(0,4)代入y=a(x+2)(x﹣3)(a≠0)中,得
4=﹣6a,
∴a=﹣,
∴抛物线的解析式为:y=﹣,
即y=﹣+;
(2)设P点的坐标为(t,),过点P作PM⊥x轴,与BC交于点M,如图1,
设直线BC的解析式为y=kx+b(k≠0),则
,
解得,
∴直线BC的解析式为:y=﹣,
∴M(t,),
∴,
∴=﹣t2+3t,
,
,
∴S四边形ABPC=S△AOC+S△BOC+S△BPC=,
∴当t=时,S四边形ABPC的最大值为,
∴此时P点的坐标为(,);
(3)∵将抛物线向右平移个单位,再向下平移2个单位.记平移后的抛物线为y',
∴y′的解析式为y′=﹣(x﹣)2+(x﹣)+4﹣2,即y′=﹣x2+x+,
∴抛物线y′的对称轴为x=1,
∵抛物线y=﹣+=﹣(x﹣)2+,
∴抛物线y=﹣+的对称轴为直线x=,
把x=代入y′=﹣x2+x+,中,得y′=2,
∴Q点的坐标为(,2),
设E的坐标为(1,n)
①当PE=QE时,则PE2=QE2,
即,
解得,n=,
∴E(1,),
②当PQ=QE时,则PQ2=QE2,
即,
解得,n=2±,
∴E点的坐标为(1,2+)或(1,2﹣);
③当PQ=PE时,则PQ2=PE2,
即,
解得,n=,
∴点E的坐标为(1,)或(1,).
综上,当△PQE是等腰三角形时,点E的坐标为(1,)或(1,2+)或(1,2﹣)或(1,)或(1,).
一.选择题(共10小题,满分40分,每小题4分)
1.在﹣1,0,2,四个数中,最大的数是( )
A.﹣1
B.0
C.2
D.
2.如图所示的几何体的左视图是( )
A.
B.
C.
D.
3.地球的表面积约为510000000km2,将510000000用科学记数法表示为( )
A.0.51×109
B.5.1×108
C.5.1×109
D.51×107
4.下列手机手势解锁图案中,是中心对称图形的是( )
A.
B.
C.
D.
5.下列说法正确的是( )
A.打开电视机,正在播放“张家界新闻”是必然事件
B.天气预报说“明天的降水概率为65%”,意味着明天一定下雨
C.两组数据平均数相同,则方差大的更稳定
D.数据5,6,7,7,8的中位数与众数均为7
6.在正六边形ABCDEF的中,若BE=10,则这个正六边形外接圆半径是( )
A.
B.5
C.
D.5
7.如图,在△ABC中,中线BE,CD相交于点O,连接DE,下列结论:①=;②=;③=;④=.其中正确的个数有( )
A.1个
B.2个
C.3个
D.4个
8.如图,某电信公司提供了A,B两种方案的移动通讯费用y(元)与通话时间x(元)之间的关系,则下列结论中正确的有( )
(1)若通话时间少于120分,则A方案比B方案便宜20元;
(2)若通话时间超过200分,则B方案比A方案便宜12元;
(3)若通讯费用为60元,则B方案比A方案的通话时间多;
(4)若两种方案通讯费用相差10元,则通话时间是145分或185分.
A.1个
B.2个
C.3个
D.4个
9.如图△ABC中,∠BAC=90°,将△ABC绕点A按顺时针方向旋转一定角度得到△ADE,点B的对应点D恰好落在BC边上,若AC=4,∠B=60°,则CD的长为( )
A.2
B.4
C.6
D.2
10.已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,有下列4个结论:①abc>0;②b<a+c;③4a+2b+c>0;④b2﹣4ac>0;其中正确的结论有( )
A.1个
B.2个
C.3个
D.4个
二.填空题(共5小题,满分20分,每小题4分)
11.分解因式:4a3b2﹣6a2b2=
.
12.若关于x的分式方程无解,则m=
.
13.圆锥的底面半径是1,高是,则这个圆锥的侧面展开图的圆心角的度数是
.
14.如图,在以A为直角顶点的等腰直角三角形纸片ABC中,将B角折起,使点B落在AC边上的点D(不与点A,C重合)处,折痕是EF.
如图1,当CD=AC时,tanα1=;
如图2,当CD=AC时,tanα2=;
如图3,当CD=AC时,tanα3=;
……
依此类推,当CD=AC时,tanα6=
.
15.设a,b是实数,定义@的一种运算如下:a@b=(a+b)2﹣(a﹣b)2,则下列结论:
①若a@b=0,则a=0或b=0;②a@(b+c)=a@b+a@c;
③不存在实数a,b,满足a@b=a2+5b2;
④设a,b是矩形的长和宽,若矩形的周长固定,则当a=b时,a@b最大.
其中正确的是
.
三.解答题(共11小题,满分90分)
16.(5分)计算:﹣|﹣2|+sin60°﹣(﹣)﹣1+(π﹣3.14)0.
17.(6分)先化简,再求值:(x﹣2+)÷,其中x=﹣.
18.(6分)已知关于x的方程x2+ax+a﹣2=0
(1)求证:不论a取何实数,该方程都有两个不相等的实数根;
(2)若该方程的一个根为1,求a的值及该方程的另一根.
19.(8分)我市创全国卫生城市,某街道积极响应,决定在街道内的所有小区安装垃圾分类的温馨提示牌和垃圾箱,若购买4个垃圾箱比购买5个温馨提示牌多350元,垃圾箱的单价是温馨提示牌单价的3倍.
(1)求温馨提示牌和垃圾箱的单价各是多少元?
(2)如果该街道需购买温馨提示牌和垃圾箱共3000个.
①求购买温馨提示牌和垃圾箱所需费用w(元)与温馨提示牌的个数x的函数关系式;
②若该街道计划费用不超过35万元,而且垃圾箱的个数不少于温馨提示牌的个数的1.5倍,求有几种可供选择的方案?并找出资金最少的方案,求出最少需多少元?
20.(8分)如图,点C,F,E,B在一条直线上,∠CFD=∠BEA,CE=BF,DF=AE,写出CD与AB之间的关系,并证明你的结论.
21.(8分)如图,在由边长为1个单位长度的小正方形组成的12×12网格中,给出了格点△ABC和直线l.
(1)画出△ABC关于直线l对称的格点△A′B′C;
(2)在直线l上选取一格点,在网格内画出格点△DPE,使得△DPE∽△ABC,且相似比为2:1.
22.(10分)第七次全国人口普查期间,某中学为了提高学生对人口普查的认识,在全校开展了主题为“人口普查,人人有责”的知识竞赛活动,共有1200名学生参加了此次竞赛(满分为100分),学校从中随机抽取了部分参赛学生的成绩,整理并绘制出如下不完整的统计表和统计图,请根据图表信息解答以下问题:组别
分数/分
频数
A
70≤x<75
2
B
75≤x<80
6
C
80≤x<85
10
D
85≤x<90
a
E
90≤x<95
16
F
95≤x≤100
4
(1)本次调查随机抽取了
个参赛学生的成绩;所抽取参赛学生成绩的中位数所在的“组别”是
;
(2)补全频数分布直方图;
(3)估计全校1200名学生中,知识竞赛成绩达到“优秀(90≤x≤100)”的有
名;
(4)成绩前四名的学生中有两名男生和两名女生,若从这四名学生中选两人为该校的人口普查知识宣传员,求恰好选中一名男生和一名女生的概率.
23.(10分)九年级某数学兴趣小组在学习了反比例函数的图象与性质后,进一步研究了函数y=的图象与性质,其探究过程如下:
(1)绘制函数图象,如图1.
列表:下表是x与y的几组对应值,其中m=
;
x
…
﹣3
﹣2
﹣1
﹣
1
2
3
…
y
…
1
2
4
4
2
m
…
描点:根据表中各组对应值(x,y),在平面直角坐标系中描出了各点;
连线:用平滑的曲线顺次连接各点,画出了部分图象.请你把图象补充完整;
(2)通过观察图1,写出该函数的两条性质;
①
;
②
;
(3)①观察发现:如图2.若直线y=2交函数y=的图象于A,B两点,连接OA,过点B作BC∥OA交x轴于C.则S四边形OABC=
;
②探究思考:将①中“直线y=2”改为“直线y=a(a>0)”,其他条件不变,则S四边形OABC=
;
③类比猜想:若直线y=a(a>0)交函数y=(k>0)的图象于A,B两点,连接OA,过点B作BC∥OA交x轴于C,则S四边形OABC=
.
24.(8分)如图,小亮在大楼AD的观光电梯中的E点测得大楼BC楼底C点的俯角为60°,此时他距地面的高度AE为21米,电梯再上升9米到达D点,此时测得大楼BC楼顶B点的仰角为45°,求大楼BC的高度.(结果保留根号)
25.(9分)如图,AC是⊙O的直径,点B是⊙O上一点,且BD=BA,过点B作BE⊥DC,交DC的延长线于点E.
(1)求证:BE是⊙O的切线;
(2)若BE=2CE,当AD=6时,求BD的长.
26.(12分)已知抛物线与x轴交于点A(﹣2,0)、B(3,0),与y轴交于点C(0,4).
(1)求抛物线的解析式;
(2)如图1,点P是抛物线上位于第一象限内的一点,当四边形ABPC的面积最大时,求出四边形ABPC的面积最大值及此时点P的坐标.
(3)如图2,将抛物线向右平移个单位,再向下平移2个单位.记平移后的抛物线为y',若抛物线y'与原抛物线对称轴交于点Q.点E是新抛物线y'对称轴上一动点,在(2)的条件下,当△PQE是等腰三角形时,求点E的坐标.
参考答案与试题解析
一.选择题(共10小题,满分40分,每小题4分)
1.解:根据实数比较大小的方法,可得
﹣1<0<<2,
∴在:﹣1,0,2,四个数中,最大的数是2.
故选:C.
2.解:从左边看,是一个正方形,正方形的右上角有一条虚线.
故选:B.
3.解:510000000=5.1×108,
故选:B.
4.解:A、不是中心对称图形;
B、是中心对称图形;
C、不是中心对称图形;
D、不是中心对称图形.
故选:B.
5.解:A.打开电视机,正在播放“张家界新闻”是随机事件,故A错误;
B.天气预报说“明天的降水概率为65%”,意味着明天可能下雨,故B错误;
C.两组数据平均数相同,则方差大的更不稳定,故C错误;
D,数据5,6,7,7,8的中位数与众数均为7,正确.
故选:D.
6.解:因为正六边形ABCDEF的中,BE=10,
所以这个正六边形外接圆半径是,
故选:B.
7.解:∵CD、BE为△ABC的中线,
∴DE为△ABC的中位线,
∴DE=BC,所以①正确;
DE∥BC;
∴△DOE∽△COB,
∴=()2=,所以②错误;
∵中线BE,CD相交于点O,
∴O点为△ABC的重心,
∴OB=2OE,
而AB=2AD,
∴==,所以③正确;
∵O点为△ABC的重心,
∴OC=2OD,
∴S△ODE=S△CDE,
∵AE=CE,
∴S△CDE=S△ADC,
∴S△DOE=S△ADC,所以④错误.
故选:B.
8.解:依题意得
A:(1)当0≤x≤120,yA=30,
(2)当x>120,yA=30+(x﹣120)×[(50﹣30)÷(170﹣120)]=0.4x﹣18;
B:(1)当0≤x<200,yB=50,
当x>200,yB=50+[(70﹣50)÷(250﹣200)](x﹣200)=0.4x﹣30,
所以当x≤120时,A方案比B方案便宜20元,故(1)正确;
当x≥200时,B方案比A方案便宜12元,故(2)正确;
当y=60时,A:60=0.4x﹣18,∴x=195,
B:60=0.4x﹣30,∴x=225,故(3)正确;
当B方案为50元,A方案是40元或者60元时,两种方案通讯费用相差10元,
将yA=40或60代入,得x=145分或195分,故(4)错误;
故选:C.
9.解:在Rt△ABC中,AC=4,∠B=60°,
∴AB=4,BC=8,
由旋转得,AD=AB,
∵∠B=60°,
∴BD=AB=4,
∴CD=BC﹣BD=8﹣4=4,
故选:B.
10.解:①∵抛物线开口向下,
∴a<0.
∵抛物线的对称轴为x=﹣=1,
∴b=﹣2a>0.
当x=0时,y=c>0,
∴abc<0,①错误;
②当x=﹣1时,y<0,
∴a﹣b+c<0,
∴b>a+c,②错误;
③∵抛物线的对称轴为x=1,
∴当x=2时与x=0时,y值相等,
∵当x=0时,y=c>0,
∴4a+2b+c=c>0,③正确;
④∵抛物线与x轴有两个不相同的交点,
∴一元二次方程ax2+bx+c=0,
∴△=b2﹣4ac>0,④正确.
综上可知:成立的结论有2个.
故选:B.
二.填空题(共5小题,满分20分,每小题4分)
11.解:4a3b2﹣6a2b2=2a2b2(2a﹣3).
故答案为:2a2b2(2a﹣3).
12.解:∵关于x的分式方程无解,
∴x=﹣,
原方程去分母得:m(x+1)﹣5=(2x+1)(m﹣3)
解得:x=,m=6时,方程无解.
或=﹣是方程无解,此时m=10.
故答案为6,10.
13.解:设圆锥的母线为a,根据勾股定理得,a=2,
设圆锥的侧面展开图的圆心角度数为n°,
根据题意得2π?1=,解得n=180,
即圆锥的侧面展开图的圆心角度数为180°.
故答案为180°.
14.解:根据规律可得,
当n=2时,CD=AC,tanα1==
当n=3时,CD=AC,tanα2==,
当n=4时,CD=AC,tanα3==,
………………
当n=7时,CD=AC,tanα6==,
故答案为:.
15.解:①根据题意得:a@b=(a+b)2﹣(a﹣b)2
∴(a+b)2﹣(a﹣b)2=0,
整理得:(a+b+a﹣b)(a+b﹣a+b)=0,即4ab=0,
解得:a=0或b=0,正确;
②∵a@(b+c)=(a+b+c)2﹣(a﹣b﹣c)2=4ab+4ac
a@b+a@c=(a+b)2﹣(a﹣b)2+(a+c)2﹣(a﹣c)2=4ab+4ac,
∴a@(b+c)=a@b+a@c,正确;
③∵a@b=a2+5b2,a@b=(a+b)2﹣(a﹣b)2=4ab,
∴a2+5b2=4ab,
∴a2﹣4ab+5b2=0,
∴(a﹣2b)2+b2=0,
∴,
∴,
故错误;
④∵a@b=(a+b)2﹣(a﹣b)2=4ab,
(a﹣b)2≥0,则a2﹣2ab+b2≥0,即a2+b2≥2ab,
∴a2+b2+2ab≥4ab,
∴4ab的最大值是a2+b2+2ab,此时a2+b2+2ab=4ab,
解得a=b,
∴a@b最大时,a=b,故④正确.
故答案为:①②④.
三.解答题(共11小题,满分90分)
16.解:原式=﹣2+2×+2+1,
=﹣2+3+2+1,
=4.
17.解:原式=(+)?
=?
=2(x+2)
=2x+4,
当x=﹣时,
原式=2×(﹣)+4
=﹣1+4
=3.
18.解:(1)∵△=a2﹣4(a﹣2)=a2﹣4a+8=a2﹣4a+4+4=(a﹣2)2+4>0,
∴不论a取何实数,该方程都有两个不相等的实数根;
(2)将x=1代入方程x2+ax+a﹣2=0得,1+a+a﹣2=0,解得a=;
方程为x2+x﹣=0,即2x2+x﹣3=0,
设另一根为x1,则
1?x1=﹣,
解得x1=﹣.
19.解:(1)设温馨提示牌的单价为a元,
4×3a﹣5a=350
解得:a=50,
则3a=150,
答:温馨提示牌、垃圾箱的单价分别为50元和150元;
(2)①由题意可得,
w=50x+150(3000﹣x)=﹣100x+450000,
即购买温馨提示牌和垃圾箱所需费用w(元)与温馨提示牌的个数x的函数关系式是:w=﹣100x+450000;
②由题意得,
,
解得:1000≤x≤1200,
∵x为整数,
∴共有201种可供选择的方案,
∵k=﹣100<0,w随x的增大而减小,
∴当x=1200时,w取得最少值,此时w=330000元,3000﹣x=1800,
答:有201种可供选择的方案,其中购买温馨提示牌1200个,垃圾桶1800个时所需资金最少,最少为330000元.
20.解:CD∥AB,CD=AB,
理由是:∵CE=BF,
∴CE﹣EF=BF﹣EF,
∴CF=BE,
在△AEB和△CFD中,
,
∴△AEB≌△CFD(SAS),
∴CD=AB,∠C=∠B,
∴CD∥AB.
21.解:(1)如图所示:△A′B′C′即为所求;
(2)如图所示:△DPE即为所求.
22.解:(1)10÷20%=50(个),则a=50﹣2﹣6﹣10﹣16﹣4=12,
所抽取参赛学生成绩的中位数是第25个、第26个参赛学生成绩的平均数,
∴所抽取参赛学生成绩的中位数所在的“组别”是D,
故答案为:50,D;
(2)补全频数分布直方图如下:
(3)1200×=480(名),
即估计全校1200名学生中,知识竞赛成绩达到“优秀(90≤x≤100)”的有480名,
故答案为:480;
(4)画树状图如图:
共有12个等可能的结果,恰好选中一名男生和一名女生的结果有8个,
∴恰好选中一名男生和一名女生的概率为=.
23.解:(1)当x<0时,xy=﹣2,而当x>0时,xy=2,
∴m=1,
故答案为:1;补全图象如图所示:
(2)由函数图象的对称性可知,函数的图象关于y轴对称,
从函数的增减性可知,在y轴的左侧(x<0),y随x的增大而增大;在y轴的右侧(x>0),y随x的增大而减小;
故答案为:①函数的图象关于y轴对称,②当x<0时,y随x的增大而增大,当x>0时,y随x的增大而减小;
(3)如图,①由A,B两点关于y轴对称,由题意可得四边形OABC是平行四边形,且S四边形OABC=4S△OAM=4×|k|=2|k|=4,
②同①可知:S四边形OABC=2|k|=4,
③S四边形OABC=2|k|=2k,
故答案为:4,4,2k.
24.解:过D作DH⊥BC于H,过E作EG⊥BC于G.
由已知得,∠BDH=45°,∠CEG=60°,AE=21米,DE=9米.
在Rt△CEG中,CG=AE=21米,tan∠CEG=,
∴EG===7(米).
∴DH=EG=7米.
在Rt△BDH中,∵∠BDH=45°,
∴BH=DH=7米.
∴BC=CG+HG+BH=CG+DE+BH=21+9+7=(30+7)米.
答:大楼BC的高度是(30+7)米.
25.(1)证明:连接OB、OD,如图1所示:
∵AB=DB,AO=DO,BO=BO,
∴△ABO≌△DBO(SSS),
∴∠ABO=∠DBO,
∵OA=OB,∠BDC=∠BAC,
∴∠ABO=∠BAC=∠BDC,
∴∠DBO=∠BDC,
∴OB∥DE,
∵BE⊥DC,
∴BE⊥OB,
∴BE是⊙O的切线;
(2)解:延长BO交AD于点F,如图2所示:
由(1)可知,∠ABO=∠DBO,
∵AB=BD,
∴BF⊥AD,AF=DF=AD=3,
∵∠BAF=∠BCE,∠AFB=∠E=90°,BE=2CE,
∴△ABF∽△CBE,
∴==2,
∴BF=2AF=6,
在Rt△ABF中,由勾股定理得:AB===3,
∴BD=AB=3.
26.解:(1)∵抛物线与x轴交于点A(﹣2,0)、B(3,0),
∴可设抛物线的解析式为:y=a(x+2)(x﹣3)(a≠0),
把C(0,4)代入y=a(x+2)(x﹣3)(a≠0)中,得
4=﹣6a,
∴a=﹣,
∴抛物线的解析式为:y=﹣,
即y=﹣+;
(2)设P点的坐标为(t,),过点P作PM⊥x轴,与BC交于点M,如图1,
设直线BC的解析式为y=kx+b(k≠0),则
,
解得,
∴直线BC的解析式为:y=﹣,
∴M(t,),
∴,
∴=﹣t2+3t,
,
,
∴S四边形ABPC=S△AOC+S△BOC+S△BPC=,
∴当t=时,S四边形ABPC的最大值为,
∴此时P点的坐标为(,);
(3)∵将抛物线向右平移个单位,再向下平移2个单位.记平移后的抛物线为y',
∴y′的解析式为y′=﹣(x﹣)2+(x﹣)+4﹣2,即y′=﹣x2+x+,
∴抛物线y′的对称轴为x=1,
∵抛物线y=﹣+=﹣(x﹣)2+,
∴抛物线y=﹣+的对称轴为直线x=,
把x=代入y′=﹣x2+x+,中,得y′=2,
∴Q点的坐标为(,2),
设E的坐标为(1,n)
①当PE=QE时,则PE2=QE2,
即,
解得,n=,
∴E(1,),
②当PQ=QE时,则PQ2=QE2,
即,
解得,n=2±,
∴E点的坐标为(1,2+)或(1,2﹣);
③当PQ=PE时,则PQ2=PE2,
即,
解得,n=,
∴点E的坐标为(1,)或(1,).
综上,当△PQE是等腰三角形时,点E的坐标为(1,)或(1,2+)或(1,2﹣)或(1,)或(1,).
同课章节目录
