5.1.2《垂线》精品课件(人教版七年级)
文档属性
| 名称 | 5.1.2《垂线》精品课件(人教版七年级) |

|
|
| 格式 | zip | ||
| 文件大小 | 279.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2012-02-26 00:00:00 | ||
图片预览


文档简介
(共17张PPT)
1. 跳水比赛中,入水时水花的大
小直接影响跳水的成绩。那么,
水花的大小是什么原因造成的?
2. 如果用一条直线代表水面,
用另一条直线表示身体,试画出
无水花和水花大的示意图。
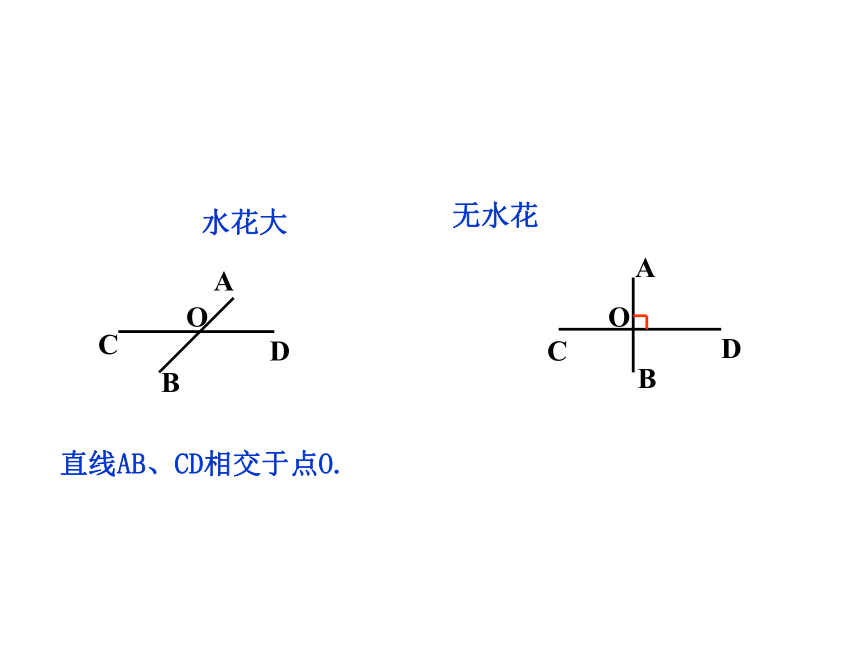
水花大
无水花
C
D
A
B
O
C
A
B
O
直线AB、CD相交于点O.
D
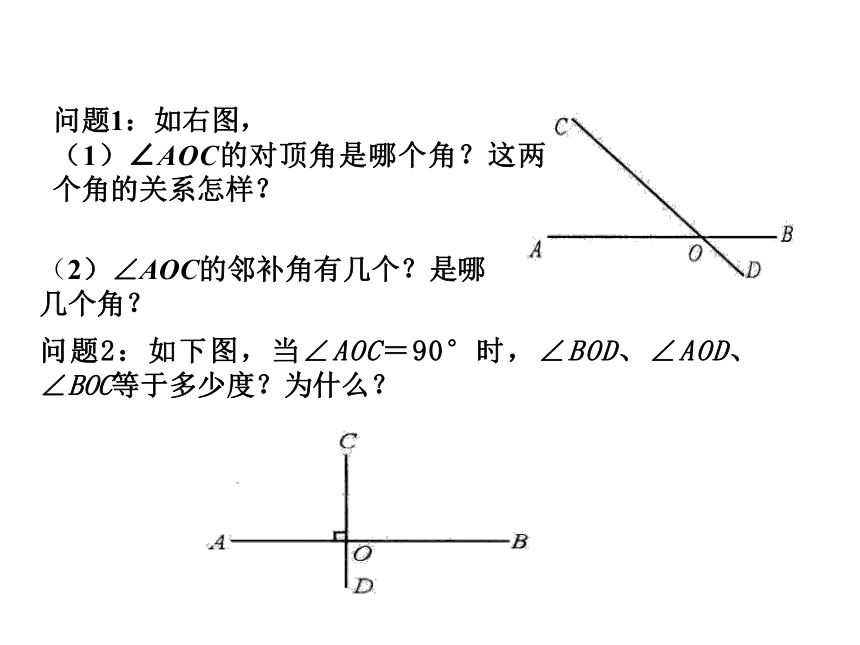
问题1:如右图,
(1)∠AOC的对顶角是哪个角?这两个角的关系怎样?
(2)∠AOC的邻补角有几个?是哪几个角?
问题2:如下图,当∠AOC=90°时,∠BOD、∠AOD、∠BOC等于多少度?为什么?
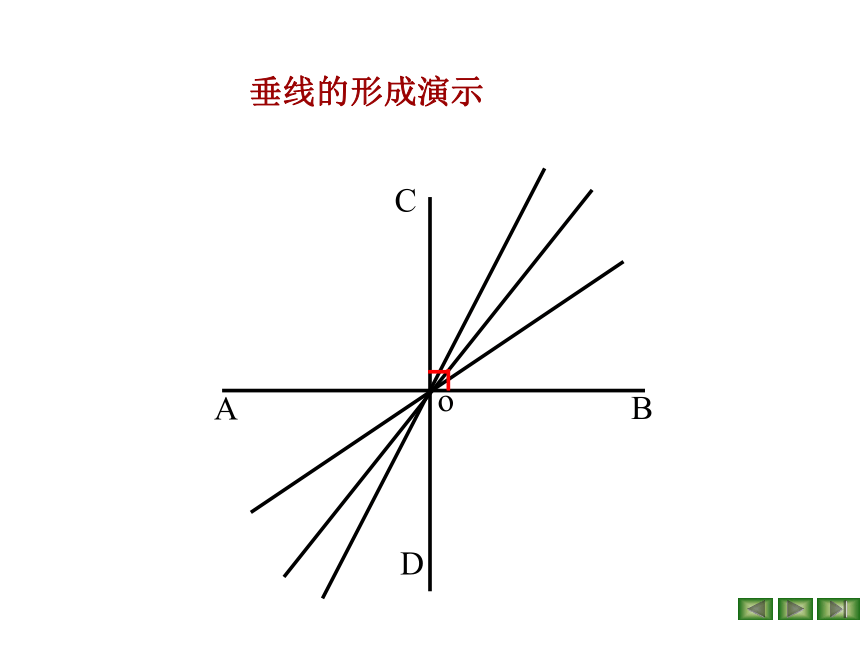
垂线的形成演示
o
A
B
C
D
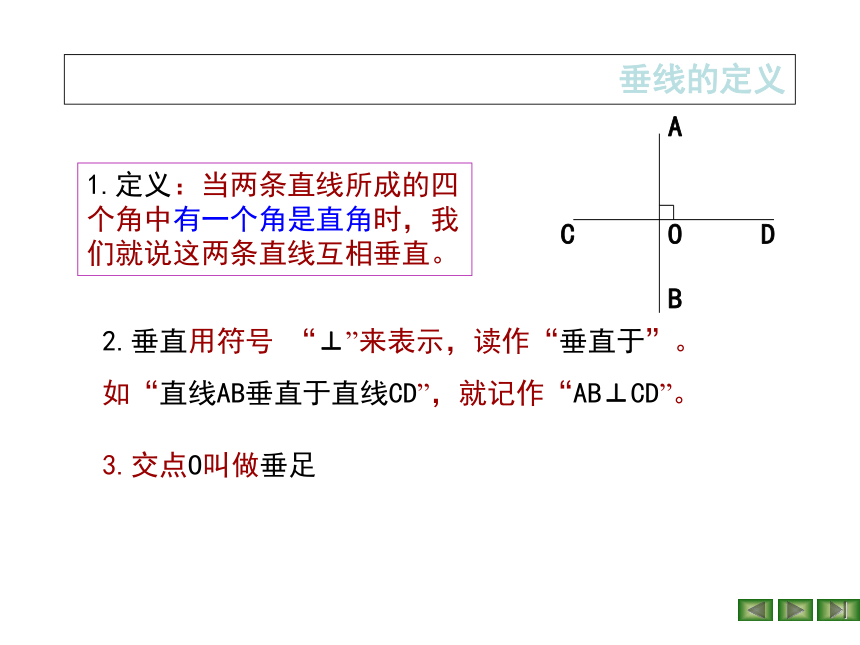
1.定义:当两条直线所成的四个角中有一个角是直角时,我们就说这两条直线互相垂直。
2.垂直用符号 “⊥”来表示,读作“垂直于”。
如“直线AB垂直于直线CD”,就记作“AB⊥CD”。
O
A
B
C
D
3.交点O叫做垂足
F
E
M
N
O
记作: MN⊥EF , 垂足为O.
或者MN⊥EF于F
A
B
O
E
记作: AB⊥OE垂足为O.
或者AB⊥OE于O
1、∵AB⊥CD(已知)
∴∠1=90°(垂线的定义)
2、∵∠1=90°(已知)
∴AB⊥CD(垂线的定义)
A
B
C
D
1
A
B
C
D
1
画一条直线的垂线,这样的垂线能画多少条?
过直线上一点作已知直线的垂线,这样的垂线能画多少条?
过直线外一点作已知直线的垂线,这样的垂线能画多少条?
(无数条)
(一条)
(一条)
画垂线的基本方法:
一贴:
二靠:
三画:
三角尺的一条直角边贴住已知直线
另一条直角边靠住已知点
按要求画垂线
根据以上的结果,你能得出什么结论?
垂线的第一性质:
过一点有且只有一条直线与已知直线垂直。
(1)“有且只有”中,“有”指存在,“只有”指唯一性。
(2)“过一点”中的点,可以在已知直线上,也可以在已知直线外。
注意:
合作学习
答:垂线段PO最短.
连接直线外一点与直线上各点的所有线段中,垂线段最短。
也可简单地说成:垂线段最短。
直线外一点到这条直线的垂线段的长度,叫做点到直线的距离。
问:图中点P到直线 l 的距离是什么?
在直线l上任意选取点A1,A2,A3,……,B1,B2,B3,……,分别与直线l外一点P连接,所成的线段PA1、PA2、PA3、……,PB1、PB2、PB3、……中,哪一条线段最短?
l
P
A1
A2
O
B3
B2
B1
A3
点到直线的距离的概念
直线外一点到已知直线的垂线段的长度就叫做点到直线的距离。
A
P
B
Q
如图,点P到直线AB的距离就是垂线段PQ的长度
解:
∵∠1=35°,∠2=55°(已知)
垂直
∴ ∠AOE=180°-∠1-∠2
= 180°-35°-55°
=90°
∴OE⊥AB (垂直的定义)
C
D
A
B
O
E
1
2
例1、如图,已知直线AB、CD都经过O点,OE为射线,若∠1=35° ∠2=55°,则OE与AB的位置关系是 。
例2:如图 ,已知AB. CD相交于O, OE⊥CD
于O,∠AOC=36°,则∠BOE= 。
(A)36° (B) 64°
(C)144° (D) 54°
A
B
O
C
D
E
D
1. 理解了垂线的概念,会用三角尺、量角器过一点画一条直线的垂线;
2. 理解了点到直线的距离的概念,并会度量点到直线的距离。
3. 掌握了垂线的两个性质
学到了什么
1. 跳水比赛中,入水时水花的大
小直接影响跳水的成绩。那么,
水花的大小是什么原因造成的?
2. 如果用一条直线代表水面,
用另一条直线表示身体,试画出
无水花和水花大的示意图。
水花大
无水花
C
D
A
B
O
C
A
B
O
直线AB、CD相交于点O.
D
问题1:如右图,
(1)∠AOC的对顶角是哪个角?这两个角的关系怎样?
(2)∠AOC的邻补角有几个?是哪几个角?
问题2:如下图,当∠AOC=90°时,∠BOD、∠AOD、∠BOC等于多少度?为什么?
垂线的形成演示
o
A
B
C
D
1.定义:当两条直线所成的四个角中有一个角是直角时,我们就说这两条直线互相垂直。
2.垂直用符号 “⊥”来表示,读作“垂直于”。
如“直线AB垂直于直线CD”,就记作“AB⊥CD”。
O
A
B
C
D
3.交点O叫做垂足
F
E
M
N
O
记作: MN⊥EF , 垂足为O.
或者MN⊥EF于F
A
B
O
E
记作: AB⊥OE垂足为O.
或者AB⊥OE于O
1、∵AB⊥CD(已知)
∴∠1=90°(垂线的定义)
2、∵∠1=90°(已知)
∴AB⊥CD(垂线的定义)
A
B
C
D
1
A
B
C
D
1
画一条直线的垂线,这样的垂线能画多少条?
过直线上一点作已知直线的垂线,这样的垂线能画多少条?
过直线外一点作已知直线的垂线,这样的垂线能画多少条?
(无数条)
(一条)
(一条)
画垂线的基本方法:
一贴:
二靠:
三画:
三角尺的一条直角边贴住已知直线
另一条直角边靠住已知点
按要求画垂线
根据以上的结果,你能得出什么结论?
垂线的第一性质:
过一点有且只有一条直线与已知直线垂直。
(1)“有且只有”中,“有”指存在,“只有”指唯一性。
(2)“过一点”中的点,可以在已知直线上,也可以在已知直线外。
注意:
合作学习
答:垂线段PO最短.
连接直线外一点与直线上各点的所有线段中,垂线段最短。
也可简单地说成:垂线段最短。
直线外一点到这条直线的垂线段的长度,叫做点到直线的距离。
问:图中点P到直线 l 的距离是什么?
在直线l上任意选取点A1,A2,A3,……,B1,B2,B3,……,分别与直线l外一点P连接,所成的线段PA1、PA2、PA3、……,PB1、PB2、PB3、……中,哪一条线段最短?
l
P
A1
A2
O
B3
B2
B1
A3
点到直线的距离的概念
直线外一点到已知直线的垂线段的长度就叫做点到直线的距离。
A
P
B
Q
如图,点P到直线AB的距离就是垂线段PQ的长度
解:
∵∠1=35°,∠2=55°(已知)
垂直
∴ ∠AOE=180°-∠1-∠2
= 180°-35°-55°
=90°
∴OE⊥AB (垂直的定义)
C
D
A
B
O
E
1
2
例1、如图,已知直线AB、CD都经过O点,OE为射线,若∠1=35° ∠2=55°,则OE与AB的位置关系是 。
例2:如图 ,已知AB. CD相交于O, OE⊥CD
于O,∠AOC=36°,则∠BOE= 。
(A)36° (B) 64°
(C)144° (D) 54°
A
B
O
C
D
E
D
1. 理解了垂线的概念,会用三角尺、量角器过一点画一条直线的垂线;
2. 理解了点到直线的距离的概念,并会度量点到直线的距离。
3. 掌握了垂线的两个性质
学到了什么
