8.3简单几何体的表面积与体积-【新教材】2020-2021学年人教A版(2019)高中数学必修第二册专题训练(Word版含答案)
文档属性
| 名称 | 8.3简单几何体的表面积与体积-【新教材】2020-2021学年人教A版(2019)高中数学必修第二册专题训练(Word版含答案) |
|
|
| 格式 | docx | ||
| 文件大小 | 143.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-04-19 00:00:00 | ||
图片预览


文档简介
高一数学人教版(2019)必修第二册
【8.3简单几何体的表面积与体积专题训练】
【基础巩固】
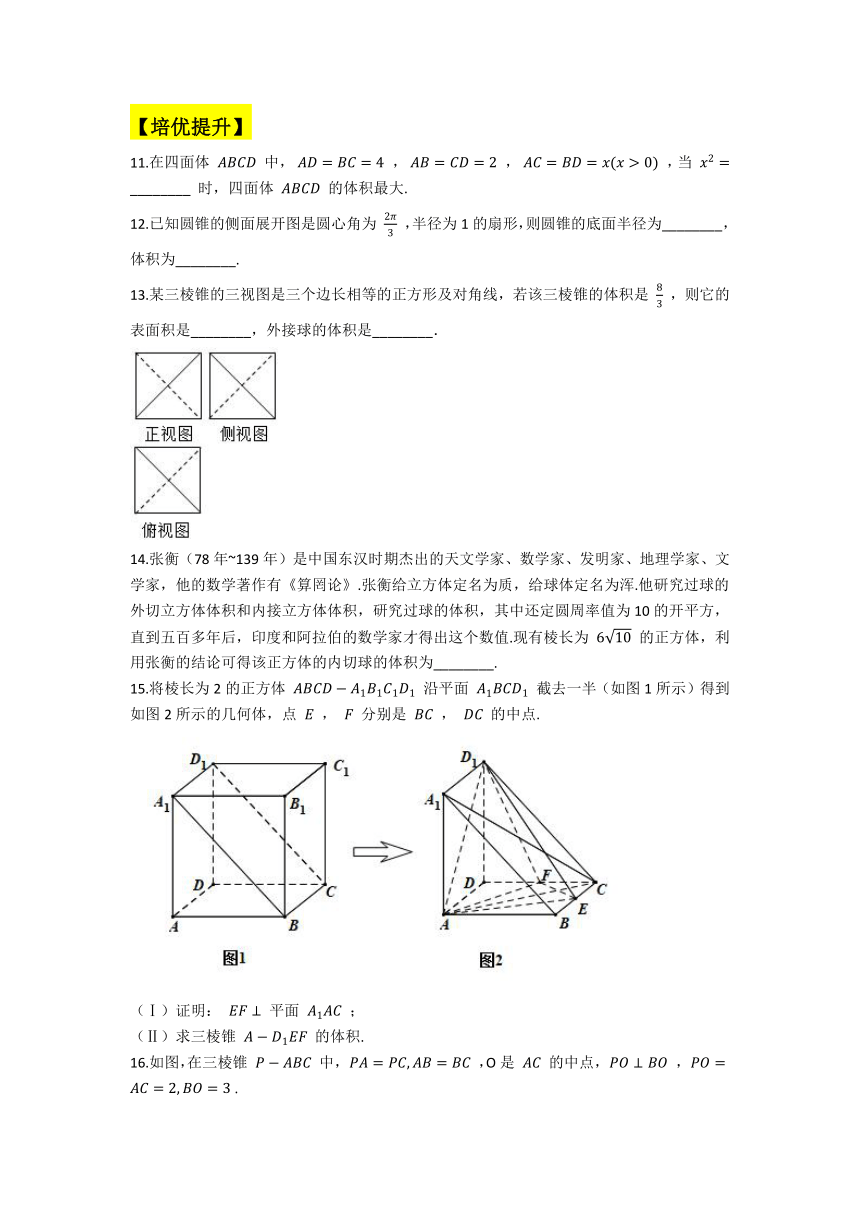
1.如图,在三棱锥 D?ABC 中, AD⊥BC,BC=1,AD=1 .且 AB+BD=AC+CD=2 ,则四面体 ABCD 的体积的最大值为(??? )
A.?14???????????????????????????????????????B.?212???????????????????????????????????????C.?36???????????????????????????????????????D.?524
2.经过圆锥的轴的截面是面积为2的等腰直角三角形,则圆锥的侧面积是(??? )
A.?42π?????????????????????????????????????B.?4π?????????????????????????????????????C.?22π?????????????????????????????????????D.?2π
3.一个体积为 243 的正三棱柱(底面为正三角形,且侧棱垂直于底面)的三视图如图所示,则侧视图的面积为(??? )
A.?63???????????????????????????????????????B.?8???????????????????????????????????????C.?123???????????????????????????????????????D.?12
4.已知三棱锥的三条侧棱两两相互垂直,且三个侧面的面积分别为4,6,12,则这个三棱锥的外接球的表面积为(??? ).
A.?56π???????????????????????????????B.?224π???????????????????????????????C.?5614π3???????????????????????????????D.?44814π3
5.将周长为4的矩形 ABCD 绕 AB 旋转一周所得圆柱体积最大时, AB 长为(?? )
A.?43??????????????????????????????????????????B.?23??????????????????????????????????????????C.?13??????????????????????????????????????????D.?1
6.已知正方体 ABCD?A1B1C1D1 的棱长为2, E 为棱 AA1 的中点,截面 CD1E 交棱 AB 于点 F ,则四面体 CDFD1 的外接球表面积为(??? )
A.?39π4?????????????????????????????????????B.?41π4?????????????????????????????????????C.?12π?????????????????????????????????????D.?43π4
7.如图是某四面体 ABCD 水平放置时的三视图,图中网格纸的小正方形的边长为1,则四面体 ABCD 外接球的体积为(??? )
A.?500π3??????????????????????????????????B.?100π3??????????????????????????????????C.?125π6??????????????????????????????????D.?20π
8.现有一个三棱锥形状的工艺品 P?ABC ,点 P 在底面 ABC 的投影为 Q ,满足 S△QABS△PAB=S△QACS△PAC=S△QBCS△PBC=12 , QA2+QB2+QC2AB2+BC2+CA2=13 , S△ABC=93 ,若要将此工艺品放入一个球形容器(不计此球形容器的厚度)中,则该球形容器的表面积的最小值为(??? )
A.?42π?????????????????????????????????????B.?44π?????????????????????????????????????C.?48π?????????????????????????????????????D.?49π
9.用与球心距离为1的平面去截面面积为 π ,则球的体积为(?? )
A.?32π3????????????????????????????????????B.?8π3????????????????????????????????????C.?82π????????????????????????????????????D.?82π3
10.已知三棱锥 A?BCD 的四个顶点A、B、C、D都在半径为 3 的球O的表面上,AC⊥平面 BCD ,BD=3,BC=2, CD=5 ,则该三棱锥的体积为(??? )
A.?153???????????????????????????????????B.?2153???????????????????????????????????C.?156???????????????????????????????????D.?15
【培优提升】
11.在四面体 ABCD 中, AD=BC=4 , AB=CD=2 , AC=BD=x(x>0) ,当 x2= ________ 时,四面体 ABCD 的体积最大.
12.已知圆锥的侧面展开图是圆心角为 2π3 ,半径为1的扇形,则圆锥的底面半径为________,体积为________.
13.某三棱锥的三视图是三个边长相等的正方形及对角线,若该三棱锥的体积是 83 ,则它的表面积是________,外接球的体积是________.
14.张衡(78年~139年)是中国东汉时期杰出的天文学家、数学家、发明家、地理学家、文学家,他的数学著作有《算罔论》.张衡给立方体定名为质,给球体定名为浑.他研究过球的外切立方体体积和内接立方体体积,研究过球的体积,其中还定圆周率值为10的开平方,直到五百多年后,印度和阿拉伯的数学家才得出这个数值.现有棱长为 610 的正方体,利用张衡的结论可得该正方体的内切球的体积为________.
15.将棱长为2的正方体 ABCD?A1B1C1D1 沿平面 A1BCD1 截去一半(如图1所示)得到如图2所示的几何体,点 E , F 分别是 BC , DC 的中点.
(Ⅰ)证明: EF⊥ 平面 A1AC ;
(Ⅱ)求三棱锥 A?D1EF 的体积.
16.如图,在三棱锥 P?ABC 中, PA=PC,AB=BC ,O是 AC 的中点, PO⊥BO , PO=AC=2,BO=3 .
(1)证明: AC⊥PB ;
(2)求三棱锥 A?PBC 的体积.
17.如图,在三棱柱 ABC?A1B1C1 中, B1C⊥ 平面 ABC ,侧面 ABB1A1 为矩形, AB=1,AA1=AC=2 .
(1)证明:平面 ABB1A1⊥ 平面 BB1C ;
(2)求四棱锥 C?ABB1A1 的体积.
18.如图,四棱锥 S?ABCD 的底面是正方形, SD⊥ 平面 ABCD , SD=2 , AD=2 ,点 E 是线段 SD 上的点,且 DE=a(0(1)求证:对任意的 0(2)当 a=1 时,点 M 是 SC 上的点,且 SM=2MC ,求三棱锥 E?BCM 的体积.
【参考答案】
1.【答案】 B
2.【答案】 C
3.【答案】 C
4.【答案】 A
5.【答案】 B
6.【答案】 B
7.【答案】 C
8.【答案】 D
9.【答案】 D
10.【答案】 A
11.【答案】 20+8133
12.【答案】 13;2281π
13.【答案】 83;43π
14.【答案】 3600
15.【答案】 解:(Ⅰ)如图所示:
连接 BD ,易知 BD⊥AC ,
因为 A1A⊥ 平面 ABCD , BD? 平面 ABCD ,
所以 A1A⊥BD ,又 A1A∩AC=A ,
所以 BD⊥ 平面 A1AC .
在 △CBD 中,点 E , F 分别是 BC , DC 的中点,
所以 BD//EF .
所以 EF⊥ 平面 A1AC .
(Ⅱ)∵ D1D⊥ 平面 ABCD ,
∴ D1D 是三棱锥 D1?AEF 在平面 AEF 上的高,且 D1D=2 .
∵点 E , F 分别是 BC , DC 的中点,
∴ DF=CF=CE=BE=1 .
∴ S△AEF=22?12?AD?DF?12?CF?CE?12?AB?BE=32 .
∴ VA?D1EF=VD1?AEF=13?S△AEF?D1D=13×32×2=1
16.【答案】 (1)证明: ∵ PA=PC,AB=BC ,O是 AC 的中点,
∴PO⊥AC,BO⊥AC ,
∵PO∩BO=O , ∴AC⊥ 平面 POB ,
∴ AC⊥PB
(2)解: ∵PO⊥AC,PO⊥BO , AC∩BO=O ,
∴PO⊥ 平面 ABC ,即 PO 是三棱锥的高,
∴VA?PBC=13S△ABC?PO=13×12×2×3×2=2
17.【答案】 (1)证明:∵ B1C⊥ 平面 ABC , AB? 平面 ABC ,∴ B1C⊥AB ,
又四边形 ABB1A1 为矩形,∴ AB⊥B1B .
又∵ B1B∩B1C=B1 , B1B? 平面 BB1C , B1C? 平面 BB1C ,∴ AB⊥ 平面 BB1C ,
又 AB? 平面 ABB1A1 ,∴平面 ABB1A1⊥ 平面 BB1C
(2)解:由(1)知 AB⊥ 平面 BB1C ,∴ AB⊥BC ,
则 BC=AC2?AB2=3 ,从而 B1C=22?(3)2=1 ,
在 △BB1C 中,过点 C 作 CD⊥BB1 于点 D ,
由于平面 ABB1A1⊥ 平面 BB1C ,平面 ABB1A1∩ 平面 BB1C=BB1 ,
∴ CD⊥ 平面 ABB1A1 ,
由 S△B1BC=12B1C?BC=12BB1?CD 可得 CD=32 ,
∴四棱锥 C?ABB1A1 的体积为 V=13S?ABB1A1?CD=13×1×2×32=33
18.【答案】 (1)证明:连接 BD ,由 ABCD 是正方形,
则 AC⊥BD ,
又 SD⊥ 平面 ABCD .
则 AC⊥SD , SD∩BD=D ,
所以 AC⊥ 面 SBD ,又 BE? 面 SBD ,
所以 AC⊥BE .
(2)解:由题 VE?BCM=VB?ECM=13SΔECM?? ,
易知 BC⊥ 面 SDC ,所以 ?=BC=2 ,
SΔECM=16SΔSDC=16×12×2×2=26 ,
则 VE?BCM=13SΔECM??=13×26×2=19
【8.3简单几何体的表面积与体积专题训练】
【基础巩固】
1.如图,在三棱锥 D?ABC 中, AD⊥BC,BC=1,AD=1 .且 AB+BD=AC+CD=2 ,则四面体 ABCD 的体积的最大值为(??? )
A.?14???????????????????????????????????????B.?212???????????????????????????????????????C.?36???????????????????????????????????????D.?524
2.经过圆锥的轴的截面是面积为2的等腰直角三角形,则圆锥的侧面积是(??? )
A.?42π?????????????????????????????????????B.?4π?????????????????????????????????????C.?22π?????????????????????????????????????D.?2π
3.一个体积为 243 的正三棱柱(底面为正三角形,且侧棱垂直于底面)的三视图如图所示,则侧视图的面积为(??? )
A.?63???????????????????????????????????????B.?8???????????????????????????????????????C.?123???????????????????????????????????????D.?12
4.已知三棱锥的三条侧棱两两相互垂直,且三个侧面的面积分别为4,6,12,则这个三棱锥的外接球的表面积为(??? ).
A.?56π???????????????????????????????B.?224π???????????????????????????????C.?5614π3???????????????????????????????D.?44814π3
5.将周长为4的矩形 ABCD 绕 AB 旋转一周所得圆柱体积最大时, AB 长为(?? )
A.?43??????????????????????????????????????????B.?23??????????????????????????????????????????C.?13??????????????????????????????????????????D.?1
6.已知正方体 ABCD?A1B1C1D1 的棱长为2, E 为棱 AA1 的中点,截面 CD1E 交棱 AB 于点 F ,则四面体 CDFD1 的外接球表面积为(??? )
A.?39π4?????????????????????????????????????B.?41π4?????????????????????????????????????C.?12π?????????????????????????????????????D.?43π4
7.如图是某四面体 ABCD 水平放置时的三视图,图中网格纸的小正方形的边长为1,则四面体 ABCD 外接球的体积为(??? )
A.?500π3??????????????????????????????????B.?100π3??????????????????????????????????C.?125π6??????????????????????????????????D.?20π
8.现有一个三棱锥形状的工艺品 P?ABC ,点 P 在底面 ABC 的投影为 Q ,满足 S△QABS△PAB=S△QACS△PAC=S△QBCS△PBC=12 , QA2+QB2+QC2AB2+BC2+CA2=13 , S△ABC=93 ,若要将此工艺品放入一个球形容器(不计此球形容器的厚度)中,则该球形容器的表面积的最小值为(??? )
A.?42π?????????????????????????????????????B.?44π?????????????????????????????????????C.?48π?????????????????????????????????????D.?49π
9.用与球心距离为1的平面去截面面积为 π ,则球的体积为(?? )
A.?32π3????????????????????????????????????B.?8π3????????????????????????????????????C.?82π????????????????????????????????????D.?82π3
10.已知三棱锥 A?BCD 的四个顶点A、B、C、D都在半径为 3 的球O的表面上,AC⊥平面 BCD ,BD=3,BC=2, CD=5 ,则该三棱锥的体积为(??? )
A.?153???????????????????????????????????B.?2153???????????????????????????????????C.?156???????????????????????????????????D.?15
【培优提升】
11.在四面体 ABCD 中, AD=BC=4 , AB=CD=2 , AC=BD=x(x>0) ,当 x2= ________ 时,四面体 ABCD 的体积最大.
12.已知圆锥的侧面展开图是圆心角为 2π3 ,半径为1的扇形,则圆锥的底面半径为________,体积为________.
13.某三棱锥的三视图是三个边长相等的正方形及对角线,若该三棱锥的体积是 83 ,则它的表面积是________,外接球的体积是________.
14.张衡(78年~139年)是中国东汉时期杰出的天文学家、数学家、发明家、地理学家、文学家,他的数学著作有《算罔论》.张衡给立方体定名为质,给球体定名为浑.他研究过球的外切立方体体积和内接立方体体积,研究过球的体积,其中还定圆周率值为10的开平方,直到五百多年后,印度和阿拉伯的数学家才得出这个数值.现有棱长为 610 的正方体,利用张衡的结论可得该正方体的内切球的体积为________.
15.将棱长为2的正方体 ABCD?A1B1C1D1 沿平面 A1BCD1 截去一半(如图1所示)得到如图2所示的几何体,点 E , F 分别是 BC , DC 的中点.
(Ⅰ)证明: EF⊥ 平面 A1AC ;
(Ⅱ)求三棱锥 A?D1EF 的体积.
16.如图,在三棱锥 P?ABC 中, PA=PC,AB=BC ,O是 AC 的中点, PO⊥BO , PO=AC=2,BO=3 .
(1)证明: AC⊥PB ;
(2)求三棱锥 A?PBC 的体积.
17.如图,在三棱柱 ABC?A1B1C1 中, B1C⊥ 平面 ABC ,侧面 ABB1A1 为矩形, AB=1,AA1=AC=2 .
(1)证明:平面 ABB1A1⊥ 平面 BB1C ;
(2)求四棱锥 C?ABB1A1 的体积.
18.如图,四棱锥 S?ABCD 的底面是正方形, SD⊥ 平面 ABCD , SD=2 , AD=2 ,点 E 是线段 SD 上的点,且 DE=a(0
【参考答案】
1.【答案】 B
2.【答案】 C
3.【答案】 C
4.【答案】 A
5.【答案】 B
6.【答案】 B
7.【答案】 C
8.【答案】 D
9.【答案】 D
10.【答案】 A
11.【答案】 20+8133
12.【答案】 13;2281π
13.【答案】 83;43π
14.【答案】 3600
15.【答案】 解:(Ⅰ)如图所示:
连接 BD ,易知 BD⊥AC ,
因为 A1A⊥ 平面 ABCD , BD? 平面 ABCD ,
所以 A1A⊥BD ,又 A1A∩AC=A ,
所以 BD⊥ 平面 A1AC .
在 △CBD 中,点 E , F 分别是 BC , DC 的中点,
所以 BD//EF .
所以 EF⊥ 平面 A1AC .
(Ⅱ)∵ D1D⊥ 平面 ABCD ,
∴ D1D 是三棱锥 D1?AEF 在平面 AEF 上的高,且 D1D=2 .
∵点 E , F 分别是 BC , DC 的中点,
∴ DF=CF=CE=BE=1 .
∴ S△AEF=22?12?AD?DF?12?CF?CE?12?AB?BE=32 .
∴ VA?D1EF=VD1?AEF=13?S△AEF?D1D=13×32×2=1
16.【答案】 (1)证明: ∵ PA=PC,AB=BC ,O是 AC 的中点,
∴PO⊥AC,BO⊥AC ,
∵PO∩BO=O , ∴AC⊥ 平面 POB ,
∴ AC⊥PB
(2)解: ∵PO⊥AC,PO⊥BO , AC∩BO=O ,
∴PO⊥ 平面 ABC ,即 PO 是三棱锥的高,
∴VA?PBC=13S△ABC?PO=13×12×2×3×2=2
17.【答案】 (1)证明:∵ B1C⊥ 平面 ABC , AB? 平面 ABC ,∴ B1C⊥AB ,
又四边形 ABB1A1 为矩形,∴ AB⊥B1B .
又∵ B1B∩B1C=B1 , B1B? 平面 BB1C , B1C? 平面 BB1C ,∴ AB⊥ 平面 BB1C ,
又 AB? 平面 ABB1A1 ,∴平面 ABB1A1⊥ 平面 BB1C
(2)解:由(1)知 AB⊥ 平面 BB1C ,∴ AB⊥BC ,
则 BC=AC2?AB2=3 ,从而 B1C=22?(3)2=1 ,
在 △BB1C 中,过点 C 作 CD⊥BB1 于点 D ,
由于平面 ABB1A1⊥ 平面 BB1C ,平面 ABB1A1∩ 平面 BB1C=BB1 ,
∴ CD⊥ 平面 ABB1A1 ,
由 S△B1BC=12B1C?BC=12BB1?CD 可得 CD=32 ,
∴四棱锥 C?ABB1A1 的体积为 V=13S?ABB1A1?CD=13×1×2×32=33
18.【答案】 (1)证明:连接 BD ,由 ABCD 是正方形,
则 AC⊥BD ,
又 SD⊥ 平面 ABCD .
则 AC⊥SD , SD∩BD=D ,
所以 AC⊥ 面 SBD ,又 BE? 面 SBD ,
所以 AC⊥BE .
(2)解:由题 VE?BCM=VB?ECM=13SΔECM?? ,
易知 BC⊥ 面 SDC ,所以 ?=BC=2 ,
SΔECM=16SΔSDC=16×12×2×2=26 ,
则 VE?BCM=13SΔECM??=13×26×2=19
同课章节目录
- 第六章 平面向量及其应用
- 6.1 平面向量的概念
- 6.2 平面向量的运算
- 6.3 平面向量基本定理及坐标表示
- 6.4 平面向量的应用
- 第七章 复数
- 7.1 复数的概念
- 7.2 复数的四则运算
- 7.3 * 复数的三角表示
- 第八章 立体几何初步
- 8.1 基本立体图形
- 8.2 立体图形的直观图
- 8.3 简单几何体的表面积与体积
- 8.4 空间点、直线、平面之间的位置关系
- 8.5 空间直线、平面的平行
- 8.6 空间直线、平面的垂直
- 第九章 统计
- 9.1 随机抽样
- 9.2 用样本估计总体
- 9.3 统计分析案例 公司员工
- 第十章 概率
- 10.1 随机事件与概率
- 10.2 事件的相互独立性
- 10.3 频率与概率
