8.4空间点、直线、平面之间的位置关系-【新教材】2020-2021学年人教A版(2019)高中数学必修第二册专题训练(Word版含答案)
文档属性
| 名称 | 8.4空间点、直线、平面之间的位置关系-【新教材】2020-2021学年人教A版(2019)高中数学必修第二册专题训练(Word版含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 89.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-04-19 00:00:00 | ||
图片预览


文档简介
高一数学人教版(2019)必修第二册
【专题训练】
【基础巩固】
1.如果空间四点A,B,C,D不共面,那么下列判断中正确的是(??? )
A.?A,B,C,D四点中必有三点共线
B.?直线 AB 与 CD 相交
C.?A,B,C,D四点中不存在三点共线
D.?直线 AB 与 CD 平行
2.设l为一条直线, α,β 是两个不同的平面,下列命题正确的是(??? )
A.?若 α⊥β,l//α ,则 l⊥β
B.?若 l//α , l//β ,则 α//β
C.?若 l⊥α,l⊥β ,则 α//β
D.?若 l⊥α,l//β ,则 α//β
3.在空间直角坐标系中,若直线l的方向向量为 a=(1,?2,1) ,平面 α 的法向量为 n=(2,3,4) ,则(??? )
A.?l//α?????????????????????????????B.?l⊥α?????????????????????????????C.?l?α 或 l//α?????????????????????????????D.?l与 α 斜交
4.已知m,n为两条不同的直线, α//β 是两个不同的平面,下列命题为真命题的是(??? )
A.?m⊥n,m//α?n⊥α??????????????????????????????????????B.?n//β,β⊥α?n⊥α
C.?m//n,m⊥β?n⊥β??????????????????????????????????????D.?m//α,n?α?m//n
5.已知m,n为两条不同的直线, α,β 是两个不同的平面,给出下列4个命题:
① m⊥n,m//α?n⊥α ;② n//β,β⊥α?n⊥α ;③ m//n,m⊥β?n⊥β ;④ m//α,n⊥α?m⊥n .其中所有真命题的序号是(??? )
A.?①③?????????????????????????????????????B.?②④?????????????????????????????????????C.?②③?????????????????????????????????????D.?③④
6.已知P,Q是不同的点,l,m,n是不同的直线, α , β 是不同的平面,则下列数学符号表示的命题中,不是公理的是(??? )
A.?P∈l , Q∈l , P∈α , Q∈α?l?α
B.?P∈α , P∈β? 存在唯一直线l, α∩β=l ,且 P∈l
C.?l//m , m//n?l//n
D.?m⊥α , n⊥α?m//n
7.设 α , β 是两个不同的平面, l 是一条直线,以下结论正确的是(??? )
A.?若 l⊥α , α//β ,则 l⊥β
B.?若 l//α , l//β ,则 α//β
C.?若 l⊥α , α⊥β ,则 l?β
D.?若 l//α , α⊥β ,则 l⊥β
8.已知正方体 ABCD?A1B1C1D1 的棱长为3,E,F,G分别为棱 AA1 , AB , CC1 上的点,其中 AE=1 , AF=2 , CG=32 ,平面 α 经过点E,F,G,则 α 截此正方体所得的截面为(??? )
A.?三角形????????????????????????????????B.?四边形????????????????????????????????C.?五边形????????????????????????????????D.?六边形
9.下列命题中正确的是(??? )
A.?三点确定一个平面
B.?垂直于同一直线的两条直线平行
C.?若直线 l 与平面 α 上的无数条直线都垂直,则直线 l⊥α
D.?若 a、b、c 是三条直线, a//b 且与 c 都相交,则直线 a、b、c 共面.
10.已知 a,b 是两条直线, α,β 是两个平面,则 a⊥b 的一个充分条件是(??? )
A.?a⊥α , b//β , α⊥β???????????????????????????????????B.?a⊥α , b⊥β , α//β
C.?a?α , b⊥β , α//β???????????????????????????????????D.?a?α , b//β , α⊥β
【培优提升】
11.已知 α,β 是两个不同的平面, l,m 是两条不同的直线, l⊥α,m?β .给出下列命题:
① α//β?l⊥m ;② α⊥β?l//m ;③ m//α?l⊥β ;④ l⊥β?m//α .
其中正确的命题是________.
12.如图所示,在直角梯形 ABCD 中, BC⊥DC,AE⊥DC,M,N 分别是 AD,BE 的中点,将三角形 ADE 沿 AE 折起,下列说法正确的是________(填上所有正确的序号).
①不论 D 折至何位置(不在平面 ABC 内)都有 MN∥ 平面 DEC ;
②不论 D 折至何位置都有 MN⊥AE ;
③不论 D 折至何位置(不在平面 ABC 内)都有 MN∥AB .
13.下列说法中正确的有________个.
①空间中三条直线交于一点,则这三条直线共面;
②一个平行四边形确定一个平面;
③若一个角的两边分别平行于另一个角的两边,则这两个角相等;
④已知两个不同的平面 α 和 β ,若 A∈α , A∈β ,且 α∩β=l ,则点A在直线 l 上.
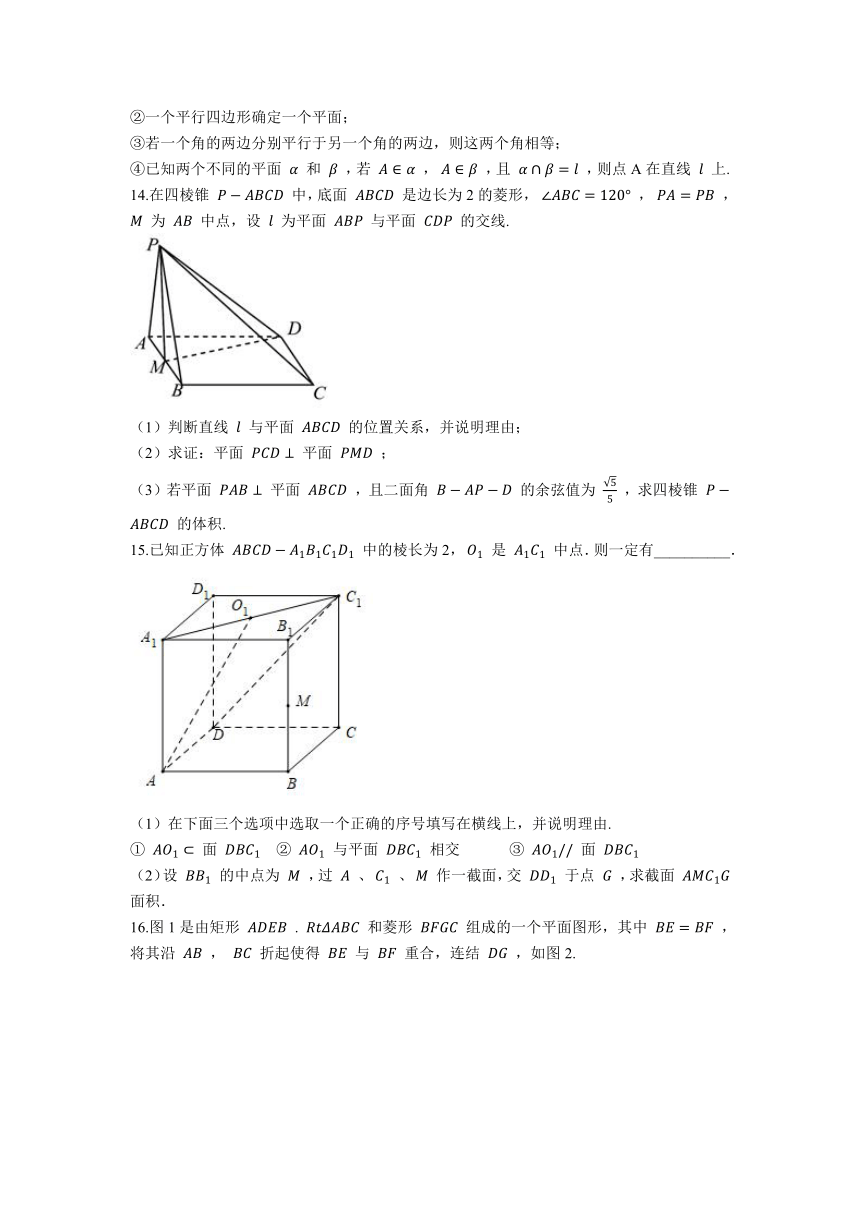
14.在四棱锥 P?ABCD 中,底面 ABCD 是边长为2的菱形, ∠ABC=120° , PA=PB , M 为 AB 中点,设 l 为平面 ABP 与平面 CDP 的交线.
(1)判断直线 l 与平面 ABCD 的位置关系,并说明理由;
(2)求证:平面 PCD⊥ 平面 PMD ;
(3)若平面 PAB⊥ 平面 ABCD ,且二面角 B?AP?D 的余弦值为 55 ,求四棱锥 P?ABCD 的体积.
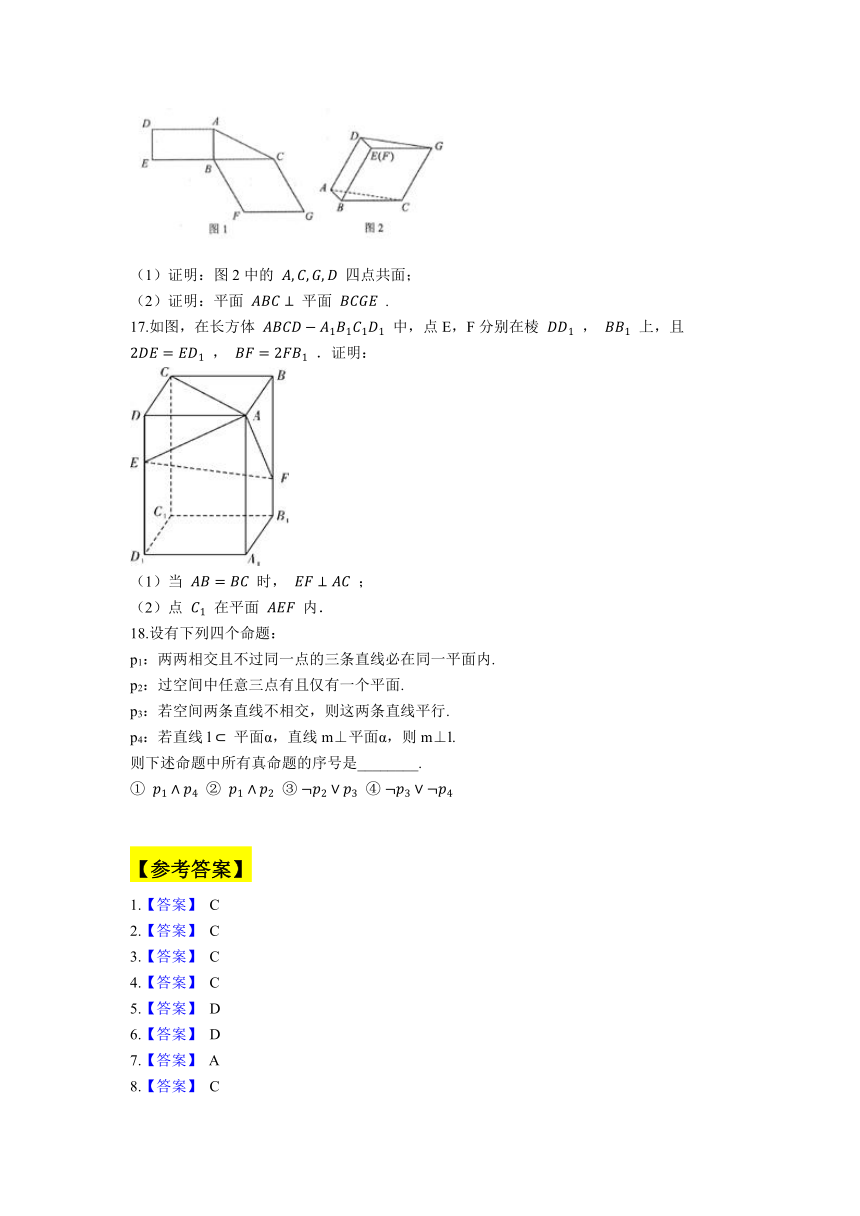
15.已知正方体 ABCD?A1B1C1D1 中的棱长为2, O1 是 A1C1 中点.则一定有__________.
(1)在下面三个选项中选取一个正确的序号填写在横线上,并说明理由.
① AO1? 面 DBC1 ② AO1 与平面 DBC1 相交??????????? ③ AO1// 面 DBC1
(2)设 BB1 的中点为 M ,过 A 、 C1 、 M 作一截面,交 DD1 于点 G ,求截面 AMC1G 面积.
16.图1是由矩形 ADEB . RtΔABC 和菱形 BFGC 组成的一个平面图形,其中 BE=BF ,将其沿 AB , BC 折起使得 BE 与 BF 重合,连结 DG ,如图2.
(1)证明:图2中的 A,C,G,D 四点共面;
(2)证明:平面 ABC⊥ 平面 BCGE .
17.如图,在长方体 ABCD?A1B1C1D1 中,点E,F分别在棱 DD1 , BB1 上,且 2DE=ED1 , BF=2FB1 .证明:
(1)当 AB=BC 时, EF⊥AC ;
(2)点 C1 在平面 AEF 内.
18.设有下列四个命题:
p1:两两相交且不过同一点的三条直线必在同一平面内.
p2:过空间中任意三点有且仅有一个平面.
p3:若空间两条直线不相交,则这两条直线平行.
p4:若直线l ? 平面α,直线m⊥平面α,则m⊥l.
则下述命题中所有真命题的序号是________.
① p1∧p4 ② p1∧p2 ③ ?p2∨p3 ④ ?p3∨?p4
【参考答案】
1.【答案】 C
2.【答案】 C
3.【答案】 C
4.【答案】 C
5.【答案】 D
6.【答案】 D
7.【答案】 A
8.【答案】 C
9.【答案】 D
10.【答案】 C
二、培优提升
11.【答案】 ①④
12.【答案】 ①②
13.【答案】 2
14.【答案】 (1)解:直线 l 与平面 ABCD 平行.理由如下:
由已知, AB//CD , AB? 平面 CDP , CD? 平面 CDP ,
则 AB// 平面 CDP ,
又 l 为平面 ABP 与平面 CDP 的交线, AB? 平面 ABP ,
则 l//AB ,
又 l? 平面 ABCD , AB? 平面 ABCD ,
所以 l/ 平面 ABCD .
(2)证明:连接 BD , ∵ 菱形 ABCD 中, ∠BAD=π3 ,
∴ △ABD 为等边三角形,
又 M 为 BC 中点, ∴ DM⊥AB ,
又 PA=PB ,则 PM⊥AB ,
又 DM∩PM=M , ∴ AB⊥ 平面 PMD ,
又 AB//CD , ∴ CD⊥ 平面 PMD ,
又 CD? 平面 PCD , ∴ 平面 PCD⊥ 平面 PMD .
(3)解: ∵ 平面 PAB⊥ 平面 ABCD ,平面 PAB∩ 平面 ABCD=AB ,
因为 PM⊥AB , PM? 平面 PAB , ∴ PM⊥ 平面 ABCD ,
以 M 为原点, MB , MD , MP 所在直线分别为 x 轴, y 轴, z 轴建立空间直角坐标系,
设 PM=a ,则 P(0,0,a) , A(?1,0,0) , D(0,3,0) ,
则 AD=(1,3,0) , AP=(1,0,a) ,
设平面 ADP 的一个法向量为 n=(x,y,z) ,
则 {AD?n=0AP?n=0 ,即 {x+3y=0x+az=0 ,可取 n=(3a,?a,?3) ,
又平面 PAB 的法向量可取 m=(0,1,0) ,
由题意得 |cos?m,n?|=|m?n||m||n|=a4a2+3=55 ,
解得 a=3 ,即 PM=3 ,
又菱形 ABCD 的面积为 AB×DM=23 ,
∴ 四棱锥 P?ABCD 的体积为 V=13×SABCD×PM=13×23×3=2 .
15.【答案】 (1)解:③ AO1// 面 DBC1 ,如图所示:
连接BD,AC交于点O,连接 OC1 ,
因为 AO//O1C1,AO=O1C1 ,
所以 AOC1O1 是平行四边形,
所以 AO1//OC1 ,又 AO1? 面 DBC1 , OC1? 面 DBC1 ,
所以 AO1// 面 DBC1 .
(2)解:如图所示:
因为过 A 、 C1 、 M 作一截面,交 DD1 于点 G ,且M为中点,
所以G为中点,由正方体知: AM//GC1,AM=GC1 ,
所以截面 AMC1G 是平行四边形,又 AM=AG ,
所以截面 AMC1G 是菱形,连接 AC1,MG,AC1⊥MG ,
所以截面 AMC1G 的面积为: 12AC1?MG=12×23×22=26 .
16.【答案】 (1)证明:由已知得AD ∥ BE,CG ∥ BE,
所以AD ∥ CG,
AD,CG确定一个平面,
从而A,C,G,D四点共面
(2)证明:由已知得AB ⊥ BE,AB ⊥ BC, BE∩BC=B ,
AB ⊥ 平面BCGE.
又因为AB ? 平面ABC,
所以平面ABC ⊥ 平面BCGE.
17.【答案】 (1)解:因为长方体 ABCD?A1B1C1D1 ,所以 BB1 ⊥ 平面 ABCD∴ AC⊥BB1 ,
因为长方体 ABCD?A1B1C1D1,AB=BC ,所以四边形 ABCD 为正方形 ∴AC⊥BD
因为 BB1∩BD=B,BB1、BD? 平面 BB1D1D ,因此 AC⊥ 平面 BB1D1D ,
因为 EF? 平面 BB1D1D ,所以 AC⊥EF
(2)解:在 CC1 上取点M使得 CM=2MC1 ,连 DM,MF ,
因为 D1E=2ED,DD1//CC1,DD1=CC1 ,所以 ED=MC1,ED//MC1,
所以四边形 DMC1E 为平行四边形, ∴DM//EC1
因为 MF//DA,MF=DA, 所以四边形 MFAD 为平行四边形, ∴DM//AF,∴EC1//AF
因此 C1 在平面 AEF 内
18.【答案】 ①③④
【专题训练】
【基础巩固】
1.如果空间四点A,B,C,D不共面,那么下列判断中正确的是(??? )
A.?A,B,C,D四点中必有三点共线
B.?直线 AB 与 CD 相交
C.?A,B,C,D四点中不存在三点共线
D.?直线 AB 与 CD 平行
2.设l为一条直线, α,β 是两个不同的平面,下列命题正确的是(??? )
A.?若 α⊥β,l//α ,则 l⊥β
B.?若 l//α , l//β ,则 α//β
C.?若 l⊥α,l⊥β ,则 α//β
D.?若 l⊥α,l//β ,则 α//β
3.在空间直角坐标系中,若直线l的方向向量为 a=(1,?2,1) ,平面 α 的法向量为 n=(2,3,4) ,则(??? )
A.?l//α?????????????????????????????B.?l⊥α?????????????????????????????C.?l?α 或 l//α?????????????????????????????D.?l与 α 斜交
4.已知m,n为两条不同的直线, α//β 是两个不同的平面,下列命题为真命题的是(??? )
A.?m⊥n,m//α?n⊥α??????????????????????????????????????B.?n//β,β⊥α?n⊥α
C.?m//n,m⊥β?n⊥β??????????????????????????????????????D.?m//α,n?α?m//n
5.已知m,n为两条不同的直线, α,β 是两个不同的平面,给出下列4个命题:
① m⊥n,m//α?n⊥α ;② n//β,β⊥α?n⊥α ;③ m//n,m⊥β?n⊥β ;④ m//α,n⊥α?m⊥n .其中所有真命题的序号是(??? )
A.?①③?????????????????????????????????????B.?②④?????????????????????????????????????C.?②③?????????????????????????????????????D.?③④
6.已知P,Q是不同的点,l,m,n是不同的直线, α , β 是不同的平面,则下列数学符号表示的命题中,不是公理的是(??? )
A.?P∈l , Q∈l , P∈α , Q∈α?l?α
B.?P∈α , P∈β? 存在唯一直线l, α∩β=l ,且 P∈l
C.?l//m , m//n?l//n
D.?m⊥α , n⊥α?m//n
7.设 α , β 是两个不同的平面, l 是一条直线,以下结论正确的是(??? )
A.?若 l⊥α , α//β ,则 l⊥β
B.?若 l//α , l//β ,则 α//β
C.?若 l⊥α , α⊥β ,则 l?β
D.?若 l//α , α⊥β ,则 l⊥β
8.已知正方体 ABCD?A1B1C1D1 的棱长为3,E,F,G分别为棱 AA1 , AB , CC1 上的点,其中 AE=1 , AF=2 , CG=32 ,平面 α 经过点E,F,G,则 α 截此正方体所得的截面为(??? )
A.?三角形????????????????????????????????B.?四边形????????????????????????????????C.?五边形????????????????????????????????D.?六边形
9.下列命题中正确的是(??? )
A.?三点确定一个平面
B.?垂直于同一直线的两条直线平行
C.?若直线 l 与平面 α 上的无数条直线都垂直,则直线 l⊥α
D.?若 a、b、c 是三条直线, a//b 且与 c 都相交,则直线 a、b、c 共面.
10.已知 a,b 是两条直线, α,β 是两个平面,则 a⊥b 的一个充分条件是(??? )
A.?a⊥α , b//β , α⊥β???????????????????????????????????B.?a⊥α , b⊥β , α//β
C.?a?α , b⊥β , α//β???????????????????????????????????D.?a?α , b//β , α⊥β
【培优提升】
11.已知 α,β 是两个不同的平面, l,m 是两条不同的直线, l⊥α,m?β .给出下列命题:
① α//β?l⊥m ;② α⊥β?l//m ;③ m//α?l⊥β ;④ l⊥β?m//α .
其中正确的命题是________.
12.如图所示,在直角梯形 ABCD 中, BC⊥DC,AE⊥DC,M,N 分别是 AD,BE 的中点,将三角形 ADE 沿 AE 折起,下列说法正确的是________(填上所有正确的序号).
①不论 D 折至何位置(不在平面 ABC 内)都有 MN∥ 平面 DEC ;
②不论 D 折至何位置都有 MN⊥AE ;
③不论 D 折至何位置(不在平面 ABC 内)都有 MN∥AB .
13.下列说法中正确的有________个.
①空间中三条直线交于一点,则这三条直线共面;
②一个平行四边形确定一个平面;
③若一个角的两边分别平行于另一个角的两边,则这两个角相等;
④已知两个不同的平面 α 和 β ,若 A∈α , A∈β ,且 α∩β=l ,则点A在直线 l 上.
14.在四棱锥 P?ABCD 中,底面 ABCD 是边长为2的菱形, ∠ABC=120° , PA=PB , M 为 AB 中点,设 l 为平面 ABP 与平面 CDP 的交线.
(1)判断直线 l 与平面 ABCD 的位置关系,并说明理由;
(2)求证:平面 PCD⊥ 平面 PMD ;
(3)若平面 PAB⊥ 平面 ABCD ,且二面角 B?AP?D 的余弦值为 55 ,求四棱锥 P?ABCD 的体积.
15.已知正方体 ABCD?A1B1C1D1 中的棱长为2, O1 是 A1C1 中点.则一定有__________.
(1)在下面三个选项中选取一个正确的序号填写在横线上,并说明理由.
① AO1? 面 DBC1 ② AO1 与平面 DBC1 相交??????????? ③ AO1// 面 DBC1
(2)设 BB1 的中点为 M ,过 A 、 C1 、 M 作一截面,交 DD1 于点 G ,求截面 AMC1G 面积.
16.图1是由矩形 ADEB . RtΔABC 和菱形 BFGC 组成的一个平面图形,其中 BE=BF ,将其沿 AB , BC 折起使得 BE 与 BF 重合,连结 DG ,如图2.
(1)证明:图2中的 A,C,G,D 四点共面;
(2)证明:平面 ABC⊥ 平面 BCGE .
17.如图,在长方体 ABCD?A1B1C1D1 中,点E,F分别在棱 DD1 , BB1 上,且 2DE=ED1 , BF=2FB1 .证明:
(1)当 AB=BC 时, EF⊥AC ;
(2)点 C1 在平面 AEF 内.
18.设有下列四个命题:
p1:两两相交且不过同一点的三条直线必在同一平面内.
p2:过空间中任意三点有且仅有一个平面.
p3:若空间两条直线不相交,则这两条直线平行.
p4:若直线l ? 平面α,直线m⊥平面α,则m⊥l.
则下述命题中所有真命题的序号是________.
① p1∧p4 ② p1∧p2 ③ ?p2∨p3 ④ ?p3∨?p4
【参考答案】
1.【答案】 C
2.【答案】 C
3.【答案】 C
4.【答案】 C
5.【答案】 D
6.【答案】 D
7.【答案】 A
8.【答案】 C
9.【答案】 D
10.【答案】 C
二、培优提升
11.【答案】 ①④
12.【答案】 ①②
13.【答案】 2
14.【答案】 (1)解:直线 l 与平面 ABCD 平行.理由如下:
由已知, AB//CD , AB? 平面 CDP , CD? 平面 CDP ,
则 AB// 平面 CDP ,
又 l 为平面 ABP 与平面 CDP 的交线, AB? 平面 ABP ,
则 l//AB ,
又 l? 平面 ABCD , AB? 平面 ABCD ,
所以 l/ 平面 ABCD .
(2)证明:连接 BD , ∵ 菱形 ABCD 中, ∠BAD=π3 ,
∴ △ABD 为等边三角形,
又 M 为 BC 中点, ∴ DM⊥AB ,
又 PA=PB ,则 PM⊥AB ,
又 DM∩PM=M , ∴ AB⊥ 平面 PMD ,
又 AB//CD , ∴ CD⊥ 平面 PMD ,
又 CD? 平面 PCD , ∴ 平面 PCD⊥ 平面 PMD .
(3)解: ∵ 平面 PAB⊥ 平面 ABCD ,平面 PAB∩ 平面 ABCD=AB ,
因为 PM⊥AB , PM? 平面 PAB , ∴ PM⊥ 平面 ABCD ,
以 M 为原点, MB , MD , MP 所在直线分别为 x 轴, y 轴, z 轴建立空间直角坐标系,
设 PM=a ,则 P(0,0,a) , A(?1,0,0) , D(0,3,0) ,
则 AD=(1,3,0) , AP=(1,0,a) ,
设平面 ADP 的一个法向量为 n=(x,y,z) ,
则 {AD?n=0AP?n=0 ,即 {x+3y=0x+az=0 ,可取 n=(3a,?a,?3) ,
又平面 PAB 的法向量可取 m=(0,1,0) ,
由题意得 |cos?m,n?|=|m?n||m||n|=a4a2+3=55 ,
解得 a=3 ,即 PM=3 ,
又菱形 ABCD 的面积为 AB×DM=23 ,
∴ 四棱锥 P?ABCD 的体积为 V=13×SABCD×PM=13×23×3=2 .
15.【答案】 (1)解:③ AO1// 面 DBC1 ,如图所示:
连接BD,AC交于点O,连接 OC1 ,
因为 AO//O1C1,AO=O1C1 ,
所以 AOC1O1 是平行四边形,
所以 AO1//OC1 ,又 AO1? 面 DBC1 , OC1? 面 DBC1 ,
所以 AO1// 面 DBC1 .
(2)解:如图所示:
因为过 A 、 C1 、 M 作一截面,交 DD1 于点 G ,且M为中点,
所以G为中点,由正方体知: AM//GC1,AM=GC1 ,
所以截面 AMC1G 是平行四边形,又 AM=AG ,
所以截面 AMC1G 是菱形,连接 AC1,MG,AC1⊥MG ,
所以截面 AMC1G 的面积为: 12AC1?MG=12×23×22=26 .
16.【答案】 (1)证明:由已知得AD ∥ BE,CG ∥ BE,
所以AD ∥ CG,
AD,CG确定一个平面,
从而A,C,G,D四点共面
(2)证明:由已知得AB ⊥ BE,AB ⊥ BC, BE∩BC=B ,
AB ⊥ 平面BCGE.
又因为AB ? 平面ABC,
所以平面ABC ⊥ 平面BCGE.
17.【答案】 (1)解:因为长方体 ABCD?A1B1C1D1 ,所以 BB1 ⊥ 平面 ABCD∴ AC⊥BB1 ,
因为长方体 ABCD?A1B1C1D1,AB=BC ,所以四边形 ABCD 为正方形 ∴AC⊥BD
因为 BB1∩BD=B,BB1、BD? 平面 BB1D1D ,因此 AC⊥ 平面 BB1D1D ,
因为 EF? 平面 BB1D1D ,所以 AC⊥EF
(2)解:在 CC1 上取点M使得 CM=2MC1 ,连 DM,MF ,
因为 D1E=2ED,DD1//CC1,DD1=CC1 ,所以 ED=MC1,ED//MC1,
所以四边形 DMC1E 为平行四边形, ∴DM//EC1
因为 MF//DA,MF=DA, 所以四边形 MFAD 为平行四边形, ∴DM//AF,∴EC1//AF
因此 C1 在平面 AEF 内
18.【答案】 ①③④
同课章节目录
- 第六章 平面向量及其应用
- 6.1 平面向量的概念
- 6.2 平面向量的运算
- 6.3 平面向量基本定理及坐标表示
- 6.4 平面向量的应用
- 第七章 复数
- 7.1 复数的概念
- 7.2 复数的四则运算
- 7.3 * 复数的三角表示
- 第八章 立体几何初步
- 8.1 基本立体图形
- 8.2 立体图形的直观图
- 8.3 简单几何体的表面积与体积
- 8.4 空间点、直线、平面之间的位置关系
- 8.5 空间直线、平面的平行
- 8.6 空间直线、平面的垂直
- 第九章 统计
- 9.1 随机抽样
- 9.2 用样本估计总体
- 9.3 统计分析案例 公司员工
- 第十章 概率
- 10.1 随机事件与概率
- 10.2 事件的相互独立性
- 10.3 频率与概率
