6.3平面向量基本定理及坐标表示-【新教材】2020-2021学年人教A版(2019)高中数学必修第二册专题训练(Word版含答案)
文档属性
| 名称 | 6.3平面向量基本定理及坐标表示-【新教材】2020-2021学年人教A版(2019)高中数学必修第二册专题训练(Word版含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 53.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-04-19 00:00:00 | ||
图片预览


文档简介
高一数学人教版(2019)必修第二册
【6.3平面向量基本定理及坐标表示专题训练】
【基础巩固】
1.若平面向量 a 与 b 满足: |a|=2,|b|=1,|a+b|=7 则 a 与 b 的夹角为(??? )
A.?30°??????????????????????????????????????B.?45°??????????????????????????????????????C.?60°??????????????????????????????????????D.?120°
2.在平面直角坐标系中,以 O(0,0) , A(1,1) , B(3,0) 为顶点构造平行四边形,下列各项中不能作为平行四边形第四个顶点坐标的是(??? )
A.?(?3,1)????????????????????????????????B.?(4,1)????????????????????????????????C.?(?2,1)????????????????????????????????D.?(2,?1)
3.若过点 P(3,2m) 和点 Q(?m,2) 的直线与方向向量为 a=(?5,5) 的直线平行,则实数 m 的值是(?? )
A.?13?????????????????????????????????????????B.??13?????????????????????????????????????????C.?2?????????????????????????????????????????D.?-2
4.过 A4,y , B(2,?3) 两点的直线的一个方向向量为 n=(?1,?1) 则 y= (??? )
A.??32???????????????????????????????????????B.?32???????????????????????????????????????C.?-1???????????????????????????????????????D.?1
5.设平面 α 与平面 β 的夹角为 θ ,若平面 α,β 的法向量分别为 n1,n2 ,则 |cosθ|= (??? )
A.?n1?n2|n1||n2|?????????????????????????????????B.?|n1?n2||n1||n2|?????????????????????????????????C.?|n1||n2|n1?n2?????????????????????????????????D.?|n1||n2||n1?n2|
6.已知向量 a=(2,1,?5) , b=(4,y,z) ,且 a//b ,则 y+z= (??? )
A.?-8?????????????????????????????????????????B.?-12?????????????????????????????????????????C.?8?????????????????????????????????????????D.?12
7.已知向量 a=(4,4,5) , b=(?7,x,y) 分别是直线 l1 、 l2 的方向向量,若 l1⊥l2 ,则下列几组解中可能正确的是(??? )
A.?x=2,y=4??????????????????????B.?x=4,y=3??????????????????????C.?x=1,y=3??????????????????????D.?x=6,y=2
8.如图,在棱长为1的正方体 ABCD?A1B1C1D1 中,点M是底面正方形 ABCD 的中心,点P是底面 ABCD 所在平面内的一个动点,且满足 ∠MC1P=30° ,则动点P的轨迹为(??? )
A.?圆????????????????????????????????????B.?抛物线????????????????????????????????????C.?双曲线????????????????????????????????????D.?椭圆
9.已知向量 a=(?2,1),b=(3,5) ,则 a?2b= (??? )
A.?(?8,?9)??????????????????????????B.?(?4,?9)??????????????????????????C.?(?5,?6)??????????????????????????D.?(8,11)
10.已知 e1,e2 是单位向量, e1?e2=?23 ,若平面向量 a 满足 a?e1=1 , a?e2=2 且 a=xe1+ye2 ,则 x+y= (??? )
A.?9???????????????????????????????????????????B.?8???????????????????????????????????????????C.?7???????????????????????????????????????????D.?6
【培优提升】
11.若 A(0,2,198) , B(1,?1,58) , C(?2,1,58) 是平面内的三点,设平面的法向量 a=(x,y,z) ,则 x:y:z= ________.
12.已知正方体 ABCD?A1B1C1D1 的棱长为4,M、N、P分别在棱 AB 、 BC 、 CC1 上,且 AM=1,BN=2,CP=3 .过M、N、P三点的平面交 AC1 于点Q,则A、Q两点间的距离为________.
13.设 △OAB 中, OA=a , OB=b 且满足 |a?b|=|a| , |a+b|=2 ,当 △OAB 面积最大时,则 a+b 与 b 夹角的大小是________.
14.如图,在四边形 ABCD 中, ∠B=60° , AB=2 , BC=6 , AD=1 ,若M,N是线段 BC 上的动点,且 |MN|=1 ,则 DM?DN 的取值范围为________.
15.已知平面向量 a=(3,?2) , b=(1,?m) 且 b?a 与 c=(2,1) 共线.
(1)求 m 的值;
(2)a+λb 与 a?b 垂直,求实数 λ 的值.
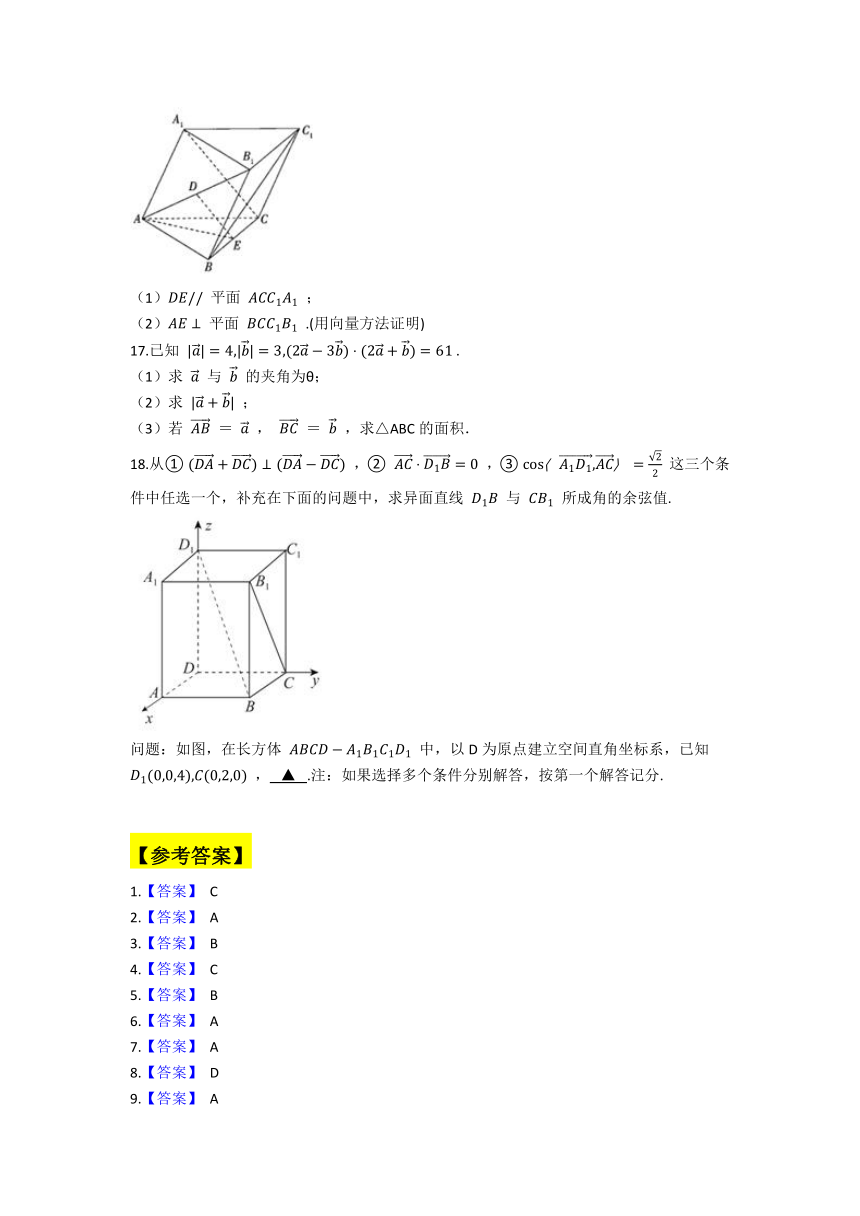
16.如图,在三棱柱 ABC?A1B1C1 中, AB=AC,A1C⊥BC1,AB1⊥BC1 ,D,E分别是 AB1,BC 的中点.求证:
(1)DE// 平面 ACC1A1 ;
(2)AE⊥ 平面 BCC1B1 .(用向量方法证明)
17.已知 |a|=4,|b|=3,(2a?3b)?(2a+b)=61 .
(1)求 a 与 b 的夹角为θ;
(2)求 |a+b| ;
(3)若 AB = a , BC = b ,求△ABC的面积.
18.从① (DA+DC)⊥(DA?DC) ,② AC?D1B=0 ,③ cos?A1D1,AC?=22 这三个条件中任选一个,补充在下面的问题中,求异面直线 D1B 与 CB1 所成角的余弦值.
问题:如图,在长方体 ABCD?A1B1C1D1 中,以D为原点建立空间直角坐标系,已知 D1(0,0,4),C(0,2,0) ,? ▲? .注:如果选择多个条件分别解答,按第一个解答记分.
【参考答案】
1.【答案】 C
2.【答案】 A
3.【答案】 B
4.【答案】 C
5.【答案】 B
6.【答案】 A
7.【答案】 A
8.【答案】 D
9.【答案】 A
10.【答案】 A
11.【答案】 2:3:(-4)
12.【答案】 23
13.【答案】 31010
14.【答案】 [114,15]
15.【答案】 (1)解:由题意得: b?a=(?2,2?m) , c=(2,1)
因为 b?a 与 c=(2,1) 共线
所以 (?2)×1?2(2?m)=0 ,
解得 m=3
(2)解:由(1)可知 b=(1,?3) ,于是 a+λb=(3+λ,?2?3λ) ,
而 a?b=(2,1) ,
由于 (a+λb)⊥(a?b) ,
从而 2(3+λ)?(2+3λ)=0 ,
解得: λ=4
16.【答案】 (1)证明:设 AB=a,AC=b,AA1=c .
DE=AE?AD=12(a+b)?12AB1=12(a+b)?12(a+c)=12(b?c) ,
∵ A1C=AC?AA1=b?c ,
∴ DE=12A1C ,
∴ DE//A1C ,又 DE? 平面 ACC1A1,A1C? 平面 ACC1A1 ,
∴ DE// 平面 ACC1A1
(2)证明:易知 AE=12(a+b),BC=b?a,BB1=c,BC1=b?a+c,AB1=a+c ,
∵ A1C⊥BC1,AB1⊥BC1 ,
∴ {A1C?BC1=0AB1?BC1=0
即 {(b?c)?(b?a+c)=0,(a+c)?(b?a+c)?0,
两式相加,整理得 b2?a2+b?c+a?c=0 ,
∵ AB=AC ,
∴ |a|=|b| ,
∴ b?c+a?c=0 .
∵ AE?BB1=12(a+b)?c=12(a?c+b?c)=0 ,
∴ AE⊥BB1 .
又 AE?BC=12(b2?a2)=0 ,
∴ AE⊥BC .
又 BC∩BB1=B ,
∴ AE⊥ 平面 BCC1B1
17.【答案】 (1)解:因为 (2a?3b)?(2a+b)=61 ,
所以 4|a|2?4a?b?3|b|2=61 .
又 |a|=4,|b|=3 ,
所以 64?4a?b?27=61 ,
所以 a?b=?6 ,
所以 cosθ=a?b|a||b|=?64×3=?12 .
又0≤θ≤π,所以 θ=2π3
(2)解: |a+b|2=(a+b)2=|a|2+2a?b+|b|2
=42+2×(-6)+32=13,所以 |a+b|=13
(3)解:因为 AB 与 BC 的夹角 θ=2π3 ,
所以∠ABC= π?2π3=π3 .
又 |AB|=|a|=4,|BC|=|b|=3 ,
所以S△ABC= 12×4×3×32=33
18.【答案】 解:选①.
∵ (DA+DC)⊥(DA?DC) ,
∴ (DA+DC)?(DA?DC)=0 ,
∴ DA2?DC2=0 ,
即 DA=DC=2 .
∴ B(2,2,0),B1(2,2,4) ,
∴ D1B=(2,2,?4),CB1=(2,0,4) ,
∵ cos=D1B?CB1→|D1B|?|CB1|=?1226×25=?3010 ,
∴异面直线 D1B 与 CB1 所成角的余弦值为 3010 .
选②.
设 A(a,0,0) ,其中 a>0 ,
从而 B(a,2,0),B1(a,2,4) ,
∴ AC=(?a,2,0),D1B=(a,2,?4) .
∵ AC?D1B=0 ,∴ ?a2+4=0 ,
由于 a>0 ,所以 a=2 .
∴ D1B=(2,2,?4),CB1=(2,0,4) ,
∴ cos?D1B,CB1?=D1B?CB1|D1B|?|CB1|=?1226×25=?3010 ,
∴异面直线 D1B 与 CB1 所成角的余弦值为 3010 .
选③.
cos?A1D1,AC?=cos?AD,AC?=22 ,
∴ ∠DAC=45° ,
∴ DA=DC=2 .
解法同①.
【6.3平面向量基本定理及坐标表示专题训练】
【基础巩固】
1.若平面向量 a 与 b 满足: |a|=2,|b|=1,|a+b|=7 则 a 与 b 的夹角为(??? )
A.?30°??????????????????????????????????????B.?45°??????????????????????????????????????C.?60°??????????????????????????????????????D.?120°
2.在平面直角坐标系中,以 O(0,0) , A(1,1) , B(3,0) 为顶点构造平行四边形,下列各项中不能作为平行四边形第四个顶点坐标的是(??? )
A.?(?3,1)????????????????????????????????B.?(4,1)????????????????????????????????C.?(?2,1)????????????????????????????????D.?(2,?1)
3.若过点 P(3,2m) 和点 Q(?m,2) 的直线与方向向量为 a=(?5,5) 的直线平行,则实数 m 的值是(?? )
A.?13?????????????????????????????????????????B.??13?????????????????????????????????????????C.?2?????????????????????????????????????????D.?-2
4.过 A4,y , B(2,?3) 两点的直线的一个方向向量为 n=(?1,?1) 则 y= (??? )
A.??32???????????????????????????????????????B.?32???????????????????????????????????????C.?-1???????????????????????????????????????D.?1
5.设平面 α 与平面 β 的夹角为 θ ,若平面 α,β 的法向量分别为 n1,n2 ,则 |cosθ|= (??? )
A.?n1?n2|n1||n2|?????????????????????????????????B.?|n1?n2||n1||n2|?????????????????????????????????C.?|n1||n2|n1?n2?????????????????????????????????D.?|n1||n2||n1?n2|
6.已知向量 a=(2,1,?5) , b=(4,y,z) ,且 a//b ,则 y+z= (??? )
A.?-8?????????????????????????????????????????B.?-12?????????????????????????????????????????C.?8?????????????????????????????????????????D.?12
7.已知向量 a=(4,4,5) , b=(?7,x,y) 分别是直线 l1 、 l2 的方向向量,若 l1⊥l2 ,则下列几组解中可能正确的是(??? )
A.?x=2,y=4??????????????????????B.?x=4,y=3??????????????????????C.?x=1,y=3??????????????????????D.?x=6,y=2
8.如图,在棱长为1的正方体 ABCD?A1B1C1D1 中,点M是底面正方形 ABCD 的中心,点P是底面 ABCD 所在平面内的一个动点,且满足 ∠MC1P=30° ,则动点P的轨迹为(??? )
A.?圆????????????????????????????????????B.?抛物线????????????????????????????????????C.?双曲线????????????????????????????????????D.?椭圆
9.已知向量 a=(?2,1),b=(3,5) ,则 a?2b= (??? )
A.?(?8,?9)??????????????????????????B.?(?4,?9)??????????????????????????C.?(?5,?6)??????????????????????????D.?(8,11)
10.已知 e1,e2 是单位向量, e1?e2=?23 ,若平面向量 a 满足 a?e1=1 , a?e2=2 且 a=xe1+ye2 ,则 x+y= (??? )
A.?9???????????????????????????????????????????B.?8???????????????????????????????????????????C.?7???????????????????????????????????????????D.?6
【培优提升】
11.若 A(0,2,198) , B(1,?1,58) , C(?2,1,58) 是平面内的三点,设平面的法向量 a=(x,y,z) ,则 x:y:z= ________.
12.已知正方体 ABCD?A1B1C1D1 的棱长为4,M、N、P分别在棱 AB 、 BC 、 CC1 上,且 AM=1,BN=2,CP=3 .过M、N、P三点的平面交 AC1 于点Q,则A、Q两点间的距离为________.
13.设 △OAB 中, OA=a , OB=b 且满足 |a?b|=|a| , |a+b|=2 ,当 △OAB 面积最大时,则 a+b 与 b 夹角的大小是________.
14.如图,在四边形 ABCD 中, ∠B=60° , AB=2 , BC=6 , AD=1 ,若M,N是线段 BC 上的动点,且 |MN|=1 ,则 DM?DN 的取值范围为________.
15.已知平面向量 a=(3,?2) , b=(1,?m) 且 b?a 与 c=(2,1) 共线.
(1)求 m 的值;
(2)a+λb 与 a?b 垂直,求实数 λ 的值.
16.如图,在三棱柱 ABC?A1B1C1 中, AB=AC,A1C⊥BC1,AB1⊥BC1 ,D,E分别是 AB1,BC 的中点.求证:
(1)DE// 平面 ACC1A1 ;
(2)AE⊥ 平面 BCC1B1 .(用向量方法证明)
17.已知 |a|=4,|b|=3,(2a?3b)?(2a+b)=61 .
(1)求 a 与 b 的夹角为θ;
(2)求 |a+b| ;
(3)若 AB = a , BC = b ,求△ABC的面积.
18.从① (DA+DC)⊥(DA?DC) ,② AC?D1B=0 ,③ cos?A1D1,AC?=22 这三个条件中任选一个,补充在下面的问题中,求异面直线 D1B 与 CB1 所成角的余弦值.
问题:如图,在长方体 ABCD?A1B1C1D1 中,以D为原点建立空间直角坐标系,已知 D1(0,0,4),C(0,2,0) ,? ▲? .注:如果选择多个条件分别解答,按第一个解答记分.
【参考答案】
1.【答案】 C
2.【答案】 A
3.【答案】 B
4.【答案】 C
5.【答案】 B
6.【答案】 A
7.【答案】 A
8.【答案】 D
9.【答案】 A
10.【答案】 A
11.【答案】 2:3:(-4)
12.【答案】 23
13.【答案】 31010
14.【答案】 [114,15]
15.【答案】 (1)解:由题意得: b?a=(?2,2?m) , c=(2,1)
因为 b?a 与 c=(2,1) 共线
所以 (?2)×1?2(2?m)=0 ,
解得 m=3
(2)解:由(1)可知 b=(1,?3) ,于是 a+λb=(3+λ,?2?3λ) ,
而 a?b=(2,1) ,
由于 (a+λb)⊥(a?b) ,
从而 2(3+λ)?(2+3λ)=0 ,
解得: λ=4
16.【答案】 (1)证明:设 AB=a,AC=b,AA1=c .
DE=AE?AD=12(a+b)?12AB1=12(a+b)?12(a+c)=12(b?c) ,
∵ A1C=AC?AA1=b?c ,
∴ DE=12A1C ,
∴ DE//A1C ,又 DE? 平面 ACC1A1,A1C? 平面 ACC1A1 ,
∴ DE// 平面 ACC1A1
(2)证明:易知 AE=12(a+b),BC=b?a,BB1=c,BC1=b?a+c,AB1=a+c ,
∵ A1C⊥BC1,AB1⊥BC1 ,
∴ {A1C?BC1=0AB1?BC1=0
即 {(b?c)?(b?a+c)=0,(a+c)?(b?a+c)?0,
两式相加,整理得 b2?a2+b?c+a?c=0 ,
∵ AB=AC ,
∴ |a|=|b| ,
∴ b?c+a?c=0 .
∵ AE?BB1=12(a+b)?c=12(a?c+b?c)=0 ,
∴ AE⊥BB1 .
又 AE?BC=12(b2?a2)=0 ,
∴ AE⊥BC .
又 BC∩BB1=B ,
∴ AE⊥ 平面 BCC1B1
17.【答案】 (1)解:因为 (2a?3b)?(2a+b)=61 ,
所以 4|a|2?4a?b?3|b|2=61 .
又 |a|=4,|b|=3 ,
所以 64?4a?b?27=61 ,
所以 a?b=?6 ,
所以 cosθ=a?b|a||b|=?64×3=?12 .
又0≤θ≤π,所以 θ=2π3
(2)解: |a+b|2=(a+b)2=|a|2+2a?b+|b|2
=42+2×(-6)+32=13,所以 |a+b|=13
(3)解:因为 AB 与 BC 的夹角 θ=2π3 ,
所以∠ABC= π?2π3=π3 .
又 |AB|=|a|=4,|BC|=|b|=3 ,
所以S△ABC= 12×4×3×32=33
18.【答案】 解:选①.
∵ (DA+DC)⊥(DA?DC) ,
∴ (DA+DC)?(DA?DC)=0 ,
∴ DA2?DC2=0 ,
即 DA=DC=2 .
∴ B(2,2,0),B1(2,2,4) ,
∴ D1B=(2,2,?4),CB1=(2,0,4) ,
∵ cos
∴异面直线 D1B 与 CB1 所成角的余弦值为 3010 .
选②.
设 A(a,0,0) ,其中 a>0 ,
从而 B(a,2,0),B1(a,2,4) ,
∴ AC=(?a,2,0),D1B=(a,2,?4) .
∵ AC?D1B=0 ,∴ ?a2+4=0 ,
由于 a>0 ,所以 a=2 .
∴ D1B=(2,2,?4),CB1=(2,0,4) ,
∴ cos?D1B,CB1?=D1B?CB1|D1B|?|CB1|=?1226×25=?3010 ,
∴异面直线 D1B 与 CB1 所成角的余弦值为 3010 .
选③.
cos?A1D1,AC?=cos?AD,AC?=22 ,
∴ ∠DAC=45° ,
∴ DA=DC=2 .
解法同①.
同课章节目录
- 第六章 平面向量及其应用
- 6.1 平面向量的概念
- 6.2 平面向量的运算
- 6.3 平面向量基本定理及坐标表示
- 6.4 平面向量的应用
- 第七章 复数
- 7.1 复数的概念
- 7.2 复数的四则运算
- 7.3 * 复数的三角表示
- 第八章 立体几何初步
- 8.1 基本立体图形
- 8.2 立体图形的直观图
- 8.3 简单几何体的表面积与体积
- 8.4 空间点、直线、平面之间的位置关系
- 8.5 空间直线、平面的平行
- 8.6 空间直线、平面的垂直
- 第九章 统计
- 9.1 随机抽样
- 9.2 用样本估计总体
- 9.3 统计分析案例 公司员工
- 第十章 概率
- 10.1 随机事件与概率
- 10.2 事件的相互独立性
- 10.3 频率与概率
