8.1基本立体图形-【新教材】2020-2021学年人教A版(2019)高中数学必修第二册同步讲义(word含答案)
文档属性
| 名称 | 8.1基本立体图形-【新教材】2020-2021学年人教A版(2019)高中数学必修第二册同步讲义(word含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 115.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-04-19 00:00:00 | ||
图片预览


文档简介
高一数学人教版(2019)必修第二册
【8.1基本立体图形】
【学习目标】掌握立体图形的结构特征
【难点突破】
知识点1:棱柱的结构特征
一般地,有两个面互相平行,其余各面都是四边形,并且相邻两个四边形的公共边都互侧相平行,由这些面所围成的几何体叫做棱柱.
知识点2:棱锥的结构 一般地,有一个面是多边形,其余各面都是有一个公共顶点的三角形,由这些面所围成的几何体叫做棱锥
知识点3:棱台于圆台的结构特征
用一个平行于棱锥底面的平面去截棱锥,底面和截面之间那部分,这样的几何体叫做棱台
【例题分析】
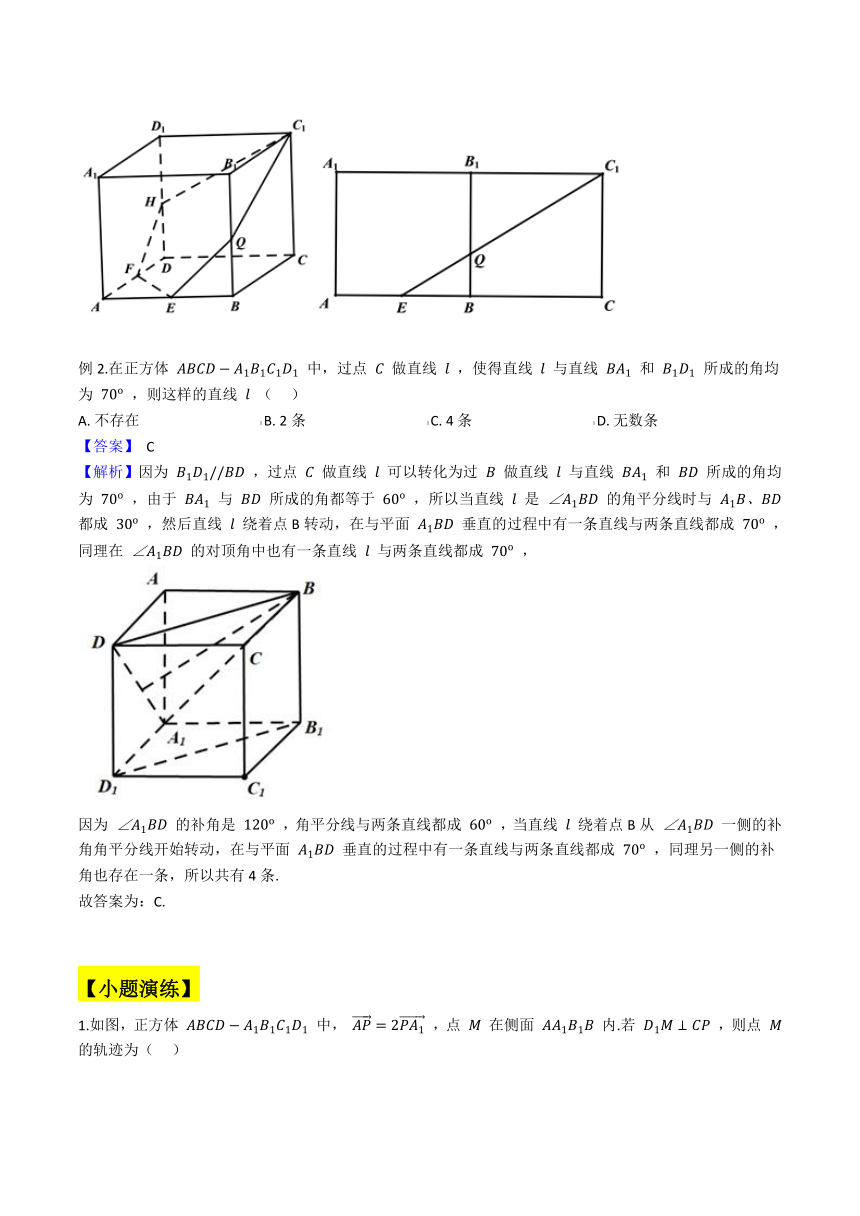
例1.已知正方体 ABCD?A1B1C1D1 的棱长为2, AB , AD 中点分别为 E , F ,若过 EF 的平面截该正方体所得的截面是一个五边形,则该五边形周长的最大值为(??? )
A.?2+213????????????????????????B.?2+13????????????????????????C.?32+25????????????????????????D.?32+5
【答案】 A
【解析】将面 BCC1B1 展开与面 ABB1A1 处于同一平面要使 EQ+QC1+FH+HCl 最大,则沿面 C1QEFH 切才能保证五点共面,在 Rt△ECC1 中, CC1=BC=2,BE=12AB=1 ,此时 EQ+QC1=22+(2+1)2=13 ,又 FH+HC1=EQ+QC=13 ,
∴ 该五边形周长的最大值为 EF+2(EQ+QC1)=2+213。
故答案为:A
例2.在正方体 ABCD?A1B1C1D1 中,过点 C 做直线 l ,使得直线 l 与直线 BA1 和 B1D1 所成的角均为 70o ,则这样的直线 l (??? )
A.?不存在???????????????????????????????????B.?2条???????????????????????????????????C.?4条???????????????????????????????????D.?无数条
【答案】 C
【解析】因为 B1D1//BD ,过点 C 做直线 l 可以转化为过 B 做直线 l 与直线 BA1 和 BD 所成的角均为 70o ,由于 BA1 与 BD 所成的角都等于 60o ,所以当直线 l 是 ∠A1BD 的角平分线时与 A1B、BD 都成 30o ,然后直线 l 绕着点B转动,在与平面 A1BD 垂直的过程中有一条直线与两条直线都成 70o ,同理在 ∠A1BD 的对顶角中也有一条直线 l 与两条直线都成 70o ,
因为 ∠A1BD 的补角是 120o ,角平分线与两条直线都成 60o ,当直线 l 绕着点B从 ∠A1BD 一侧的补角角平分线开始转动,在与平面 A1BD 垂直的过程中有一条直线与两条直线都成 70o ,同理另一侧的补角也存在一条,所以共有4条.
故答案为:C.
【小题演练】
1.如图,正方体 ABCD?A1B1C1D1 中, AP=2PA1 ,点 M 在侧面 AA1B1B 内.若 D1M⊥CP ,则点 M 的轨迹为(?? ?)
A.?线段?????????????????????????????B.?圆弧?????????????????????????????C.?抛物线一部分?????????????????????????????D.?椭圆一部分
2.已知正三棱柱 ABC?A1B1C1 ,的体积为 163 ,底面积为 43 ,则三棱柱 ABC?A1B1C1 的外接球表面积为(??? )
A.?1123π???????????????????????????????????B.?563π???????????????????????????????????C.?2243π???????????????????????????????????D.?28π
3.在三棱锥 P?ABC 中, PA⊥ 平面 ABC , AP=2 , AB=22 , AC=4 , ∠BAC=45° ,则三棱锥 P?ABC 外接球的表面积是(??? )
A.?14π?????????????????????????????????????B.?16π?????????????????????????????????????C.?18π?????????????????????????????????????D.?20π
4.如图,在侧棱垂直底面的三棱柱 ABC?A1B1C1 中, ∠BAC=90° , AB=AC=22AA1 , D , E 分别是棱 AB , B1C1 的中点, F 是棱 CC1 上的一动点,记二面角 D?EF?B 的大小为 α ,则在 F 从 C1 运动到 C 的过程中, α 的变化情况为(??? )
A.?增大???????????????????????????B.?减小???????????????????????????C.?先增大再减小???????????????????????????D.?先减小再增大
5.在空间中,两个不同平面把空间最少可分成________部分,最多可分成________部分.
6.已知球 O1 是棱长为2的正方体 ABCD?A1B1C1D1 的内切球,球 O2 (在正方体 ABCD?A1B1C1D1 内部)与平面 ABCD ,平面 ABB1A1 和平面 ADD1A1 都相切,并且与球 O1 相切,则球 O1 与球 O2 的半径之比为________.
【参考答案】
1.【答案】 A
【解析】如图建立空间直角坐标系,
设棱长为3, P(3,0,2) , C(0,3,0) , D1(0,0,3) , M(3,y,z) , D1M=(3,y,z?3) , CP=(3,?3,2) ,
D1M?CP=9?3y+2(z?3)=0 ,整理为: 3y?2z?3=0 ,
所以点 M 的轨迹方程是关于 y,z 的二元一次方程,所以点M的轨迹是平面 ABB1A1 平面内,直线 3y?2z?3=0 内的一段线段。
故答案为:A
2.【答案】 A
【解析】依题意, AA1=16343=4 ,而 S△ABC=12AB×AC×sinA=34AB2=43 ,
解得 AB=4 ,记 △ABC 的中心为О, △A1B1C1 的中心为О1 , 则 AA1=OO1=4 ,
取 OO1 的中点 D ,因为 AO=CO , ∠AOD=∠COD=90? ,由勾股定理得 AD=CD ,
同理可得 AD=BD=A1D=B1D=C1D ,
所以正三棱柱的外接球的球心为即 D , AD 为外接球的半径,
由正弦定理得 AO=AB2sin60?=433 ,
故 AD2=OD2+AO2=4+163=283 ,
故三棱柱 ABC?A1B1C1 的外接球表面积 S=4πR2=4π×283=1123π ,
故答案为:A.
3.【答案】 D
【解析】在 △BAC 中, ∠BAC=45° , AB=22 , AC=4 ,
由余弦定理可得 BC2=AB2+AC2?2AB?ACcosπ4=8+16?2×4×22×22=22 ,
则 BC2+AB2=AC2 ,所以 BC⊥AB ,
由 PA⊥ 平面 ABC ,则 PA⊥BC , PA∩AB=A ,
所以 BC⊥ 平面 PAB ,
所以 BC⊥PB ,
所以 △PBC 为直角三角形,
又 △PAC 为直角三角形,
所以 PC 是外接球直径,O是 PC 的中点,即为球心,
又 AB=BC=22,?PA=2 ,
所以 PC=22+(22)2+(22)2=25 ,
所以外接球半径为 5 ,
所以球O的体积 V=4π×(5)2=20π 。
故答案为:D.
4.【答案】 D
【解析】过 D 作 DD1⊥BC 交 BC 于 D1 ,
因为三棱柱侧棱垂直底面,所以 BB1⊥ 面 ABC , DD1? 面 ABC ,
所以 BB1⊥DD1 ,
又 BB1∩BC=B , BB1,BC? 面 BB1C1C ,
所以 DD1⊥ 面 BB1C1C , EF? 面 BB1C1C ,所以 DD1⊥EF ,
过 D 作 DD2⊥EF 交 EF 于 D2 ,连接 D1D2 ,
DD1∩DD2=D , DD1,DD2? 平面 DD1D2 ,
所以 EF⊥ 平面 DD1D2 ,又 D1D2? 平面 DD1D2 ,
所以 EF⊥D1D2 ,所以 ∠D1D2D 是二面角 D?EF?B 的平面角,即 ∠D1D2D =α ,
由 DD1⊥ 面 BB1C1C , D1D2? 面 BB1C1C ,得 DD1⊥D1D2 ,
因为 ∠BAC=90° , AB=AC=22AA1 ,所以 BC=AA1=BB1 ,
即 BB1C1C 是正方形,
D 是 AB 中点,则 D1 是 BC 的四等分点.
设 BC=4 ,则 DD1=BD1=1 ,
在平面 B1BCC1 上以 B1C1 , B1B 为 x,y 轴建立平面直角坐标系,
如图,则 D1(1,4) , E(2,0) ,设 F(4,t) , 0≤t≤4 ,
kEF=t2 ,直线 EF 的方程为 y=t2(x?2) ,即 tx?2y?2t=0 ,
D1 到直线 EF 的距离为 D1D2=|t?8?2t|t2+4=t+8t2+4 ,
tanα=DD1D1D2=t2+4t+8 ,
设 f(t)=t2+4(t+8)2 ,则 f′(t)=8(2t?1)(t+8)3 ,
当 0≤t<12 时, f′(t)<0 , f(t) 递减,当 120 , f(t) 递增.
所以 tanα 先减后增,而 α 为锐角,所以 α 先减后增.
故答案为:D.
5.【答案】 3;4
【解析】解:两个平行平面将空间分成3部分,两个相交平面可以将空间分成4部分,
故答案为:3;4。
6.【答案】 2+3
【解析】球 O1 的半径为1,设球 O2 的半径为r,
则有 (1+r)2?(1?r)2=(2?2r)2 ,
解得 r=2?3 ,所以球 O1 与球 O2 的半径之比为 12?3=2+3 。
故答案为: 2+3。
【8.1基本立体图形】
【学习目标】掌握立体图形的结构特征
【难点突破】
知识点1:棱柱的结构特征
一般地,有两个面互相平行,其余各面都是四边形,并且相邻两个四边形的公共边都互侧相平行,由这些面所围成的几何体叫做棱柱.
知识点2:棱锥的结构 一般地,有一个面是多边形,其余各面都是有一个公共顶点的三角形,由这些面所围成的几何体叫做棱锥
知识点3:棱台于圆台的结构特征
用一个平行于棱锥底面的平面去截棱锥,底面和截面之间那部分,这样的几何体叫做棱台
【例题分析】
例1.已知正方体 ABCD?A1B1C1D1 的棱长为2, AB , AD 中点分别为 E , F ,若过 EF 的平面截该正方体所得的截面是一个五边形,则该五边形周长的最大值为(??? )
A.?2+213????????????????????????B.?2+13????????????????????????C.?32+25????????????????????????D.?32+5
【答案】 A
【解析】将面 BCC1B1 展开与面 ABB1A1 处于同一平面要使 EQ+QC1+FH+HCl 最大,则沿面 C1QEFH 切才能保证五点共面,在 Rt△ECC1 中, CC1=BC=2,BE=12AB=1 ,此时 EQ+QC1=22+(2+1)2=13 ,又 FH+HC1=EQ+QC=13 ,
∴ 该五边形周长的最大值为 EF+2(EQ+QC1)=2+213。
故答案为:A
例2.在正方体 ABCD?A1B1C1D1 中,过点 C 做直线 l ,使得直线 l 与直线 BA1 和 B1D1 所成的角均为 70o ,则这样的直线 l (??? )
A.?不存在???????????????????????????????????B.?2条???????????????????????????????????C.?4条???????????????????????????????????D.?无数条
【答案】 C
【解析】因为 B1D1//BD ,过点 C 做直线 l 可以转化为过 B 做直线 l 与直线 BA1 和 BD 所成的角均为 70o ,由于 BA1 与 BD 所成的角都等于 60o ,所以当直线 l 是 ∠A1BD 的角平分线时与 A1B、BD 都成 30o ,然后直线 l 绕着点B转动,在与平面 A1BD 垂直的过程中有一条直线与两条直线都成 70o ,同理在 ∠A1BD 的对顶角中也有一条直线 l 与两条直线都成 70o ,
因为 ∠A1BD 的补角是 120o ,角平分线与两条直线都成 60o ,当直线 l 绕着点B从 ∠A1BD 一侧的补角角平分线开始转动,在与平面 A1BD 垂直的过程中有一条直线与两条直线都成 70o ,同理另一侧的补角也存在一条,所以共有4条.
故答案为:C.
【小题演练】
1.如图,正方体 ABCD?A1B1C1D1 中, AP=2PA1 ,点 M 在侧面 AA1B1B 内.若 D1M⊥CP ,则点 M 的轨迹为(?? ?)
A.?线段?????????????????????????????B.?圆弧?????????????????????????????C.?抛物线一部分?????????????????????????????D.?椭圆一部分
2.已知正三棱柱 ABC?A1B1C1 ,的体积为 163 ,底面积为 43 ,则三棱柱 ABC?A1B1C1 的外接球表面积为(??? )
A.?1123π???????????????????????????????????B.?563π???????????????????????????????????C.?2243π???????????????????????????????????D.?28π
3.在三棱锥 P?ABC 中, PA⊥ 平面 ABC , AP=2 , AB=22 , AC=4 , ∠BAC=45° ,则三棱锥 P?ABC 外接球的表面积是(??? )
A.?14π?????????????????????????????????????B.?16π?????????????????????????????????????C.?18π?????????????????????????????????????D.?20π
4.如图,在侧棱垂直底面的三棱柱 ABC?A1B1C1 中, ∠BAC=90° , AB=AC=22AA1 , D , E 分别是棱 AB , B1C1 的中点, F 是棱 CC1 上的一动点,记二面角 D?EF?B 的大小为 α ,则在 F 从 C1 运动到 C 的过程中, α 的变化情况为(??? )
A.?增大???????????????????????????B.?减小???????????????????????????C.?先增大再减小???????????????????????????D.?先减小再增大
5.在空间中,两个不同平面把空间最少可分成________部分,最多可分成________部分.
6.已知球 O1 是棱长为2的正方体 ABCD?A1B1C1D1 的内切球,球 O2 (在正方体 ABCD?A1B1C1D1 内部)与平面 ABCD ,平面 ABB1A1 和平面 ADD1A1 都相切,并且与球 O1 相切,则球 O1 与球 O2 的半径之比为________.
【参考答案】
1.【答案】 A
【解析】如图建立空间直角坐标系,
设棱长为3, P(3,0,2) , C(0,3,0) , D1(0,0,3) , M(3,y,z) , D1M=(3,y,z?3) , CP=(3,?3,2) ,
D1M?CP=9?3y+2(z?3)=0 ,整理为: 3y?2z?3=0 ,
所以点 M 的轨迹方程是关于 y,z 的二元一次方程,所以点M的轨迹是平面 ABB1A1 平面内,直线 3y?2z?3=0 内的一段线段。
故答案为:A
2.【答案】 A
【解析】依题意, AA1=16343=4 ,而 S△ABC=12AB×AC×sinA=34AB2=43 ,
解得 AB=4 ,记 △ABC 的中心为О, △A1B1C1 的中心为О1 , 则 AA1=OO1=4 ,
取 OO1 的中点 D ,因为 AO=CO , ∠AOD=∠COD=90? ,由勾股定理得 AD=CD ,
同理可得 AD=BD=A1D=B1D=C1D ,
所以正三棱柱的外接球的球心为即 D , AD 为外接球的半径,
由正弦定理得 AO=AB2sin60?=433 ,
故 AD2=OD2+AO2=4+163=283 ,
故三棱柱 ABC?A1B1C1 的外接球表面积 S=4πR2=4π×283=1123π ,
故答案为:A.
3.【答案】 D
【解析】在 △BAC 中, ∠BAC=45° , AB=22 , AC=4 ,
由余弦定理可得 BC2=AB2+AC2?2AB?ACcosπ4=8+16?2×4×22×22=22 ,
则 BC2+AB2=AC2 ,所以 BC⊥AB ,
由 PA⊥ 平面 ABC ,则 PA⊥BC , PA∩AB=A ,
所以 BC⊥ 平面 PAB ,
所以 BC⊥PB ,
所以 △PBC 为直角三角形,
又 △PAC 为直角三角形,
所以 PC 是外接球直径,O是 PC 的中点,即为球心,
又 AB=BC=22,?PA=2 ,
所以 PC=22+(22)2+(22)2=25 ,
所以外接球半径为 5 ,
所以球O的体积 V=4π×(5)2=20π 。
故答案为:D.
4.【答案】 D
【解析】过 D 作 DD1⊥BC 交 BC 于 D1 ,
因为三棱柱侧棱垂直底面,所以 BB1⊥ 面 ABC , DD1? 面 ABC ,
所以 BB1⊥DD1 ,
又 BB1∩BC=B , BB1,BC? 面 BB1C1C ,
所以 DD1⊥ 面 BB1C1C , EF? 面 BB1C1C ,所以 DD1⊥EF ,
过 D 作 DD2⊥EF 交 EF 于 D2 ,连接 D1D2 ,
DD1∩DD2=D , DD1,DD2? 平面 DD1D2 ,
所以 EF⊥ 平面 DD1D2 ,又 D1D2? 平面 DD1D2 ,
所以 EF⊥D1D2 ,所以 ∠D1D2D 是二面角 D?EF?B 的平面角,即 ∠D1D2D =α ,
由 DD1⊥ 面 BB1C1C , D1D2? 面 BB1C1C ,得 DD1⊥D1D2 ,
因为 ∠BAC=90° , AB=AC=22AA1 ,所以 BC=AA1=BB1 ,
即 BB1C1C 是正方形,
D 是 AB 中点,则 D1 是 BC 的四等分点.
设 BC=4 ,则 DD1=BD1=1 ,
在平面 B1BCC1 上以 B1C1 , B1B 为 x,y 轴建立平面直角坐标系,
如图,则 D1(1,4) , E(2,0) ,设 F(4,t) , 0≤t≤4 ,
kEF=t2 ,直线 EF 的方程为 y=t2(x?2) ,即 tx?2y?2t=0 ,
D1 到直线 EF 的距离为 D1D2=|t?8?2t|t2+4=t+8t2+4 ,
tanα=DD1D1D2=t2+4t+8 ,
设 f(t)=t2+4(t+8)2 ,则 f′(t)=8(2t?1)(t+8)3 ,
当 0≤t<12 时, f′(t)<0 , f(t) 递减,当 12
所以 tanα 先减后增,而 α 为锐角,所以 α 先减后增.
故答案为:D.
5.【答案】 3;4
【解析】解:两个平行平面将空间分成3部分,两个相交平面可以将空间分成4部分,
故答案为:3;4。
6.【答案】 2+3
【解析】球 O1 的半径为1,设球 O2 的半径为r,
则有 (1+r)2?(1?r)2=(2?2r)2 ,
解得 r=2?3 ,所以球 O1 与球 O2 的半径之比为 12?3=2+3 。
故答案为: 2+3。
同课章节目录
- 第六章 平面向量及其应用
- 6.1 平面向量的概念
- 6.2 平面向量的运算
- 6.3 平面向量基本定理及坐标表示
- 6.4 平面向量的应用
- 第七章 复数
- 7.1 复数的概念
- 7.2 复数的四则运算
- 7.3 * 复数的三角表示
- 第八章 立体几何初步
- 8.1 基本立体图形
- 8.2 立体图形的直观图
- 8.3 简单几何体的表面积与体积
- 8.4 空间点、直线、平面之间的位置关系
- 8.5 空间直线、平面的平行
- 8.6 空间直线、平面的垂直
- 第九章 统计
- 9.1 随机抽样
- 9.2 用样本估计总体
- 9.3 统计分析案例 公司员工
- 第十章 概率
- 10.1 随机事件与概率
- 10.2 事件的相互独立性
- 10.3 频率与概率
