8.6空间直线、平面之间的垂直-【新教材】2020-2021学年人教A版(2019)高中数学必修第二册同步讲义(含答案)
文档属性
| 名称 | 8.6空间直线、平面之间的垂直-【新教材】2020-2021学年人教A版(2019)高中数学必修第二册同步讲义(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 109.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-04-19 21:15:05 | ||
图片预览


文档简介
高一数学人教版(2019)必修第二册
【8.6空间直线、平面之间的垂直】
【学习目标】掌握空间直线、平面之间的垂直的判定定理和性质定理
【难点突破】
知识点1:点到平面的距离
(1)过一点垂直于已知平面的直线有且只有一条
(2)定义:过一点做垂直于已知平面的直线,则该点与垂足间的线段,叫做这个点到该平面的垂线段,垂线段的长度叫做这个点到该平面的距离
知识点2:直线与平面垂直性质定理
垂直于同一个平面的两条直线平行
false
知识点3:直线与平面所成的角
一条直线1与一个平面false相交,但不与这个平面垂直,这条直线叫做这个平面的斜线,斜线和平面的交点A叫做斜足.
过斜线上斜足以外的一点P向平面false引垂线 PO,过垂足O和斜足A的直线A0叫做斜线在这个平面上的射影.平面的一条斜线和它在平面上的射影所成的角,叫做这条直线和这个平面所成的角
【例题分析】
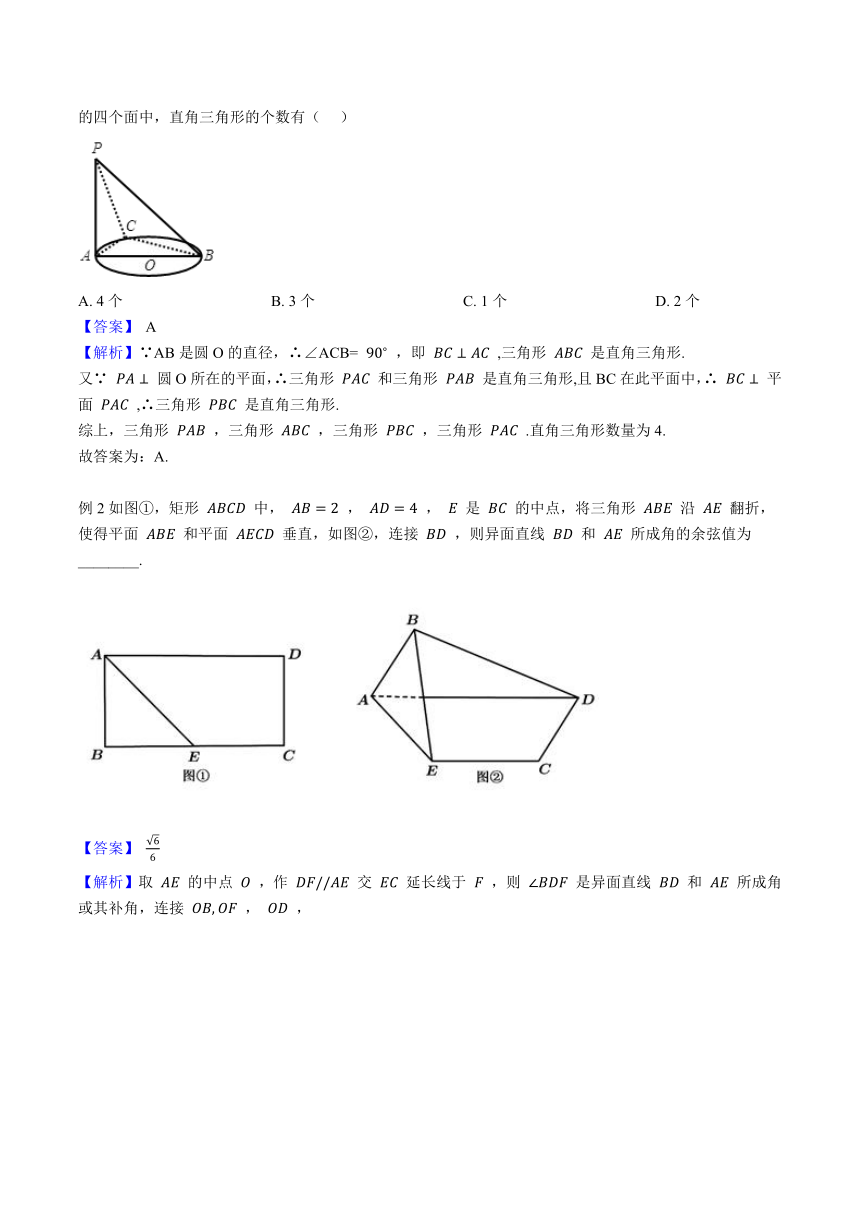
例1.如图,AB是⊙O直径,C是圆周上不同于A、B的任意一点,PA与平面ABC垂直,则四面体P_ABC的四个面中,直角三角形的个数有(??? )
A.?4个???????????????????????????????????????B.?3个???????????????????????????????????????C.?1个???????????????????????????????????????D.?2个
【答案】 A
【解析】∵AB是圆O的直径,∴∠ACB= 90? ,即 BC⊥AC ,三角形 ABC 是直角三角形.
又∵ PA⊥ 圆O所在的平面,∴三角形 PAC 和三角形 PAB 是直角三角形,且BC在此平面中,∴ BC⊥ 平面 PAC ,∴三角形 PBC 是直角三角形.
综上,三角形 PAB ,三角形 ABC ,三角形 PBC ,三角形 PAC .直角三角形数量为4.
故答案为:A.
例2如图①,矩形 ABCD 中, AB=2 , AD=4 , E 是 BC 的中点,将三角形 ABE 沿 AE 翻折,使得平面 ABE 和平面 AECD 垂直,如图②,连接 BD ,则异面直线 BD 和 AE 所成角的余弦值为________.
【答案】 66
【解析】取 AE 的中点 O ,作 DF//AE 交 EC 延长线于 F ,则 ∠BDF 是异面直线 BD 和 AE 所成角或其补角,连接 OB,OF , OD ,
∵ AB=BE ,所以 BO⊥AE ,
又平面 ABE ⊥ 平面 ECDA ,平面 ABE ∩ 平面 ECDA =AE , BO? 平面 ABE ,
∴ BO⊥ 平面 ECDA ,
而 OD,OF? 平面 ECDA ,所以 BO⊥OF , BO⊥OD ,
又∵ ∠ABE=90° , AB=BE=2 ,所以 BO=2 , AO=EO=2 , AE=22 ,
DF//AE , AD//EF ,则 ADFE 是平行四边形, EF=AD=4,DF=AE=22 ,
在原矩形中 ∠BAE=∠BEA=45° ,则 ∠DAE=45°,∠CEA=135° ,
OD=AD2+AO2?2AD?AOcos45°=42+2?2×4×2×22=10 ,
OF=EF2+EO2?2EF?EOcos135°=42+2+2×4×2×22=26 ,
BD2=BO2+OD2=12 , BF2=BO2+OF2=28 ,
在 △BDF 中, cos∠BDF=BD2+DF2?BF22BD?DF =12+8?282×12×22=?66 ,
所以异面直线 BD 和 AE 所成角的余弦为 66 .
故答案为: 66 .
【小题演练】
1.如图,在正方体 ABCD?A1B1C1D1 中, M , N 分别是 BC1 , CD1 的中点,则下列说法错误的是(??? )
A.?MN 与 CC1 垂直?????????B.?MN 与 AC 垂直?????????C.?MN 与 BD 平行?????????D.?MN 与 A1B1 平行
2.三棱锥 P?ABC 的各棱长都相等, D、E、F 分别是 AB、BC、CA 的中点,下列四个结论中不成立的是(??? )
A.?BC// 平面 PDF??????????????????????????????????????????????B.?DF⊥ 平面 PAE
C.?平面 PDE⊥ 平面 ABC???????????????????????????????????D.?平面 PAE⊥ 平面 ABC
3.在空间中,设 m、n 是不同的直线, α、β 表示不同的平面,则下列命题正确的是 (??? )
A.?若 α//β,m//α ,则 m//β????????????????????????????????????B.?若 α⊥β,m⊥α ,则 m//β
C.?若 α⊥β,m//α ,则 m⊥β???????????????????????????????D.?若 α⊥β,m⊥α,n⊥β ,则 m⊥n
4.设m,n是两条不同的直线, α,β 是两个不重合的平面,下列命题中正确的是(??? )
① m⊥nn?α}?m⊥α ?? ② m⊥αm?β}?α⊥β ?? ③ m⊥αn⊥α}?m//n ??? ④ m?αn?βα//β}?m//n
A.?①②?????????????????????????????????????B.?①④?????????????????????????????????????C.?②③?????????????????????????????????????D.?②④
5.如图,在侧棱垂直于底面的三棱柱 ABC?A1B1C1 中, AB⊥BC , AB=BC=CC1 , E ,F分别是 BC , B1C1 的中点,则异面直线 AF 与 C1E 所成角的余弦值是________.
6.已知 α,β 是空间两个不同的平面, m,n 是空间两条不同的直线,给出的下列说法:
①若 m//α,n//β ,且 m//n ,则 α//β ;
②若 m//α,n//β ,且 m⊥n ,则 α⊥β ;
③若 m⊥α,n⊥β ,且 m//n ,则 α//β ;
④若 m⊥α,n⊥β ,且 m⊥n ,则 α⊥β .
其中正确的说法为________(填序号)
【参考答案】
1.【答案】 D
【解析】如图:连接 C1D , BD ,
∵ 在三角形 C1DB 中, MN//BD ,C符合题意.
∵CC1⊥ 平面 ABCD , ∴CC1⊥BD , ∴MN 与 CC1 垂直,A符合题意;
∵AC⊥BD , MN//BD , ∴MN 与 AC 垂直,B符合题意;
∵ MN//BD , ∴MN 与 A1B1 不可能平行,D不符合题意
故答案为:D.
2.【答案】 C
【解析】对于A中,因为 D,F 分别是 AB,CA 的中点,可得 BC//DF ,
因为 BC? 平面 PDF , DF? 平面 PDF ,所以 BC// 平面 PDF ,所以A符合题意;
对于B中,因为 AC=AB,BE=EC ,所以 BC⊥AE ,
同理可得 BC⊥PE ,
又因为 PE∩AE=E ,所以 BC⊥ 平面 PAE ,
又由 BC//DE ,所以 DF⊥ 平面 PAE ,所以B符合题意;
对于D中,由 DF⊥ 平面 PAE ,因为 DF? 平面 ABC ,
所以平面 PAE⊥ 平面 ABC ,所以D符合题意;
综上可得A、B、D都正确,所以C不正确.
故答案为:C.
3.【答案】 D
【解析】对于A,若 α//β,m//α ,可得 m//β 或 m?β ,A不符合题意;
对于B,若 α⊥β,m⊥α ,可得 m?β 或 m//β ,B不符合题意;
对于C,若 α⊥β,m//α ,则 m?β ,或 m//β ,或 m 与 β 相交,C不符合题意;
对于D,若 α⊥β,m⊥α,n⊥β ,则 m⊥n ,正确.
故答案为:D.
4.【答案】 C
【解析】对①,若 m⊥n,n?α ,则 m 和 α 可能相交,平行或在平面内,故①错误;
对②,若 m⊥α,m?β ,则由面面垂直的判定定理可得 α⊥β ,故②正确;
对③,若 m⊥α,n⊥α ,则由线面垂直的性质可得 m//n ,故③正确;
对④,若 m?α,n?β,α//β ,则 m 和 n 平行或异面,故④错误.
故答案为:C.
5.【答案】 53
【解析】连结BF,在三棱柱 ABC?A1B1C1 中,因为 E ,F分别是 BC , B1C1 的中点,
所以 BF ∥ C1E ,则∠AFB(或其补角)即为异面直线 AF 与 C1E 所成角.
在三棱柱 ABC?A1B1C1 中,因为侧棱垂直于底面,即 BB1⊥ABC ,所以 BB1⊥AB .
又 AB⊥BC ,且 BB1∩BC=B ,所以 AB⊥ 平面 BB1C1C ,而 BF? 平面平面 BB1C1C ,
所以 AB⊥BF
不妨设AB=2,
在直角三角形ABF中,AB=2, BF=1+22=5,AF=AB2+BF2=22+5=3
所以异面直线 AF 与 C1E 所成角的余弦值为: cosθ=53 .
故答案为: 53
6.【答案】 ③④
【解析】① m//α , n//β ,且 m//n ,则 α,β 可能相交,故①错误;
② m//α , n//β ,且 m⊥n ,则 α,β 可能相交,也可能平行,故②错误;
③ m⊥α , n⊥β ,且 m//n ,则 α//β ,根据线面垂直的性质可知③正确;
④ m⊥α , n⊥β 、且 m⊥n ,则 α⊥β ,根据线面垂直的性质可知④正确.
故答案为:③④.
【8.6空间直线、平面之间的垂直】
【学习目标】掌握空间直线、平面之间的垂直的判定定理和性质定理
【难点突破】
知识点1:点到平面的距离
(1)过一点垂直于已知平面的直线有且只有一条
(2)定义:过一点做垂直于已知平面的直线,则该点与垂足间的线段,叫做这个点到该平面的垂线段,垂线段的长度叫做这个点到该平面的距离
知识点2:直线与平面垂直性质定理
垂直于同一个平面的两条直线平行
false
知识点3:直线与平面所成的角
一条直线1与一个平面false相交,但不与这个平面垂直,这条直线叫做这个平面的斜线,斜线和平面的交点A叫做斜足.
过斜线上斜足以外的一点P向平面false引垂线 PO,过垂足O和斜足A的直线A0叫做斜线在这个平面上的射影.平面的一条斜线和它在平面上的射影所成的角,叫做这条直线和这个平面所成的角
【例题分析】
例1.如图,AB是⊙O直径,C是圆周上不同于A、B的任意一点,PA与平面ABC垂直,则四面体P_ABC的四个面中,直角三角形的个数有(??? )
A.?4个???????????????????????????????????????B.?3个???????????????????????????????????????C.?1个???????????????????????????????????????D.?2个
【答案】 A
【解析】∵AB是圆O的直径,∴∠ACB= 90? ,即 BC⊥AC ,三角形 ABC 是直角三角形.
又∵ PA⊥ 圆O所在的平面,∴三角形 PAC 和三角形 PAB 是直角三角形,且BC在此平面中,∴ BC⊥ 平面 PAC ,∴三角形 PBC 是直角三角形.
综上,三角形 PAB ,三角形 ABC ,三角形 PBC ,三角形 PAC .直角三角形数量为4.
故答案为:A.
例2如图①,矩形 ABCD 中, AB=2 , AD=4 , E 是 BC 的中点,将三角形 ABE 沿 AE 翻折,使得平面 ABE 和平面 AECD 垂直,如图②,连接 BD ,则异面直线 BD 和 AE 所成角的余弦值为________.
【答案】 66
【解析】取 AE 的中点 O ,作 DF//AE 交 EC 延长线于 F ,则 ∠BDF 是异面直线 BD 和 AE 所成角或其补角,连接 OB,OF , OD ,
∵ AB=BE ,所以 BO⊥AE ,
又平面 ABE ⊥ 平面 ECDA ,平面 ABE ∩ 平面 ECDA =AE , BO? 平面 ABE ,
∴ BO⊥ 平面 ECDA ,
而 OD,OF? 平面 ECDA ,所以 BO⊥OF , BO⊥OD ,
又∵ ∠ABE=90° , AB=BE=2 ,所以 BO=2 , AO=EO=2 , AE=22 ,
DF//AE , AD//EF ,则 ADFE 是平行四边形, EF=AD=4,DF=AE=22 ,
在原矩形中 ∠BAE=∠BEA=45° ,则 ∠DAE=45°,∠CEA=135° ,
OD=AD2+AO2?2AD?AOcos45°=42+2?2×4×2×22=10 ,
OF=EF2+EO2?2EF?EOcos135°=42+2+2×4×2×22=26 ,
BD2=BO2+OD2=12 , BF2=BO2+OF2=28 ,
在 △BDF 中, cos∠BDF=BD2+DF2?BF22BD?DF =12+8?282×12×22=?66 ,
所以异面直线 BD 和 AE 所成角的余弦为 66 .
故答案为: 66 .
【小题演练】
1.如图,在正方体 ABCD?A1B1C1D1 中, M , N 分别是 BC1 , CD1 的中点,则下列说法错误的是(??? )
A.?MN 与 CC1 垂直?????????B.?MN 与 AC 垂直?????????C.?MN 与 BD 平行?????????D.?MN 与 A1B1 平行
2.三棱锥 P?ABC 的各棱长都相等, D、E、F 分别是 AB、BC、CA 的中点,下列四个结论中不成立的是(??? )
A.?BC// 平面 PDF??????????????????????????????????????????????B.?DF⊥ 平面 PAE
C.?平面 PDE⊥ 平面 ABC???????????????????????????????????D.?平面 PAE⊥ 平面 ABC
3.在空间中,设 m、n 是不同的直线, α、β 表示不同的平面,则下列命题正确的是 (??? )
A.?若 α//β,m//α ,则 m//β????????????????????????????????????B.?若 α⊥β,m⊥α ,则 m//β
C.?若 α⊥β,m//α ,则 m⊥β???????????????????????????????D.?若 α⊥β,m⊥α,n⊥β ,则 m⊥n
4.设m,n是两条不同的直线, α,β 是两个不重合的平面,下列命题中正确的是(??? )
① m⊥nn?α}?m⊥α ?? ② m⊥αm?β}?α⊥β ?? ③ m⊥αn⊥α}?m//n ??? ④ m?αn?βα//β}?m//n
A.?①②?????????????????????????????????????B.?①④?????????????????????????????????????C.?②③?????????????????????????????????????D.?②④
5.如图,在侧棱垂直于底面的三棱柱 ABC?A1B1C1 中, AB⊥BC , AB=BC=CC1 , E ,F分别是 BC , B1C1 的中点,则异面直线 AF 与 C1E 所成角的余弦值是________.
6.已知 α,β 是空间两个不同的平面, m,n 是空间两条不同的直线,给出的下列说法:
①若 m//α,n//β ,且 m//n ,则 α//β ;
②若 m//α,n//β ,且 m⊥n ,则 α⊥β ;
③若 m⊥α,n⊥β ,且 m//n ,则 α//β ;
④若 m⊥α,n⊥β ,且 m⊥n ,则 α⊥β .
其中正确的说法为________(填序号)
【参考答案】
1.【答案】 D
【解析】如图:连接 C1D , BD ,
∵ 在三角形 C1DB 中, MN//BD ,C符合题意.
∵CC1⊥ 平面 ABCD , ∴CC1⊥BD , ∴MN 与 CC1 垂直,A符合题意;
∵AC⊥BD , MN//BD , ∴MN 与 AC 垂直,B符合题意;
∵ MN//BD , ∴MN 与 A1B1 不可能平行,D不符合题意
故答案为:D.
2.【答案】 C
【解析】对于A中,因为 D,F 分别是 AB,CA 的中点,可得 BC//DF ,
因为 BC? 平面 PDF , DF? 平面 PDF ,所以 BC// 平面 PDF ,所以A符合题意;
对于B中,因为 AC=AB,BE=EC ,所以 BC⊥AE ,
同理可得 BC⊥PE ,
又因为 PE∩AE=E ,所以 BC⊥ 平面 PAE ,
又由 BC//DE ,所以 DF⊥ 平面 PAE ,所以B符合题意;
对于D中,由 DF⊥ 平面 PAE ,因为 DF? 平面 ABC ,
所以平面 PAE⊥ 平面 ABC ,所以D符合题意;
综上可得A、B、D都正确,所以C不正确.
故答案为:C.
3.【答案】 D
【解析】对于A,若 α//β,m//α ,可得 m//β 或 m?β ,A不符合题意;
对于B,若 α⊥β,m⊥α ,可得 m?β 或 m//β ,B不符合题意;
对于C,若 α⊥β,m//α ,则 m?β ,或 m//β ,或 m 与 β 相交,C不符合题意;
对于D,若 α⊥β,m⊥α,n⊥β ,则 m⊥n ,正确.
故答案为:D.
4.【答案】 C
【解析】对①,若 m⊥n,n?α ,则 m 和 α 可能相交,平行或在平面内,故①错误;
对②,若 m⊥α,m?β ,则由面面垂直的判定定理可得 α⊥β ,故②正确;
对③,若 m⊥α,n⊥α ,则由线面垂直的性质可得 m//n ,故③正确;
对④,若 m?α,n?β,α//β ,则 m 和 n 平行或异面,故④错误.
故答案为:C.
5.【答案】 53
【解析】连结BF,在三棱柱 ABC?A1B1C1 中,因为 E ,F分别是 BC , B1C1 的中点,
所以 BF ∥ C1E ,则∠AFB(或其补角)即为异面直线 AF 与 C1E 所成角.
在三棱柱 ABC?A1B1C1 中,因为侧棱垂直于底面,即 BB1⊥ABC ,所以 BB1⊥AB .
又 AB⊥BC ,且 BB1∩BC=B ,所以 AB⊥ 平面 BB1C1C ,而 BF? 平面平面 BB1C1C ,
所以 AB⊥BF
不妨设AB=2,
在直角三角形ABF中,AB=2, BF=1+22=5,AF=AB2+BF2=22+5=3
所以异面直线 AF 与 C1E 所成角的余弦值为: cosθ=53 .
故答案为: 53
6.【答案】 ③④
【解析】① m//α , n//β ,且 m//n ,则 α,β 可能相交,故①错误;
② m//α , n//β ,且 m⊥n ,则 α,β 可能相交,也可能平行,故②错误;
③ m⊥α , n⊥β ,且 m//n ,则 α//β ,根据线面垂直的性质可知③正确;
④ m⊥α , n⊥β 、且 m⊥n ,则 α⊥β ,根据线面垂直的性质可知④正确.
故答案为:③④.
同课章节目录
- 第六章 平面向量及其应用
- 6.1 平面向量的概念
- 6.2 平面向量的运算
- 6.3 平面向量基本定理及坐标表示
- 6.4 平面向量的应用
- 第七章 复数
- 7.1 复数的概念
- 7.2 复数的四则运算
- 7.3 * 复数的三角表示
- 第八章 立体几何初步
- 8.1 基本立体图形
- 8.2 立体图形的直观图
- 8.3 简单几何体的表面积与体积
- 8.4 空间点、直线、平面之间的位置关系
- 8.5 空间直线、平面的平行
- 8.6 空间直线、平面的垂直
- 第九章 统计
- 9.1 随机抽样
- 9.2 用样本估计总体
- 9.3 统计分析案例 公司员工
- 第十章 概率
- 10.1 随机事件与概率
- 10.2 事件的相互独立性
- 10.3 频率与概率
