8.5空间直线、平面之间的平行-【新教材】2020-2021学年人教A版(2019)高中数学必修第二册同步讲义(含答案)
文档属性
| 名称 | 8.5空间直线、平面之间的平行-【新教材】2020-2021学年人教A版(2019)高中数学必修第二册同步讲义(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 70.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-04-19 00:00:00 | ||
图片预览

文档简介
高一数学人教版(2019)必修第二册
【8.5空间直线、平面之间的平行】
【学习目标】掌握空间直线、平面之间的垂直定理及其符号语言认识
【难点突破】
知识点1:直线与直线平行
平行于同一条直线的两条直线平行
定理:如果空间中两个角的两条边分别对应平行,那么这两个角相等或互补
知识点2: 直线与平面平行
判定定理:如果平面外一条直线与此平面内的一条直线平行,那么该直线与此平面平行
符号语言:false
性质定理:一条直线与一个平面平行,如果过该直线的平面与此平面相交,那么该直线与交线平行
符号语言:false
知识点3:平面与平面平行
判定定理:如果一个平面内的两条相交直线与另一个平面平行,那么这两个平面平行
符号语言:false
性质定理:两个平面平行,如果另一个平面与这两个平面相交,那么两条交线平行
符号语言:false
【例题分析】
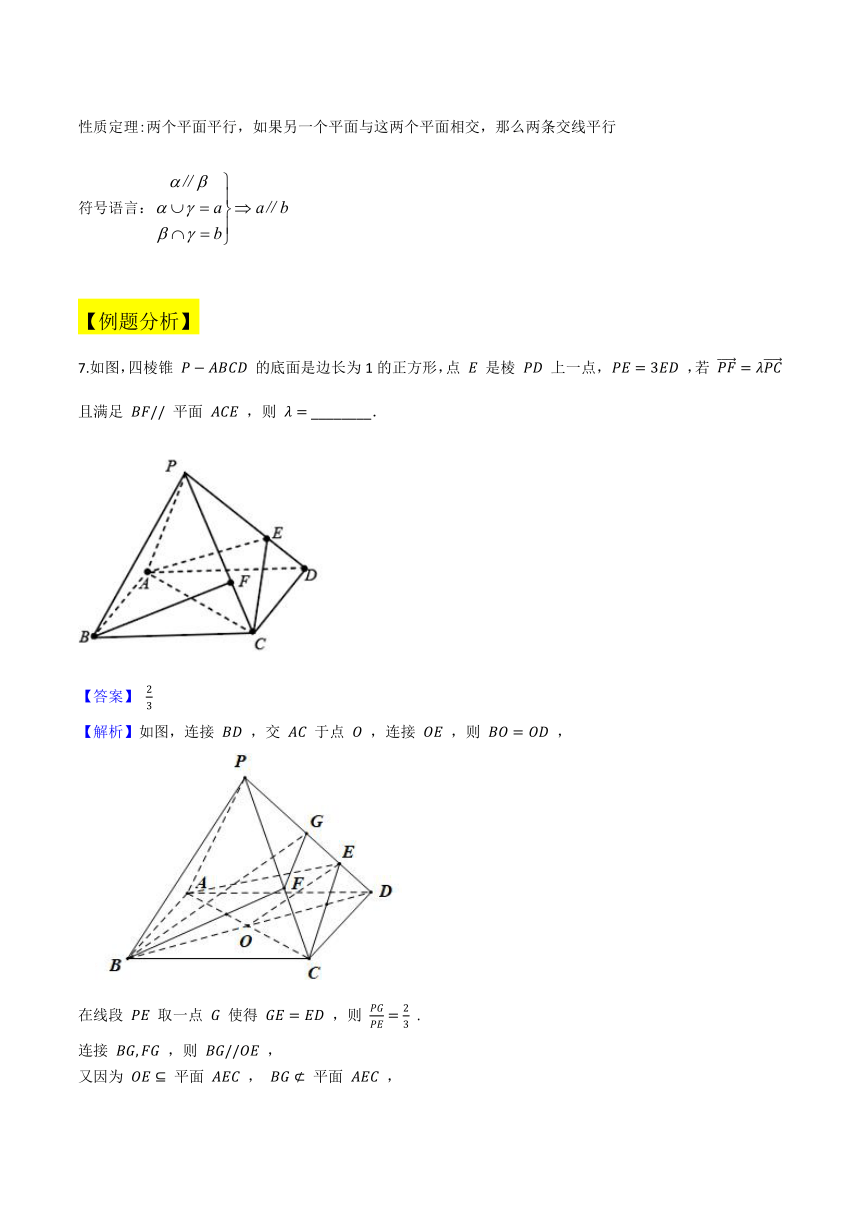
7.如图,四棱锥 P?ABCD 的底面是边长为1的正方形,点 E 是棱 PD 上一点, PE=3ED ,若 PF=λPC 且满足 BF// 平面 ACE ,则 λ= ________.
【答案】 23
【解析】如图,连接 BD ,交 AC 于点 O ,连接 OE ,则 BO=OD ,
在线段 PE 取一点 G 使得 GE=ED ,则 PGPE=23 .
连接 BG,FG ,则 BG//OE ,
又因为 OE? 平面 AEC , BG? 平面 AEC ,
所以 BG// 平面 AEC .
因为 BF// 平面 ACE 且满足 BG∩BF=B ,故平面 BGF// 平面 AEC .
因为平面 PCD∩ 平面 BGF=GF ,平面 PCD∩ 平面 AEC=EC ,则 GF//EC .
所以 PFPC=PGPE=23 ,即 λ=23 为所求.
故答案为: 23 .
在棱长为 1 的正方体 ABCD?A1B1C1D1 中,点 P1,P2 分别是线段 AB,BD1 (不包括端点)上的动点,且线段 P1P2 平行于平面 A1ADD1 ,则四面体 P1P2AB1 的体积的最大值是________.
【答案】 124
【解析】由线面平行的性质定理知 P1P2//AD1 , ∴△P1P2B ∽ △AD1B , P1BAB=P1P2AD1=P2BBD1 ,
设 P1B=x,x∈(0,1) ,则 P1P2=2x , P2 到平面 AA1B1B 的距离为 ? ,则 ?A1D1=P2BBD1 ,
所以 ?=x ,所以四面体 P1P2AB1 的体积为 V=13×12×(1?x)×1×x=16(x?x2)=?16(x?12)2+124 ,
当 x=12 时,四面体 P1P2AB1 的体积取得最大值: 124 .
所以答案应填: 124 .
【小题演练】
1.设 l,?m 是两条不同的直线, α 是一个平面,则下列说法正确的是(??? )
A.?若 l//α , m?α ,则 l//m????????????????????????????B.?若 l//α , m//α ,则 l//m
C.?若 l⊥m , m?α ,则 l⊥α????????????????????????????D.?若 l⊥α , l//m ,则 m⊥α
2.如图所示,在正方体 ABCD?A1B1C1D1 中, O 是底面正方形 ABCD 的中心, M 是 D1D 的中点, N 是 A1B1 的中点,则直线 NO , AM 的位置关系是(??? )
A.?平行???????????????????????????????B.?相交???????????????????????????????C.?异面垂直???????????????????????????????D.?异面不垂直
3.如果直线l的方向向量是 a=(?2,0,1) ,且直线l上有一点P不在平面 α 内,平面 α 的法向量是 b=(2,0,4) ,那么(??? ).
A.?直线l与平面 α 垂直
B.?直线l与平面 α 平行
C.?直线l在平面 α 内
D.?直线l与平面 α 相交但不垂直
4.在空间直角坐标系中,已知 A(1,2,3) , , C(3,2,1) , D(4,3,0) ,则直线 AB 与 CD 的位置关系是(???? )
A.?垂直????????????????????????????????B.?平行????????????????????????????????C.?异面????????????????????????????????D.?相交但不垂直
5.已知 △ABC 在平面 α 内, ∠A=90° , DA⊥ 平面 α ,则直线 CA 与 DB 的位置关系是________.
6.已知点 P 是平行四边形 ABCD 所在平面外一点,如果 AB=(2,?1,?4),AD=(4,2,0), AP=(?1,2,?1) ,对于结论:① AP⊥AB ;② AP⊥AD ;③ AP 是平面 ABCD 的法向量;④ AP//BD .其中正确的说法的序号是________.
【参考答案】
1.【答案】 D
【解析】已知 l,?m 是两条不同的直线, α 是一个平面,
A选项,若 l//α , m?α ,则 l 与 m 可能异面或平行,A不符合题意;
B选项,若 l//α , m//α ,则 l 与 m 可能异面、平行或相交,B不符合题意;
C选项,若 l⊥m , m?α ,则 l 与 α 可能平行、相交或线在面内,C不符合题意;
D选项,若 l⊥α ,则 l 垂直平面 α 内的任意一条直线;又 l//m ,则 m 也垂直平面 α 内的任意一条直线,所以 m⊥α ,D符合题意.
故答案为:D.
2.【答案】 C
【解析】建立空间直角坐标系,如图所示.设正方体的棱长为2,
则 A(2,0,0) , M(0,0,1) , O(1,1,0) , N(2,1,2) ,
∴ NO=(?1,0,?2) , AM=(?2,0,1) .
∵ NO?AM=0 ,
∴直线 NO , AM 的位置关系是异面垂直.
故答案为:C
3.【答案】 B
【解析】因为直线l的方向向量是 a=(?2,0,1) ,平面 α 的法向量是 b=(2,0,4) ,
又因为 a?b=?4+0+4=0 ,所以直线l在平面 α 内或与平面 α 平行,又因为直线l上有一点P不在平面 α 内,所以直线l与平面 α 平行.
故答案为:B
4.【答案】 B
【解析】因为 A(1,2,3) , B(?2,?1,6) , C(3,2,1) , D(4,3,0) ,所以, AB=(?3,?3,3),CD=(1,1,?1) ,可得 AB=?3CD ,所以 AB∥CD ,线 AB 与 CD 的位置关系是平行,故答案为:B.
5.【答案】 垂直
【解析】 ∵DA⊥ 平面 α , AC? 平面 α , ∴DA⊥CA ,
在 △ABC 中, ∵∠A=90° , ∴AB⊥CA ,
且 DA∩BA=A ,
∴CA⊥ 平面 DAB , DB? 平面 DAB ,
∴CA⊥DB 。
故答案为:垂直.
6.【答案】 ①②③
【解析】由 AB=(2,?1,?4),AD=(4,2,0),AP=(?1,2,?1) ,
在①中, AP?AB=?2?2+4=0 ,所以 AP⊥AB ,所以 AP⊥AB ,所以是正确的;
在②中, AP?AD=?4+4+0=0 ,所以 AP⊥AD ,所以 AP⊥AD ,所以是正确的;
在③中,由于 AP⊥AB , AP⊥AD ,且 AB∩AD=A ,可知 AP 是平面 ABCD 的法向量,所以是正确的;
在④中, BD=AD?AB=(2,3,4) ,
假设存在实数 λ 使得 AP=λBD ,则 {?1=2λ2=3λ?1=4λ ,此时无解,所以是不正确的,
所以正确命题的序号为①②③。
【8.5空间直线、平面之间的平行】
【学习目标】掌握空间直线、平面之间的垂直定理及其符号语言认识
【难点突破】
知识点1:直线与直线平行
平行于同一条直线的两条直线平行
定理:如果空间中两个角的两条边分别对应平行,那么这两个角相等或互补
知识点2: 直线与平面平行
判定定理:如果平面外一条直线与此平面内的一条直线平行,那么该直线与此平面平行
符号语言:false
性质定理:一条直线与一个平面平行,如果过该直线的平面与此平面相交,那么该直线与交线平行
符号语言:false
知识点3:平面与平面平行
判定定理:如果一个平面内的两条相交直线与另一个平面平行,那么这两个平面平行
符号语言:false
性质定理:两个平面平行,如果另一个平面与这两个平面相交,那么两条交线平行
符号语言:false
【例题分析】
7.如图,四棱锥 P?ABCD 的底面是边长为1的正方形,点 E 是棱 PD 上一点, PE=3ED ,若 PF=λPC 且满足 BF// 平面 ACE ,则 λ= ________.
【答案】 23
【解析】如图,连接 BD ,交 AC 于点 O ,连接 OE ,则 BO=OD ,
在线段 PE 取一点 G 使得 GE=ED ,则 PGPE=23 .
连接 BG,FG ,则 BG//OE ,
又因为 OE? 平面 AEC , BG? 平面 AEC ,
所以 BG// 平面 AEC .
因为 BF// 平面 ACE 且满足 BG∩BF=B ,故平面 BGF// 平面 AEC .
因为平面 PCD∩ 平面 BGF=GF ,平面 PCD∩ 平面 AEC=EC ,则 GF//EC .
所以 PFPC=PGPE=23 ,即 λ=23 为所求.
故答案为: 23 .
在棱长为 1 的正方体 ABCD?A1B1C1D1 中,点 P1,P2 分别是线段 AB,BD1 (不包括端点)上的动点,且线段 P1P2 平行于平面 A1ADD1 ,则四面体 P1P2AB1 的体积的最大值是________.
【答案】 124
【解析】由线面平行的性质定理知 P1P2//AD1 , ∴△P1P2B ∽ △AD1B , P1BAB=P1P2AD1=P2BBD1 ,
设 P1B=x,x∈(0,1) ,则 P1P2=2x , P2 到平面 AA1B1B 的距离为 ? ,则 ?A1D1=P2BBD1 ,
所以 ?=x ,所以四面体 P1P2AB1 的体积为 V=13×12×(1?x)×1×x=16(x?x2)=?16(x?12)2+124 ,
当 x=12 时,四面体 P1P2AB1 的体积取得最大值: 124 .
所以答案应填: 124 .
【小题演练】
1.设 l,?m 是两条不同的直线, α 是一个平面,则下列说法正确的是(??? )
A.?若 l//α , m?α ,则 l//m????????????????????????????B.?若 l//α , m//α ,则 l//m
C.?若 l⊥m , m?α ,则 l⊥α????????????????????????????D.?若 l⊥α , l//m ,则 m⊥α
2.如图所示,在正方体 ABCD?A1B1C1D1 中, O 是底面正方形 ABCD 的中心, M 是 D1D 的中点, N 是 A1B1 的中点,则直线 NO , AM 的位置关系是(??? )
A.?平行???????????????????????????????B.?相交???????????????????????????????C.?异面垂直???????????????????????????????D.?异面不垂直
3.如果直线l的方向向量是 a=(?2,0,1) ,且直线l上有一点P不在平面 α 内,平面 α 的法向量是 b=(2,0,4) ,那么(??? ).
A.?直线l与平面 α 垂直
B.?直线l与平面 α 平行
C.?直线l在平面 α 内
D.?直线l与平面 α 相交但不垂直
4.在空间直角坐标系中,已知 A(1,2,3) , , C(3,2,1) , D(4,3,0) ,则直线 AB 与 CD 的位置关系是(???? )
A.?垂直????????????????????????????????B.?平行????????????????????????????????C.?异面????????????????????????????????D.?相交但不垂直
5.已知 △ABC 在平面 α 内, ∠A=90° , DA⊥ 平面 α ,则直线 CA 与 DB 的位置关系是________.
6.已知点 P 是平行四边形 ABCD 所在平面外一点,如果 AB=(2,?1,?4),AD=(4,2,0), AP=(?1,2,?1) ,对于结论:① AP⊥AB ;② AP⊥AD ;③ AP 是平面 ABCD 的法向量;④ AP//BD .其中正确的说法的序号是________.
【参考答案】
1.【答案】 D
【解析】已知 l,?m 是两条不同的直线, α 是一个平面,
A选项,若 l//α , m?α ,则 l 与 m 可能异面或平行,A不符合题意;
B选项,若 l//α , m//α ,则 l 与 m 可能异面、平行或相交,B不符合题意;
C选项,若 l⊥m , m?α ,则 l 与 α 可能平行、相交或线在面内,C不符合题意;
D选项,若 l⊥α ,则 l 垂直平面 α 内的任意一条直线;又 l//m ,则 m 也垂直平面 α 内的任意一条直线,所以 m⊥α ,D符合题意.
故答案为:D.
2.【答案】 C
【解析】建立空间直角坐标系,如图所示.设正方体的棱长为2,
则 A(2,0,0) , M(0,0,1) , O(1,1,0) , N(2,1,2) ,
∴ NO=(?1,0,?2) , AM=(?2,0,1) .
∵ NO?AM=0 ,
∴直线 NO , AM 的位置关系是异面垂直.
故答案为:C
3.【答案】 B
【解析】因为直线l的方向向量是 a=(?2,0,1) ,平面 α 的法向量是 b=(2,0,4) ,
又因为 a?b=?4+0+4=0 ,所以直线l在平面 α 内或与平面 α 平行,又因为直线l上有一点P不在平面 α 内,所以直线l与平面 α 平行.
故答案为:B
4.【答案】 B
【解析】因为 A(1,2,3) , B(?2,?1,6) , C(3,2,1) , D(4,3,0) ,所以, AB=(?3,?3,3),CD=(1,1,?1) ,可得 AB=?3CD ,所以 AB∥CD ,线 AB 与 CD 的位置关系是平行,故答案为:B.
5.【答案】 垂直
【解析】 ∵DA⊥ 平面 α , AC? 平面 α , ∴DA⊥CA ,
在 △ABC 中, ∵∠A=90° , ∴AB⊥CA ,
且 DA∩BA=A ,
∴CA⊥ 平面 DAB , DB? 平面 DAB ,
∴CA⊥DB 。
故答案为:垂直.
6.【答案】 ①②③
【解析】由 AB=(2,?1,?4),AD=(4,2,0),AP=(?1,2,?1) ,
在①中, AP?AB=?2?2+4=0 ,所以 AP⊥AB ,所以 AP⊥AB ,所以是正确的;
在②中, AP?AD=?4+4+0=0 ,所以 AP⊥AD ,所以 AP⊥AD ,所以是正确的;
在③中,由于 AP⊥AB , AP⊥AD ,且 AB∩AD=A ,可知 AP 是平面 ABCD 的法向量,所以是正确的;
在④中, BD=AD?AB=(2,3,4) ,
假设存在实数 λ 使得 AP=λBD ,则 {?1=2λ2=3λ?1=4λ ,此时无解,所以是不正确的,
所以正确命题的序号为①②③。
同课章节目录
- 第六章 平面向量及其应用
- 6.1 平面向量的概念
- 6.2 平面向量的运算
- 6.3 平面向量基本定理及坐标表示
- 6.4 平面向量的应用
- 第七章 复数
- 7.1 复数的概念
- 7.2 复数的四则运算
- 7.3 * 复数的三角表示
- 第八章 立体几何初步
- 8.1 基本立体图形
- 8.2 立体图形的直观图
- 8.3 简单几何体的表面积与体积
- 8.4 空间点、直线、平面之间的位置关系
- 8.5 空间直线、平面的平行
- 8.6 空间直线、平面的垂直
- 第九章 统计
- 9.1 随机抽样
- 9.2 用样本估计总体
- 9.3 统计分析案例 公司员工
- 第十章 概率
- 10.1 随机事件与概率
- 10.2 事件的相互独立性
- 10.3 频率与概率
