3.1回归分析的基本思想及其初步应用-2020-2021学年人教A版高中数学选修2-3同步课时练(Word含解析)
文档属性
| 名称 | 3.1回归分析的基本思想及其初步应用-2020-2021学年人教A版高中数学选修2-3同步课时练(Word含解析) |

|
|
| 格式 | doc | ||
| 文件大小 | 201.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-04-19 00:00:00 | ||
图片预览

文档简介
高二年级(数学)学科习题卷
回归分析的基本思想及其初步应用
编号:111
一、选择题:
1.在对两个变量x,y进行线性回归分析时,有下列步骤:
①对所求出的回归直线方程作出解释;②收集数据(xi,yi),i=1,2,…,n;
③求线性回归方程; ④求相关系数; ⑤根据所搜集的数据绘制散点图.
如果根据可行性要求能够作出变量x,y具有线性相关的结论,
则在下列操作顺序中正确的是( )
A.①②⑤③④ B.③②④⑤①
C.②④③①⑤ D.②⑤④③①
2.有下列说法:
①在残差图中,残差点比较均匀地落在水平的带状区域内,说明选用的模型比较合适;
②R2来刻画回归的效果,R2值越大,说明模型的拟合效果越好;
③比较两个模型的拟合效果, 可以比较残差平方和的大小,残差平方和越小的模型,
拟合效果越好.
其中正确命题的个数是( )
A.0 B.1 C.2 D.3
3.下图是根据变量x,y的观测数据(xi,yi)(i=1,2,…,10)得到的散点图,由这些散点图可以判断变量x,y具有相关关系的图是( )
A.①② B.①④ C.②③ D.③④
4.已知变量x与y正相关,且由观测数据算得样本平均数=3,=3.5,则由该观测数据算得的线性回归方程可能为( )
A.=0.4x+2.3 B.=2x-2.4
C.=-2x+9.5 D.=-0.3x+4.4
5.某咖啡厅为了了解热饮的销售量y(个)与气温x(℃)之间的关系,随机统计了某4天的销售量与气温,并制作了对照表:
气温(℃) 18 13 10 -1
销售量(个) 24 34 38 64
由表中数据,得线性回归方程=-2x+a.当气温为-4 ℃时,预测销售量约为( )
A.68 B.66 C.72 D.70
6.为了解某社区居民的家庭年收入与年支出的关系,随机调查了该社区5户家庭,得到如下统计数据表:
收入x(万元) 8.2 8.6 10.0 11.3 11.9
支出y(万元) 6.2 7.5 8.0 8.5 9.8
根据上表可得回归直线方程=x+,其中=0.76,=-.据此估计,该社区一户年收入为15万元家庭的年支出为( )
A.11.4万元 B.11.8万元 C.12.0万元 D.12.2万元
7.在建立两个变量y与x的回归模型中,分别选择4个不同模型,求出它们相对应的R2如表,则其中拟合效果最好的模型是( )
模型 1 2 3 4
R2 0.67 0.85 0.49 0.23
A.模型1 B.模型2 C.模型3 D.模型4
8.如果某地的财政收入x与支出y满足线性回归方程y=bx+a+e(单位:亿元),其中b=0.8,
a=2,|e|≤0.5,如果今年该地区财政收入为10亿元,则年支出预计不会超过( )
A.10亿 B.9亿 C.10.5亿 D.9.5亿
9.为了解儿子身高与其父亲身高的关系,随机抽取5对父子的身高数据如下:
父亲身高x(cm) 174 176 176 176 178
儿子身高y(cm) 175 175 176 177 177
则y对x的线性回归方程为( ).
A.y=x-1 B.y=x+1 C.y=88+x D.y=176
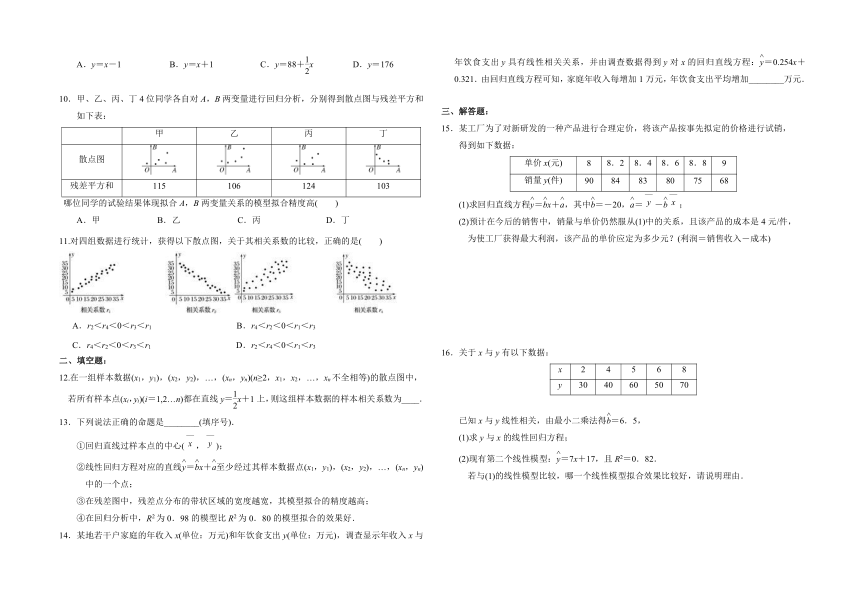
10.甲、乙、丙、丁4位同学各自对A,B两变量进行回归分析,分别得到散点图与残差平方和
如下表:
甲 乙 丙 丁
散点图
残差平方和 115 106 124 103
哪位同学的试验结果体现拟合A,B两变量关系的模型拟合精度高( )
A.甲 B.乙 C.丙 D.丁
11.对四组数据进行统计,获得以下散点图,关于其相关系数的比较,正确的是( )
A.r2<r4<0<r3<r1 B.r4<r2<0<r1<r3
C.r4<r2<0<r3<r1 D.r2<r4<0<r1<r3
二、填空题:
12.在一组样本数据(x1,y1),(x2,y2),…,(xn,yn)(n≥2,x1,x2,…,xn不全相等)的散点图中,
若所有样本点(xi,yi)(i=1,2…n)都在直线y=x+1上,则这组样本数据的样本相关系数为____.
13.下列说法正确的命题是________(填序号).
①回归直线过样本点的中心(,);
②线性回归方程对应的直线=x+至少经过其样本数据点(x1,y1),(x2,y2),…,(xn,yn)中的一个点;
③在残差图中,残差点分布的带状区域的宽度越宽,其模型拟合的精度越高;
④在回归分析中,R2为0.98的模型比R2为0.80的模型拟合的效果好.
14.某地若干户家庭的年收入x(单位:万元)和年饮食支出y(单位:万元),调查显示年收入x与年饮食支出y具有线性相关关系,并由调查数据得到y对x的回归直线方程:=0.254x+0.321.由回归直线方程可知,家庭年收入每增加1万元,年饮食支出平均增加________万元.
三、解答题:
15.某工厂为了对新研发的一种产品进行合理定价,将该产品按事先拟定的价格进行试销,
得到如下数据:
单价x(元) 8 8.2 8.4 8.6 8.8 9
销量y(件) 90 84 83 80 75 68
(1)求回归直线方程=x+,其中=-20,=-;
(2)预计在今后的销售中,销量与单价仍然服从(1)中的关系,且该产品的成本是4元/件,
为使工厂获得最大利润,该产品的单价应定为多少元?(利润=销售收入-成本)
16.关于x与y有以下数据:
x 2 4 5 6 8
y 30 40 60 50 70
已知x与y线性相关,由最小二乘法得=6.5,
(1)求y与x的线性回归方程;
(2)现有第二个线性模型:=7x+17,且R2=0.82.
若与(1)的线性模型比较,哪一个线性模型拟合效果比较好,请说明理由.
1、解析:选D 对两个变量进行回归分析时,首先收集数据(xi,yi),i=1,2,…,n;根据所搜集的数据绘制散点图.观察散点图的形状,判断线性相关关系的强弱,求相关系数,写出线性回归方程,最后依据所求出的回归直线方程作出解释;故正确顺序是②⑤④③①, 故选D.
2、解析:选D ①选用的模型是否合适与残差点的分布有关; 对于②③, R2的值越大, 说明残差平方和越小, 随机误差越小,则模型的拟合效果越好.
3、解析:选D 根据散点图中点的分布情况,可判断③④中的变量x,y具有相关的关系.
4、解析:选A 依题意知,相应的回归直线的斜率应为正,排除C,D.且直线必过点(3,3.5)代入A,B得A正确.
5、解析:选A ∵=(18+13+10-1)=10,=(24+34+38+64)=40,
∴40=-2×10+a,∴a=60,当x=-4时,y=-2×(-4)+60=68.
6、解析:选B 由题意知,==10,
==8,
∴=8-0.76×10=0.4,
∴当x=15时,=0.76×15+0.4=11.8(万元).
7、解析:选B 线性回归分析中,相关系数为r,|r|越接近于1, 相关程度越大; |r|越小, 相关程度越小,故其拟合效果最好. 故选B.
8、解析:选C ∵x=10时,y=0.8×10+2+e=10+e,又∵|e|≤0.5,∴y≤10.5.
9、解析:选C 法一:由线性回归直线方程过样本中心(176,176),排除A,B答案,结合选项可得C法二:将表中的五组数值分别代入选项验证,可知y=88+x最适合.
10、解析:选D 根据线性相关的知识,散点图中各样本点条状分布越均匀,同时保持残差平方和越小(对于已经获取的样本数据,R2的表达式中(yi-)2为确定的数,则残差平方和越小,R2越大),由回归分析建立的线性回归模型的拟合效果越好,由试验结果知丁要好些.故选D.
11.【答案】A
【解析】由给出的四组数据的散点图可以看出,
图1和图3是正相关,相关系数大于0,
图2和图4是负相关,相关系数小于0,
图1和图2的点相对更加集中,所以相关性要强,所以r1接近于1,r2接近于-1,
由此可得r2<r4<0<r3<r1.
12、解析:根据样本相关系数的定义可知, 当所有样本点都在直线上时, 相关系数为1.
答案:1
13、解析:由回归分析的概念知①④正确,②③错误.
答案:①④
14、解析:以x+1代x,得=0.254(x+1)+0.321,与=0.254x+0.321相减可得,年饮食支出平均增加0.254万元.
答案:0.254
15、解:(1)=(8+8.2+8.4+8.6+8.8+9)=8.5,
=(90+84+83+80+75+68)=80,
从而=+20=80+20×8.5=250, 故=-20x+250.
(2)由题意知, 工厂获得利润
z=(x-4)y=-20x2+330x-1 000=-202+361.25,所以当x==8.25时,
zmax=361.25(元).
即当该产品的单价定为8.25元时,工厂获得最大利润.
16、解:(1)依题意设y与x的线性回归方程为=6.5x+.
==5,==50,
∵=6.5x+经过(,),∴50=6.5×5+,∴=17.5,
∴y与x的线性回归方程为=6.5x+17.5.
(2)由(1)的线性模型得yi-i与yi-的关系如下表:
yi-i -0.5 -3.5 10 -6.5 0.5
yi- -20 -10 10 0 20
所以(yi-i)2=(-0.5)2+(-3.5)2+102+(-6.5)2+0.52=155.
(yi-)2=(-20)2+(-10)2+102+02+202=1 000.
所以R=1-=1-=0.845.
由于R=0.845,R2=0.82知R>R2,所以(1)的线性模型拟合效果比较好.
回归分析的基本思想及其初步应用
编号:111
一、选择题:
1.在对两个变量x,y进行线性回归分析时,有下列步骤:
①对所求出的回归直线方程作出解释;②收集数据(xi,yi),i=1,2,…,n;
③求线性回归方程; ④求相关系数; ⑤根据所搜集的数据绘制散点图.
如果根据可行性要求能够作出变量x,y具有线性相关的结论,
则在下列操作顺序中正确的是( )
A.①②⑤③④ B.③②④⑤①
C.②④③①⑤ D.②⑤④③①
2.有下列说法:
①在残差图中,残差点比较均匀地落在水平的带状区域内,说明选用的模型比较合适;
②R2来刻画回归的效果,R2值越大,说明模型的拟合效果越好;
③比较两个模型的拟合效果, 可以比较残差平方和的大小,残差平方和越小的模型,
拟合效果越好.
其中正确命题的个数是( )
A.0 B.1 C.2 D.3
3.下图是根据变量x,y的观测数据(xi,yi)(i=1,2,…,10)得到的散点图,由这些散点图可以判断变量x,y具有相关关系的图是( )
A.①② B.①④ C.②③ D.③④
4.已知变量x与y正相关,且由观测数据算得样本平均数=3,=3.5,则由该观测数据算得的线性回归方程可能为( )
A.=0.4x+2.3 B.=2x-2.4
C.=-2x+9.5 D.=-0.3x+4.4
5.某咖啡厅为了了解热饮的销售量y(个)与气温x(℃)之间的关系,随机统计了某4天的销售量与气温,并制作了对照表:
气温(℃) 18 13 10 -1
销售量(个) 24 34 38 64
由表中数据,得线性回归方程=-2x+a.当气温为-4 ℃时,预测销售量约为( )
A.68 B.66 C.72 D.70
6.为了解某社区居民的家庭年收入与年支出的关系,随机调查了该社区5户家庭,得到如下统计数据表:
收入x(万元) 8.2 8.6 10.0 11.3 11.9
支出y(万元) 6.2 7.5 8.0 8.5 9.8
根据上表可得回归直线方程=x+,其中=0.76,=-.据此估计,该社区一户年收入为15万元家庭的年支出为( )
A.11.4万元 B.11.8万元 C.12.0万元 D.12.2万元
7.在建立两个变量y与x的回归模型中,分别选择4个不同模型,求出它们相对应的R2如表,则其中拟合效果最好的模型是( )
模型 1 2 3 4
R2 0.67 0.85 0.49 0.23
A.模型1 B.模型2 C.模型3 D.模型4
8.如果某地的财政收入x与支出y满足线性回归方程y=bx+a+e(单位:亿元),其中b=0.8,
a=2,|e|≤0.5,如果今年该地区财政收入为10亿元,则年支出预计不会超过( )
A.10亿 B.9亿 C.10.5亿 D.9.5亿
9.为了解儿子身高与其父亲身高的关系,随机抽取5对父子的身高数据如下:
父亲身高x(cm) 174 176 176 176 178
儿子身高y(cm) 175 175 176 177 177
则y对x的线性回归方程为( ).
A.y=x-1 B.y=x+1 C.y=88+x D.y=176
10.甲、乙、丙、丁4位同学各自对A,B两变量进行回归分析,分别得到散点图与残差平方和
如下表:
甲 乙 丙 丁
散点图
残差平方和 115 106 124 103
哪位同学的试验结果体现拟合A,B两变量关系的模型拟合精度高( )
A.甲 B.乙 C.丙 D.丁
11.对四组数据进行统计,获得以下散点图,关于其相关系数的比较,正确的是( )
A.r2<r4<0<r3<r1 B.r4<r2<0<r1<r3
C.r4<r2<0<r3<r1 D.r2<r4<0<r1<r3
二、填空题:
12.在一组样本数据(x1,y1),(x2,y2),…,(xn,yn)(n≥2,x1,x2,…,xn不全相等)的散点图中,
若所有样本点(xi,yi)(i=1,2…n)都在直线y=x+1上,则这组样本数据的样本相关系数为____.
13.下列说法正确的命题是________(填序号).
①回归直线过样本点的中心(,);
②线性回归方程对应的直线=x+至少经过其样本数据点(x1,y1),(x2,y2),…,(xn,yn)中的一个点;
③在残差图中,残差点分布的带状区域的宽度越宽,其模型拟合的精度越高;
④在回归分析中,R2为0.98的模型比R2为0.80的模型拟合的效果好.
14.某地若干户家庭的年收入x(单位:万元)和年饮食支出y(单位:万元),调查显示年收入x与年饮食支出y具有线性相关关系,并由调查数据得到y对x的回归直线方程:=0.254x+0.321.由回归直线方程可知,家庭年收入每增加1万元,年饮食支出平均增加________万元.
三、解答题:
15.某工厂为了对新研发的一种产品进行合理定价,将该产品按事先拟定的价格进行试销,
得到如下数据:
单价x(元) 8 8.2 8.4 8.6 8.8 9
销量y(件) 90 84 83 80 75 68
(1)求回归直线方程=x+,其中=-20,=-;
(2)预计在今后的销售中,销量与单价仍然服从(1)中的关系,且该产品的成本是4元/件,
为使工厂获得最大利润,该产品的单价应定为多少元?(利润=销售收入-成本)
16.关于x与y有以下数据:
x 2 4 5 6 8
y 30 40 60 50 70
已知x与y线性相关,由最小二乘法得=6.5,
(1)求y与x的线性回归方程;
(2)现有第二个线性模型:=7x+17,且R2=0.82.
若与(1)的线性模型比较,哪一个线性模型拟合效果比较好,请说明理由.
1、解析:选D 对两个变量进行回归分析时,首先收集数据(xi,yi),i=1,2,…,n;根据所搜集的数据绘制散点图.观察散点图的形状,判断线性相关关系的强弱,求相关系数,写出线性回归方程,最后依据所求出的回归直线方程作出解释;故正确顺序是②⑤④③①, 故选D.
2、解析:选D ①选用的模型是否合适与残差点的分布有关; 对于②③, R2的值越大, 说明残差平方和越小, 随机误差越小,则模型的拟合效果越好.
3、解析:选D 根据散点图中点的分布情况,可判断③④中的变量x,y具有相关的关系.
4、解析:选A 依题意知,相应的回归直线的斜率应为正,排除C,D.且直线必过点(3,3.5)代入A,B得A正确.
5、解析:选A ∵=(18+13+10-1)=10,=(24+34+38+64)=40,
∴40=-2×10+a,∴a=60,当x=-4时,y=-2×(-4)+60=68.
6、解析:选B 由题意知,==10,
==8,
∴=8-0.76×10=0.4,
∴当x=15时,=0.76×15+0.4=11.8(万元).
7、解析:选B 线性回归分析中,相关系数为r,|r|越接近于1, 相关程度越大; |r|越小, 相关程度越小,故其拟合效果最好. 故选B.
8、解析:选C ∵x=10时,y=0.8×10+2+e=10+e,又∵|e|≤0.5,∴y≤10.5.
9、解析:选C 法一:由线性回归直线方程过样本中心(176,176),排除A,B答案,结合选项可得C法二:将表中的五组数值分别代入选项验证,可知y=88+x最适合.
10、解析:选D 根据线性相关的知识,散点图中各样本点条状分布越均匀,同时保持残差平方和越小(对于已经获取的样本数据,R2的表达式中(yi-)2为确定的数,则残差平方和越小,R2越大),由回归分析建立的线性回归模型的拟合效果越好,由试验结果知丁要好些.故选D.
11.【答案】A
【解析】由给出的四组数据的散点图可以看出,
图1和图3是正相关,相关系数大于0,
图2和图4是负相关,相关系数小于0,
图1和图2的点相对更加集中,所以相关性要强,所以r1接近于1,r2接近于-1,
由此可得r2<r4<0<r3<r1.
12、解析:根据样本相关系数的定义可知, 当所有样本点都在直线上时, 相关系数为1.
答案:1
13、解析:由回归分析的概念知①④正确,②③错误.
答案:①④
14、解析:以x+1代x,得=0.254(x+1)+0.321,与=0.254x+0.321相减可得,年饮食支出平均增加0.254万元.
答案:0.254
15、解:(1)=(8+8.2+8.4+8.6+8.8+9)=8.5,
=(90+84+83+80+75+68)=80,
从而=+20=80+20×8.5=250, 故=-20x+250.
(2)由题意知, 工厂获得利润
z=(x-4)y=-20x2+330x-1 000=-202+361.25,所以当x==8.25时,
zmax=361.25(元).
即当该产品的单价定为8.25元时,工厂获得最大利润.
16、解:(1)依题意设y与x的线性回归方程为=6.5x+.
==5,==50,
∵=6.5x+经过(,),∴50=6.5×5+,∴=17.5,
∴y与x的线性回归方程为=6.5x+17.5.
(2)由(1)的线性模型得yi-i与yi-的关系如下表:
yi-i -0.5 -3.5 10 -6.5 0.5
yi- -20 -10 10 0 20
所以(yi-i)2=(-0.5)2+(-3.5)2+102+(-6.5)2+0.52=155.
(yi-)2=(-20)2+(-10)2+102+02+202=1 000.
所以R=1-=1-=0.845.
由于R=0.845,R2=0.82知R>R2,所以(1)的线性模型拟合效果比较好.
