5.3.1 函数的单调性-【新教材】2020-2021学年人教A版(2019)高中数学选择性必修二练习(Word含解析)
文档属性
| 名称 | 5.3.1 函数的单调性-【新教材】2020-2021学年人教A版(2019)高中数学选择性必修二练习(Word含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 85.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-04-19 21:40:36 | ||
图片预览




文档简介
函数的单调性练习
一、单选题
函数f(x)=2x?lnx的单调递减区间为(????)
A. (?∞,12) B. (12,+∞) C. (0,12) D. (0,+∞)
直线y=a与函数y=x3?3x的图象有三个相异的交点,则实数a的取值范围为(????)
A. (?2,2) B. [?2,2] C. [2,+∞) D. (?∞,?2]
函数f?(x)=ex?ex,x∈R的单调递增区间是(? )
A. (0,+∞) B. (?∞,0) C. (?∞,1) D. (1,+∞)
已知a=1e,b=ln33,c=ln44,则a,b,c的大小关系为(? )
A. b已知函数f(x)=lnx+ax,则“a<0”是“函数f(x)在定义域内为增函数”的(????)
A. 充分不必要条件 B. 必要不充分条件
C. 充要条件 D. 既不充分也不必要条件
在R上可导的函数f?(x)的图象如图所示,则关于x的不等式xf′(x)<0的解集为(????)
A. (?∞,?1)∪(0,1) B. (?1,0)∪(1,+∞)
C. (?2,?1)∪(1,2) D. (?∞,?2)∪(2,+∞)
f(x)是定义在(0,+∞)上的非负可导函数,且满足xf′(x)+f(x)<0,对任意正数a,b,若a A. af(b)已知y=fx为R上的可导函数,当x≠0时,f′(x)+fxx>0,则关于x的函数g(x)=f(x)+1x的零点个数为
A. 1 B. 2 C. 0 D. 0或2
已知定义在R上的可导函数f(x)的导函数为f′(x),满足f′(x) A. (?2,+∞) B. (0,+∞) C. (1,+∞) D. (2,+∞)
若函数在区间(12,2)内存在单调递增区间,则实数a的取值范围是(? ??)
A. B. C. (?2,?18) D.
设f(x)是定义在R上的奇函数,f(2)=0,当x>0时,有xf′(x)?f(x)x2?<0恒成立,则f(x)x>0的解集为(? ? ? ? ? )
A. (?2,0)∪(2,+∞) B. (?2,0)∪(0,2)
C. (?∞,?2)∪(2,+∞) D. (?∞,?2)∪(0,2)
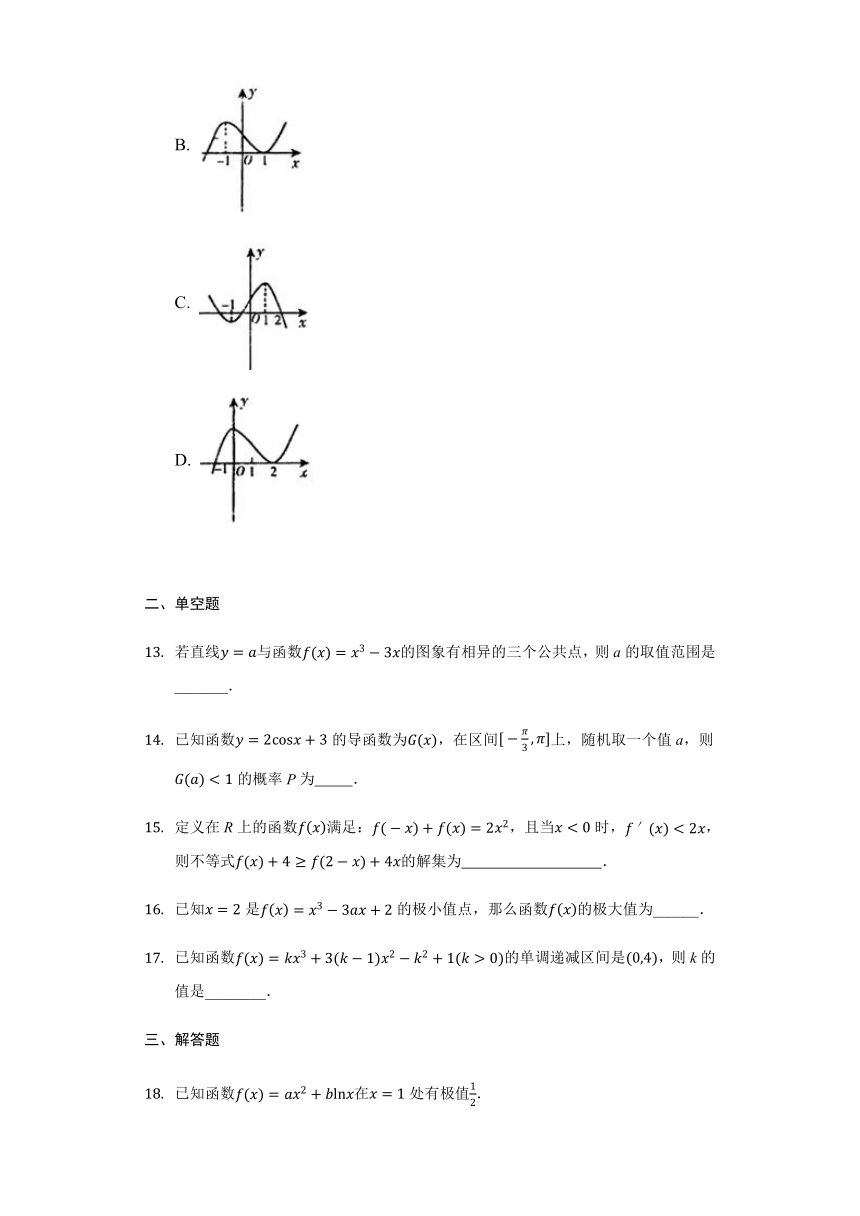
已知函数y=?xf′x的图象如图(其中f′x是函数fx的导函数),下面四个图象中,y=fx的图象可能是(? ? )
A.
B.
C.
D.
二、单空题
若直线y=a与函数f(x)=x3?3x的图象有相异的三个公共点,则a的取值范围是_______.
已知函数y=2cosx+3的导函数为G(x),在区间[?π3,π]上,随机取一个值a,则G(a)<1的概率P为??????????.
定义在R上的函数fx满足:f(?x)+f(x)=2x2,且当x<0时,f′(x)<2x,则不等式f(x)+4≥f(2?x)+4x的解集为? ? ? ? ? ? ? ? ? ? ? ? ?.
已知x=2是fx=x3?3ax+2的极小值点,那么函数fx的极大值为______.
已知函数f(x)=kx3+3(k?1)x2?k2+1(k>0)的单调递减区间是(0,4),则k的值是________.
三、解答题
已知函数f(x)=ax2+blnx在x=1处有极值12.
(1)求实数a、b的值;
(2)判断函数f(x)的单调区间,并求极值.
已知函数f(x)=ax+lnx,g(x)=12bx2?2x+2,a,b∈R.
(1)求函数f(x)的单调区间;
(2)记函数?(x)=f(x)+g(x),当a=0时,?(x)在(0,1)上有且只有一个极值点,求实数b的取值范围.
已知函数f(x)=ex(x2+ax+1).
(Ⅰ)当a∈R时,讨论f?(x)的单调性;
(Ⅱ)若实数a满足a≤?1,且函数g(x)=4x3+3(b+4)x2+6(b+2)x(b∈R)的极小值点与f?(x)的极小值点相同,求证:g(x)的极小值小于等于0.
答案和解析
1.【答案】C
【解答】
解:f(x))=2x?lnx的定义域为(0,+∞).
f′(x)=2?1x=2x?1x,
令f′(x)<0,解得0所以函数f(x)=2x?lnx的单调减区间是(0,12).
2.【答案】A
【解答】
解:y=x3?3x的导数y′=3x2?3=3(x?1)·(x+1),
令y′>0可解得x1,
故y=x3?3x在(?∞,?1),(1,+∞)上单调递增,在(?1,1)上单调递减,
函数的极大值为f?(?1)=2,极小值为f?(1)=?2,
大致图象如图所示,而y=a为一条水平直线,
通过图象可得,y=a介于极大值与极小值之间,则有三个相异交点,可得a∈(?2,2).
故选:A.
3.【答案】D
【解答】
解:f′(x)=ex?e,
令f′(x)>0得x>1,
∴函数f(x)的单调递增区间为(1,+∞).
4.【答案】B
【解答】
解:设f(x)=lnxx,x?e,则f′(x)=1?lnxx2?0恒成立,
∴函数f(x)在[e,+∞)上单调递减,∴fe>f3>f4,即lnee=1e>ln33>ln44,
∴a>b>c,故选B.
5.【答案】A
【解答】
解:f′(x)=1x?ax2=x?ax2,x>0,
当a<0时,f′(x)>0,f(x)在(0,+∞)上单调递增,
当函数f(x)在定义域内为增函数时,可得f′(x)≥0在(0,+∞)上恒成立,即a≤0,
故函数f(x)=lnx+ax,则“a<0”是“函数f(x)在定义域内为增函数”的充分不必要条件.
6.【答案】A
【解答】
解:在(?∞,?1)和(1,+∞)上,f?(x)单调递增,
所以f′(x)>0,使xf′(x)<0的x的范围为(?∞,?1);
在(?1,1)上,f?(x)单调递减,
所以f′(x)<0,使xf′(x)<0的范围为(0,1).
综上,关于x的不等式xf′(x)<0的解集为(?∞,?1)∪(0,1).
7.【答案】C
【解答】
解:设g(x)=xf(x),x>0,
则g′(x)=[xf(x)]′=xf′(x)+f(x)<0,
∴函数g(x)在(0,+∞)上是减函数,
∵ag(b)
即bf?(b)8.【答案】C
【解答】
解:由于函数g(x)=f(x)+1x,可得x≠0,因而g(x)的零点跟xg(x)的非零零点是完全一样的,
故我们考虑xg(x)=xf(x)+1的零点.
由于当x≠0时,f′(x)+f(x)x>0,
①当x>0时,(x?g(x))′=(xf(x))′=xf′(x)+f(x)=x(f′(x)+f(x)x)>0,
?所以,在(0,+∞)上,函数x?g(x)单调递增函数.
又∵x→0lim[xf(x)+1]=1,∴在(0,+∞)上,函数x?g(x)=xf(x)+1>1恒成立,
因此,在(0,+∞)上,函数x?g(x)=xf(x)+1没有零点.
②当x<0时,由于(x?g(x))′=(xf(x))′=xf′(x)+f(x)=x(f′(x)+f(x)x)<0,
故函数x?g(x)在(?∞,0)上是递减函数,函数x?g(x)=xf(x)+1>1恒成立,
故函数x?g(x)在(?∞,0)上无零点.
综上可得,函g(x)=f(x)+1x在R上的零点个数为0,
9.【答案】D
【解答】
解:构造g(x)=f(x)???12x2+1,
则g′(x)=f′(x)???x<0,
所以g(x)是R上的单调减函数,
又因为,f(2)=1,g(2)=0,
所以不等式f(x)<12x2?1可化为g(x)由函数单调递减可得x>2,
故不等式的解集为(2,+∞).
10.【答案】D
【解答】
解:根据题意得,f′x=1x+2ax,
∵f(x)在区间(12,2)内存在单调递增区间,
∴f′x>0在(12,2)内有解,
即1x+2ax>0?a>?12x2在(12,2)内有解
故存在x∈(12,2),使得a>?12x2,
令g(x)=?12x2,则g(x)在(12,2)单调递增,
所以g(x)∈(?2,?18),
故a>?2.
11.【答案】B
【解答】
解:设函数g(x)=f(x)x,?则g′(x)=xf′(x)?f(x)x2,
?∵当x>0时,有xf′(x)?f(x)x2<0成立,?
∴当x>0时,g′(x)<0,?
∴g(x)=f(x)x在(0,+∞)上单调递减,?
∵函数f(x)是定义在R上的奇函数,f(2)=0,?
∴g(?x)=f(?x)?x=?f(x)?x=g(x),
?∴g(x)为偶函数,且g(2)=0,??
∴g(x)的单调递增区间为(?∞,0),
∵f(2)=0,
∴g(?2)=0,g(2)=0,
∴当x0,当00,当x>2时,g(x)<0.
∴解集为(?2,0)∪(0,2).
故选B.
12.【答案】B
【解答】
解:由已知图象可得,
当x0,y>0所以f′(x)>0,即函数f(x)单增,
当?10,y<0所以f′(x)<0,即函数f(x)单减,
当00所以f′(x)<0,即函数f(x)单减,
当x>1时,?x<0,y<0所以f′(x)>0,即函数f(x)单增,
所以f(x)单增区间为?∞,?1,1,+∞,单减区间为(?1,1).
13.【答案】(?2,2)
【解析】
解:∵函数f(x)=x3?3x,
∴f′(x)=3x2?3=3(x+1)(x?1).
∴当x∈(?∞,?1)∪(1,+∞)时,f′(x)>0,
∴函数f(x)在区间(?∞,?1),(1,+∞)上单调递增;
当x∈(?1,1)时,f′(x)<0,
∴函数f(x)在区间(?1,1)上单调递减.
故当x=?1时,f(x)取极大值f(?1)=?1+3=2,
当x=1时,f(x)取极小值f(1)=1?3=?2,
又f(x)=0,解得x=0,±3.
当x→+∞,f(x)→+∞,
当x→?∞,f(x)→?∞,
根据以上画出图象:
若函数f(x)=x3?3x的图象与直线y=a有相异三个公共点,
则?2故答案为(?2,2).
14.【答案】78
【解答】解:由题意,知G(x)=y′=?2sinx,
在区间[?π3,π]上,由G(a)=?2sina<1,得a∈(?π6,π],
故概率P=π?(?π6)π?(?π3)=78.
故答案为78.
15.【答案】?
?【解答】
解:根据题意,令g(x)=f(x)?x2,
若f(x)+f(?x)=2x2,变形有f(x)?x2+f(?x)?(?x)2=0,
即g(x)+g(?x)=0,
故g(x)为奇函数,
由g(x)=f(x)?x2,则g′(x)=f′(x)?2x,
又当x<0时,f′(x)<2x,则x<0时,g′(x)=f′(x)?2x<0恒成立,
即g(x)在(?∞,0)上为减函数,
又由g(x)为奇函数,则g(x)在(0,+∞)上也为减函数,
因为当x=0时,f(0)=0,
则g(0)=f(0)?02=0,
综上所述g(x)为R上的减函数,
则不等式f(x)+4?f(2?x)+4x,即f(x)?x2?f(2?x)+4x?4?x2,
所以f(x)?x2?f(2?x)?2?x2,即gx≥g2?x,
则有x≤2?x,解得x≤1,
故不等式f(x)+4?f(2?x)+4x的解集为.
故答案为.
16.【答案】18
【解答】
解:f′x=3x2?3a,
因为x=2是极小值点,所以f′2=0,
即12?3a=0,得a=4,fx=x3?12x+2,
令f′x=3x2?12=0,得x=2或x=?2,
所以可得f(x)的极大值为f?2=?23?12×?2+2=18.
故答案为18.
17.【答案】13
【解答】
解:∵f(x)=kx3+3(k?1)x2?k2+1,
∴f′(x)=3kx2+6(k?1)x=3kx(x+2k?2k).
∵函数f(x)的单调递减区间是(0,4),
∴?2k?2k=4.
∴k=13.
18.【答案】解:(1)因为f(x)=ax2+blnx,所以f′(x)=2ax+bx.
又函数f(x)在x=1处有极值12,
故f′(1)=0,f(1)=12即2a+b=0a=12,
可得a=12,b=?1.
(2)由(1)可知f(x)=12x2?lnx.其定义域为(0,+∞),
且f′(x)=x?1x=(x+1)(x?1)x.令f′(x)=0,则x=?1(舍去)或x=1.
当x变化时,f′(x),f(x)的变化情况如表:
x
(0,1)
1
(1,+∞)
f′(x)
?
0
+
f(x)
↘
极小值
↗
所以函数f(x)的单调递减区间是(0,1),单调递增区间是(1,+∞),且函数f(x)在定义域上只有极小值f(1)=12,而无极大值.
19.【答案】解:的定义域是(0,+∞),
且?f′(x)=?ax2+1x=x?ax2;
①若a?0,则f′(x)>0,f(x)的单调增区间是(0,+∞),
②若a>0,令f′(x)=0,得x=a,
当0a时,f′(x)>0,
∴f(x)的单调减区间是(0,a),单调增区间是(a,+∞);
综上,当a?0时,f(x)的单调增区间是(0,+∞),无单调减区间;
当a>0时,f(x)的单调减区间是(0,a),单调增区间是(a,+∞);
(2)a=0时,,
∴?′(x)=bx?2+1x=bx2?2x+1x?,
∵?(x)在(0,1)上有且只有一个极值点,
则?′(x)=0在(0,1)上有唯一实数解,且两侧异号,
由?′(x)=0,得bx2?2x+1=0;
令p(x)=bx2?2x+1,则p(x)在(0,1)上有且只有一个零点,
易知p(0)=1>0,
①当b=0,由p(x)=0,得x=12,满足题意;
②当b>0时,由Δ=4?4b>0p1=b?1<0,解得0③当b<0时,Δ=4?4b>0p1=b?1<0,得b<1,故b<0;
综上所述,?(x)在(0,1)上有且只有一个极值点时,b<1.
故实数b的取值范围为?∞,1.
20.【答案】解:(Ⅰ)f′(x)=ex[x2+(a+2)x+a+1]
f′(x)=ex(x+1)(x+a+1)
由f′(x)=0,得x=?1,或x=?a?1
(1)当a=0时,f′(x)=ex(x+1)2≥0,f(x)在(?∞,+∞)上为增函数,
(2)当a>0时,f′(x)>0解得x∈(?∞,?a?1)或x∈(?1,+∞),f′(x)<0解得x∈(?a?1,?1),
故当a>0时f(x)在(?∞,?a?1)、(?1,+∞)上为增函数,f(x)在(?a?1,?1)上为减函数;
(3)当a<0时,f′(x)>0解得x∈(?∞,?1)或x∈(?a?1,+∞),f′(x)<0解得x∈(?1,?a?1),
故当a<0时f(x)在(?∞,?1)、(?a?1,+∞)上为增函数,f(x)在(?1,?a?1)上为减函数;
(Ⅱ)∵a≤?1,∴?a?1>?1,
又f′(x)=ex[x2+(a+2)x+a+1]=ex(x+a+1)(x+1),
∴f(x)的极小值是x=?a?1,从而g(x)的极小值点也是x=?a?1
又g′(x)=12(x+1)(x+b+22)
∴?b+22=?a?1,即b=2a,
因为a≤?1,
故g(x)的极小值g(?a?1)=?(1+a)2(4?2a)≤0,
即g(x)的极小值小于等于0.
一、单选题
函数f(x)=2x?lnx的单调递减区间为(????)
A. (?∞,12) B. (12,+∞) C. (0,12) D. (0,+∞)
直线y=a与函数y=x3?3x的图象有三个相异的交点,则实数a的取值范围为(????)
A. (?2,2) B. [?2,2] C. [2,+∞) D. (?∞,?2]
函数f?(x)=ex?ex,x∈R的单调递增区间是(? )
A. (0,+∞) B. (?∞,0) C. (?∞,1) D. (1,+∞)
已知a=1e,b=ln33,c=ln44,则a,b,c的大小关系为(? )
A. b
A. 充分不必要条件 B. 必要不充分条件
C. 充要条件 D. 既不充分也不必要条件
在R上可导的函数f?(x)的图象如图所示,则关于x的不等式xf′(x)<0的解集为(????)
A. (?∞,?1)∪(0,1) B. (?1,0)∪(1,+∞)
C. (?2,?1)∪(1,2) D. (?∞,?2)∪(2,+∞)
f(x)是定义在(0,+∞)上的非负可导函数,且满足xf′(x)+f(x)<0,对任意正数a,b,若a
A. 1 B. 2 C. 0 D. 0或2
已知定义在R上的可导函数f(x)的导函数为f′(x),满足f′(x)
若函数在区间(12,2)内存在单调递增区间,则实数a的取值范围是(? ??)
A. B. C. (?2,?18) D.
设f(x)是定义在R上的奇函数,f(2)=0,当x>0时,有xf′(x)?f(x)x2?<0恒成立,则f(x)x>0的解集为(? ? ? ? ? )
A. (?2,0)∪(2,+∞) B. (?2,0)∪(0,2)
C. (?∞,?2)∪(2,+∞) D. (?∞,?2)∪(0,2)
已知函数y=?xf′x的图象如图(其中f′x是函数fx的导函数),下面四个图象中,y=fx的图象可能是(? ? )
A.
B.
C.
D.
二、单空题
若直线y=a与函数f(x)=x3?3x的图象有相异的三个公共点,则a的取值范围是_______.
已知函数y=2cosx+3的导函数为G(x),在区间[?π3,π]上,随机取一个值a,则G(a)<1的概率P为??????????.
定义在R上的函数fx满足:f(?x)+f(x)=2x2,且当x<0时,f′(x)<2x,则不等式f(x)+4≥f(2?x)+4x的解集为? ? ? ? ? ? ? ? ? ? ? ? ?.
已知x=2是fx=x3?3ax+2的极小值点,那么函数fx的极大值为______.
已知函数f(x)=kx3+3(k?1)x2?k2+1(k>0)的单调递减区间是(0,4),则k的值是________.
三、解答题
已知函数f(x)=ax2+blnx在x=1处有极值12.
(1)求实数a、b的值;
(2)判断函数f(x)的单调区间,并求极值.
已知函数f(x)=ax+lnx,g(x)=12bx2?2x+2,a,b∈R.
(1)求函数f(x)的单调区间;
(2)记函数?(x)=f(x)+g(x),当a=0时,?(x)在(0,1)上有且只有一个极值点,求实数b的取值范围.
已知函数f(x)=ex(x2+ax+1).
(Ⅰ)当a∈R时,讨论f?(x)的单调性;
(Ⅱ)若实数a满足a≤?1,且函数g(x)=4x3+3(b+4)x2+6(b+2)x(b∈R)的极小值点与f?(x)的极小值点相同,求证:g(x)的极小值小于等于0.
答案和解析
1.【答案】C
【解答】
解:f(x))=2x?lnx的定义域为(0,+∞).
f′(x)=2?1x=2x?1x,
令f′(x)<0,解得0
2.【答案】A
【解答】
解:y=x3?3x的导数y′=3x2?3=3(x?1)·(x+1),
令y′>0可解得x1,
故y=x3?3x在(?∞,?1),(1,+∞)上单调递增,在(?1,1)上单调递减,
函数的极大值为f?(?1)=2,极小值为f?(1)=?2,
大致图象如图所示,而y=a为一条水平直线,
通过图象可得,y=a介于极大值与极小值之间,则有三个相异交点,可得a∈(?2,2).
故选:A.
3.【答案】D
【解答】
解:f′(x)=ex?e,
令f′(x)>0得x>1,
∴函数f(x)的单调递增区间为(1,+∞).
4.【答案】B
【解答】
解:设f(x)=lnxx,x?e,则f′(x)=1?lnxx2?0恒成立,
∴函数f(x)在[e,+∞)上单调递减,∴fe>f3>f4,即lnee=1e>ln33>ln44,
∴a>b>c,故选B.
5.【答案】A
【解答】
解:f′(x)=1x?ax2=x?ax2,x>0,
当a<0时,f′(x)>0,f(x)在(0,+∞)上单调递增,
当函数f(x)在定义域内为增函数时,可得f′(x)≥0在(0,+∞)上恒成立,即a≤0,
故函数f(x)=lnx+ax,则“a<0”是“函数f(x)在定义域内为增函数”的充分不必要条件.
6.【答案】A
【解答】
解:在(?∞,?1)和(1,+∞)上,f?(x)单调递增,
所以f′(x)>0,使xf′(x)<0的x的范围为(?∞,?1);
在(?1,1)上,f?(x)单调递减,
所以f′(x)<0,使xf′(x)<0的范围为(0,1).
综上,关于x的不等式xf′(x)<0的解集为(?∞,?1)∪(0,1).
7.【答案】C
【解答】
解:设g(x)=xf(x),x>0,
则g′(x)=[xf(x)]′=xf′(x)+f(x)<0,
∴函数g(x)在(0,+∞)上是减函数,
∵a
即bf?(b)
【解答】
解:由于函数g(x)=f(x)+1x,可得x≠0,因而g(x)的零点跟xg(x)的非零零点是完全一样的,
故我们考虑xg(x)=xf(x)+1的零点.
由于当x≠0时,f′(x)+f(x)x>0,
①当x>0时,(x?g(x))′=(xf(x))′=xf′(x)+f(x)=x(f′(x)+f(x)x)>0,
?所以,在(0,+∞)上,函数x?g(x)单调递增函数.
又∵x→0lim[xf(x)+1]=1,∴在(0,+∞)上,函数x?g(x)=xf(x)+1>1恒成立,
因此,在(0,+∞)上,函数x?g(x)=xf(x)+1没有零点.
②当x<0时,由于(x?g(x))′=(xf(x))′=xf′(x)+f(x)=x(f′(x)+f(x)x)<0,
故函数x?g(x)在(?∞,0)上是递减函数,函数x?g(x)=xf(x)+1>1恒成立,
故函数x?g(x)在(?∞,0)上无零点.
综上可得,函g(x)=f(x)+1x在R上的零点个数为0,
9.【答案】D
【解答】
解:构造g(x)=f(x)???12x2+1,
则g′(x)=f′(x)???x<0,
所以g(x)是R上的单调减函数,
又因为,f(2)=1,g(2)=0,
所以不等式f(x)<12x2?1可化为g(x)
故不等式的解集为(2,+∞).
10.【答案】D
【解答】
解:根据题意得,f′x=1x+2ax,
∵f(x)在区间(12,2)内存在单调递增区间,
∴f′x>0在(12,2)内有解,
即1x+2ax>0?a>?12x2在(12,2)内有解
故存在x∈(12,2),使得a>?12x2,
令g(x)=?12x2,则g(x)在(12,2)单调递增,
所以g(x)∈(?2,?18),
故a>?2.
11.【答案】B
【解答】
解:设函数g(x)=f(x)x,?则g′(x)=xf′(x)?f(x)x2,
?∵当x>0时,有xf′(x)?f(x)x2<0成立,?
∴当x>0时,g′(x)<0,?
∴g(x)=f(x)x在(0,+∞)上单调递减,?
∵函数f(x)是定义在R上的奇函数,f(2)=0,?
∴g(?x)=f(?x)?x=?f(x)?x=g(x),
?∴g(x)为偶函数,且g(2)=0,??
∴g(x)的单调递增区间为(?∞,0),
∵f(2)=0,
∴g(?2)=0,g(2)=0,
∴当x0,当0
∴解集为(?2,0)∪(0,2).
故选B.
12.【答案】B
【解答】
解:由已知图象可得,
当x0,y>0所以f′(x)>0,即函数f(x)单增,
当?1
当0
当x>1时,?x<0,y<0所以f′(x)>0,即函数f(x)单增,
所以f(x)单增区间为?∞,?1,1,+∞,单减区间为(?1,1).
13.【答案】(?2,2)
【解析】
解:∵函数f(x)=x3?3x,
∴f′(x)=3x2?3=3(x+1)(x?1).
∴当x∈(?∞,?1)∪(1,+∞)时,f′(x)>0,
∴函数f(x)在区间(?∞,?1),(1,+∞)上单调递增;
当x∈(?1,1)时,f′(x)<0,
∴函数f(x)在区间(?1,1)上单调递减.
故当x=?1时,f(x)取极大值f(?1)=?1+3=2,
当x=1时,f(x)取极小值f(1)=1?3=?2,
又f(x)=0,解得x=0,±3.
当x→+∞,f(x)→+∞,
当x→?∞,f(x)→?∞,
根据以上画出图象:
若函数f(x)=x3?3x的图象与直线y=a有相异三个公共点,
则?2
14.【答案】78
【解答】解:由题意,知G(x)=y′=?2sinx,
在区间[?π3,π]上,由G(a)=?2sina<1,得a∈(?π6,π],
故概率P=π?(?π6)π?(?π3)=78.
故答案为78.
15.【答案】?
?【解答】
解:根据题意,令g(x)=f(x)?x2,
若f(x)+f(?x)=2x2,变形有f(x)?x2+f(?x)?(?x)2=0,
即g(x)+g(?x)=0,
故g(x)为奇函数,
由g(x)=f(x)?x2,则g′(x)=f′(x)?2x,
又当x<0时,f′(x)<2x,则x<0时,g′(x)=f′(x)?2x<0恒成立,
即g(x)在(?∞,0)上为减函数,
又由g(x)为奇函数,则g(x)在(0,+∞)上也为减函数,
因为当x=0时,f(0)=0,
则g(0)=f(0)?02=0,
综上所述g(x)为R上的减函数,
则不等式f(x)+4?f(2?x)+4x,即f(x)?x2?f(2?x)+4x?4?x2,
所以f(x)?x2?f(2?x)?2?x2,即gx≥g2?x,
则有x≤2?x,解得x≤1,
故不等式f(x)+4?f(2?x)+4x的解集为.
故答案为.
16.【答案】18
【解答】
解:f′x=3x2?3a,
因为x=2是极小值点,所以f′2=0,
即12?3a=0,得a=4,fx=x3?12x+2,
令f′x=3x2?12=0,得x=2或x=?2,
所以可得f(x)的极大值为f?2=?23?12×?2+2=18.
故答案为18.
17.【答案】13
【解答】
解:∵f(x)=kx3+3(k?1)x2?k2+1,
∴f′(x)=3kx2+6(k?1)x=3kx(x+2k?2k).
∵函数f(x)的单调递减区间是(0,4),
∴?2k?2k=4.
∴k=13.
18.【答案】解:(1)因为f(x)=ax2+blnx,所以f′(x)=2ax+bx.
又函数f(x)在x=1处有极值12,
故f′(1)=0,f(1)=12即2a+b=0a=12,
可得a=12,b=?1.
(2)由(1)可知f(x)=12x2?lnx.其定义域为(0,+∞),
且f′(x)=x?1x=(x+1)(x?1)x.令f′(x)=0,则x=?1(舍去)或x=1.
当x变化时,f′(x),f(x)的变化情况如表:
x
(0,1)
1
(1,+∞)
f′(x)
?
0
+
f(x)
↘
极小值
↗
所以函数f(x)的单调递减区间是(0,1),单调递增区间是(1,+∞),且函数f(x)在定义域上只有极小值f(1)=12,而无极大值.
19.【答案】解:的定义域是(0,+∞),
且?f′(x)=?ax2+1x=x?ax2;
①若a?0,则f′(x)>0,f(x)的单调增区间是(0,+∞),
②若a>0,令f′(x)=0,得x=a,
当0
∴f(x)的单调减区间是(0,a),单调增区间是(a,+∞);
综上,当a?0时,f(x)的单调增区间是(0,+∞),无单调减区间;
当a>0时,f(x)的单调减区间是(0,a),单调增区间是(a,+∞);
(2)a=0时,,
∴?′(x)=bx?2+1x=bx2?2x+1x?,
∵?(x)在(0,1)上有且只有一个极值点,
则?′(x)=0在(0,1)上有唯一实数解,且两侧异号,
由?′(x)=0,得bx2?2x+1=0;
令p(x)=bx2?2x+1,则p(x)在(0,1)上有且只有一个零点,
易知p(0)=1>0,
①当b=0,由p(x)=0,得x=12,满足题意;
②当b>0时,由Δ=4?4b>0p1=b?1<0,解得0
综上所述,?(x)在(0,1)上有且只有一个极值点时,b<1.
故实数b的取值范围为?∞,1.
20.【答案】解:(Ⅰ)f′(x)=ex[x2+(a+2)x+a+1]
f′(x)=ex(x+1)(x+a+1)
由f′(x)=0,得x=?1,或x=?a?1
(1)当a=0时,f′(x)=ex(x+1)2≥0,f(x)在(?∞,+∞)上为增函数,
(2)当a>0时,f′(x)>0解得x∈(?∞,?a?1)或x∈(?1,+∞),f′(x)<0解得x∈(?a?1,?1),
故当a>0时f(x)在(?∞,?a?1)、(?1,+∞)上为增函数,f(x)在(?a?1,?1)上为减函数;
(3)当a<0时,f′(x)>0解得x∈(?∞,?1)或x∈(?a?1,+∞),f′(x)<0解得x∈(?1,?a?1),
故当a<0时f(x)在(?∞,?1)、(?a?1,+∞)上为增函数,f(x)在(?1,?a?1)上为减函数;
(Ⅱ)∵a≤?1,∴?a?1>?1,
又f′(x)=ex[x2+(a+2)x+a+1]=ex(x+a+1)(x+1),
∴f(x)的极小值是x=?a?1,从而g(x)的极小值点也是x=?a?1
又g′(x)=12(x+1)(x+b+22)
∴?b+22=?a?1,即b=2a,
因为a≤?1,
故g(x)的极小值g(?a?1)=?(1+a)2(4?2a)≤0,
即g(x)的极小值小于等于0.
