5.3.2 函数的极值与最大(小)值-【新教材】2020-2021学年人教A版(2019)高中数学选择性必修二练习(Word含解析)
文档属性
| 名称 | 5.3.2 函数的极值与最大(小)值-【新教材】2020-2021学年人教A版(2019)高中数学选择性必修二练习(Word含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 96.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-04-19 21:42:09 | ||
图片预览




文档简介
函数的极值与最大(小)值练习
一、单选题
已知函数f(x)=?x3+ax2?4在x=2处取得极值,若m∈[?1,1],则f(m)的最小值为(??? )
A. ?4 B. ?2 C. 0 D. 2
若函数fx=x3?3x在a,6?a2上有最小值,则实数a的取值范围为(??? ).
A. ?5,1 B. ?5,1 C. [?2,1) D. ?5,?2
设函数fx=x2?3ex,则(??? )
A. fx有极大值且为最大值
B. fx有极小值,但无最小值
C. 若方程fx=b恰有3个实根,则0D. 若方程fx=b恰有一个实根,则b>6e3
已知函数f(x)=13x3?4x+4在区间(2a?5,a2)上存在最大值,则实数a的取值范围是(? ?)
A. ?2,32 B. (?2,2) C. [?2,2] D. ?2,32
已知函数f(x)=aexx(a>0),下面描述正确的是
A. f(x)在R上单调递增
B. f(x)无极值点
C. 当a=2时,函数f(x)在[1,2]上有最小值e
D. 若f(x)≥1对任意x∈(0,+∞)恒成立,则a≥1e
函数f(x)=xln?x,正确的命题是(????)
A. 值域为R B. 在(1,+∞)是增函数
C. f(x)有两个不同的零点 D. 过(1,0)点的切线有两条
已知函数f(x)=12x?sinx,x∈(0,π),则f(x)的最小值为(????)
A. π6 B. π?336 C. π+336 D. 32
已知函数fx=exx+klnx?x,若x=1是函数f(x)的唯一极值点,则实数k的取值范围是(????)
A. (?∞,e] B. (?∞,e) C. (?e,+∞) D. [?e,+∞)
函数f(x)=xln?x,正确的命题是(????)
A. 值域为R B. 在(1,+∞)是增函数
C. f(x)有两个不同的零点 D. 过(1,0)点的切线有两条
已知函数fx=ax2+bx?lnx(a>0,b∈R),若对任意x>0,有fx≥f1,则(??? )
A. lna?2b C. lna=?2b D. lna≥?2b
函数f(x)=13x3+ax2?2x+1在x∈(1,2)内存在极值点,则(????)
A. ?12C. a12 D. a≤?12或a≥12
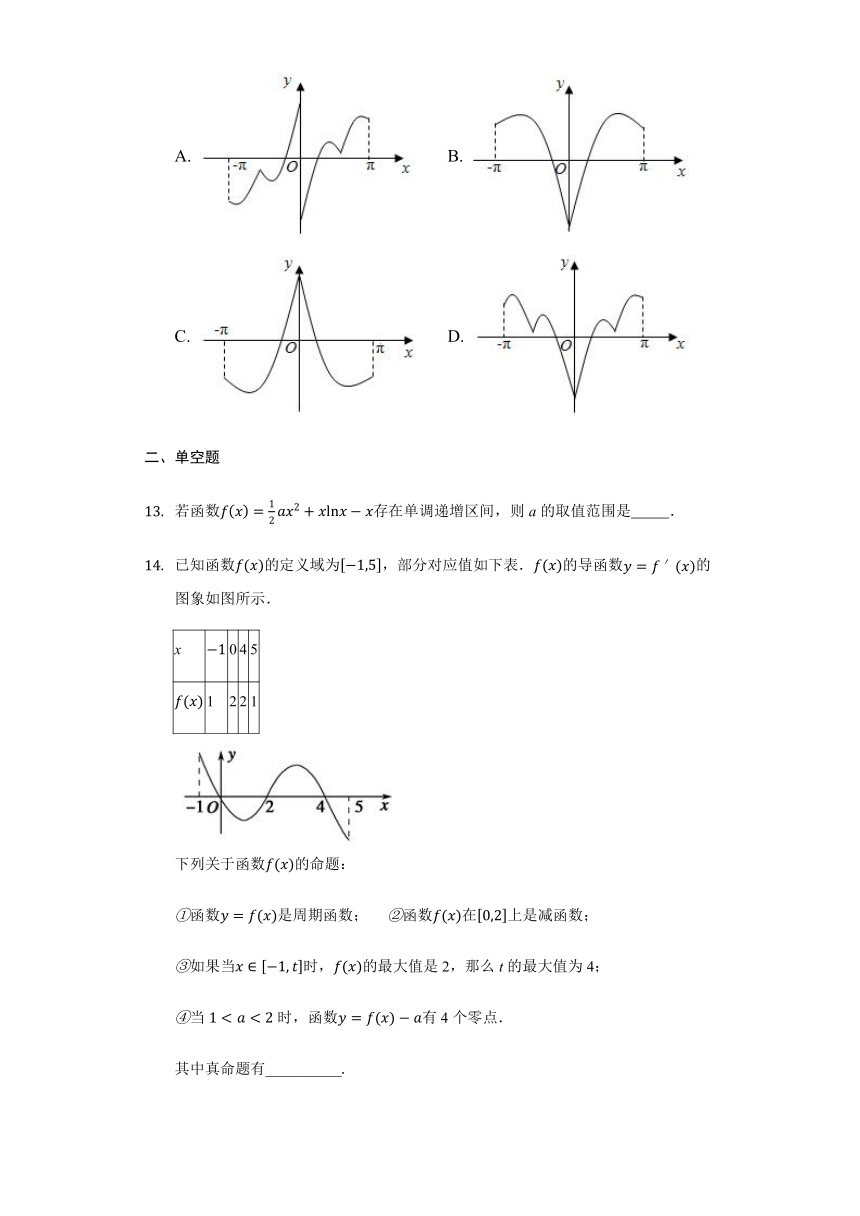
函数f(x)=ln|x|+|sinx|(?π≤x≤π且x≠0)的图象大致是(????)
A. B.
C. D.
二、单空题
若函数fx=12ax2+xlnx?x存在单调递增区间,则a的取值范围是??????????.
已知函数f(x)的定义域为?1,5,部分对应值如下表.f(x)的导函数y=f′(x)的图象如图所示.
x
?1
0
4
5
f(x)
1
2
2
1
下列关于函数f(x)的命题:
①函数y=f(x)是周期函数;??? ②函数f(x)在0,2上是减函数;
③如果当x∈?1,t时,f(x)的最大值是2,那么t的最大值为4;
④当1其中真命题有__________.?????
若对任意正实数x,y,不等式(2x?y)?(lny?lnx+1)≤xa恒成立,则实数a的取值范围a为__________
已知函数f(x)=x3+ax2+bx+c在x=?23与x=1处都取得极值,则a+b=_________.若对x∈[?1,2],不等式f(x)函数f(x)=sinx+12sin2x的最大值为________.
设函数fx=lnx+k+1,gx=ex.若fx1=gx2,且x1?x2的最小值为?1,则实数k的值是? ? ? ? ??
三、解答题
某种商品每件进价9元,售价20元,每天可卖出69件.若售价降低,销售量可以增加,且售价降低x(0≤x≤11)元时,每天多卖出的件数与x2+x成正比.已知商品售价降低3元时,一天可多卖出36件.
(1)试将该商品一天的销售利润表示成x的函数;
(2)该商品售价为多少元时一天的销售利润最大?
已知函数f(x)=x3+bx2+cx,(b,c∈R)
(1)当c=1时,讨论函数f(x)单调性;
(2)设x1,x2是函数f(x)的两个极值点,当|x1?x2|=2时,求f(1)的最小值.
答案和解析
1.【答案】A
【解答】
解:f′(x)=?3x2+2ax,因为f(x)在x=2处取得极值,所以f′(2)=0,即?12+4a=0,所以a=3,
?则f′(x)=?3x2+6x=3x(?x+2),当?10,f(x)单调递增,
所以当m∈?1,1,则fm的最小值为f(0)=?4.
2.【答案】C
【解析】解:由f(x)=x3?3x,得f′(x)=3x2?3.
令f′(x)=3x2?3=0,可得x=±1.
x∈(?∞,?1)时,f′(x)>0;x∈(?1,1)时,f′(x)<0;
x∈(1,+∞)时,f′(x)>0,
∴f(x)的增区间是(?∞,?1),(1,+∞),减区间是(?1,1),
x=1为函数的极小值点,x=?1为函数的极大值点.
∵函数?f(x)在区间(a,6?a2)上有最小值,
所以函数f(x)的极小值点必在区间(a,6?a2)内,则a<1<6?a2f(a)=a3?3a≥f(1)=?2,
解得:?2≤a<1,
∴实数a的取值范围是[?2,1),
3.【答案】C
【解答】
解:∵f(x)=(x2?3)ex,∴f′(x)=2xex+(x2?3)ex=(x+3)(x?1)ex,
∴当x∈(?∞,?3)∪(1,+∞)时,f′(x)>0,函数f(x)单调递增;
当x∈(?3,1)时,f′(x)<0,函数f(x)单调递减;
∵当x∈(?∞,?3)时,x2?3>0,ex>0,∴f(x)>0,
再由f(?3)=6e3如图,
由图象可知,f(?3)为函数的极大值但不是最大值,故A错误;
f(1)为函数的极小值,且为最小值,故B错误;
若要使f(x)=b有3个实根,
则要使函数y=b的图象与函数f(x)的图象有3个交点,
则0若要使f(x)=b恰有一个实根,
则要使函数y=b的图象与函数f(x)的图象仅有1个交点,
则b>6e3或b=?2e,故D错误.
4.【答案】D
解:f′x=x2?4,令f′x=0,则x=±2,
则当x0,函数单调递增;
当?2当x>2时,f′x>0,函数单调递增.
所以x=?2时,函数f(x)取得极大值283,
且当x=4时,f(4)=283,
要使函数f(x)=13x3?4x+4在区间(2a?5,a2)上存在最大值,
则必有:2a?55.【答案】D
【解答】
解:∵f′(x)=aex(x?1)x2,
令f′x>0得x>1,令f′x<0得x<0或0故f(x)在(?∞,0),(0,1)上单调递减,在(1,+∞)上单调递增,所以A错;
f(x)有极小值f(1)=ae,无极大值,所以B错;
当a=2时,f(x)在[1,2]上单调递增,所以f(x)min=f(1)=2e,所以C错;
f(x)在(0,+∞)上最小值为f(1)=ae,∴ae≥1,∴a≥1e,∴D正确.
6.【答案】B
【解答】
解:因为f′x=1+lnx(x>0),
当x∈0,?1e时,f′x<0;当x∈1e,+∞时,f′x>0,
所以函数f(x)在0,?1e上单调递减,在1e,+∞上单调递增,
所以x=1e是函数的极小值点,也是唯一的最小值点,即最小值为f1e=?1e,
所以函数f(x)的值域为?1e,?+∞,函数的图像如下:
故A错误,B正确,C错误;
设切点为x0,??x0lnx0,则k=f′x0=1+lnx0,
所以切线方程为:y?x0lnx0=1+lnx0x?x0,
又因为切线过点(1,0),
所以0?x0lnx0=1+lnx01?x0,解得x0=1,
所以切点为(1,0),即过(1,0)点的切线有一条,故D错误.
故选B.
7.【答案】B
【解答】解:f(x)=12x?sinx,x∈(0,π),
由f′(x)=12?cosx=0,得x=π3,
当x∈(0,π3)时,f′(x)<0,f(x)单调递减,当x∈(π3,π)时,f′(x)>0,f(x)单调递增,
则f(x)在x=π3处取得极小值.
又f(x)在(0,π)上只有一个极值点,
易知f(π3)=12×π3?32=π?336即为f(x)的最小值.
8.【答案】A
【解答】
解:∵f(x)=exx+k(lnx?x),
∴f′x=x?1exx2+k1x?1
=x?1ex?kxx2,
∴x=1是函数f(x)的唯一极值点,
∴ex?kx=0在x∈0,+∞上无解,或有唯一解x=1,
①当x=1为其唯一解时,k=e,令?(x)=ex?ex(x>0),?′(x)=ex?e,
当x∈0,1时,?′x<0,即?(x)的单调递减区间为0,1,
当x∈1,+∞时,?′x>0,即?x的单调递增区间为1,+∞,
∴?x在x=1处,取得极小值,
∴k=e时,x=1是f(x)的唯一极值点;
②当k=exx在x∈0,+∞上无解,
设gx=exx
则g′x=exx?1x2,
当x∈0,1时,g′x<0,即g(x)的单调递减区间为0,1,
当x∈1,+∞时,g′x>0,即gx的单调递增区间为1,+∞,
∴gx在x=1处,取得极小值,也是其最小值,gxmin=g1=e,
又k=exx在x∈0,+∞上无解,
∴k综上k≤e.
9.【答案】B
【解答】
解:因为f′x=1+lnx(x>0),
当x∈0,?1e时,f′x<0;当x∈1e,+∞时,f′x>0,
所以函数f(x)在0,?1e上单调递减,在1e,+∞上单调递增,
所以x=1e是函数的极小值点,也是唯一的最小值点,即最小值为f1e=?1e,
所以函数f(x)的值域为?1e,?+∞,函数的图像如下:
故A错误,B正确,C错误;
设切点为x0,??x0lnx0,则k=f′x0=1+lnx0,
所以切线方程为:y?x0lnx0=1+lnx0x?x0,
又因为切线过点(1,0),
所以0?x0lnx0=1+lnx01?x0,解得x0=1,
所以切点为(1,0),即过(1,0)点的切线有一条,故D错误.
10.【答案】A
【解答】
解:f′(x)=2ax+b?1x,
由题意可知,f(x)在x=1处取得最小值,即x=1是f(x)的极值点;
∴f′(1)=0,
∴2a+b=1,即b=1?2a;
令g(x)=2?4x+lnx(x>0),
则g′(x)=1?4xx;
∴当00,g(x)在(0,14)上单调递增;
当x>14时,g′(x)<0,g(x)在(14,+∞)上单调递减;
∴g(x)≤g(14)=1+ln14=1?ln4<0;
∴g(a)<0,
即2?4a+lna=lna+2b<0;
故lna11.【答案】A
【解答】
解:∵f′(x)=x2+2ax?2,函数f(x)=13x3+ax2?2x+1在x∈(1,2)内存在极值点,
即x2+2ax?2=0在(1,2)内有解,2a=2x?x内有解,
因为y=2x?x在(1,2)为减函数,所以2x?x∈(?1,1),
即a∈(?12,12).
12.【答案】B
【解答】
解:函数f(x)=ln|x|+|sinx|(?π≤x≤π且x≠0)是偶函数,故排除A.
当x>0时,f(x)=lnx+sinx,
得f′(x)=1x+cosx,令1x+cosx=0,
作出y=1x与y=?cosx图象如图:
可知两个函数有一个交点,就是函数f(x)在(0,π]上有一个极值点,故排除D.
f(π)=lnπ>1,故排除C.
故选B.
13.【答案】
【解答】
解:∵f(x)=12ax2+xln?x?x,其中x>0,
则f′x=ax+lnx,
因为函数f(x)=12ax2+xlnx?x存在单调递增区间,
则?x>0,使得f′x>0,
即?x>0,a>?lnxx,
构造函数gx=?lnxx,x>0,
则a>gxmin,
g′x=lnx?1x2,令g′x=0,得x=e;
当0当x>e时,g′x>0,gx单调递增;
所以,函数gx在x=e处取得极小值,亦即最小值,
则gxmin=ge=?1e,
所以,a>?1e,
故答案为:.
14.【答案】②
15.【答案】(0,1]
【解答】解:不等式(2x?y)?(lny?lnx+1)≤xa对x、y>0恒成立,
可得(2?yx)?(lnyx+1)≤1a,
可设t=yx(t>0),可得f′(t)=(2?t)(lnt+1),
f′(t)=?(lnt+1)+2?tt=?lnt+2t?2,
由y=?lnt和y=2t?2在t>0递减,可得f′(t)在t>0递减,
则f′(1)=0,当t>1时,f′(t)0f′1=0,f(t)递增,
可得f(t)在t=1处取得极大值,且为最大值f(1)=1,
则1≤1a,即a?1a≤0,解得0故答案为:(0,1].
16.【答案】?52;(?∞,?1)∪(2,+∞)
【解答】
解:∵f(x)=x3+ax2+bx+c,
∴f′(x)=3x2+2ax+b,
由题意得:f′(?23)=0f′(1)=0,
解得a=?12b=?2,
所以a+b=?52;
因为f′(x)=3x2?x?2=(3x+2)(x?1),函数f(x)的单调区间如下表:
x
(?∞,?23)
?23
(?23,1)
1
(1,+∞)
f′(x)
+
0
?
0
+
f(x)
↑
极大值
↓
极小值
↑
所以函数f(x)的递增区间是(?∞,?23)和(1,+∞),递减区间是(?23,1),
当x=?23时,f(x)=2227+c为极大值,而f(2)=2+c,
所以f(2)=2+c为最大值.
要使f(x)f(2)=2+c.
解得c2;
故答案为?52;(?∞,?1)∪(2,+∞).
17.【答案】334
【解析】解:由题意可得:f′(x)=cosx+cos2x=2cos2x+cosx?1=(2cosx?1)(cosx+1),
∵cosx+1≥0,
∴当cosx>12时,f′(x)>0,
当?1即当2kπ?π3≤x≤2kπ+π3,k∈Z时,f(x)单调递增,
当2kπ+π3故f(x)在x=2kπ+π3,k∈Z处取得极大值即最大值,
且f(x)max=sinπ3+12sin(2×π3)=32+12×32=334.
故答案为:334.
对函数求导,分类讨论确定函数的单调性,求得函数的极大值点即可得解.
本题主要考查了函数的导数与极值的关系,考查极值点,属于综合题.
18.【答案】2
19.【答案】解:(1)由题意可设每天多卖出的件数为k(x2+x),
∴36=k(32+3),
∴k=3.
又每件商品的利润为(20?9?x)元,每天卖出的商品件数为69+3(x2+x).
∴该商品一天的销售利润为
f(x)=(11?x)[69+3(x2+x)]
=?3x3+30x2?36x+759(0≤x≤11).
(2)由f′(x)=?9x2+60x?36=?3(3x?2)(x?6).
令f′(x)=0可得x=23或x=6.
当x变化时,f′(x)、f(x)的变化情况如下表:
∴当商品售价为14元时,一天销售利润最大,最大值为975元.
20.【答案】解:(1)因为f′(x)=3x2+2bx+1,且Δ=4b2?12,
当?3≤b≤3时,f′(x)≥0恒成立,所以f(x)在R上单调递增,
当b3时,由f′(x)=0得x1=?b?b2?33x2=?b+b2?33,
x
(?∞,x1)
x1
(x1,x2)
x2
(x2,+∞)
f′(x)
+
0
?
0
+
f(x)
↗
极大值
↘
极小值
↗
所以f(x)在(?∞,x1)与(x2,+∞)上是单调递增的,在(x1,x2)上是单调递减的.
综上所述,
当|b|>3时,f(x)在(?∞,x1)与(x2,+∞)上单调递增,在(x1,x2)上单调递减;
当|b|≤3时,f(x)在R上单调递增.
(2)由f′(x)=3x2+2bx+c,
知x1+x2=?2b3,x1x2=c3,又|x1?x2|=2,
所以(x1?x2)2=(x1+x2)2?4x1x2=4b29?4c3=4,即c=b23?3,
所以f(1)=b+c+1=b23+b?2=13(b+32)2?114≥?114,
所以当b=?32时,c=?94,△=4b2?12c=4(b2?3c)>0,f(1)=?114,
故当b=?32,c=?94时,f(1)的最小值为?114.
一、单选题
已知函数f(x)=?x3+ax2?4在x=2处取得极值,若m∈[?1,1],则f(m)的最小值为(??? )
A. ?4 B. ?2 C. 0 D. 2
若函数fx=x3?3x在a,6?a2上有最小值,则实数a的取值范围为(??? ).
A. ?5,1 B. ?5,1 C. [?2,1) D. ?5,?2
设函数fx=x2?3ex,则(??? )
A. fx有极大值且为最大值
B. fx有极小值,但无最小值
C. 若方程fx=b恰有3个实根,则0
已知函数f(x)=13x3?4x+4在区间(2a?5,a2)上存在最大值,则实数a的取值范围是(? ?)
A. ?2,32 B. (?2,2) C. [?2,2] D. ?2,32
已知函数f(x)=aexx(a>0),下面描述正确的是
A. f(x)在R上单调递增
B. f(x)无极值点
C. 当a=2时,函数f(x)在[1,2]上有最小值e
D. 若f(x)≥1对任意x∈(0,+∞)恒成立,则a≥1e
函数f(x)=xln?x,正确的命题是(????)
A. 值域为R B. 在(1,+∞)是增函数
C. f(x)有两个不同的零点 D. 过(1,0)点的切线有两条
已知函数f(x)=12x?sinx,x∈(0,π),则f(x)的最小值为(????)
A. π6 B. π?336 C. π+336 D. 32
已知函数fx=exx+klnx?x,若x=1是函数f(x)的唯一极值点,则实数k的取值范围是(????)
A. (?∞,e] B. (?∞,e) C. (?e,+∞) D. [?e,+∞)
函数f(x)=xln?x,正确的命题是(????)
A. 值域为R B. 在(1,+∞)是增函数
C. f(x)有两个不同的零点 D. 过(1,0)点的切线有两条
已知函数fx=ax2+bx?lnx(a>0,b∈R),若对任意x>0,有fx≥f1,则(??? )
A. lna?2b C. lna=?2b D. lna≥?2b
函数f(x)=13x3+ax2?2x+1在x∈(1,2)内存在极值点,则(????)
A. ?12
函数f(x)=ln|x|+|sinx|(?π≤x≤π且x≠0)的图象大致是(????)
A. B.
C. D.
二、单空题
若函数fx=12ax2+xlnx?x存在单调递增区间,则a的取值范围是??????????.
已知函数f(x)的定义域为?1,5,部分对应值如下表.f(x)的导函数y=f′(x)的图象如图所示.
x
?1
0
4
5
f(x)
1
2
2
1
下列关于函数f(x)的命题:
①函数y=f(x)是周期函数;??? ②函数f(x)在0,2上是减函数;
③如果当x∈?1,t时,f(x)的最大值是2,那么t的最大值为4;
④当1
若对任意正实数x,y,不等式(2x?y)?(lny?lnx+1)≤xa恒成立,则实数a的取值范围a为__________
已知函数f(x)=x3+ax2+bx+c在x=?23与x=1处都取得极值,则a+b=_________.若对x∈[?1,2],不等式f(x)
设函数fx=lnx+k+1,gx=ex.若fx1=gx2,且x1?x2的最小值为?1,则实数k的值是? ? ? ? ??
三、解答题
某种商品每件进价9元,售价20元,每天可卖出69件.若售价降低,销售量可以增加,且售价降低x(0≤x≤11)元时,每天多卖出的件数与x2+x成正比.已知商品售价降低3元时,一天可多卖出36件.
(1)试将该商品一天的销售利润表示成x的函数;
(2)该商品售价为多少元时一天的销售利润最大?
已知函数f(x)=x3+bx2+cx,(b,c∈R)
(1)当c=1时,讨论函数f(x)单调性;
(2)设x1,x2是函数f(x)的两个极值点,当|x1?x2|=2时,求f(1)的最小值.
答案和解析
1.【答案】A
【解答】
解:f′(x)=?3x2+2ax,因为f(x)在x=2处取得极值,所以f′(2)=0,即?12+4a=0,所以a=3,
?则f′(x)=?3x2+6x=3x(?x+2),当?1
所以当m∈?1,1,则fm的最小值为f(0)=?4.
2.【答案】C
【解析】解:由f(x)=x3?3x,得f′(x)=3x2?3.
令f′(x)=3x2?3=0,可得x=±1.
x∈(?∞,?1)时,f′(x)>0;x∈(?1,1)时,f′(x)<0;
x∈(1,+∞)时,f′(x)>0,
∴f(x)的增区间是(?∞,?1),(1,+∞),减区间是(?1,1),
x=1为函数的极小值点,x=?1为函数的极大值点.
∵函数?f(x)在区间(a,6?a2)上有最小值,
所以函数f(x)的极小值点必在区间(a,6?a2)内,则a<1<6?a2f(a)=a3?3a≥f(1)=?2,
解得:?2≤a<1,
∴实数a的取值范围是[?2,1),
3.【答案】C
【解答】
解:∵f(x)=(x2?3)ex,∴f′(x)=2xex+(x2?3)ex=(x+3)(x?1)ex,
∴当x∈(?∞,?3)∪(1,+∞)时,f′(x)>0,函数f(x)单调递增;
当x∈(?3,1)时,f′(x)<0,函数f(x)单调递减;
∵当x∈(?∞,?3)时,x2?3>0,ex>0,∴f(x)>0,
再由f(?3)=6e3
由图象可知,f(?3)为函数的极大值但不是最大值,故A错误;
f(1)为函数的极小值,且为最小值,故B错误;
若要使f(x)=b有3个实根,
则要使函数y=b的图象与函数f(x)的图象有3个交点,
则0
则要使函数y=b的图象与函数f(x)的图象仅有1个交点,
则b>6e3或b=?2e,故D错误.
4.【答案】D
解:f′x=x2?4,令f′x=0,则x=±2,
则当x0,函数单调递增;
当?2
所以x=?2时,函数f(x)取得极大值283,
且当x=4时,f(4)=283,
要使函数f(x)=13x3?4x+4在区间(2a?5,a2)上存在最大值,
则必有:2a?55.【答案】D
【解答】
解:∵f′(x)=aex(x?1)x2,
令f′x>0得x>1,令f′x<0得x<0或0
f(x)有极小值f(1)=ae,无极大值,所以B错;
当a=2时,f(x)在[1,2]上单调递增,所以f(x)min=f(1)=2e,所以C错;
f(x)在(0,+∞)上最小值为f(1)=ae,∴ae≥1,∴a≥1e,∴D正确.
6.【答案】B
【解答】
解:因为f′x=1+lnx(x>0),
当x∈0,?1e时,f′x<0;当x∈1e,+∞时,f′x>0,
所以函数f(x)在0,?1e上单调递减,在1e,+∞上单调递增,
所以x=1e是函数的极小值点,也是唯一的最小值点,即最小值为f1e=?1e,
所以函数f(x)的值域为?1e,?+∞,函数的图像如下:
故A错误,B正确,C错误;
设切点为x0,??x0lnx0,则k=f′x0=1+lnx0,
所以切线方程为:y?x0lnx0=1+lnx0x?x0,
又因为切线过点(1,0),
所以0?x0lnx0=1+lnx01?x0,解得x0=1,
所以切点为(1,0),即过(1,0)点的切线有一条,故D错误.
故选B.
7.【答案】B
【解答】解:f(x)=12x?sinx,x∈(0,π),
由f′(x)=12?cosx=0,得x=π3,
当x∈(0,π3)时,f′(x)<0,f(x)单调递减,当x∈(π3,π)时,f′(x)>0,f(x)单调递增,
则f(x)在x=π3处取得极小值.
又f(x)在(0,π)上只有一个极值点,
易知f(π3)=12×π3?32=π?336即为f(x)的最小值.
8.【答案】A
【解答】
解:∵f(x)=exx+k(lnx?x),
∴f′x=x?1exx2+k1x?1
=x?1ex?kxx2,
∴x=1是函数f(x)的唯一极值点,
∴ex?kx=0在x∈0,+∞上无解,或有唯一解x=1,
①当x=1为其唯一解时,k=e,令?(x)=ex?ex(x>0),?′(x)=ex?e,
当x∈0,1时,?′x<0,即?(x)的单调递减区间为0,1,
当x∈1,+∞时,?′x>0,即?x的单调递增区间为1,+∞,
∴?x在x=1处,取得极小值,
∴k=e时,x=1是f(x)的唯一极值点;
②当k=exx在x∈0,+∞上无解,
设gx=exx
则g′x=exx?1x2,
当x∈0,1时,g′x<0,即g(x)的单调递减区间为0,1,
当x∈1,+∞时,g′x>0,即gx的单调递增区间为1,+∞,
∴gx在x=1处,取得极小值,也是其最小值,gxmin=g1=e,
又k=exx在x∈0,+∞上无解,
∴k
9.【答案】B
【解答】
解:因为f′x=1+lnx(x>0),
当x∈0,?1e时,f′x<0;当x∈1e,+∞时,f′x>0,
所以函数f(x)在0,?1e上单调递减,在1e,+∞上单调递增,
所以x=1e是函数的极小值点,也是唯一的最小值点,即最小值为f1e=?1e,
所以函数f(x)的值域为?1e,?+∞,函数的图像如下:
故A错误,B正确,C错误;
设切点为x0,??x0lnx0,则k=f′x0=1+lnx0,
所以切线方程为:y?x0lnx0=1+lnx0x?x0,
又因为切线过点(1,0),
所以0?x0lnx0=1+lnx01?x0,解得x0=1,
所以切点为(1,0),即过(1,0)点的切线有一条,故D错误.
10.【答案】A
【解答】
解:f′(x)=2ax+b?1x,
由题意可知,f(x)在x=1处取得最小值,即x=1是f(x)的极值点;
∴f′(1)=0,
∴2a+b=1,即b=1?2a;
令g(x)=2?4x+lnx(x>0),
则g′(x)=1?4xx;
∴当0
当x>14时,g′(x)<0,g(x)在(14,+∞)上单调递减;
∴g(x)≤g(14)=1+ln14=1?ln4<0;
∴g(a)<0,
即2?4a+lna=lna+2b<0;
故lna11.【答案】A
【解答】
解:∵f′(x)=x2+2ax?2,函数f(x)=13x3+ax2?2x+1在x∈(1,2)内存在极值点,
即x2+2ax?2=0在(1,2)内有解,2a=2x?x内有解,
因为y=2x?x在(1,2)为减函数,所以2x?x∈(?1,1),
即a∈(?12,12).
12.【答案】B
【解答】
解:函数f(x)=ln|x|+|sinx|(?π≤x≤π且x≠0)是偶函数,故排除A.
当x>0时,f(x)=lnx+sinx,
得f′(x)=1x+cosx,令1x+cosx=0,
作出y=1x与y=?cosx图象如图:
可知两个函数有一个交点,就是函数f(x)在(0,π]上有一个极值点,故排除D.
f(π)=lnπ>1,故排除C.
故选B.
13.【答案】
【解答】
解:∵f(x)=12ax2+xln?x?x,其中x>0,
则f′x=ax+lnx,
因为函数f(x)=12ax2+xlnx?x存在单调递增区间,
则?x>0,使得f′x>0,
即?x>0,a>?lnxx,
构造函数gx=?lnxx,x>0,
则a>gxmin,
g′x=lnx?1x2,令g′x=0,得x=e;
当0
所以,函数gx在x=e处取得极小值,亦即最小值,
则gxmin=ge=?1e,
所以,a>?1e,
故答案为:.
14.【答案】②
15.【答案】(0,1]
【解答】解:不等式(2x?y)?(lny?lnx+1)≤xa对x、y>0恒成立,
可得(2?yx)?(lnyx+1)≤1a,
可设t=yx(t>0),可得f′(t)=(2?t)(lnt+1),
f′(t)=?(lnt+1)+2?tt=?lnt+2t?2,
由y=?lnt和y=2t?2在t>0递减,可得f′(t)在t>0递减,
则f′(1)=0,当t>1时,f′(t)
可得f(t)在t=1处取得极大值,且为最大值f(1)=1,
则1≤1a,即a?1a≤0,解得0
16.【答案】?52;(?∞,?1)∪(2,+∞)
【解答】
解:∵f(x)=x3+ax2+bx+c,
∴f′(x)=3x2+2ax+b,
由题意得:f′(?23)=0f′(1)=0,
解得a=?12b=?2,
所以a+b=?52;
因为f′(x)=3x2?x?2=(3x+2)(x?1),函数f(x)的单调区间如下表:
x
(?∞,?23)
?23
(?23,1)
1
(1,+∞)
f′(x)
+
0
?
0
+
f(x)
↑
极大值
↓
极小值
↑
所以函数f(x)的递增区间是(?∞,?23)和(1,+∞),递减区间是(?23,1),
当x=?23时,f(x)=2227+c为极大值,而f(2)=2+c,
所以f(2)=2+c为最大值.
要使f(x)
解得c2;
故答案为?52;(?∞,?1)∪(2,+∞).
17.【答案】334
【解析】解:由题意可得:f′(x)=cosx+cos2x=2cos2x+cosx?1=(2cosx?1)(cosx+1),
∵cosx+1≥0,
∴当cosx>12时,f′(x)>0,
当?1
当2kπ+π3
且f(x)max=sinπ3+12sin(2×π3)=32+12×32=334.
故答案为:334.
对函数求导,分类讨论确定函数的单调性,求得函数的极大值点即可得解.
本题主要考查了函数的导数与极值的关系,考查极值点,属于综合题.
18.【答案】2
19.【答案】解:(1)由题意可设每天多卖出的件数为k(x2+x),
∴36=k(32+3),
∴k=3.
又每件商品的利润为(20?9?x)元,每天卖出的商品件数为69+3(x2+x).
∴该商品一天的销售利润为
f(x)=(11?x)[69+3(x2+x)]
=?3x3+30x2?36x+759(0≤x≤11).
(2)由f′(x)=?9x2+60x?36=?3(3x?2)(x?6).
令f′(x)=0可得x=23或x=6.
当x变化时,f′(x)、f(x)的变化情况如下表:
∴当商品售价为14元时,一天销售利润最大,最大值为975元.
20.【答案】解:(1)因为f′(x)=3x2+2bx+1,且Δ=4b2?12,
当?3≤b≤3时,f′(x)≥0恒成立,所以f(x)在R上单调递增,
当b3时,由f′(x)=0得x1=?b?b2?33x2=?b+b2?33,
x
(?∞,x1)
x1
(x1,x2)
x2
(x2,+∞)
f′(x)
+
0
?
0
+
f(x)
↗
极大值
↘
极小值
↗
所以f(x)在(?∞,x1)与(x2,+∞)上是单调递增的,在(x1,x2)上是单调递减的.
综上所述,
当|b|>3时,f(x)在(?∞,x1)与(x2,+∞)上单调递增,在(x1,x2)上单调递减;
当|b|≤3时,f(x)在R上单调递增.
(2)由f′(x)=3x2+2bx+c,
知x1+x2=?2b3,x1x2=c3,又|x1?x2|=2,
所以(x1?x2)2=(x1+x2)2?4x1x2=4b29?4c3=4,即c=b23?3,
所以f(1)=b+c+1=b23+b?2=13(b+32)2?114≥?114,
所以当b=?32时,c=?94,△=4b2?12c=4(b2?3c)>0,f(1)=?114,
故当b=?32,c=?94时,f(1)的最小值为?114.
