2010年黑龙江中考数学试卷第28题一题多解
图片预览



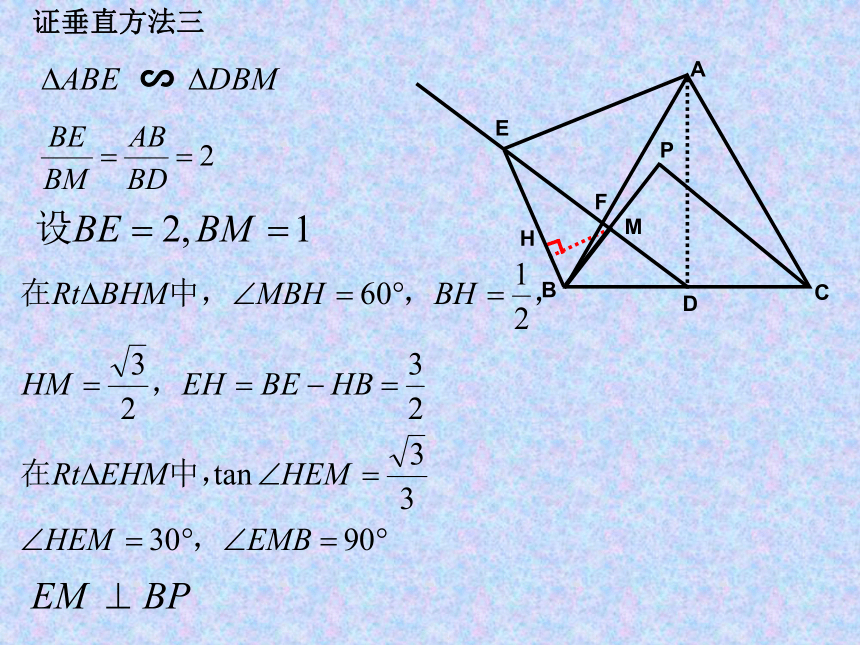
文档简介
(共30张PPT)
2010年中考第28题
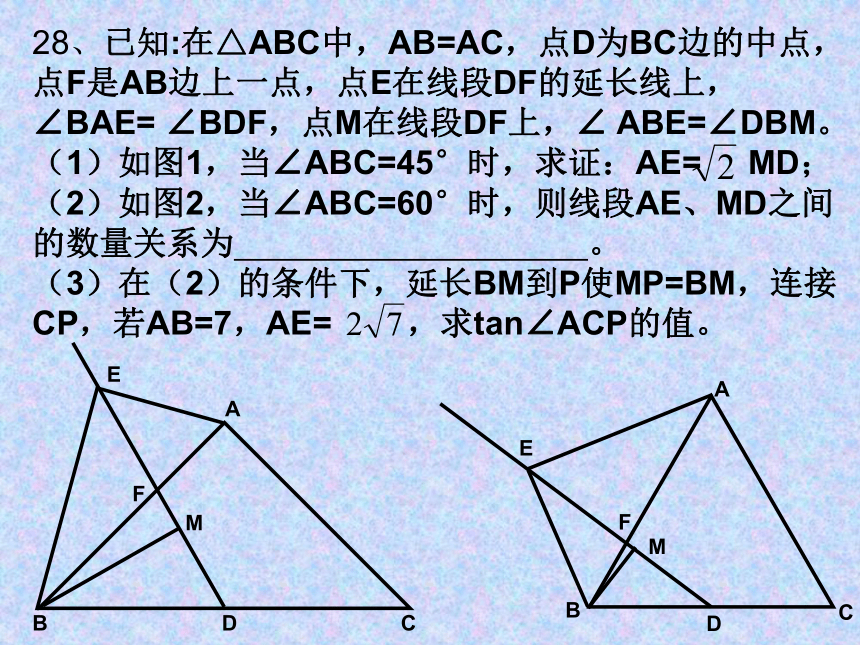
28、已知:在△ABC中,AB=AC,点D为BC边的中点,点F是AB边上一点,点E在线段DF的延长线上,∠BAE= ∠BDF,点M在线段DF上,∠ ABE=∠DBM。
(1)如图1,当∠ABC=45°时,求证:AE= MD;
(2)如图2,当∠ABC=60°时,则线段AE、MD之间的数量关系为 。
(3)在(2)的条件下,延长BM到P使MP=BM,连接CP,若AB=7,AE= ,求tan∠ACP的值。
A
B
C
D
M
F
E
C
A
B
E
F
D
M
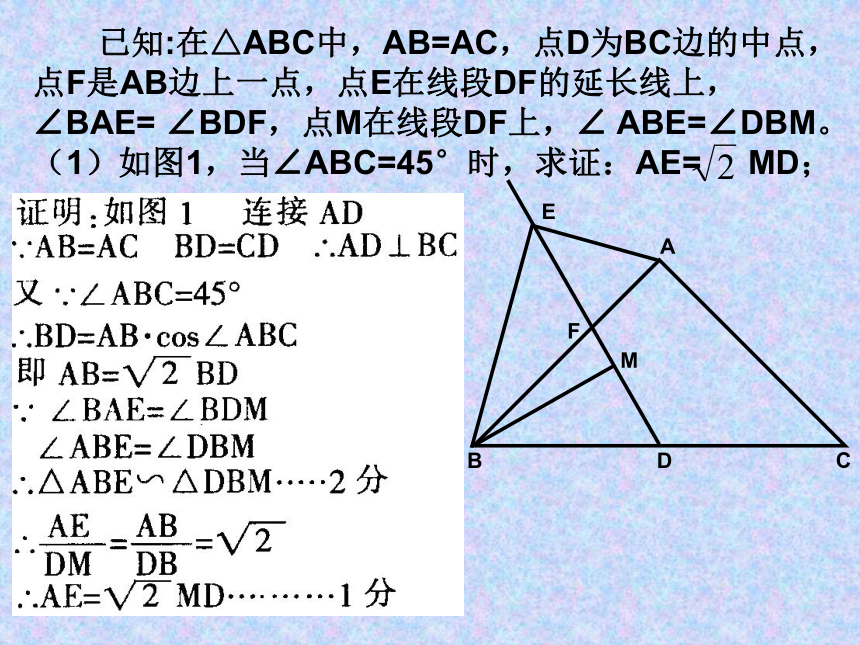
已知:在△ABC中,AB=AC,点D为BC边的中点,点F是AB边上一点,点E在线段DF的延长线上,∠BAE= ∠BDF,点M在线段DF上,∠ ABE=∠DBM。
(1)如图1,当∠ABC=45°时,求证:AE= MD;
A
B
C
D
M
F
E
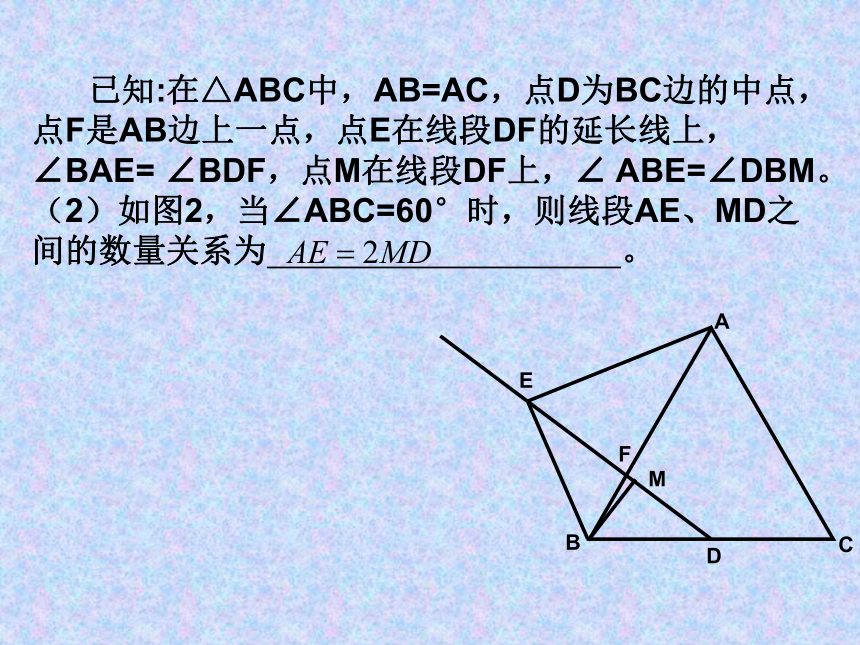
已知:在△ABC中,AB=AC,点D为BC边的中点,点F是AB边上一点,点E在线段DF的延长线上,∠BAE= ∠BDF,点M在线段DF上,∠ ABE=∠DBM。
(2)如图2,当∠ABC=60°时,则线段AE、MD之间的数量关系为 。
C
A
B
E
F
D
M
H
N
P
C
A
B
E
F
D
M
评分细则
(1)问相似1分,给出一定条件得出AB与BD的关系1分,整个证明过程中有比的形式与结论1分。其余证法只要落到这三个采分点上就给分。相似写成全等,字母写错都算笔误,三处笔误扣一分。设BD=1,推出 给分,没有“设”字直接写BD=1没分
(2)问填空时与答案一致或恒等变形的式子都给分。用文字表达正确也给分。
(3)问①用到△ABE∽△DBM时必须重新证明,写同理可证或同(1)可证都扣1分,因为图形变了,必须重新证明。②证明 EM⊥BP证错的特别多,相当于默认EM⊥BP,此种情况属于关键步骤证明错误,只给结论1分。③前面有几步,结论对了给1分,直接写结论不给分④辅助线说了没画扣1分,画了没说不扣分⑤用一元二次方程求得的参数值需舍一个,没舍的扣1分。
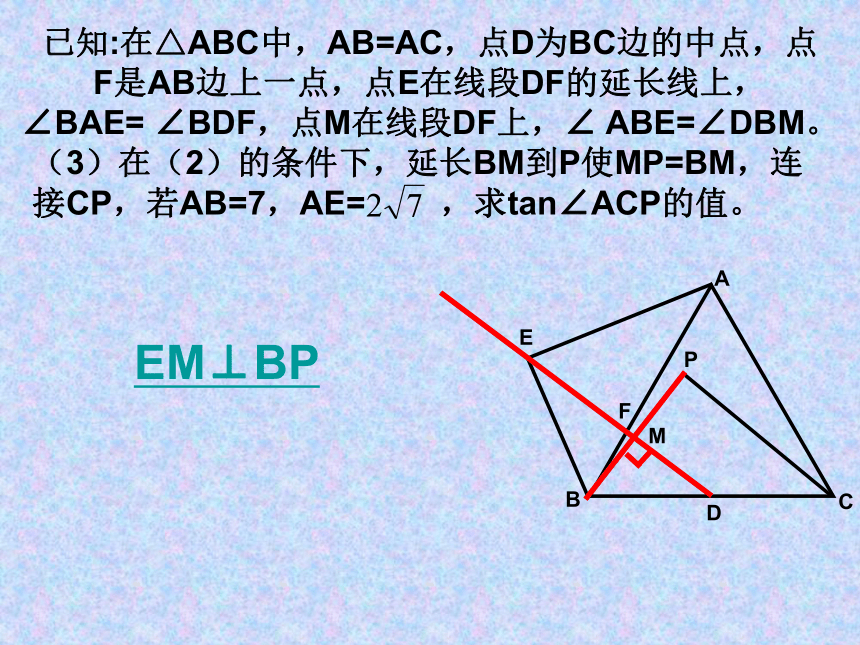
已知:在△ABC中,AB=AC,点D为BC边的中点,点F是AB边上一点,点E在线段DF的延长线上,∠BAE= ∠BDF,点M在线段DF上,∠ ABE=∠DBM。
(3)在(2)的条件下,延长BM到P使MP=BM,连接CP,若AB=7,AE= ,求tan∠ACP的值。
P
C
A
B
E
F
D
M
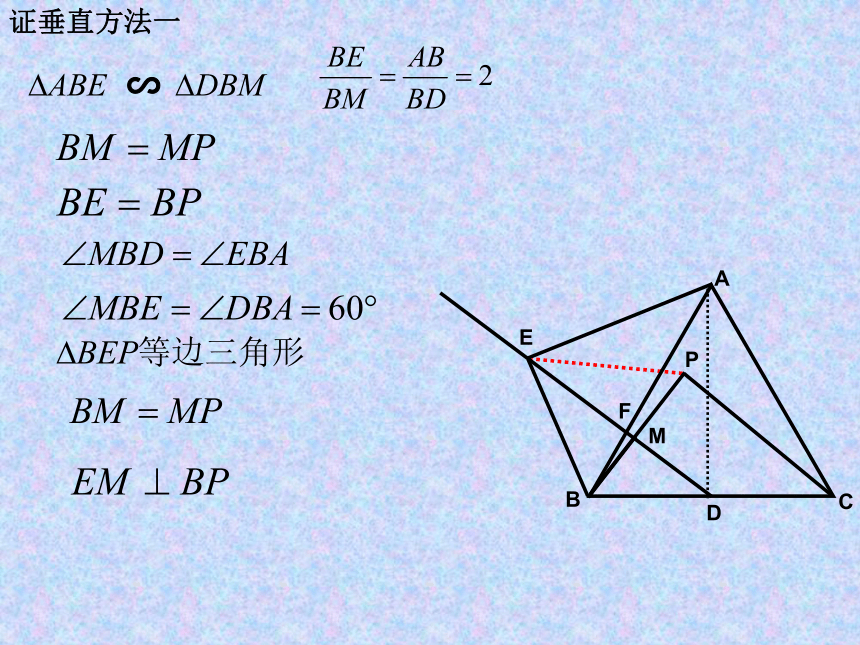
EM⊥BP
P
C
A
B
E
F
D
M
证垂直方法一
∽
P
C
A
B
E
F
D
M
G
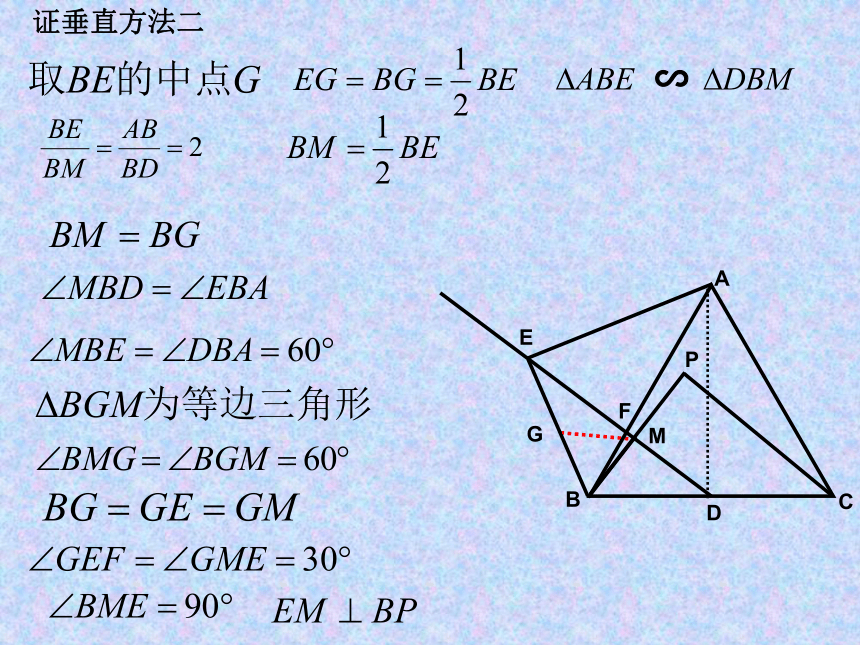
证垂直方法二
∽
P
C
A
B
E
F
D
M
H
∽
证垂直方法三
N
P
C
A
B
E
F
D
M
∽
∽
∽
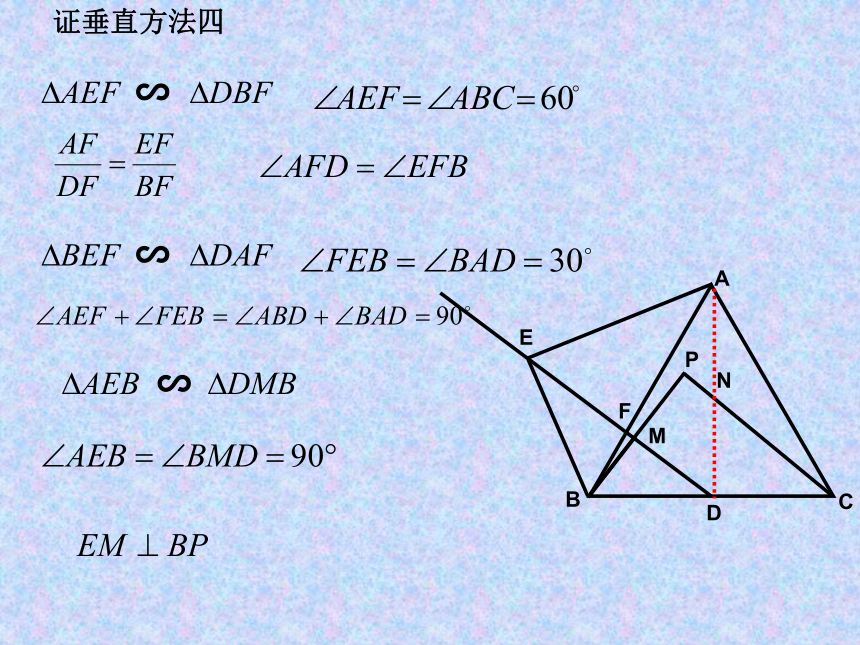
证垂直方法四
P
C
A
B
E
F
D
M
G
H
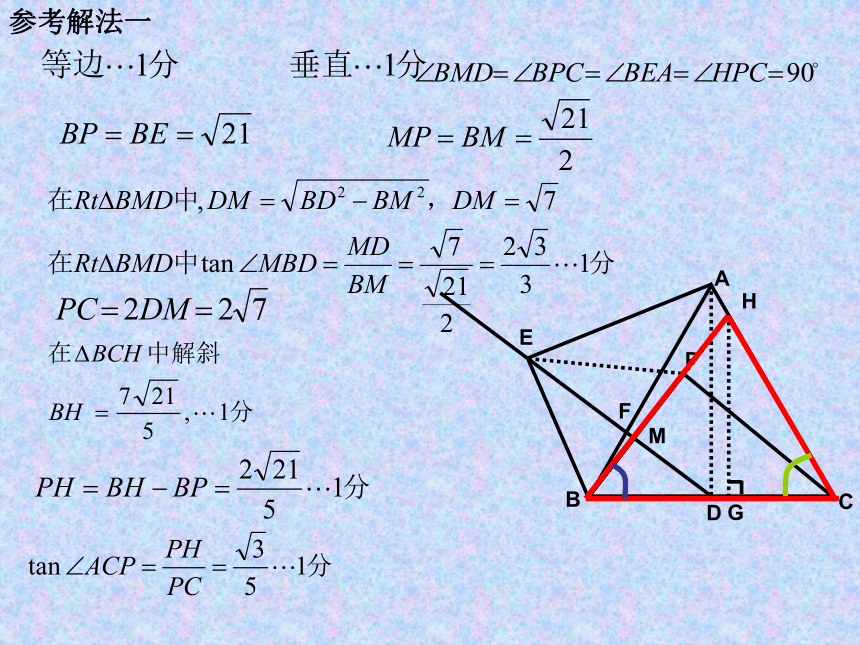
参考解法一
P
C
A
B
E
F
D
M
H
G
参考解法二
P
C
A
B
E
F
D
M
L
Q
参考解法三
∽
∽
H
P
C
A
B
E
F
D
M
G
参考解法四
P
C
A
B
E
F
D
M
N
G
H
参考解法五
P
C
A
B
E
F
D
M
N
参考解法六
∽
P
C
A
B
E
F
D
M
T
S
参考解法七
G
K
P
C
A
B
E
F
D
M
H
∽
参考解法八
主要对相似三角形的性质判定、勾股定理、等边三角形的性质判定、锐角三角函数、解直角三角形、三角形的面积公式、线段的和差、中位线的定义性质、平行线的性质、垂直的性质、一元二次方程解法及根的检验、三角形内角和定理及其推论、全等三角形的判定及性质等知识点的考查。
考查知识点
思想方法
运动变换思想
转化思想
方程思想
函数思想
分类讨论思想
… …
能力要求
28题作为探究型综合题,它是以基本图形为背景,图形变换为载体考察学生的逻辑推理能力,图形分解能力,抽象能力,迁移能力,计算能力,全面分析问题能力。
教学感受:
1、 对前两问批卷要求不是特别严格,重视方法和对知识地掌握,要从学生的角度出发,从理解学生出发。在以后教学生中,对学生的书写要求适当。
2、第三问从这次批卷来看,在中间过程不是很完整或出现一些实质性问题的情况下,如果结论正确只能得到结论的1分。有相当一部分学生在此处乱用知识或逆用定义、定理。建议对知识点的讲解要砸实尤其是逆定理是否可用。
3、从第三问的解法来看,垂直是本题的关键点。部分学生在此处没有证明出来。建议注重双基训练。
4、无论是否证垂直,几乎都应用了斜三角形可解,所以我觉得这正是今年中考的一大改变。为什么这样改,可能与原23题(锐角三角函数的考察)的消失有关。
H
N
P
C
A
B
E
F
D
M
已知:在△ABC中,AB=AC,点D为BC边的中点,点F是AB边上一点,点E在线段DF的延长线上,∠BAE= ∠BDF,点M在线段DF上,∠ ABE=∠DBM。
(3)在(2)的条件下,延长BM到P使MP=BM,连接CP,若AB=7,AE= ,求tan∠ACP的值。
已知:在△ABC中,AB=AC,点D为BC边的中点,点F是AB边上一点,点E在线段DF的延长线上,∠BAE= ∠BDF,点M在线段DF上,∠ ABE=∠DBM。
(3)在(2)的条件下,延长BM到P使MP=BM,连接CP,若AB=7,AE= ,求tan∠ACP的值。
大角可拆分为: 小角 加 小角
2010的非特殊角三角函数的应用。
2008年的动点,
2009年的半角旋转,
谢谢!
已知:在△ABC中,AB=AC,点D为BC边的中点,点F是AB边上一点,点E在线段DF的延长线上,∠BAE= ∠BDF,点M在线段DF上,∠ ABE=∠DBM。
(3)在(2)的条件下,延长BM到P使MP=BM,连接CP,若AB=7,AE= ,求tan∠ACP的值。
H
N
P
C
A
B
E
F
D
M
K
G
2010年中考第28题
28、已知:在△ABC中,AB=AC,点D为BC边的中点,点F是AB边上一点,点E在线段DF的延长线上,∠BAE= ∠BDF,点M在线段DF上,∠ ABE=∠DBM。
(1)如图1,当∠ABC=45°时,求证:AE= MD;
(2)如图2,当∠ABC=60°时,则线段AE、MD之间的数量关系为 。
(3)在(2)的条件下,延长BM到P使MP=BM,连接CP,若AB=7,AE= ,求tan∠ACP的值。
A
B
C
D
M
F
E
C
A
B
E
F
D
M
已知:在△ABC中,AB=AC,点D为BC边的中点,点F是AB边上一点,点E在线段DF的延长线上,∠BAE= ∠BDF,点M在线段DF上,∠ ABE=∠DBM。
(1)如图1,当∠ABC=45°时,求证:AE= MD;
A
B
C
D
M
F
E
已知:在△ABC中,AB=AC,点D为BC边的中点,点F是AB边上一点,点E在线段DF的延长线上,∠BAE= ∠BDF,点M在线段DF上,∠ ABE=∠DBM。
(2)如图2,当∠ABC=60°时,则线段AE、MD之间的数量关系为 。
C
A
B
E
F
D
M
H
N
P
C
A
B
E
F
D
M
评分细则
(1)问相似1分,给出一定条件得出AB与BD的关系1分,整个证明过程中有比的形式与结论1分。其余证法只要落到这三个采分点上就给分。相似写成全等,字母写错都算笔误,三处笔误扣一分。设BD=1,推出 给分,没有“设”字直接写BD=1没分
(2)问填空时与答案一致或恒等变形的式子都给分。用文字表达正确也给分。
(3)问①用到△ABE∽△DBM时必须重新证明,写同理可证或同(1)可证都扣1分,因为图形变了,必须重新证明。②证明 EM⊥BP证错的特别多,相当于默认EM⊥BP,此种情况属于关键步骤证明错误,只给结论1分。③前面有几步,结论对了给1分,直接写结论不给分④辅助线说了没画扣1分,画了没说不扣分⑤用一元二次方程求得的参数值需舍一个,没舍的扣1分。
已知:在△ABC中,AB=AC,点D为BC边的中点,点F是AB边上一点,点E在线段DF的延长线上,∠BAE= ∠BDF,点M在线段DF上,∠ ABE=∠DBM。
(3)在(2)的条件下,延长BM到P使MP=BM,连接CP,若AB=7,AE= ,求tan∠ACP的值。
P
C
A
B
E
F
D
M
EM⊥BP
P
C
A
B
E
F
D
M
证垂直方法一
∽
P
C
A
B
E
F
D
M
G
证垂直方法二
∽
P
C
A
B
E
F
D
M
H
∽
证垂直方法三
N
P
C
A
B
E
F
D
M
∽
∽
∽
证垂直方法四
P
C
A
B
E
F
D
M
G
H
参考解法一
P
C
A
B
E
F
D
M
H
G
参考解法二
P
C
A
B
E
F
D
M
L
Q
参考解法三
∽
∽
H
P
C
A
B
E
F
D
M
G
参考解法四
P
C
A
B
E
F
D
M
N
G
H
参考解法五
P
C
A
B
E
F
D
M
N
参考解法六
∽
P
C
A
B
E
F
D
M
T
S
参考解法七
G
K
P
C
A
B
E
F
D
M
H
∽
参考解法八
主要对相似三角形的性质判定、勾股定理、等边三角形的性质判定、锐角三角函数、解直角三角形、三角形的面积公式、线段的和差、中位线的定义性质、平行线的性质、垂直的性质、一元二次方程解法及根的检验、三角形内角和定理及其推论、全等三角形的判定及性质等知识点的考查。
考查知识点
思想方法
运动变换思想
转化思想
方程思想
函数思想
分类讨论思想
… …
能力要求
28题作为探究型综合题,它是以基本图形为背景,图形变换为载体考察学生的逻辑推理能力,图形分解能力,抽象能力,迁移能力,计算能力,全面分析问题能力。
教学感受:
1、 对前两问批卷要求不是特别严格,重视方法和对知识地掌握,要从学生的角度出发,从理解学生出发。在以后教学生中,对学生的书写要求适当。
2、第三问从这次批卷来看,在中间过程不是很完整或出现一些实质性问题的情况下,如果结论正确只能得到结论的1分。有相当一部分学生在此处乱用知识或逆用定义、定理。建议对知识点的讲解要砸实尤其是逆定理是否可用。
3、从第三问的解法来看,垂直是本题的关键点。部分学生在此处没有证明出来。建议注重双基训练。
4、无论是否证垂直,几乎都应用了斜三角形可解,所以我觉得这正是今年中考的一大改变。为什么这样改,可能与原23题(锐角三角函数的考察)的消失有关。
H
N
P
C
A
B
E
F
D
M
已知:在△ABC中,AB=AC,点D为BC边的中点,点F是AB边上一点,点E在线段DF的延长线上,∠BAE= ∠BDF,点M在线段DF上,∠ ABE=∠DBM。
(3)在(2)的条件下,延长BM到P使MP=BM,连接CP,若AB=7,AE= ,求tan∠ACP的值。
已知:在△ABC中,AB=AC,点D为BC边的中点,点F是AB边上一点,点E在线段DF的延长线上,∠BAE= ∠BDF,点M在线段DF上,∠ ABE=∠DBM。
(3)在(2)的条件下,延长BM到P使MP=BM,连接CP,若AB=7,AE= ,求tan∠ACP的值。
大角可拆分为: 小角 加 小角
2010的非特殊角三角函数的应用。
2008年的动点,
2009年的半角旋转,
谢谢!
已知:在△ABC中,AB=AC,点D为BC边的中点,点F是AB边上一点,点E在线段DF的延长线上,∠BAE= ∠BDF,点M在线段DF上,∠ ABE=∠DBM。
(3)在(2)的条件下,延长BM到P使MP=BM,连接CP,若AB=7,AE= ,求tan∠ACP的值。
H
N
P
C
A
B
E
F
D
M
K
G
同课章节目录
