苏科版七年级下册数学课件 11.8小结与思考(共20张ppt)
文档属性
| 名称 | 苏科版七年级下册数学课件 11.8小结与思考(共20张ppt) |  | |
| 格式 | ppt | ||
| 文件大小 | 682.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-04-19 12:57:46 | ||
图片预览






文档简介
一元一次不等式(组)复习
考点一不等式及其基本性质?
1.定义
用不等号连接而成的式子.
2.性质
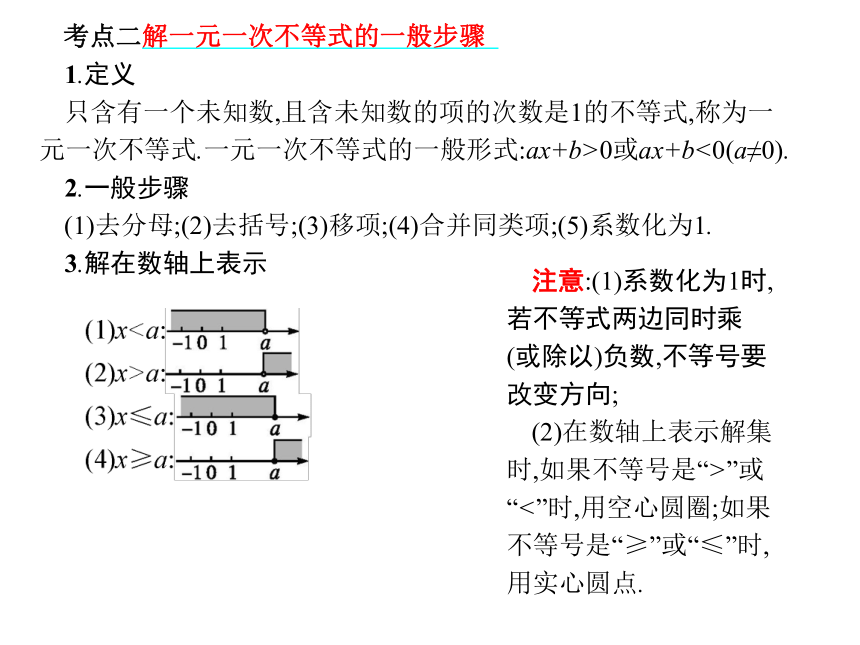
考点二解一元一次不等式的一般步骤?
1.定义
只含有一个未知数,且含未知数的项的次数是1的不等式,称为一元一次不等式.一元一次不等式的一般形式:ax+b>0或ax+b<0(a≠0).
2.一般步骤
(1)去分母;(2)去括号;(3)移项;(4)合并同类项;(5)系数化为1.
3.解在数轴上表示
注意:(1)系数化为1时,若不等式两边同时乘(或除以)负数,不等号要改变方向;
(2)在数轴上表示解集时,如果不等号是“>”或“<”时,用空心圆圈;如果不等号是“≥”或“≤”时,用实心圆点.
考点三一元一次不等式组及其解法(高频)?
1.定义
含有相同未知数的几个一元一次不等式联立起来,就组成了一个一元一次不等式组.
2.一元一次不等式组的解集
几个一元一次不等式解集的公共部分叫做由它们所组成的一元一次不等式组的解集.
3.一般步骤
(1)分别求出不等式组中各个不等式的解集;
(2)利用数轴求出这些解集的公共部分或利用下表中的口诀,即可求出不等式组的解集.
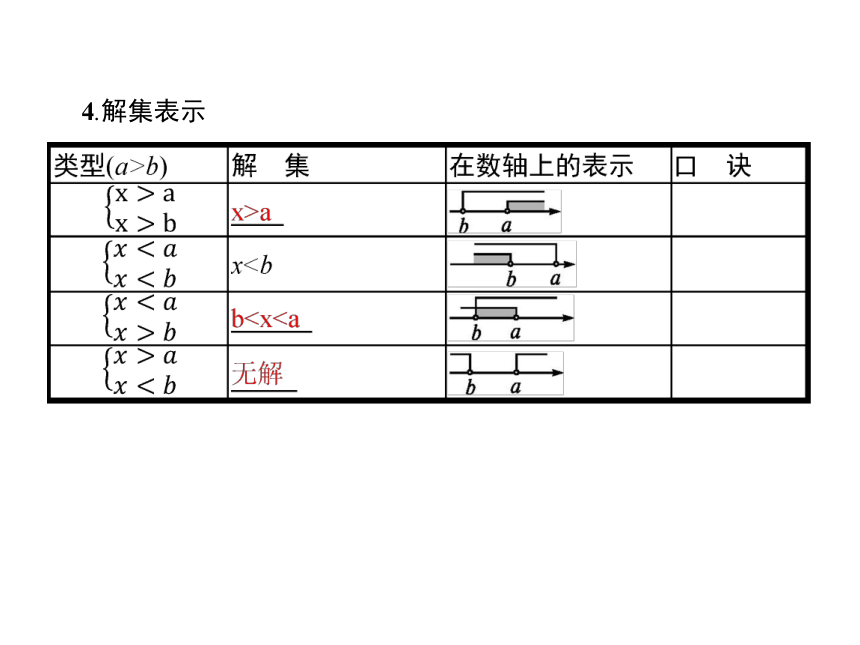
4.解集表示
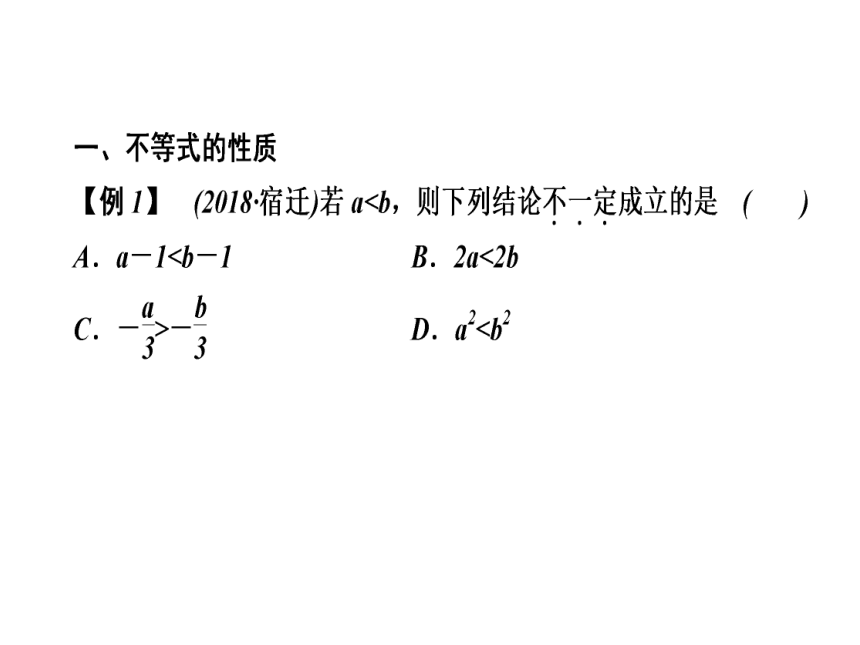
【解析】 根据不等式性质1知,A一定成立;根据不等式性质2知,B一定成立;根据不等式性质3知,C一定成立;D不一定成立,如-3<-2,但(-3)2>(-2)2.
【答案】 D
【点拨】 这类题主要考查不等式的基本性质,熟悉不等式的基本性质是解题的关键.
【解析】 解不等式,就是求出这个不等式的解集的过程.按照先去分母,再去括号,移项,合并同类项,最后将未知数的系数化为1的基本步骤求出不等式的解集.
【答案】 解:去分母,得2(x-1)≥x-2+6;
去括号,得2x-2≥x-2+6;
移项,得2x-x≥2-2+6;
合并,得x≥6.
【点拨】 解决此类不等式的关键是去分母时别忘了把常数项也乘以公分母.
【解析】 先分别求出每一个不等式的解集,再利用数轴求得这两个不等式解集的公共部分就是原不等式组的解集.
【答案】 解①得x>-4;解②得x≤2.
在数轴上表示解集:
原不等式组的解集为-4<x≤2.
【点拨】 会解每一个一元一次不等式是解不等式组的基础,能借助数轴确定不等式组的解集是基本能力,而且也有助于快捷的找到不等式组的特殊解.
【易错提醒】 在数轴上表示不等式的解集要注意方向和空、实心点问题.(1)向左表示小于,向右表示大于;(2)空心点表示不包括该点表示的数,实心点表示包括该点表示的数(即含有等于).
解:解第一个不等式得x<3,解第二个不等式得x>-1,所以原不等式组的解集为-1<x<3,在数轴上表示如下:
5.(2018·南京)如图,在数轴上,点A,B分别表示数1,-2x+3.
(1)求x的取值范围.
(2)数轴上表示数-x+2的点应落在( ).
A.点A的左边 B.线段AB上 C.点B的右边
解:(1)1<-2x+3,解得x<1.
(2)由(1)知x<1,∴-x>-1,∴-x+2>1.∵(-x+2)-(-2x+3)=x-1<0,∴-x+2<-2x+3,∴表示数-x+2的点落在线段AB上.
不等式(组)中字母的取值?
A.3 B.1 C.0 D.-3
答案:B
∵原不等式组仅有四个整数解,
∴整数解是3,2,1,0,∴-4∵分式方程有非负数解,∴a≥-2且a≠2.
∴所有满足条件的整数a有-2,-1,0,1,3,其和为1.
方法总结本题是关于不等式组的整数解的问题,应先解不等式组,根据不等式组的解集找出符合要求的整数解,再根据整数解确定a的取值范围;如不太容易确定,则可以借助数轴来解答.
(2017·黑龙江大庆)若实数3是不等式2x-a-2<0的一个解,则a可取的最小正整数为( D )
A.2 B.3 C.4 D.5
对应训练
(2017·湖北恩施)如果关于x的不等式组 无解,那么m的取值范围是( A )
A.m≤-1 B.m<-1
C.-1(2017·山东泰安)不等式组 的解集为x<2.则k的取值范围为( C )
A.k>1 B.k<1 C.k≥1 D.k≤1
本节课,你有什么收获?
考点一不等式及其基本性质?
1.定义
用不等号连接而成的式子.
2.性质
考点二解一元一次不等式的一般步骤?
1.定义
只含有一个未知数,且含未知数的项的次数是1的不等式,称为一元一次不等式.一元一次不等式的一般形式:ax+b>0或ax+b<0(a≠0).
2.一般步骤
(1)去分母;(2)去括号;(3)移项;(4)合并同类项;(5)系数化为1.
3.解在数轴上表示
注意:(1)系数化为1时,若不等式两边同时乘(或除以)负数,不等号要改变方向;
(2)在数轴上表示解集时,如果不等号是“>”或“<”时,用空心圆圈;如果不等号是“≥”或“≤”时,用实心圆点.
考点三一元一次不等式组及其解法(高频)?
1.定义
含有相同未知数的几个一元一次不等式联立起来,就组成了一个一元一次不等式组.
2.一元一次不等式组的解集
几个一元一次不等式解集的公共部分叫做由它们所组成的一元一次不等式组的解集.
3.一般步骤
(1)分别求出不等式组中各个不等式的解集;
(2)利用数轴求出这些解集的公共部分或利用下表中的口诀,即可求出不等式组的解集.
4.解集表示
【解析】 根据不等式性质1知,A一定成立;根据不等式性质2知,B一定成立;根据不等式性质3知,C一定成立;D不一定成立,如-3<-2,但(-3)2>(-2)2.
【答案】 D
【点拨】 这类题主要考查不等式的基本性质,熟悉不等式的基本性质是解题的关键.
【解析】 解不等式,就是求出这个不等式的解集的过程.按照先去分母,再去括号,移项,合并同类项,最后将未知数的系数化为1的基本步骤求出不等式的解集.
【答案】 解:去分母,得2(x-1)≥x-2+6;
去括号,得2x-2≥x-2+6;
移项,得2x-x≥2-2+6;
合并,得x≥6.
【点拨】 解决此类不等式的关键是去分母时别忘了把常数项也乘以公分母.
【解析】 先分别求出每一个不等式的解集,再利用数轴求得这两个不等式解集的公共部分就是原不等式组的解集.
【答案】 解①得x>-4;解②得x≤2.
在数轴上表示解集:
原不等式组的解集为-4<x≤2.
【点拨】 会解每一个一元一次不等式是解不等式组的基础,能借助数轴确定不等式组的解集是基本能力,而且也有助于快捷的找到不等式组的特殊解.
【易错提醒】 在数轴上表示不等式的解集要注意方向和空、实心点问题.(1)向左表示小于,向右表示大于;(2)空心点表示不包括该点表示的数,实心点表示包括该点表示的数(即含有等于).
解:解第一个不等式得x<3,解第二个不等式得x>-1,所以原不等式组的解集为-1<x<3,在数轴上表示如下:
5.(2018·南京)如图,在数轴上,点A,B分别表示数1,-2x+3.
(1)求x的取值范围.
(2)数轴上表示数-x+2的点应落在( ).
A.点A的左边 B.线段AB上 C.点B的右边
解:(1)1<-2x+3,解得x<1.
(2)由(1)知x<1,∴-x>-1,∴-x+2>1.∵(-x+2)-(-2x+3)=x-1<0,∴-x+2<-2x+3,∴表示数-x+2的点落在线段AB上.
不等式(组)中字母的取值?
A.3 B.1 C.0 D.-3
答案:B
∵原不等式组仅有四个整数解,
∴整数解是3,2,1,0,∴-4
∴所有满足条件的整数a有-2,-1,0,1,3,其和为1.
方法总结本题是关于不等式组的整数解的问题,应先解不等式组,根据不等式组的解集找出符合要求的整数解,再根据整数解确定a的取值范围;如不太容易确定,则可以借助数轴来解答.
(2017·黑龙江大庆)若实数3是不等式2x-a-2<0的一个解,则a可取的最小正整数为( D )
A.2 B.3 C.4 D.5
对应训练
(2017·湖北恩施)如果关于x的不等式组 无解,那么m的取值范围是( A )
A.m≤-1 B.m<-1
C.-1
A.k>1 B.k<1 C.k≥1 D.k≤1
本节课,你有什么收获?
同课章节目录
- 第7章 平面图形的认识(二)
- 7.1 探索直线平行的条件
- 7.2 探索平行线的性质
- 7.3 图形的平移
- 7.4 认识三角形
- 7.5 多边形的内角和与外角和
- 第8章 幂的运算
- 8.1 同底数幂的乘法
- 8.2 幂的乘方与积的乘方
- 8.3 同底数幂的除法
- 第9章 整式乘法与因式分解
- 9.1 单项式乘单项式
- 9.2 单项式乘多项式
- 9.3 多项式乘多项式
- 9.4 乘法公式
- 9.5 多项式的因式分解
- 第10章 二元一次方程组
- 10.1 二元一次方程
- 10.2 二元一次方程组
- 10.3 解二元一次方程组
- 10.4 三元一次方程组
- 10.5 用二元一次方程解决问题
- 第11章 一元一次不等式
- 11.1 生活中的不等式
- 11.2 不等式的解集
- 11.3 不等式的性质
- 11.4 解一元一次不等式
- 11.5 用一元一次不等式解决问题
- 11.6 一元一次不等式组
- 第12章 证明
- 12.1 定义与命题
- 12.2 证明
- 12.3 互逆命题
