5.2.1平行线
图片预览




文档简介
(共25张PPT)
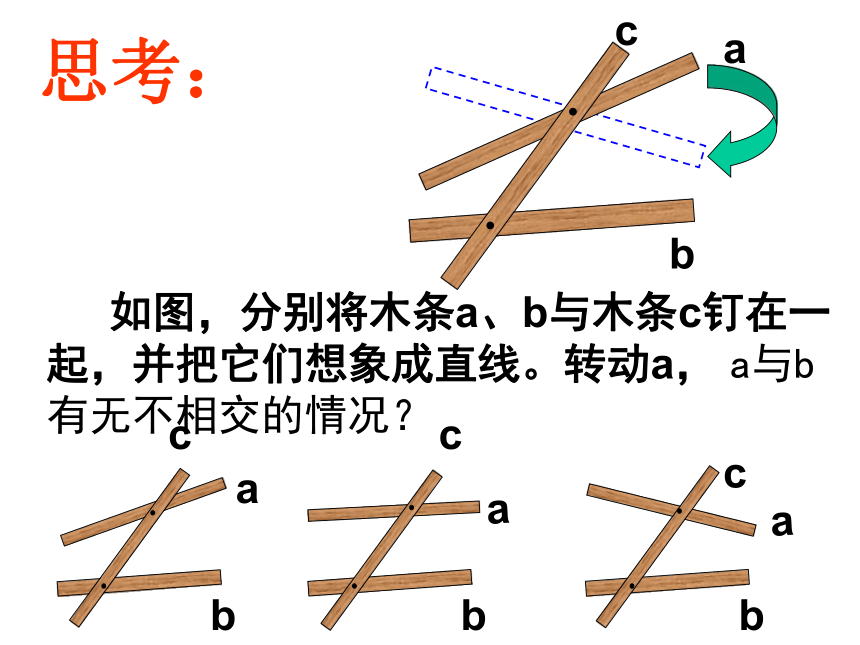
如图,分别将木条a、b与木条c钉在一起,并把它们想象成直线。转动a, a与b 有无不相交的情况?
b
c
a
c
b
a
c
b
a
b
a
c
思考:
平行线的定义:
在同一平面内,不相交的两条直线叫做平行线。
b
a
n
m
C
D
B
A
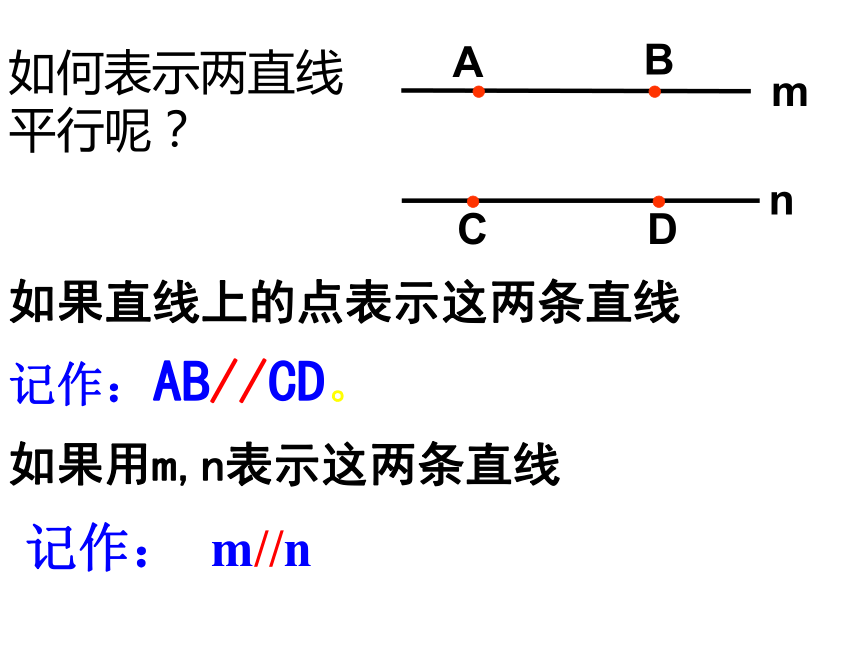
如何表示两直线平行呢?
记作:AB//CD。
如果用m,n表示这两条直线
记作: m//n
如果直线上的点表示这两条直线
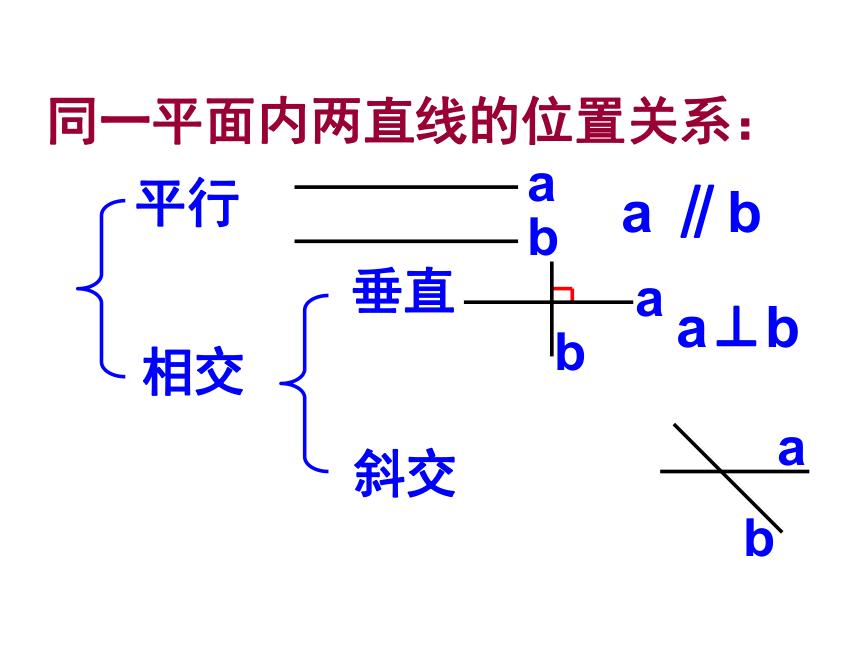
同一平面内两直线的位置关系:
平行
相交
垂直
斜交
a
b
a⊥b
a ∥b
a
b
b
a
一、帖(线)
二、靠(尺)
三、移(点)
四、画(线)
0 1 2 3 4 5
0 1 2 3 4 5 6 7 8 9 10
0 1 2 3 4 5 6 7 8 9 10
0 1 2 3 4 5 6 7 8 9 10
0 1 2 3 4 5
0 1 2 3 4 5
●
过已知直线外一点画它的平行线.
你能用移动三角尺的方法画两条平行线吗?
c
b
a
c
b
a
b
a
在活动木条a的过程中,
有几个位置使得a与b平行;
b
c
a
如图,过点B画直线a的平行线,能画出几条?再过点C画直线a的平行线,它和前面过点B画出的直线平行吗?
C
B
a
讨论
B
1.如图:经过点B能画几条直线与直线a平行
a
经过直线外一点,有且只有一条直线和已知直线平行
b
通过观察和画图,可以体验一个基本事实(平行公理):
2.过点C画一条直线与直线a平行,它与上题中所画的直线b平行吗?
3.通过画图,你发现了什么?
a
B
平行
C
b
平行公理推论:
如果两条直线都和第三条直线平行,那么这两条直线也互相平行。
平行线具有传递性。
b
a
c
∵ b∥a b ∥ c
∴ a ∥c
1.判断正错(正打“√”,错打“×” )
1.两条不相交的直线叫平行线.
2.在同一平面内的两条直线不平行就相交
3.一条直线的平行线有且只有一条
4.过一点,有且只有一条直线与这条直线平行
5.a,b,c是三条直线,如果a∥b且b∥c则a∥c
练习一下:
6.有且只有一个公共点的两直线是相交直线。
2.在同一平面内,直线a与b满足下列条件
1、a与b没有公共点,则a与b的位置关系_____。
2、a与b有且只有一个公共点,则a与b的位置关系___。
3、若AB∥CD且AB∥EF,______∥_____,理由是_______________________;
平行
相交
CD
EF
平行公理推论
3、下列说法中正确的是( )
A、在同一平面内,两条直线的位置
关系有相交、垂直、平行。
B、在同一平面内如果两条线段不相交,
那么这两条线段平行。
C、在同一平面内,不相交的两条射
线是平行线。
D、在同一平面内,不相交的两直线
是平行线。
D
4.下列说法中错误的个数是:( )
①一条直线的平行线只有一条
② 过一点与已知直线平行的直线有且只有一条
③过直线外一点与这条已知直线平行的直线有且
只有一条
A 、0 B 、1 C 、2 D、3
C
① 过两点有且只有一条直线. ② 两条不同的直线有且只有一个公共点.
③ 过一点有且只有一条直线与己知直线垂直。 ④ 过一点有且只有一条直线与己知直线平行。
(A)1 (B) 2 (C)3 (D)4
5. 在同一平面内,下列说法中,正确的有( )个.
√
×
√
×
B
1.平行线的概念。能用符号表示平行线。
2.会用平移三角板或直尺过已知直线外一点画这条直线的平行线。
3.平行线的两条性质。
如图,分别将木条a、b与木条c钉在一起,并把它们想象成直线。转动a, a与b 有无不相交的情况?
b
c
a
c
b
a
c
b
a
b
a
c
思考:
平行线的定义:
在同一平面内,不相交的两条直线叫做平行线。
b
a
n
m
C
D
B
A
如何表示两直线平行呢?
记作:AB//CD。
如果用m,n表示这两条直线
记作: m//n
如果直线上的点表示这两条直线
同一平面内两直线的位置关系:
平行
相交
垂直
斜交
a
b
a⊥b
a ∥b
a
b
b
a
一、帖(线)
二、靠(尺)
三、移(点)
四、画(线)
0 1 2 3 4 5
0 1 2 3 4 5 6 7 8 9 10
0 1 2 3 4 5 6 7 8 9 10
0 1 2 3 4 5 6 7 8 9 10
0 1 2 3 4 5
0 1 2 3 4 5
●
过已知直线外一点画它的平行线.
你能用移动三角尺的方法画两条平行线吗?
c
b
a
c
b
a
b
a
在活动木条a的过程中,
有几个位置使得a与b平行;
b
c
a
如图,过点B画直线a的平行线,能画出几条?再过点C画直线a的平行线,它和前面过点B画出的直线平行吗?
C
B
a
讨论
B
1.如图:经过点B能画几条直线与直线a平行
a
经过直线外一点,有且只有一条直线和已知直线平行
b
通过观察和画图,可以体验一个基本事实(平行公理):
2.过点C画一条直线与直线a平行,它与上题中所画的直线b平行吗?
3.通过画图,你发现了什么?
a
B
平行
C
b
平行公理推论:
如果两条直线都和第三条直线平行,那么这两条直线也互相平行。
平行线具有传递性。
b
a
c
∵ b∥a b ∥ c
∴ a ∥c
1.判断正错(正打“√”,错打“×” )
1.两条不相交的直线叫平行线.
2.在同一平面内的两条直线不平行就相交
3.一条直线的平行线有且只有一条
4.过一点,有且只有一条直线与这条直线平行
5.a,b,c是三条直线,如果a∥b且b∥c则a∥c
练习一下:
6.有且只有一个公共点的两直线是相交直线。
2.在同一平面内,直线a与b满足下列条件
1、a与b没有公共点,则a与b的位置关系_____。
2、a与b有且只有一个公共点,则a与b的位置关系___。
3、若AB∥CD且AB∥EF,______∥_____,理由是_______________________;
平行
相交
CD
EF
平行公理推论
3、下列说法中正确的是( )
A、在同一平面内,两条直线的位置
关系有相交、垂直、平行。
B、在同一平面内如果两条线段不相交,
那么这两条线段平行。
C、在同一平面内,不相交的两条射
线是平行线。
D、在同一平面内,不相交的两直线
是平行线。
D
4.下列说法中错误的个数是:( )
①一条直线的平行线只有一条
② 过一点与已知直线平行的直线有且只有一条
③过直线外一点与这条已知直线平行的直线有且
只有一条
A 、0 B 、1 C 、2 D、3
C
① 过两点有且只有一条直线. ② 两条不同的直线有且只有一个公共点.
③ 过一点有且只有一条直线与己知直线垂直。 ④ 过一点有且只有一条直线与己知直线平行。
(A)1 (B) 2 (C)3 (D)4
5. 在同一平面内,下列说法中,正确的有( )个.
√
×
√
×
B
1.平行线的概念。能用符号表示平行线。
2.会用平移三角板或直尺过已知直线外一点画这条直线的平行线。
3.平行线的两条性质。
