18.2.2 菱形(第1课)知识点导学导练+检测(含答案)
文档属性
| 名称 | 18.2.2 菱形(第1课)知识点导学导练+检测(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 118.2KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-04-19 18:21:59 | ||
图片预览



文档简介
18.2.2 菱形(第1课)
A双基导学导练
知识点1.菱形的性质:四条边都相等,对角线互相垂直平分,且每条对角线平分一组对角.
1.下列关于菱形的叙述正确的是( )
A.对角线互相平分的四边形是菱形
B.对角线互相平分且相等的四边形是菱形
C.对角线互相垂直的四边形是菱形
D.对角线互相垂直平分的四边形是菱形
菱形具有而矩形不一定具有的性质是( )
A.对角线互相平分 B.对角线互相垂直
C.对角线相等 D.四个角都相等
3.菱形具有而平行四边形不一定具有的性质是( )
A.对边平行 B.对角相等 C.对角线互相平分D.对角线互相垂直
4.菱形ABCD中,∠ABD=20°,则∠ABC的度数为 .∠BCD的度数为 .
5.若菱形的边长为3cm,其中一内角为60°,则它的较短的对角线长为 .
6.菱形边长为7cm,一条对角线为7cm,那么菱形的最大的内角为 .
7.如图,菱形ABCD中,E、F分别是边BC、CD上的点,△AEF是正三角形,若AB=AE,则∠C= .
8.四边形ABCD中,E,F,G,H分别是边AB,BC,CD,DA的中点,请你添加一个条件,使四边形EFGH为菱形,应添加的条件是 .
知识点2.菱形的面积等于两条对角线乘积的一半
9.菱形ABCD中,∠D:∠A=5:1,周长是8cm,则菱形的高是 ,面积是 .
菱形的两条对角线长分别为9cm和4cm,则此菱形的面积是 .
11.如图,菱形的周长为40cm,AC与BD交于O,且BD:AC=4:3,则AC= .BD?=
菱形ABCD的面积为 .
B真题检测反馈
12.如图,菱形ABCD中,F是AB上一点,DF交AC于E,求证:∠AFD=∠CBE
13.如图,菱形ABCD中,E、F别在AB、AD上,且AE=AF,求证:CE=CF
如图,已知菱形ABCD,AB=AE,且∠EAD=2∠EAB.求证:BE=AF
15.如图,把△FEP放置在菱形ABCD中,使得顶点E,F,P分别在线段AB,AD,AC上,已知EP=FP=6,EF=false ,∠BAD=60°,且AB>false
(1)求∠EPF的度数;
(2)若AP=10,求AE+AF的值
C 创新拓展提升
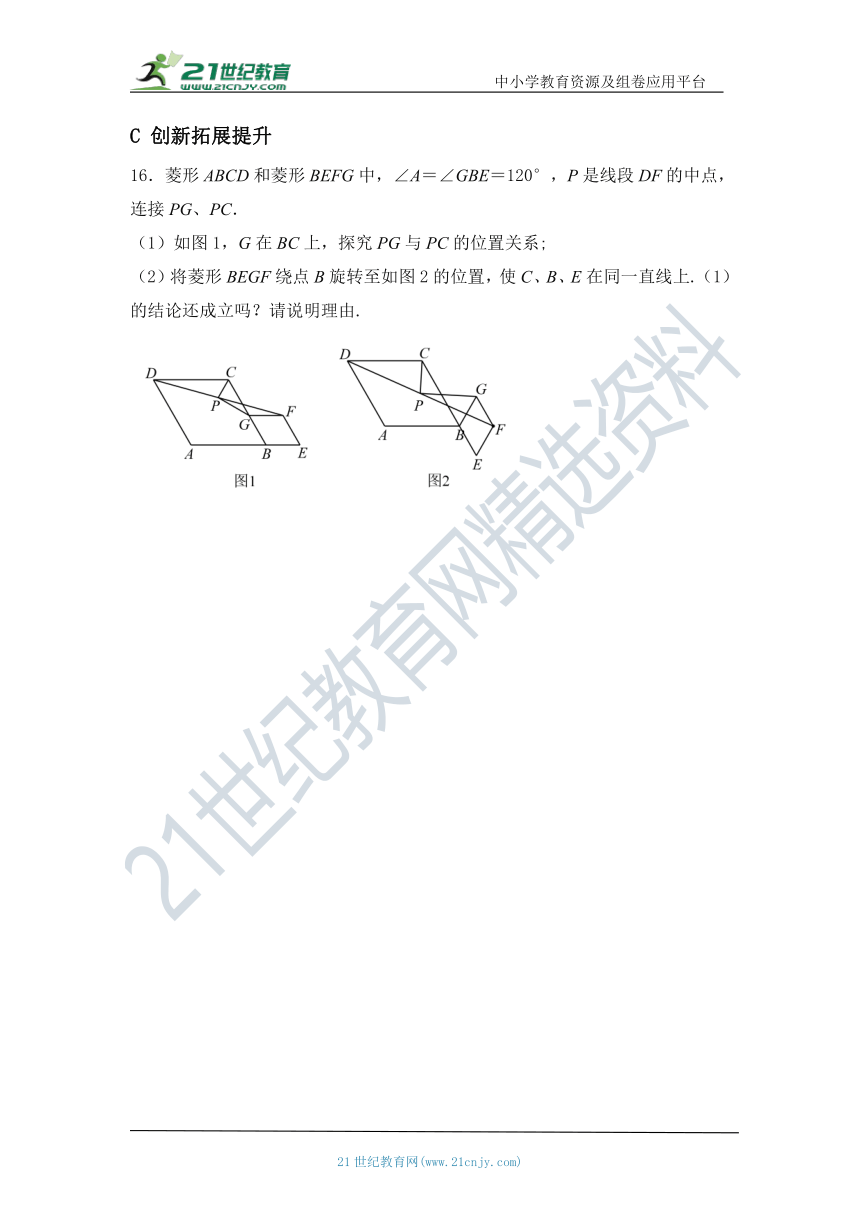
16.菱形ABCD和菱形BEFG中,∠A=∠GBE=120°,P是线段DF的中点,连接PG、PC.
(1)如图1,G在BC上,探究PG与PC的位置关系;
(2)将菱形BEGF绕点B旋转至如图2的位置,使C、B、E在同一直线上.(1)的结论还成立吗?请说明理由.
18.2.2 菱形(第1课)
A双基导学导练
知识点1.菱形的性质:四条边都相等,对角线互相垂直平分,且每条对角线平分一组对角.
1.下列关于菱形的叙述正确的是( )
A.对角线互相平分的四边形是菱形
B.对角线互相平分且相等的四边形是菱形
C.对角线互相垂直的四边形是菱形
D.对角线互相垂直平分的四边形是菱形
答案: D
2.菱形具有而矩形不一定具有的性质是( )
A.对角线互相平分 B.对角线互相垂直
C.对角线相等 D.四个角都相等
答案: B
菱形具有而平行四边形不一定具有的性质是( )
A.对边平行 B.对角相等 C.对角线互相平分D.对角线互相垂直
答案:D
菱形ABCD中,∠ABD=20°,则∠ABC的度数为 .∠BCD的度数为 .
答案:40°, 140°
若菱形的边长为3cm,其中一内角为60°,则它的较短的对角线长为 .
答案:3cm
菱形边长为7cm,一条对角线为7cm,那么菱形的最大的内角为 .
答案:120°
7.如图,菱形ABCD中,E、F分别是边BC、CD上的点,△AEF是正三角形,若AB=AE,则∠C= .
答案:100°
8.四边形ABCD中,E,F,G,H分别是边AB,BC,CD,DA的中点,请你添加一个条件,使四边形EFGH为菱形,应添加的条件是 .
答案:AC=BD
知识点2.菱形的面积等于两条对角线乘积的一半
9.菱形ABCD中,∠D:∠A=5:1,周长是8cm,则菱形的高是 ,面积是 .
答案:1cm,2cm2
10.菱形的两条对角线长分别为9cm和4cm,则此菱形的面积是 .
答案:18cm2
11.如图,菱形的周长为40cm,AC与BD交于O,且BD:AC=4:3,则AC= .BD?=
菱形ABCD的面积为 .
答案:12cm ,16cm ,96cm2
B真题检测反馈
12.如图,菱形ABCD中,F是AB上一点,DF交AC于E,求证:∠AFD=∠CBE
答案:
证明:由AB∥CD可得∠AFD=∠CDF 又由△CBE≌△CDE得∠CBE=∠CDE
从而∠AFD=∠CBE
13.如图,菱形ABCD中,E、F别在AB、AD上,且AE=AF,求证:CE=CF
答案:
证法一:连AC,△CAE≌△CAF ∴CE=CF
证法二:证△CBE≌△CDF
14.如图,已知菱形ABCD,AB=AE,且∠EAD=2∠EAB.求证:BE=AF
答案:
证明:∵?AD∥BC ∴∠AEB=∠DAE=2∠EAB∴∠BAE=∠ABF=∠FBE=36°,
∠AEB=72°∴BE=BF=AF
15.如图,把△FEP放置在菱形ABCD中,使得顶点E,F,P分别在线段AB,AD,AC上,已知EP=FP=6,EF=false ,∠BAD=60°,且AB>false
(1)求∠EPF的度数;
(2)若AP=10,求AE+AF的值
答案:
解:(1)过点P作PG⊥EF于G,∵PE=PF=6,EF=false
∴FG=EG=false , ?∠PPG=∠EPG= false∠EPF
在Rt△FPG中,FG=3,false, ∴∠PFG=30°, ∴∠EPF=2∠FPG=120°
(2)作PM⊥AB于M.PN⊥AD于N
∵AC为菱形ABCD的对角线 ,∴∠DAC=∠BAC,AM=AN,PM=PN
在Rt△PME和Rt△PNF中,PM=PN,PE=PF ∴△PME≌△PNF∴MF=ME
又∵AP=10,∠PAM=false ∠DAB=30°∴AM=AN=false
∴AE+AF=(AM+ME)+(AN-NF)=AM+AN= false
C 创新拓展提升
16.菱形ABCD和菱形BEFG中,∠A=∠GBE=120°,P是线段DF的中点,连接PG、PC.
(1)如图1,G在BC上,探究PG与PC的位置关系;
(2)将菱形BEGF绕点B旋转至如图2的位置,使C、B、E在同一直线上.(1)的结论还成立吗?请说明理由.
答案:
解:(1)延长GP交CD于点M,可证△DPM≌△FPG(ASA)
∴DM=GF ∵CD=BC? ∴MC=DC-DM=?BC-BG=CG
又∵AP=PG∴CP⊥PG
(2)延长GP交AD于点M,连接CM、CC,可证△DMP≌△FGP(ASA)
∴PM=PG,?DM=GF 又∵CD=BC且GF=GB=DM ,
∴△CDM≌△CBG(SAS)∴CM=CG ∴PC⊥PG
A双基导学导练
知识点1.菱形的性质:四条边都相等,对角线互相垂直平分,且每条对角线平分一组对角.
1.下列关于菱形的叙述正确的是( )
A.对角线互相平分的四边形是菱形
B.对角线互相平分且相等的四边形是菱形
C.对角线互相垂直的四边形是菱形
D.对角线互相垂直平分的四边形是菱形
菱形具有而矩形不一定具有的性质是( )
A.对角线互相平分 B.对角线互相垂直
C.对角线相等 D.四个角都相等
3.菱形具有而平行四边形不一定具有的性质是( )
A.对边平行 B.对角相等 C.对角线互相平分D.对角线互相垂直
4.菱形ABCD中,∠ABD=20°,则∠ABC的度数为 .∠BCD的度数为 .
5.若菱形的边长为3cm,其中一内角为60°,则它的较短的对角线长为 .
6.菱形边长为7cm,一条对角线为7cm,那么菱形的最大的内角为 .
7.如图,菱形ABCD中,E、F分别是边BC、CD上的点,△AEF是正三角形,若AB=AE,则∠C= .
8.四边形ABCD中,E,F,G,H分别是边AB,BC,CD,DA的中点,请你添加一个条件,使四边形EFGH为菱形,应添加的条件是 .
知识点2.菱形的面积等于两条对角线乘积的一半
9.菱形ABCD中,∠D:∠A=5:1,周长是8cm,则菱形的高是 ,面积是 .
菱形的两条对角线长分别为9cm和4cm,则此菱形的面积是 .
11.如图,菱形的周长为40cm,AC与BD交于O,且BD:AC=4:3,则AC= .BD?=
菱形ABCD的面积为 .
B真题检测反馈
12.如图,菱形ABCD中,F是AB上一点,DF交AC于E,求证:∠AFD=∠CBE
13.如图,菱形ABCD中,E、F别在AB、AD上,且AE=AF,求证:CE=CF
如图,已知菱形ABCD,AB=AE,且∠EAD=2∠EAB.求证:BE=AF
15.如图,把△FEP放置在菱形ABCD中,使得顶点E,F,P分别在线段AB,AD,AC上,已知EP=FP=6,EF=false ,∠BAD=60°,且AB>false
(1)求∠EPF的度数;
(2)若AP=10,求AE+AF的值
C 创新拓展提升
16.菱形ABCD和菱形BEFG中,∠A=∠GBE=120°,P是线段DF的中点,连接PG、PC.
(1)如图1,G在BC上,探究PG与PC的位置关系;
(2)将菱形BEGF绕点B旋转至如图2的位置,使C、B、E在同一直线上.(1)的结论还成立吗?请说明理由.
18.2.2 菱形(第1课)
A双基导学导练
知识点1.菱形的性质:四条边都相等,对角线互相垂直平分,且每条对角线平分一组对角.
1.下列关于菱形的叙述正确的是( )
A.对角线互相平分的四边形是菱形
B.对角线互相平分且相等的四边形是菱形
C.对角线互相垂直的四边形是菱形
D.对角线互相垂直平分的四边形是菱形
答案: D
2.菱形具有而矩形不一定具有的性质是( )
A.对角线互相平分 B.对角线互相垂直
C.对角线相等 D.四个角都相等
答案: B
菱形具有而平行四边形不一定具有的性质是( )
A.对边平行 B.对角相等 C.对角线互相平分D.对角线互相垂直
答案:D
菱形ABCD中,∠ABD=20°,则∠ABC的度数为 .∠BCD的度数为 .
答案:40°, 140°
若菱形的边长为3cm,其中一内角为60°,则它的较短的对角线长为 .
答案:3cm
菱形边长为7cm,一条对角线为7cm,那么菱形的最大的内角为 .
答案:120°
7.如图,菱形ABCD中,E、F分别是边BC、CD上的点,△AEF是正三角形,若AB=AE,则∠C= .
答案:100°
8.四边形ABCD中,E,F,G,H分别是边AB,BC,CD,DA的中点,请你添加一个条件,使四边形EFGH为菱形,应添加的条件是 .
答案:AC=BD
知识点2.菱形的面积等于两条对角线乘积的一半
9.菱形ABCD中,∠D:∠A=5:1,周长是8cm,则菱形的高是 ,面积是 .
答案:1cm,2cm2
10.菱形的两条对角线长分别为9cm和4cm,则此菱形的面积是 .
答案:18cm2
11.如图,菱形的周长为40cm,AC与BD交于O,且BD:AC=4:3,则AC= .BD?=
菱形ABCD的面积为 .
答案:12cm ,16cm ,96cm2
B真题检测反馈
12.如图,菱形ABCD中,F是AB上一点,DF交AC于E,求证:∠AFD=∠CBE
答案:
证明:由AB∥CD可得∠AFD=∠CDF 又由△CBE≌△CDE得∠CBE=∠CDE
从而∠AFD=∠CBE
13.如图,菱形ABCD中,E、F别在AB、AD上,且AE=AF,求证:CE=CF
答案:
证法一:连AC,△CAE≌△CAF ∴CE=CF
证法二:证△CBE≌△CDF
14.如图,已知菱形ABCD,AB=AE,且∠EAD=2∠EAB.求证:BE=AF
答案:
证明:∵?AD∥BC ∴∠AEB=∠DAE=2∠EAB∴∠BAE=∠ABF=∠FBE=36°,
∠AEB=72°∴BE=BF=AF
15.如图,把△FEP放置在菱形ABCD中,使得顶点E,F,P分别在线段AB,AD,AC上,已知EP=FP=6,EF=false ,∠BAD=60°,且AB>false
(1)求∠EPF的度数;
(2)若AP=10,求AE+AF的值
答案:
解:(1)过点P作PG⊥EF于G,∵PE=PF=6,EF=false
∴FG=EG=false , ?∠PPG=∠EPG= false∠EPF
在Rt△FPG中,FG=3,false, ∴∠PFG=30°, ∴∠EPF=2∠FPG=120°
(2)作PM⊥AB于M.PN⊥AD于N
∵AC为菱形ABCD的对角线 ,∴∠DAC=∠BAC,AM=AN,PM=PN
在Rt△PME和Rt△PNF中,PM=PN,PE=PF ∴△PME≌△PNF∴MF=ME
又∵AP=10,∠PAM=false ∠DAB=30°∴AM=AN=false
∴AE+AF=(AM+ME)+(AN-NF)=AM+AN= false
C 创新拓展提升
16.菱形ABCD和菱形BEFG中,∠A=∠GBE=120°,P是线段DF的中点,连接PG、PC.
(1)如图1,G在BC上,探究PG与PC的位置关系;
(2)将菱形BEGF绕点B旋转至如图2的位置,使C、B、E在同一直线上.(1)的结论还成立吗?请说明理由.
答案:
解:(1)延长GP交CD于点M,可证△DPM≌△FPG(ASA)
∴DM=GF ∵CD=BC? ∴MC=DC-DM=?BC-BG=CG
又∵AP=PG∴CP⊥PG
(2)延长GP交AD于点M,连接CM、CC,可证△DMP≌△FGP(ASA)
∴PM=PG,?DM=GF 又∵CD=BC且GF=GB=DM ,
∴△CDM≌△CBG(SAS)∴CM=CG ∴PC⊥PG
