18.2.3 正方形(第1课时)知识点导学导练+检测(含答案)
文档属性
| 名称 | 18.2.3 正方形(第1课时)知识点导学导练+检测(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 131.4KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-04-19 18:21:26 | ||
图片预览

文档简介
18.2.3正方形(第1课时)
A.双基导学导练
知识点:正方形的性质:四条边都相等、四个角都是直角、对角线相等且相互垂直平分
1.正方形具有而矩形不一定具有的性质( )
A. 四个角都是直角 B. 对角线互相平分
C. 对角线相互垂直 D.对角线相等
2. 正方形具有而菱形不一定具有的性质( )
A.四条边都相等 B.对角线互相垂直平分
C.对角线相等 D.每一条对角线平分一组对角
3.正方形是ABCD中,连接两条对角线,则共可得到( )个等腰直角三角形.
A. 10个 B.8个 C. 6个 D.5个
4.正方形既是特殊的 ,又是特殊的 ,它的四个角都是 ,四条边都 ,对角线 ,并且每条对角线 .
5.下列结论,①正方形具有平行四边形的一切性质:②正方形具有矩形的一切性质,③正方形具有菱形的一切性质,其中正确的结论有 个
6.矩形有 条对称轴,菱形有 条对称轴,正方形有 条对称轴。
7.已知正方形ABCD,等边△ABE,则∠ADE的度数为 .
8.如图,正方形ABCD的周长为16cm,顺次连接正方形ABCD各边的中点,得到四边形 EFCH,则它的形状是 ,它的周长等于 cm.
51308098425
B真题检测反馈
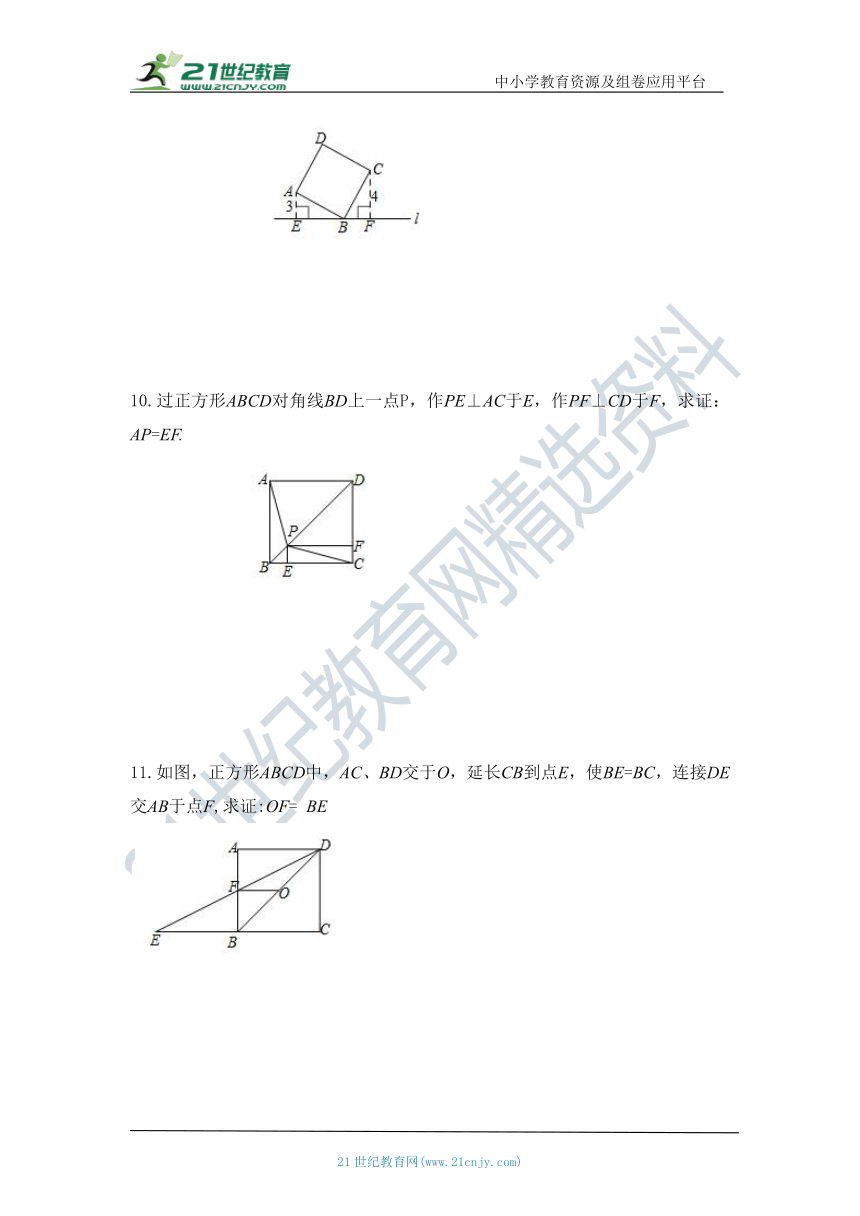
9.如图,直线l过正方形ABCD的顶点B,点A、C到直线l的距离分别是3和5.则
正方形的边长为 .
117157534925
10.过正方形ABCD对角线BD上一点P,作PE⊥AC于E,作PF⊥CD于F,求证:AP=EF.
100012553975
11.如图,正方形ABCD中,AC、BD交于O,延长CB到点E,使BE=BC,连接DE交AB于点F,求证:OF= BE
476256350
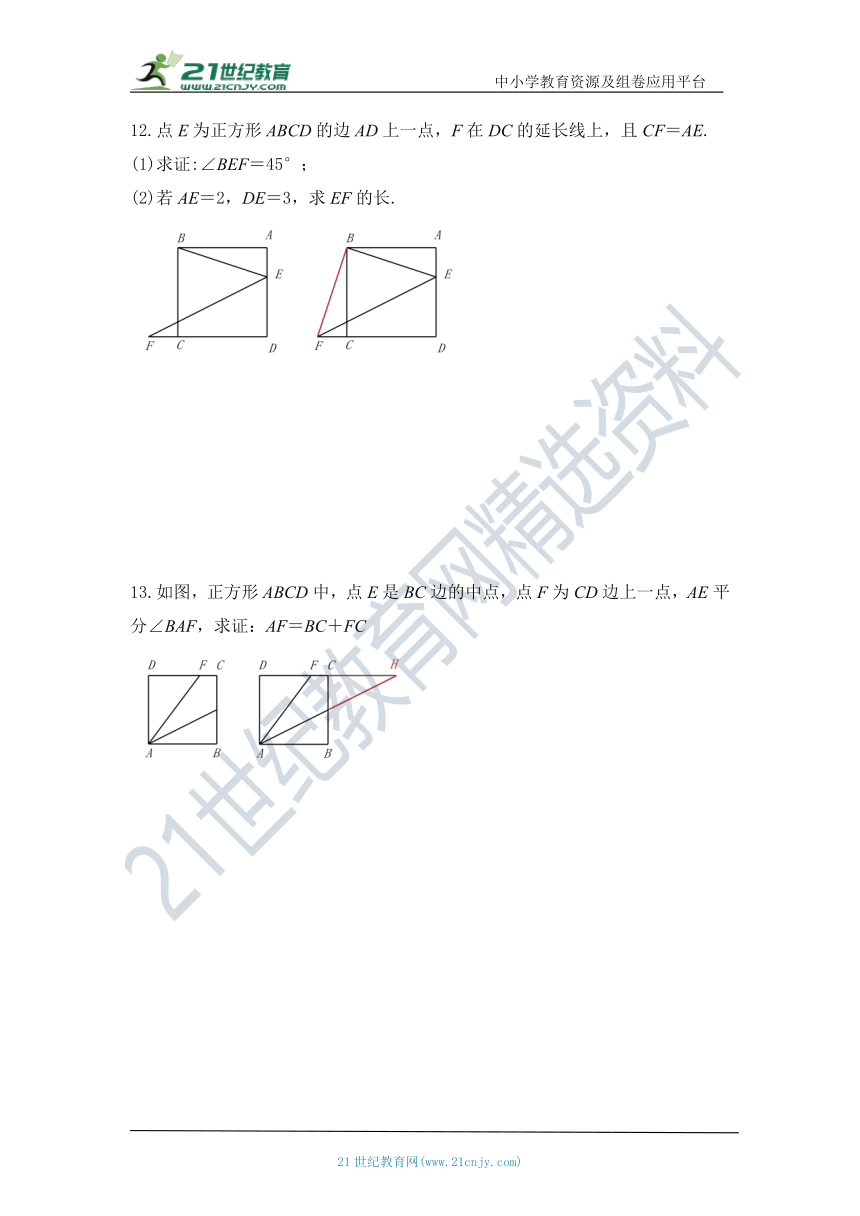
12.点E为正方形ABCD的边AD上一点,F在DC的延长线上,且CF=AE.
(1)求证:∠BEF=45°;
(2)若AE=2,DE=3,求EF的长.
13.如图,正方形ABCD中,点E是BC边的中点,点F为CD边上一点,AE平分∠BAF,求证:AF=BC+FC
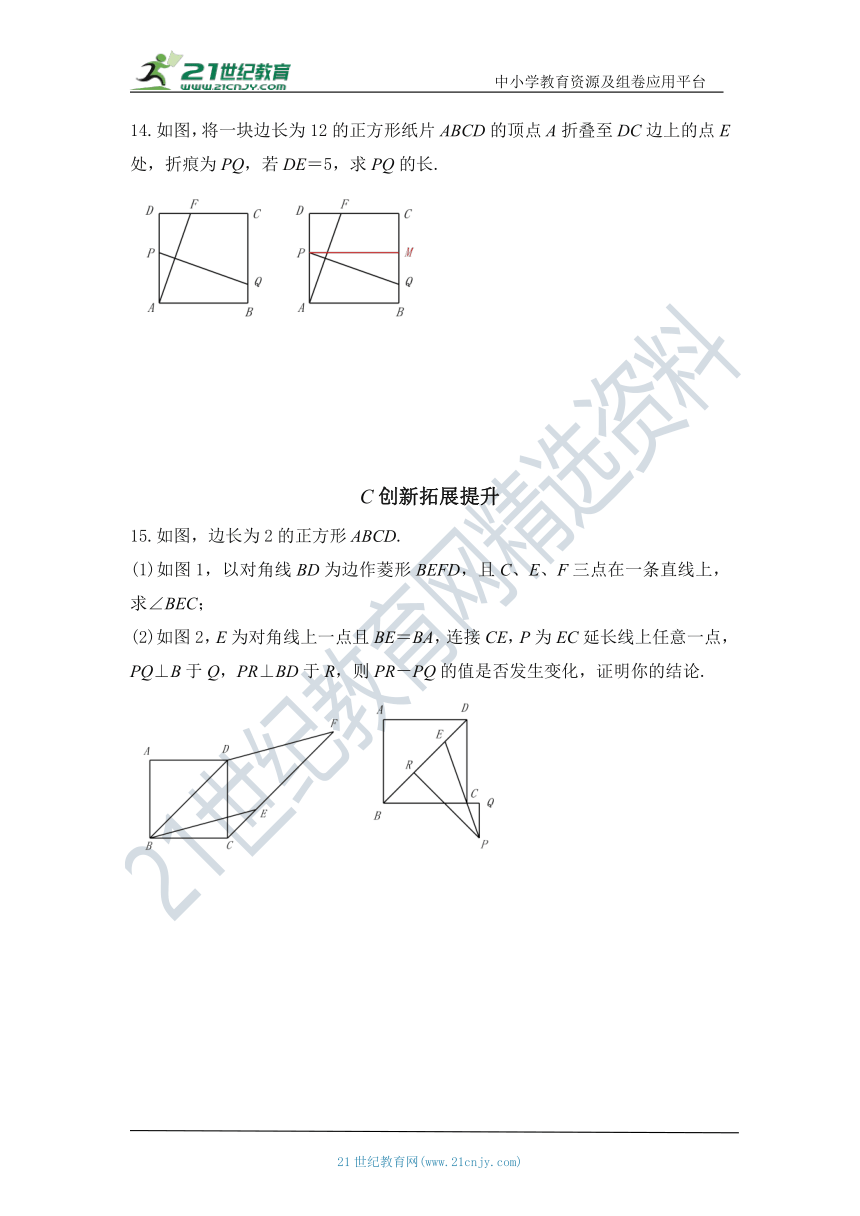
14.如图,将一块边长为12的正方形纸片ABCD的顶点A折叠至DC边上的点E处,折痕为PQ,若DE=5,求PQ的长.
C创新拓展提升
15.如图,边长为2的正方形ABCD.
(1)如图1,以对角线BD为边作菱形BEFD,且C、E、F三点在一条直线上,求∠BEC;
(2)如图2,E为对角线上一点且BE=BA,连接CE,P为EC延长线上任意一点,PQ⊥B于Q,PR⊥BD于R,则PR-PQ的值是否发生变化,证明你的结论.
18.2.3正方形(第1课时)
A.双基导学导练
知识点:正方形的性质:四条边都相等、四个角都是直角、对角线相等且相互垂直平分
1.正方形具有而矩形不一定具有的性质( )
A. 四个角都是直角 B. 对角线互相平分
C. 对角线相互垂直 D.对角线相等
答案: C
2. 正方形具有而菱形不一定具有的性质( )
A.四条边都相等 B.对角线互相垂直平分
C.对角线相等 D.每一条对角线平分一组对角
答案:C
3.正方形是ABCD中,连接两条对角线,则共可得到( )个等腰直角三角形.
A. 10个 B.8个 C. 6个 D.5个
答案: B
4.正方形既是特殊的 ,又是特殊的 ,它的四个角都是 ,四条边都 ,对角线 ,并且每条对角线 .
答案:矩形 , 菱形 , 90°,相等 ,互相垂直平分且相等,平分一组对角
5.下列结论,①正方形具有平行四边形的一切性质:②正方形具有矩形的一切性质,③正方形具有菱形的一切性质,其中正确的结论有 个
答案:3
6.矩形有 条对称轴,菱形有 条对称轴,正方形有 条对称轴。
答案:2, 2,4
7.已知正方形ABCD,等边△ABE,则∠ADE的度数为 .
答案:75°或15°
8.如图,正方形ABCD的周长为16cm,顺次连接正方形ABCD各边的中点,得到四边形 EFCH,则它的形状是 ,它的周长等于 cm.
答案: 正方形, false
51308098425
B真题检测反馈
9.如图,直线l过正方形ABCD的顶点B,点A、C到直线l的距离分别是3和5.则
正方形的边长为 .
1187450216535答案:false
99250552895510.过正方形ABCD对角线BD上一点P,作PE⊥AC于E,作PF⊥CD于F,求证:AP=EF.
答案:
证明:连接PC,由对称性可知AP=PC AC=EF∴AP=EF
如图,正方形ABCD中,AC、BD交于O,延长CB到点E,使BE=BC,连接DE交AB于点F,求证:OF= BE
206375127000
答案:
证明,可证:△ADF ≌ △BEF, FD=FE 又∵OD=OB, ∴ OF=false BE
12.点E为正方形ABCD的边AD上一点,F在DC的延长线上,且CF=AE.
(1)求证:∠BEF=45°;
(2)若AE=2,DE=3,求EF的长.
答案:(1)连接BF,证△ABE≌△CBF,∴△BEF的为等腰直角三角形,∴∠BEF=45°
(2)由(1)得EF=falseBE=false×false=false
13.如图,正方形ABCD中,点E是BC边的中点,点F为CD边上一点,AE平分∠BAF,
求证:AF=BC+FC
证明:延长AE交DC的延长线于H,易证△ABE≌△HCE得AB=HC=BC
由AB∥CD得∠BAE=∠H
∵∠FAE=∠BAE
∴∠FAE=∠H
∴AF= HF= HC+ FC= BC+FC
14.如图,将一块边长为12的正方形纸片ABCD的顶点A折叠至DC边上的点E处,折痕为PQ,若DE=5,求PQ的长.
解:过P作PM⊥BC于点M,易证△PMQ≌△ADE
∴PQ=AE=false=13
C创新拓展提升
15.如图,边长为2的正方形ABCD.
(1)如图1,以对角线BD为边作菱形BEFD,且C、E、F三点在一条直线上,求∠BEC;
(2)如图2,E为对角线上一点且BE=BA,连接CE,P为EC延长线上任意一点,PQ⊥B于Q,PR⊥BD于R,则PR-PQ的值是否发生变化,证明你的结论.
解:(1)连接AC交BD于O,作EQ⊥BD
∴OC=EQ=falseAC=falseBD=falseBE ∴∠DBE=30°∴∠BEC=30°
(2)连接AC交BD于O,作CM⊥PR
易得四边形ORMC为矩形,△PQC≌△PMC,∴PR-PQ=PR-PM=RM=OC=false
A.双基导学导练
知识点:正方形的性质:四条边都相等、四个角都是直角、对角线相等且相互垂直平分
1.正方形具有而矩形不一定具有的性质( )
A. 四个角都是直角 B. 对角线互相平分
C. 对角线相互垂直 D.对角线相等
2. 正方形具有而菱形不一定具有的性质( )
A.四条边都相等 B.对角线互相垂直平分
C.对角线相等 D.每一条对角线平分一组对角
3.正方形是ABCD中,连接两条对角线,则共可得到( )个等腰直角三角形.
A. 10个 B.8个 C. 6个 D.5个
4.正方形既是特殊的 ,又是特殊的 ,它的四个角都是 ,四条边都 ,对角线 ,并且每条对角线 .
5.下列结论,①正方形具有平行四边形的一切性质:②正方形具有矩形的一切性质,③正方形具有菱形的一切性质,其中正确的结论有 个
6.矩形有 条对称轴,菱形有 条对称轴,正方形有 条对称轴。
7.已知正方形ABCD,等边△ABE,则∠ADE的度数为 .
8.如图,正方形ABCD的周长为16cm,顺次连接正方形ABCD各边的中点,得到四边形 EFCH,则它的形状是 ,它的周长等于 cm.
51308098425
B真题检测反馈
9.如图,直线l过正方形ABCD的顶点B,点A、C到直线l的距离分别是3和5.则
正方形的边长为 .
117157534925
10.过正方形ABCD对角线BD上一点P,作PE⊥AC于E,作PF⊥CD于F,求证:AP=EF.
100012553975
11.如图,正方形ABCD中,AC、BD交于O,延长CB到点E,使BE=BC,连接DE交AB于点F,求证:OF= BE
476256350
12.点E为正方形ABCD的边AD上一点,F在DC的延长线上,且CF=AE.
(1)求证:∠BEF=45°;
(2)若AE=2,DE=3,求EF的长.
13.如图,正方形ABCD中,点E是BC边的中点,点F为CD边上一点,AE平分∠BAF,求证:AF=BC+FC
14.如图,将一块边长为12的正方形纸片ABCD的顶点A折叠至DC边上的点E处,折痕为PQ,若DE=5,求PQ的长.
C创新拓展提升
15.如图,边长为2的正方形ABCD.
(1)如图1,以对角线BD为边作菱形BEFD,且C、E、F三点在一条直线上,求∠BEC;
(2)如图2,E为对角线上一点且BE=BA,连接CE,P为EC延长线上任意一点,PQ⊥B于Q,PR⊥BD于R,则PR-PQ的值是否发生变化,证明你的结论.
18.2.3正方形(第1课时)
A.双基导学导练
知识点:正方形的性质:四条边都相等、四个角都是直角、对角线相等且相互垂直平分
1.正方形具有而矩形不一定具有的性质( )
A. 四个角都是直角 B. 对角线互相平分
C. 对角线相互垂直 D.对角线相等
答案: C
2. 正方形具有而菱形不一定具有的性质( )
A.四条边都相等 B.对角线互相垂直平分
C.对角线相等 D.每一条对角线平分一组对角
答案:C
3.正方形是ABCD中,连接两条对角线,则共可得到( )个等腰直角三角形.
A. 10个 B.8个 C. 6个 D.5个
答案: B
4.正方形既是特殊的 ,又是特殊的 ,它的四个角都是 ,四条边都 ,对角线 ,并且每条对角线 .
答案:矩形 , 菱形 , 90°,相等 ,互相垂直平分且相等,平分一组对角
5.下列结论,①正方形具有平行四边形的一切性质:②正方形具有矩形的一切性质,③正方形具有菱形的一切性质,其中正确的结论有 个
答案:3
6.矩形有 条对称轴,菱形有 条对称轴,正方形有 条对称轴。
答案:2, 2,4
7.已知正方形ABCD,等边△ABE,则∠ADE的度数为 .
答案:75°或15°
8.如图,正方形ABCD的周长为16cm,顺次连接正方形ABCD各边的中点,得到四边形 EFCH,则它的形状是 ,它的周长等于 cm.
答案: 正方形, false
51308098425
B真题检测反馈
9.如图,直线l过正方形ABCD的顶点B,点A、C到直线l的距离分别是3和5.则
正方形的边长为 .
1187450216535答案:false
99250552895510.过正方形ABCD对角线BD上一点P,作PE⊥AC于E,作PF⊥CD于F,求证:AP=EF.
答案:
证明:连接PC,由对称性可知AP=PC AC=EF∴AP=EF
如图,正方形ABCD中,AC、BD交于O,延长CB到点E,使BE=BC,连接DE交AB于点F,求证:OF= BE
206375127000
答案:
证明,可证:△ADF ≌ △BEF, FD=FE 又∵OD=OB, ∴ OF=false BE
12.点E为正方形ABCD的边AD上一点,F在DC的延长线上,且CF=AE.
(1)求证:∠BEF=45°;
(2)若AE=2,DE=3,求EF的长.
答案:(1)连接BF,证△ABE≌△CBF,∴△BEF的为等腰直角三角形,∴∠BEF=45°
(2)由(1)得EF=falseBE=false×false=false
13.如图,正方形ABCD中,点E是BC边的中点,点F为CD边上一点,AE平分∠BAF,
求证:AF=BC+FC
证明:延长AE交DC的延长线于H,易证△ABE≌△HCE得AB=HC=BC
由AB∥CD得∠BAE=∠H
∵∠FAE=∠BAE
∴∠FAE=∠H
∴AF= HF= HC+ FC= BC+FC
14.如图,将一块边长为12的正方形纸片ABCD的顶点A折叠至DC边上的点E处,折痕为PQ,若DE=5,求PQ的长.
解:过P作PM⊥BC于点M,易证△PMQ≌△ADE
∴PQ=AE=false=13
C创新拓展提升
15.如图,边长为2的正方形ABCD.
(1)如图1,以对角线BD为边作菱形BEFD,且C、E、F三点在一条直线上,求∠BEC;
(2)如图2,E为对角线上一点且BE=BA,连接CE,P为EC延长线上任意一点,PQ⊥B于Q,PR⊥BD于R,则PR-PQ的值是否发生变化,证明你的结论.
解:(1)连接AC交BD于O,作EQ⊥BD
∴OC=EQ=falseAC=falseBD=falseBE ∴∠DBE=30°∴∠BEC=30°
(2)连接AC交BD于O,作CM⊥PR
易得四边形ORMC为矩形,△PQC≌△PMC,∴PR-PQ=PR-PM=RM=OC=false
