18.2.1 矩形(第1课时)知识点导学导练+检测(含答案)
文档属性
| 名称 | 18.2.1 矩形(第1课时)知识点导学导练+检测(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 113.5KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-04-19 18:17:33 | ||
图片预览

文档简介
18.2.1矩形(第1课时)
A双基导学导练
知识点1 矩形是一个角是直角的平行四边形,具有平行四边形的性质,还具有四个角是直角,对角线相等的性质
如图,矩形ABCD中,ABA.2个 B.4个 C.6个 D.8个
2.矩形的周长为22cm,一条边长为7cm,则另一条边长为__________,面积为__________
3.矩形ABCD中,对角线AC、BD相交于点O,AB=8,BC=6,则对角线AC的长为_________,AO的长为____________
4.如图,在矩形ABCD中,对角线AC、BD相交于点O,∠AOB=60°,AB=4,则BC=_______
5.矩形的对角线相交所成的锐角是60°,短边的长为3cm,则对角线的长为______,长边的长为________________
6.如图,在△ABC中,∠ABC=90°,D是AC的中点,若∠A=25°,则∠BDC=_______,∠CBD=__________
知识点2 直角三角形斜边上的中线等于斜边的一半
7.直角三角形中,两直角边分别是6和8,则斜边上的中线是______________
8.如图,矩形ABCD中,若AD=1,AB=false,则DO=_________,∠DOA的度数是________
9.如图,矩形ABCD中,AB=3cm,AE平分∠BAD交BC于E,则AE的长是__________cm
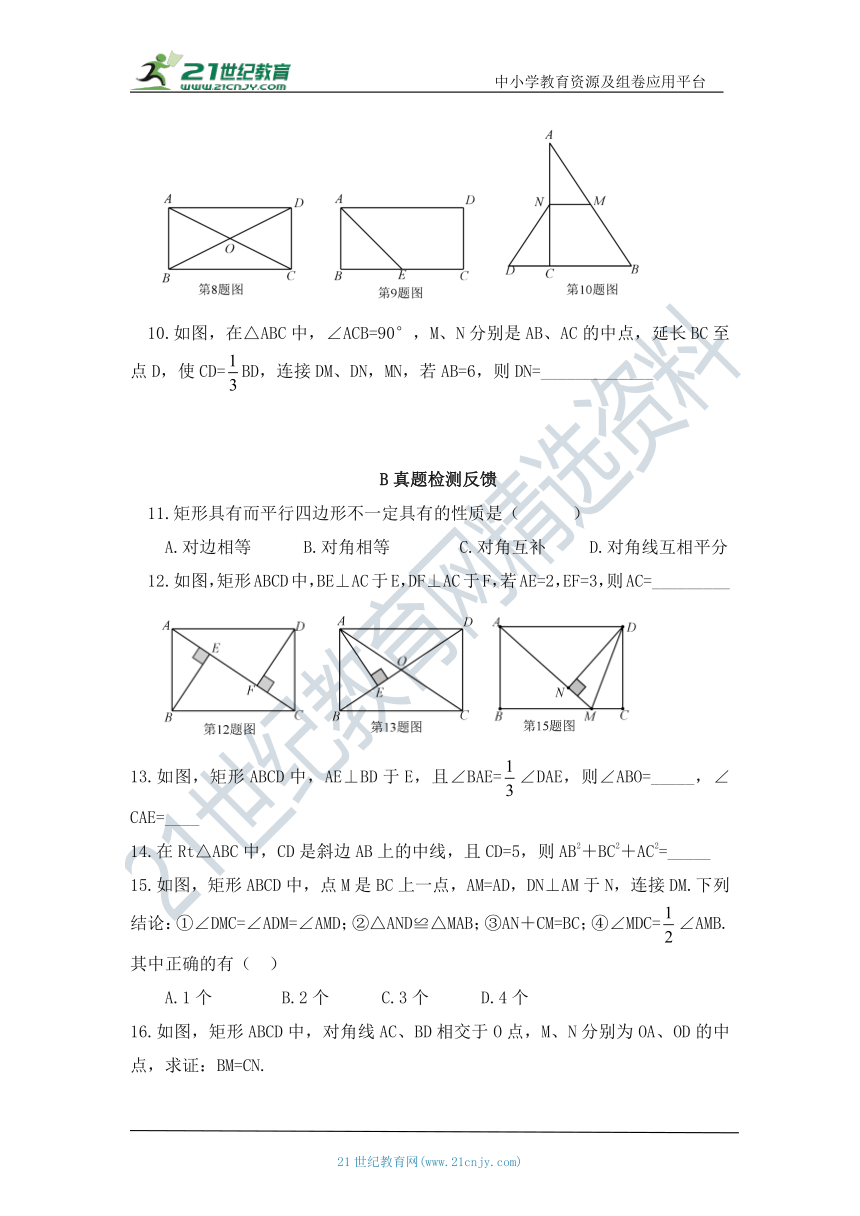
10.如图,在△ABC中,∠ACB=90°,M、N分别是AB、AC的中点,延长BC至点D,使CD=falseBD,连接DM、DN,MN,若AB=6,则DN=_____________
B真题检测反馈
11.矩形具有而平行四边形不一定具有的性质是( )
A.对边相等 B.对角相等 C.对角互补 D.对角线互相平分
12.如图,矩形ABCD中,BE⊥AC于E,DF⊥AC于F,若AE=2,EF=3,则AC=_________
13.如图,矩形ABCD中,AE⊥BD于E,且∠BAE=false∠DAE,则∠ABO=_____,∠CAE=____
14.在Rt△ABC中,CD是斜边AB上的中线,且CD=5,则AB2+BC2+AC2=_____
15.如图,矩形ABCD中,点M是BC上一点,AM=AD,DN⊥AM于N,连接DM.下列结论:①∠DMC=∠ADM=∠AMD;②△AND≌△MAB;③AN+CM=BC;④∠MDC=false∠AMB.其中正确的有( )
A.1个 B.2个 C.3个 D.4个
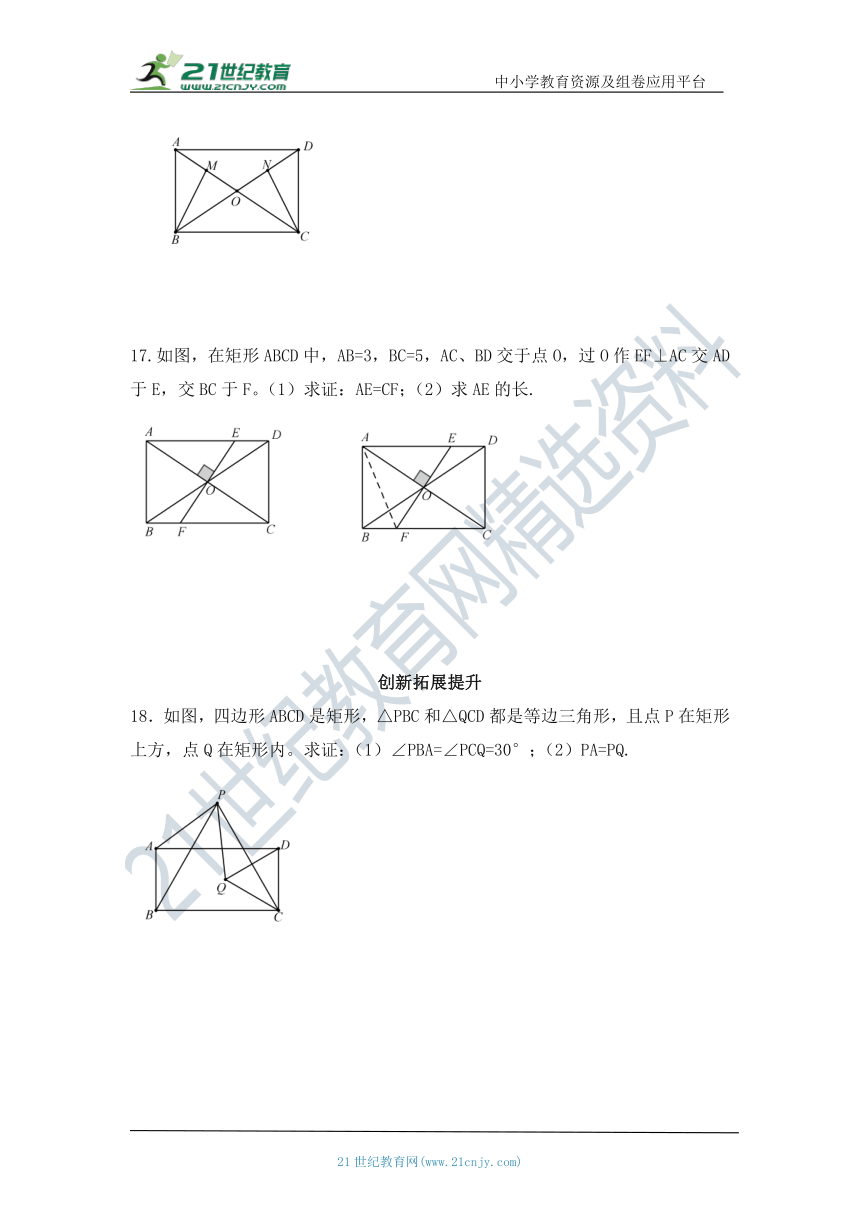
16.如图,矩形ABCD中,对角线AC、BD相交于O点,M、N分别为OA、OD的中点,求证:BM=CN.
17.如图,在矩形ABCD中,AB=3,BC=5,AC、BD交于点O,过O作EF⊥AC交AD于E,交BC于F。(1)求证:AE=CF;(2)求AE的长.
创新拓展提升
18.如图,四边形ABCD是矩形,△PBC和△QCD都是等边三角形,且点P在矩形上方,点Q在矩形内。求证:(1)∠PBA=∠PCQ=30°;(2)PA=PQ.
18.2.1矩形(第1课时)
A双基导学导练
知识点1 矩形是一个角是直角的平行四边形,具有平行四边形的性质,还具有四个角是直角,对角线相等的性质
1.如图,矩形ABCD中,ABA.2个 B.4个 C.6个 D.8个
答案:B
2.矩形的周长为22cm,一条边长为7cm,则另一条边长为__________,面积为__________
答案:4cm 28cm
3.矩形ABCD中,对角线AC、BD相交于点O,AB=8,BC=6,则对角线AC的长为_________,AO的长为____________
答案:10 5
4.如图,在矩形ABCD中,对角线AC、BD相交于点O,∠AOB=60°,AB=4,则BC=_______
答案:8
5.矩形的对角线相交所成的锐角是60°,短边的长为3cm,则对角线的长为______,长边的长为________________
答案:6cm 3false
6.如图,在△ABC中,∠ABC=90°,D是AC的中点,若∠A=25°,则∠BDC=_______,∠CBD=__________
答案:50° 65°
知识点2 直角三角形斜边上的中线等于斜边的一半
7.直角三角形中,两直角边分别是6和8,则斜边上的中线是______________
答案:5
8.如图,矩形ABCD中,若AD=1,AB=false,则DO=_________,∠DOA的度数是________
答案:1 60°
9.如图,矩形ABCD中,AB=3cm,AE平分∠BAD交BC于E,则AE的长是__________cm
答案:3false
10.如图,在△ABC中,∠ACB=90°,M、N分别是AB、AC的中点,延长BC至点D,使CD=falseBD,连接DM、DN,MN,若AB=6,则DN=_____________
答案:3
B真题检测反馈
11.矩形具有而平行四边形不一定具有的性质是( )
A.对边相等 B.对角相等 C.对角互补 D.对角线互相平分
答案:C
12.如图,矩形ABCD中,BE⊥AC于E,DF⊥AC于F,若AE=2,EF=3,则AC=_________
答案:7
13.如图,矩形ABCD中,AE⊥BD于E,且∠BAE=false∠DAE,则∠ABO=_____,∠CAE=____
答案:∠ABO=67.5°,∠CAE=45°
14.在Rt△ABC中,CD是斜边AB上的中线,且CD=5,则AB2+BC2+AC2=_____
答案:200
15.如图,矩形ABCD中,点M是BC上一点,AM=AD,DN⊥AM于N,连接DM.下列结论:①∠DMC=∠ADM=∠AMD;②△AND≌△MAB;③AN+CM=BC;④∠MDC=false∠AMB.其中正确的有( )
A.1个 B.2个 C.3个 D.4个
答案:D
16.如图,矩形ABCD中,对角线AC、BD相交于O点,M、N分别为OA、OD的中点,求证:BM=CN.
证明:OB=OC,OM=ON,△BOM≌△CON
17.如图,在矩形ABCD中,AB=3,BC=5,AC、BD交于点O,过O作EF⊥AC交AD于E,交BC于F。(1)求证:AE=CF;(2)求AE的长.
(1)证明:证△AOE≌△COF
(2)解:连接AF,由(1)知OE=OF,AC垂直平分EF
∴AE=AF=CF
设AE=x,则AF=x,BF=5-x
在△ABF中,32+(5-x)2=x2,x=false ∴AE=false
创新拓展提升
18.如图,四边形ABCD是矩形,△PBC和△QCD都是等边三角形,且点P在矩形上方,点Q在矩形内。求证:(1)∠PBA=∠PCQ=30°;(2)PA=PQ.
证明:(1)∵四边形ABCD是矩形,∴∠ABC=∠DCB=90°
∵ △PBC、△QCD是等边三角形 ∴ ∠PBC=∠QCD=60°
∴∠PBA=∠DCP=30° ∴∠PBA=∠PCQ=30°
(2)∵PB=PC AB=CD=CQ ∴△PAB≌△PQC ∴PA=PQ
A双基导学导练
知识点1 矩形是一个角是直角的平行四边形,具有平行四边形的性质,还具有四个角是直角,对角线相等的性质
如图,矩形ABCD中,AB
2.矩形的周长为22cm,一条边长为7cm,则另一条边长为__________,面积为__________
3.矩形ABCD中,对角线AC、BD相交于点O,AB=8,BC=6,则对角线AC的长为_________,AO的长为____________
4.如图,在矩形ABCD中,对角线AC、BD相交于点O,∠AOB=60°,AB=4,则BC=_______
5.矩形的对角线相交所成的锐角是60°,短边的长为3cm,则对角线的长为______,长边的长为________________
6.如图,在△ABC中,∠ABC=90°,D是AC的中点,若∠A=25°,则∠BDC=_______,∠CBD=__________
知识点2 直角三角形斜边上的中线等于斜边的一半
7.直角三角形中,两直角边分别是6和8,则斜边上的中线是______________
8.如图,矩形ABCD中,若AD=1,AB=false,则DO=_________,∠DOA的度数是________
9.如图,矩形ABCD中,AB=3cm,AE平分∠BAD交BC于E,则AE的长是__________cm
10.如图,在△ABC中,∠ACB=90°,M、N分别是AB、AC的中点,延长BC至点D,使CD=falseBD,连接DM、DN,MN,若AB=6,则DN=_____________
B真题检测反馈
11.矩形具有而平行四边形不一定具有的性质是( )
A.对边相等 B.对角相等 C.对角互补 D.对角线互相平分
12.如图,矩形ABCD中,BE⊥AC于E,DF⊥AC于F,若AE=2,EF=3,则AC=_________
13.如图,矩形ABCD中,AE⊥BD于E,且∠BAE=false∠DAE,则∠ABO=_____,∠CAE=____
14.在Rt△ABC中,CD是斜边AB上的中线,且CD=5,则AB2+BC2+AC2=_____
15.如图,矩形ABCD中,点M是BC上一点,AM=AD,DN⊥AM于N,连接DM.下列结论:①∠DMC=∠ADM=∠AMD;②△AND≌△MAB;③AN+CM=BC;④∠MDC=false∠AMB.其中正确的有( )
A.1个 B.2个 C.3个 D.4个
16.如图,矩形ABCD中,对角线AC、BD相交于O点,M、N分别为OA、OD的中点,求证:BM=CN.
17.如图,在矩形ABCD中,AB=3,BC=5,AC、BD交于点O,过O作EF⊥AC交AD于E,交BC于F。(1)求证:AE=CF;(2)求AE的长.
创新拓展提升
18.如图,四边形ABCD是矩形,△PBC和△QCD都是等边三角形,且点P在矩形上方,点Q在矩形内。求证:(1)∠PBA=∠PCQ=30°;(2)PA=PQ.
18.2.1矩形(第1课时)
A双基导学导练
知识点1 矩形是一个角是直角的平行四边形,具有平行四边形的性质,还具有四个角是直角,对角线相等的性质
1.如图,矩形ABCD中,AB
答案:B
2.矩形的周长为22cm,一条边长为7cm,则另一条边长为__________,面积为__________
答案:4cm 28cm
3.矩形ABCD中,对角线AC、BD相交于点O,AB=8,BC=6,则对角线AC的长为_________,AO的长为____________
答案:10 5
4.如图,在矩形ABCD中,对角线AC、BD相交于点O,∠AOB=60°,AB=4,则BC=_______
答案:8
5.矩形的对角线相交所成的锐角是60°,短边的长为3cm,则对角线的长为______,长边的长为________________
答案:6cm 3false
6.如图,在△ABC中,∠ABC=90°,D是AC的中点,若∠A=25°,则∠BDC=_______,∠CBD=__________
答案:50° 65°
知识点2 直角三角形斜边上的中线等于斜边的一半
7.直角三角形中,两直角边分别是6和8,则斜边上的中线是______________
答案:5
8.如图,矩形ABCD中,若AD=1,AB=false,则DO=_________,∠DOA的度数是________
答案:1 60°
9.如图,矩形ABCD中,AB=3cm,AE平分∠BAD交BC于E,则AE的长是__________cm
答案:3false
10.如图,在△ABC中,∠ACB=90°,M、N分别是AB、AC的中点,延长BC至点D,使CD=falseBD,连接DM、DN,MN,若AB=6,则DN=_____________
答案:3
B真题检测反馈
11.矩形具有而平行四边形不一定具有的性质是( )
A.对边相等 B.对角相等 C.对角互补 D.对角线互相平分
答案:C
12.如图,矩形ABCD中,BE⊥AC于E,DF⊥AC于F,若AE=2,EF=3,则AC=_________
答案:7
13.如图,矩形ABCD中,AE⊥BD于E,且∠BAE=false∠DAE,则∠ABO=_____,∠CAE=____
答案:∠ABO=67.5°,∠CAE=45°
14.在Rt△ABC中,CD是斜边AB上的中线,且CD=5,则AB2+BC2+AC2=_____
答案:200
15.如图,矩形ABCD中,点M是BC上一点,AM=AD,DN⊥AM于N,连接DM.下列结论:①∠DMC=∠ADM=∠AMD;②△AND≌△MAB;③AN+CM=BC;④∠MDC=false∠AMB.其中正确的有( )
A.1个 B.2个 C.3个 D.4个
答案:D
16.如图,矩形ABCD中,对角线AC、BD相交于O点,M、N分别为OA、OD的中点,求证:BM=CN.
证明:OB=OC,OM=ON,△BOM≌△CON
17.如图,在矩形ABCD中,AB=3,BC=5,AC、BD交于点O,过O作EF⊥AC交AD于E,交BC于F。(1)求证:AE=CF;(2)求AE的长.
(1)证明:证△AOE≌△COF
(2)解:连接AF,由(1)知OE=OF,AC垂直平分EF
∴AE=AF=CF
设AE=x,则AF=x,BF=5-x
在△ABF中,32+(5-x)2=x2,x=false ∴AE=false
创新拓展提升
18.如图,四边形ABCD是矩形,△PBC和△QCD都是等边三角形,且点P在矩形上方,点Q在矩形内。求证:(1)∠PBA=∠PCQ=30°;(2)PA=PQ.
证明:(1)∵四边形ABCD是矩形,∴∠ABC=∠DCB=90°
∵ △PBC、△QCD是等边三角形 ∴ ∠PBC=∠QCD=60°
∴∠PBA=∠DCP=30° ∴∠PBA=∠PCQ=30°
(2)∵PB=PC AB=CD=CQ ∴△PAB≌△PQC ∴PA=PQ
