18.2.1 矩形(第2课时) 知识点导学导练+检测(含答案)
文档属性
| 名称 | 18.2.1 矩形(第2课时) 知识点导学导练+检测(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 112.7KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-04-19 18:19:45 | ||
图片预览


文档简介
18.2.1 矩形(第2课时)
A 双基导学导练
知识点1 有一个角是直角的平行四边形是矩形
1.四边形ABCD中,AD∥BC,且AD=BC,当∠A=___________时,四边形ABCD是矩形.
2.如图,DE∥AB,DF∥AC,∠B=50°,当∠C=_____时,四边形AFDE是矩形
3.如图,要使□ABCD成为矩形,需添加的条件是( )
A.AB=BC B.AC⊥BD C.∠ABC=90° D.∠1=∠2
知识点2 对角线相等的平行四边形是矩形
4.已知四边形ABCD的对角线互相平分,要使它变为矩形,需要添加的条件是( )
A.AB=CD B.∠ABD=∠CBD C.AB=BC D.AC=BD
5.如图,在□ABCD中,若∠1=∠2,则四边形ABCD是________
6.矩形的面积为12cm2,一条边长为4cm,则另一边长为______cm,周长为_______cm
7.矩形ABCD中,对角线AC、BD交于点O,∠AOB=60°,若BD=10cm,则AB=_____cm,AD=____cm
知识点3 有三个角是直角的四边形是矩形
8.下列说法:①有一个角是直角的四边形是矩形;②有两个角是直角的四边形是矩形;③有三个角是直角的四边形是矩形;④四个角都相等的四边形是矩形.其中,正确的是( )
A. ①② B. ③② C. ③④ D. ①④
9.下列命题,正确的是( )
A.有一个角是直角的四边形是矩形 B.三个角是直角的多边形是矩形
C.两条对角线相等的四边形是矩形 D.两条对角线相等的平行四边形是矩形
10.直角三角形斜边上的高与中线分别是4cm和6cm,则它的面积是_______cm2
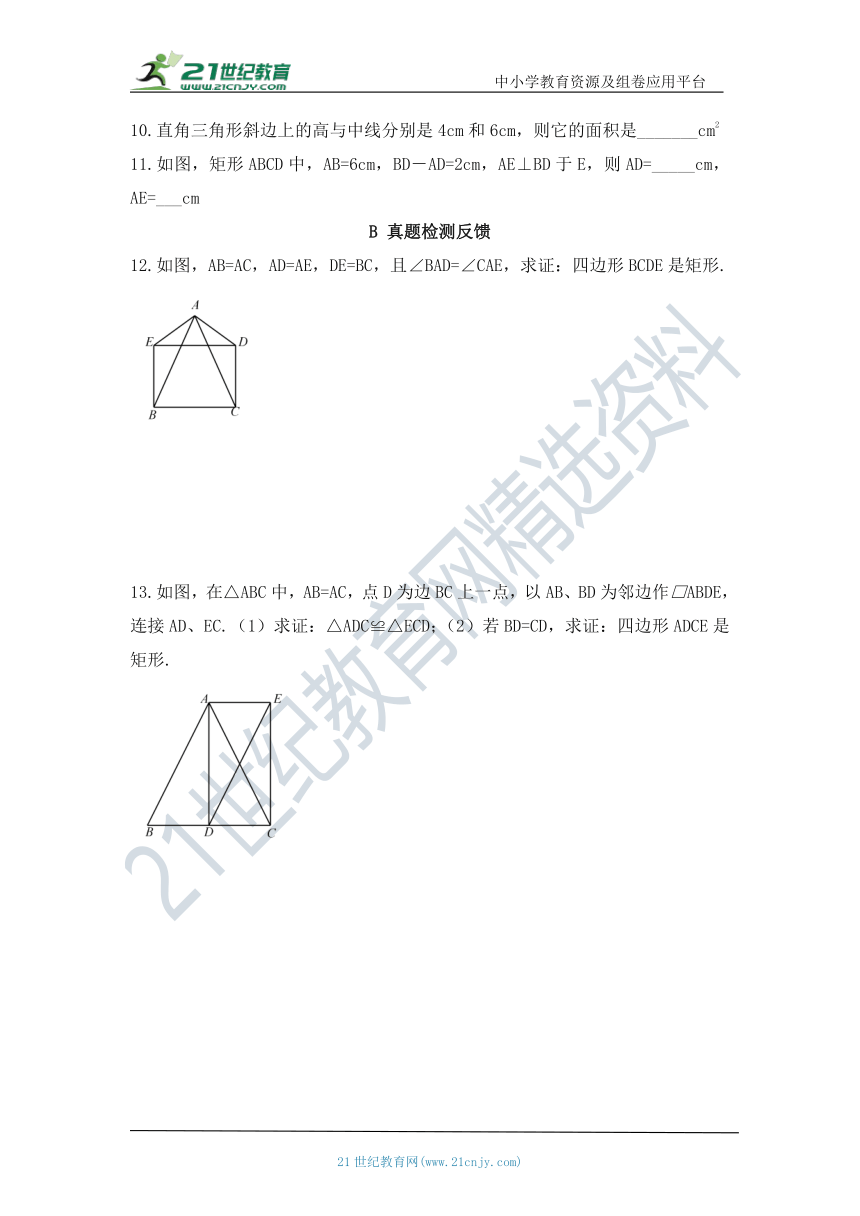
11.如图,矩形ABCD中,AB=6cm,BD-AD=2cm,AE⊥BD于E,则AD=_____cm,AE=___cm
B 真题检测反馈
12.如图,AB=AC,AD=AE,DE=BC,且∠BAD=∠CAE,求证:四边形BCDE是矩形.
13.如图,在△ABC中,AB=AC,点D为边BC上一点,以AB、BD为邻边作□ABDE,连接AD、EC.(1)求证:△ADC≌△ECD;(2)若BD=CD,求证:四边形ADCE是矩形.
14.如图,□ABCD四个内角的角平分线分别交于点E、F、G、H.求证:四边形EFGH是矩形
15.如图,□ABCD中,对角线AC、BD交于点O,过O作EF⊥AC,分别交AB、CD于E、F,且BE=OE=falseAE,求证:□ABCD是矩形
C.创新拓展提升
16.如图,在矩形ABCD中,AB=6,AD=8,P、E分别是线段AC、BC上的点,且四边形PEFD为矩形,(1)若△PCD是等腰三角形时,求AP的长;(2)求证:PC⊥CF.
18.2.1 矩形(第2课时)
A 双基导学导练
知识点1 有一个角是直角的平行四边形是矩形
1.四边形ABCD中,AD∥BC,且AD=BC,当∠A=___________时,四边形ABCD是矩形.
答案:90°
2.如图,DE∥AB,DF∥AC,∠B=50°,当∠C=_____时,四边形AFDE是矩形
答案:40°
3.如图,要使□ABCD成为矩形,需添加的条件是( )
A.AB=BC B.AC⊥BD C.∠ABC=90° D.∠1=∠2
答案:C
知识点2 对角线相等的平行四边形是矩形
4.已知四边形ABCD的对角线互相平分,要使它变为矩形,需要添加的条件是( )
A.AB=CD B.∠ABD=∠CBD C.AB=BC D.AC=BD
答案:D
5.如图,在□ABCD中,若∠1=∠2,则四边形ABCD是________
答案:矩形
6.矩形的面积为12cm2,一条边长为4cm,则另一边长为______cm,周长为_______cm
答案:3 14
7.矩形ABCD中,对角线AC、BD交于点O,∠AOB=60°,若BD=10cm,则AB=_____cm,AD=____cm
答案:5 5false
知识点3 有三个角是直角的四边形是矩形
8.下列说法:①有一个角是直角的四边形是矩形;②有两个角是直角的四边形是矩形;③有三个角是直角的四边形是矩形;④四个角都相等的四边形是矩形.其中,正确的是( )
A. ①② B. ③② C. ③④ D. ①④
答案:C
9.下列命题,正确的是( )
A.有一个角是直角的四边形是矩形 B.三个角是直角的多边形是矩形
C.两条对角线相等的四边形是矩形 D.两条对角线相等的平行四边形是矩形
答案:D
10.直角三角形斜边上的高与中线分别是4cm和6cm,则它的面积是_______cm2
答案:24
11.如图,矩形ABCD中,AB=6cm,BD-AD=2cm,AE⊥BD于E,则AD=_____cm,AE=___cm
答案:8 4.8
B 真题检测反馈
12.如图,AB=AC,AD=AE,DE=BC,且∠BAD=∠CAE,求证:四边形BCDE是矩形.
证明:∵ △AEB≌△ADC ∴BE=DC,∠AEB=∠ADC
又∵ AE=AD,DE=BC
∴ ∠AED=∠ADE,四边形BCDE为平行四边形
∴ ∠DEB=∠EDC
∴ 四边形BCDE为矩形
13.如图,在△ABC中,AB=AC,点D为边BC上一点,以AB、BD为邻边作□ABDE,连接AD、EC.(1)求证:△ADC≌△ECD;(2)若BD=CD,求证:四边形ADCE是矩形.
证明:(1)∵AB∥DE ∴∠B=∠ACD=∠EDC
又 ∵ AC=AB=ED ∴ △ADC≌△ECD
(2)∵ BD=CD ∴ AD⊥DC,BD=DC=AE
又∵ BC∥AE ∴ 四边形ADCE为矩形
14.如图,□ABCD四个内角的角平分线分别交于点E、F、G、H.求证:四边形EFGH是矩形
证明:∠HEF=∠F=∠H=90°
15.如图,□ABCD中,对角线AC、BD交于点O,过O作EF⊥AC,分别交AB、CD于E、F,且BE=OE=falseAE,求证:□ABCD是矩形
证明:连接AF,证△BOE≌△DOF得OE=0F=falseAE,则EF=AE,
∴EF=AE=AF 得△AEF是正三角形 ∴∠AEO=60°,
∴∠EAO=30°,由BE=OE得∠OBE=30°,
∴∠OAB=∠OBA ∴OA=OB
从而可得矩形ABCD.
C.创新拓展提升
16.如图,在矩形ABCD中,AB=6,AD=8,P、E分别是线段AC、BC上的点,且四边形PEFD为矩形,(1)若△PCD是等腰三角形时,求AP的长;(2)求证:PC⊥CF.
(1)解:在矩形ABCD中,AB=6,AD=8,∠ADC=90°
∴DC=AB=6,AC=false=10
要使△PCD是等腰三角形,有如下三种情况:
当CP=CD时,CP=6,∴AP=AC-CP=4
当PD=PC时,∠PDC=∠PCD,∵∠PCD+∠PAD=∠PDC+∠PDA=90°
∴∠PAD=∠PDA,∴PD=PA ∴PA=PC ∴AP=false即AP=5
当DP=DC时,过D作DQ⊥AC于Q,则PQ=CQ,∵S△ADC=falseAD·DC=falseAC·DQ
∴DQ=false,∴CQ=false,∴PC=2CQ=false,
∴AP=AC-PC=false
综上所述,若△PCD是等腰三角形,AP的长为4或5或false
(2)证明:连接PF、DE,记PF与DE的交点为O,连接OC
∵ 四边形ABCD是矩形 ∴∠BCD=90°,OE=OD,∴OC=falseED
在矩形PEFD中,PF=DE,∵OC=falsePF,∴OP=OF=falsePF,∵OC=OP=OF
∴∠OCF=∠OFC,∠OCP=∠OPC又 ∵∠OPC+∠OFC+∠PCF=180°
∴ 2∠OCP+2∠OCF=180° ∴∠PCF=90°。
A 双基导学导练
知识点1 有一个角是直角的平行四边形是矩形
1.四边形ABCD中,AD∥BC,且AD=BC,当∠A=___________时,四边形ABCD是矩形.
2.如图,DE∥AB,DF∥AC,∠B=50°,当∠C=_____时,四边形AFDE是矩形
3.如图,要使□ABCD成为矩形,需添加的条件是( )
A.AB=BC B.AC⊥BD C.∠ABC=90° D.∠1=∠2
知识点2 对角线相等的平行四边形是矩形
4.已知四边形ABCD的对角线互相平分,要使它变为矩形,需要添加的条件是( )
A.AB=CD B.∠ABD=∠CBD C.AB=BC D.AC=BD
5.如图,在□ABCD中,若∠1=∠2,则四边形ABCD是________
6.矩形的面积为12cm2,一条边长为4cm,则另一边长为______cm,周长为_______cm
7.矩形ABCD中,对角线AC、BD交于点O,∠AOB=60°,若BD=10cm,则AB=_____cm,AD=____cm
知识点3 有三个角是直角的四边形是矩形
8.下列说法:①有一个角是直角的四边形是矩形;②有两个角是直角的四边形是矩形;③有三个角是直角的四边形是矩形;④四个角都相等的四边形是矩形.其中,正确的是( )
A. ①② B. ③② C. ③④ D. ①④
9.下列命题,正确的是( )
A.有一个角是直角的四边形是矩形 B.三个角是直角的多边形是矩形
C.两条对角线相等的四边形是矩形 D.两条对角线相等的平行四边形是矩形
10.直角三角形斜边上的高与中线分别是4cm和6cm,则它的面积是_______cm2
11.如图,矩形ABCD中,AB=6cm,BD-AD=2cm,AE⊥BD于E,则AD=_____cm,AE=___cm
B 真题检测反馈
12.如图,AB=AC,AD=AE,DE=BC,且∠BAD=∠CAE,求证:四边形BCDE是矩形.
13.如图,在△ABC中,AB=AC,点D为边BC上一点,以AB、BD为邻边作□ABDE,连接AD、EC.(1)求证:△ADC≌△ECD;(2)若BD=CD,求证:四边形ADCE是矩形.
14.如图,□ABCD四个内角的角平分线分别交于点E、F、G、H.求证:四边形EFGH是矩形
15.如图,□ABCD中,对角线AC、BD交于点O,过O作EF⊥AC,分别交AB、CD于E、F,且BE=OE=falseAE,求证:□ABCD是矩形
C.创新拓展提升
16.如图,在矩形ABCD中,AB=6,AD=8,P、E分别是线段AC、BC上的点,且四边形PEFD为矩形,(1)若△PCD是等腰三角形时,求AP的长;(2)求证:PC⊥CF.
18.2.1 矩形(第2课时)
A 双基导学导练
知识点1 有一个角是直角的平行四边形是矩形
1.四边形ABCD中,AD∥BC,且AD=BC,当∠A=___________时,四边形ABCD是矩形.
答案:90°
2.如图,DE∥AB,DF∥AC,∠B=50°,当∠C=_____时,四边形AFDE是矩形
答案:40°
3.如图,要使□ABCD成为矩形,需添加的条件是( )
A.AB=BC B.AC⊥BD C.∠ABC=90° D.∠1=∠2
答案:C
知识点2 对角线相等的平行四边形是矩形
4.已知四边形ABCD的对角线互相平分,要使它变为矩形,需要添加的条件是( )
A.AB=CD B.∠ABD=∠CBD C.AB=BC D.AC=BD
答案:D
5.如图,在□ABCD中,若∠1=∠2,则四边形ABCD是________
答案:矩形
6.矩形的面积为12cm2,一条边长为4cm,则另一边长为______cm,周长为_______cm
答案:3 14
7.矩形ABCD中,对角线AC、BD交于点O,∠AOB=60°,若BD=10cm,则AB=_____cm,AD=____cm
答案:5 5false
知识点3 有三个角是直角的四边形是矩形
8.下列说法:①有一个角是直角的四边形是矩形;②有两个角是直角的四边形是矩形;③有三个角是直角的四边形是矩形;④四个角都相等的四边形是矩形.其中,正确的是( )
A. ①② B. ③② C. ③④ D. ①④
答案:C
9.下列命题,正确的是( )
A.有一个角是直角的四边形是矩形 B.三个角是直角的多边形是矩形
C.两条对角线相等的四边形是矩形 D.两条对角线相等的平行四边形是矩形
答案:D
10.直角三角形斜边上的高与中线分别是4cm和6cm,则它的面积是_______cm2
答案:24
11.如图,矩形ABCD中,AB=6cm,BD-AD=2cm,AE⊥BD于E,则AD=_____cm,AE=___cm
答案:8 4.8
B 真题检测反馈
12.如图,AB=AC,AD=AE,DE=BC,且∠BAD=∠CAE,求证:四边形BCDE是矩形.
证明:∵ △AEB≌△ADC ∴BE=DC,∠AEB=∠ADC
又∵ AE=AD,DE=BC
∴ ∠AED=∠ADE,四边形BCDE为平行四边形
∴ ∠DEB=∠EDC
∴ 四边形BCDE为矩形
13.如图,在△ABC中,AB=AC,点D为边BC上一点,以AB、BD为邻边作□ABDE,连接AD、EC.(1)求证:△ADC≌△ECD;(2)若BD=CD,求证:四边形ADCE是矩形.
证明:(1)∵AB∥DE ∴∠B=∠ACD=∠EDC
又 ∵ AC=AB=ED ∴ △ADC≌△ECD
(2)∵ BD=CD ∴ AD⊥DC,BD=DC=AE
又∵ BC∥AE ∴ 四边形ADCE为矩形
14.如图,□ABCD四个内角的角平分线分别交于点E、F、G、H.求证:四边形EFGH是矩形
证明:∠HEF=∠F=∠H=90°
15.如图,□ABCD中,对角线AC、BD交于点O,过O作EF⊥AC,分别交AB、CD于E、F,且BE=OE=falseAE,求证:□ABCD是矩形
证明:连接AF,证△BOE≌△DOF得OE=0F=falseAE,则EF=AE,
∴EF=AE=AF 得△AEF是正三角形 ∴∠AEO=60°,
∴∠EAO=30°,由BE=OE得∠OBE=30°,
∴∠OAB=∠OBA ∴OA=OB
从而可得矩形ABCD.
C.创新拓展提升
16.如图,在矩形ABCD中,AB=6,AD=8,P、E分别是线段AC、BC上的点,且四边形PEFD为矩形,(1)若△PCD是等腰三角形时,求AP的长;(2)求证:PC⊥CF.
(1)解:在矩形ABCD中,AB=6,AD=8,∠ADC=90°
∴DC=AB=6,AC=false=10
要使△PCD是等腰三角形,有如下三种情况:
当CP=CD时,CP=6,∴AP=AC-CP=4
当PD=PC时,∠PDC=∠PCD,∵∠PCD+∠PAD=∠PDC+∠PDA=90°
∴∠PAD=∠PDA,∴PD=PA ∴PA=PC ∴AP=false即AP=5
当DP=DC时,过D作DQ⊥AC于Q,则PQ=CQ,∵S△ADC=falseAD·DC=falseAC·DQ
∴DQ=false,∴CQ=false,∴PC=2CQ=false,
∴AP=AC-PC=false
综上所述,若△PCD是等腰三角形,AP的长为4或5或false
(2)证明:连接PF、DE,记PF与DE的交点为O,连接OC
∵ 四边形ABCD是矩形 ∴∠BCD=90°,OE=OD,∴OC=falseED
在矩形PEFD中,PF=DE,∵OC=falsePF,∴OP=OF=falsePF,∵OC=OP=OF
∴∠OCF=∠OFC,∠OCP=∠OPC又 ∵∠OPC+∠OFC+∠PCF=180°
∴ 2∠OCP+2∠OCF=180° ∴∠PCF=90°。
