18.2.2 菱形 (第2课时)知识点导学导练+检测(含答案)
文档属性
| 名称 | 18.2.2 菱形 (第2课时)知识点导学导练+检测(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 123.5KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-04-19 18:24:10 | ||
图片预览


文档简介
18.2.2 菱形 (第2课时)
A双基导学导练
知识点1: 利用菱形的定义判定菱形
1.如图,要使□ABCD为菱形,则需添加的一个条件是( )
A.?AB=?AC B.AB⊥BC C.?AC=BD D?.AB=?AD
2.如图,△ABC中,D是AB上一点,?DE∥AC交BC于E,DF∥BC交AC于F,下列条件:①∠ACB=90°;②CD平分∠ACB;③AC=BC,AD=BD.从中选择一个条件使四边形DECF是菱形,则这个条件是 (只填序号).
3.如图,点E,F,G,H分别是四边形ABCD中AD,BD,BC,CA的中点,当四边形ABCD满足条件( )时,四边形EFGH是菱形.
A.?AB=AD B.?AC=?BD C.AB=?CD D. AC⊥BD
知识点2. 有一组邻边相等的平行四边形是菱形;四边相等的四边形是菱形
4.已知,四边形ABCD是平行四边形,则下列结论中不正确的是( )
A.AB=CD B.当AC⊥BD时,它是菱形
C.AC=?BD D.当∠ABC=90°时,它是矩形
5.如图,△ABC中,AD平分∠BAC,DE∥AC,DF∥AB,分别交AB、AC于E、F,求证:□AEDF为菱形
知识点3 对角线相互垂直平分的四边形是菱形
6.□ABCD的对角线AC、BD交于O,下列条件中,不能判定□ ABCD是菱形的是( )
A.?AB=AD B.AC⊥BD C.∠BAD=∠ADC D.CA平分∠BCD
7.如图,在菱形ABCD中,AB=5,∠BCD=120°,则对角线AC等于( )
A.20 B.15 C.10 D.5
菱形的对角线长为10和24,则菱形的周长为
9.菱形的一条对角线与边长相等,则菱形的两个邻角度数分别为 .
10.菱形的面积为50cm2,一个内角为30°,则其边长等于 .
B真题检测反馈
11.两个完全相同的矩形纸片ABCD、BFDE如图放置,AB=BF.求证:四边形BNDM为菱形
如图,矩形ABCD的对角线AC、BD相交于点O,DE∥CA,CE∥BD,连接OE.求证:OE⊥CD.
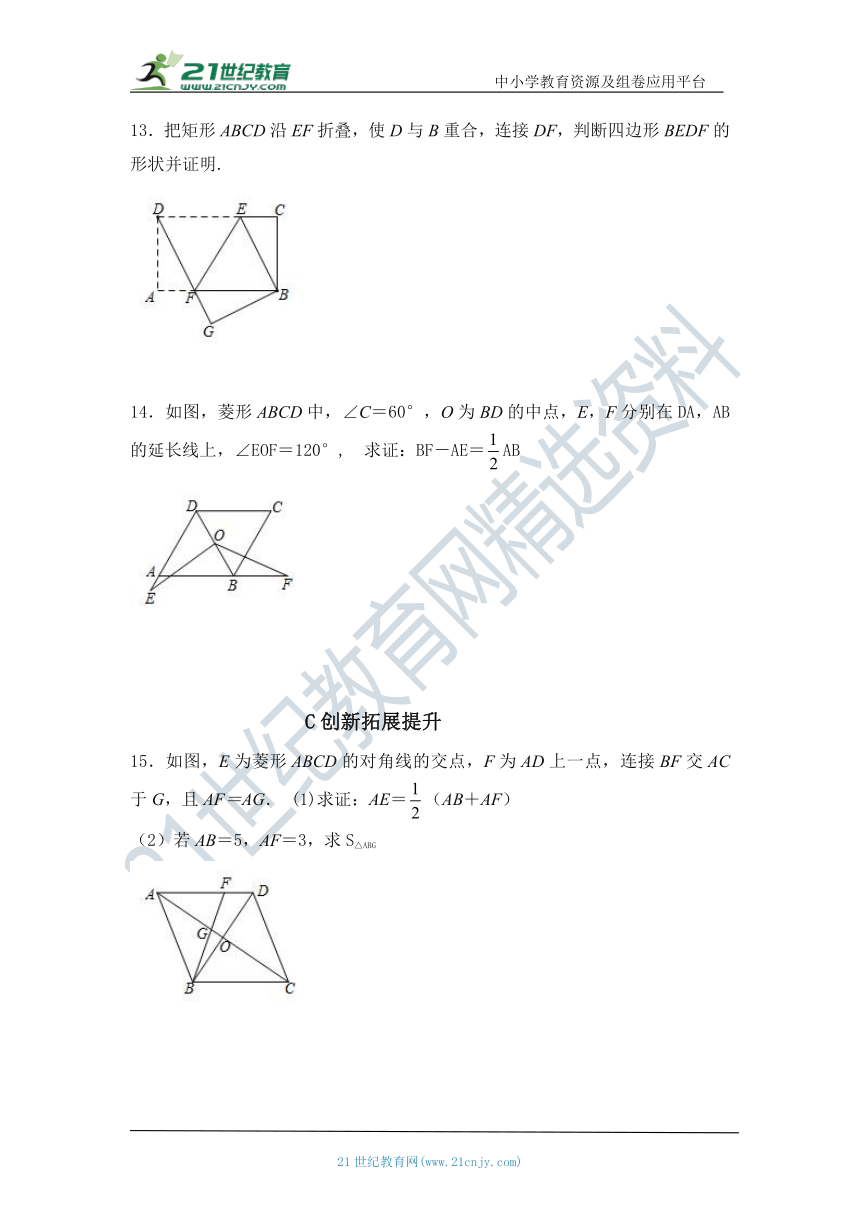
13.把矩形ABCD沿EF折叠,使D与B重合,连接DF,判断四边形BEDF的形状并证明.
14.如图,菱形ABCD中,∠C=60°,O为BD的中点,E,F分别在DA,AB的延长线上,∠EOF=120°, 求证:BF-AE=falseAB
C创新拓展提升
15.如图,E为菱形ABCD的对角线的交点,F为AD上一点,连接BF交AC于G,且AF=AG. (1)求证:AE=false(AB+AF)
(2)若AB=5,AF=3,求S△ABG
18.2.2 菱形 (第2课时)
A双基导学导练
知识点1: 利用菱形的定义判定菱形
1.如图,要使□ABCD为菱形,则需添加的一个条件是( )
A.?AB=?AC B.AB⊥BC C.?AC=BD D?.AB=?AD
答案:D
2.如图,△ABC中,D是AB上一点,?DE∥AC交BC于E,DF∥BC交AC于F,下列条件:①∠ACB=90°;②CD平分∠ACB;③AC=BC,AD=BD.从中选择一个条件使四边形DECF是菱形,则这个条件是 (只填序号).
答案:②或③
3.如图,点E,F,G,H分别是四边形ABCD中AD,BD,BC,CA的中点,当四边形ABCD满足条件( )时,四边形EFGH是菱形.
A.?AB=AD B.?AC=?BD C.AB=?CD D. AC⊥BD
答案:C
知识点2. 有一组邻边相等的平行四边形是菱形;四边相等的四边形是菱形
4.已知,四边形ABCD是平行四边形,则下列结论中不正确的是( )
A.AB=CD B.当AC⊥BD时,它是菱形
C.AC=?BD D.当∠ABC=90°时,它是矩形
答案:C
5.如图,△ABC中,AD平分∠BAC,DE∥AC,DF∥AB,分别交AB、AC于E、F,求证:□AEDF为菱形
答案:
证明:∵DE∥AC∴∠EDA=∠DAC=∠DAB ∴DE=?EA?∴□AEDF为菱形
知识点3 对角线相互垂直平分的四边形是菱形
6.□ABCD的对角线AC、BD交于O,下列条件中,不能判定□ ABCD是菱形的是( )
A.?AB=AD B.AC⊥BD C.∠BAD=∠ADC D.CA平分∠BCD
答案:C
7.如图,在菱形ABCD中,AB=5,∠BCD=120°,则对角线AC等于( )
A.20 B.15 C.10 D.5
答案:D
8.菱形的对角线长为10和24,则菱形的周长为
答案:52
9.菱形的一条对角线与边长相等,则菱形的两个邻角度数分别为 .
答案:60°,120°
10.菱形的面积为50cm2,一个内角为30°,则其边长等于 .
答案:10cm
B真题检测反馈
11.两个完全相同的矩形纸片ABCD、BFDE如图放置,AB=BF.求证:四边形BNDM为菱形
答案:
证明:∵四边形ABCD、BFDE是矩形∴∠A=∠ABN=∠MBF=∠BFN=90°
∴∠ABM=∠FBN∵AB=BF∴△ABM≌△FBN∴BN=BM
∵BM∥DN,?BN∥DM∴四边形BNDM是平行四边形 ∴□BNDM是菱形
12.如图,矩形ABCD的对角线AC、BD相交于点O,DE∥CA,CE∥BD,连接OE.求证:OE⊥CD.
答案:
证明:∵?DE∥OC,?CE∥OD∴四边形OCED为平行四边形∵四边形ABCD为矩形
∴OD=OC∴四边形OCED为菱形∴OE⊥CD
13.把矩形ABCD沿EF折叠,使D与B重合,连接DF,判断四边形BEDF的形状并证明.
答案:
证明:∵四边形ABCD是矩形 ∴CD∥AB,∠EFB=∠DEF=∠EFD∴DF=DE
又∵DF=BF,DE=EB ∴DF=BF= DE=EB ∴四边形BEDF是菱形
14.如图,菱形ABCD中,∠C=60°,O为BD的中点,E,F分别在DA,AB的延长线上,∠EOF=120°, 求证:BF-AE=falseAB
答案:
证明:取AD的中点M,连接OM,可证△OME≌△OBF
∴EM=BF∴BF?-AE=EM-AE=AM= falseAB
C创新拓展提升
15.如图,E为菱形ABCD的对角线的交点,F为AD上一点,连接BF交AC于G,且AF=AG. (1)求证:AE=false(AB+AF)
(2)若AB=5,AF=3,求S△ABG
答案:
(1)证明:∵AF=AG ∴∠AFG=∠FGA
∴∠BGC=∠CBG, ∴BC=CG=AB
∴AB+AF=CG+AG=AC=2AE, AE= false(AB+AF)
(2)解:∵AE=false(5+3)=4, ∴BE=3 ,∴SAB△G=falseAG?BE=false×3×3= false
A双基导学导练
知识点1: 利用菱形的定义判定菱形
1.如图,要使□ABCD为菱形,则需添加的一个条件是( )
A.?AB=?AC B.AB⊥BC C.?AC=BD D?.AB=?AD
2.如图,△ABC中,D是AB上一点,?DE∥AC交BC于E,DF∥BC交AC于F,下列条件:①∠ACB=90°;②CD平分∠ACB;③AC=BC,AD=BD.从中选择一个条件使四边形DECF是菱形,则这个条件是 (只填序号).
3.如图,点E,F,G,H分别是四边形ABCD中AD,BD,BC,CA的中点,当四边形ABCD满足条件( )时,四边形EFGH是菱形.
A.?AB=AD B.?AC=?BD C.AB=?CD D. AC⊥BD
知识点2. 有一组邻边相等的平行四边形是菱形;四边相等的四边形是菱形
4.已知,四边形ABCD是平行四边形,则下列结论中不正确的是( )
A.AB=CD B.当AC⊥BD时,它是菱形
C.AC=?BD D.当∠ABC=90°时,它是矩形
5.如图,△ABC中,AD平分∠BAC,DE∥AC,DF∥AB,分别交AB、AC于E、F,求证:□AEDF为菱形
知识点3 对角线相互垂直平分的四边形是菱形
6.□ABCD的对角线AC、BD交于O,下列条件中,不能判定□ ABCD是菱形的是( )
A.?AB=AD B.AC⊥BD C.∠BAD=∠ADC D.CA平分∠BCD
7.如图,在菱形ABCD中,AB=5,∠BCD=120°,则对角线AC等于( )
A.20 B.15 C.10 D.5
菱形的对角线长为10和24,则菱形的周长为
9.菱形的一条对角线与边长相等,则菱形的两个邻角度数分别为 .
10.菱形的面积为50cm2,一个内角为30°,则其边长等于 .
B真题检测反馈
11.两个完全相同的矩形纸片ABCD、BFDE如图放置,AB=BF.求证:四边形BNDM为菱形
如图,矩形ABCD的对角线AC、BD相交于点O,DE∥CA,CE∥BD,连接OE.求证:OE⊥CD.
13.把矩形ABCD沿EF折叠,使D与B重合,连接DF,判断四边形BEDF的形状并证明.
14.如图,菱形ABCD中,∠C=60°,O为BD的中点,E,F分别在DA,AB的延长线上,∠EOF=120°, 求证:BF-AE=falseAB
C创新拓展提升
15.如图,E为菱形ABCD的对角线的交点,F为AD上一点,连接BF交AC于G,且AF=AG. (1)求证:AE=false(AB+AF)
(2)若AB=5,AF=3,求S△ABG
18.2.2 菱形 (第2课时)
A双基导学导练
知识点1: 利用菱形的定义判定菱形
1.如图,要使□ABCD为菱形,则需添加的一个条件是( )
A.?AB=?AC B.AB⊥BC C.?AC=BD D?.AB=?AD
答案:D
2.如图,△ABC中,D是AB上一点,?DE∥AC交BC于E,DF∥BC交AC于F,下列条件:①∠ACB=90°;②CD平分∠ACB;③AC=BC,AD=BD.从中选择一个条件使四边形DECF是菱形,则这个条件是 (只填序号).
答案:②或③
3.如图,点E,F,G,H分别是四边形ABCD中AD,BD,BC,CA的中点,当四边形ABCD满足条件( )时,四边形EFGH是菱形.
A.?AB=AD B.?AC=?BD C.AB=?CD D. AC⊥BD
答案:C
知识点2. 有一组邻边相等的平行四边形是菱形;四边相等的四边形是菱形
4.已知,四边形ABCD是平行四边形,则下列结论中不正确的是( )
A.AB=CD B.当AC⊥BD时,它是菱形
C.AC=?BD D.当∠ABC=90°时,它是矩形
答案:C
5.如图,△ABC中,AD平分∠BAC,DE∥AC,DF∥AB,分别交AB、AC于E、F,求证:□AEDF为菱形
答案:
证明:∵DE∥AC∴∠EDA=∠DAC=∠DAB ∴DE=?EA?∴□AEDF为菱形
知识点3 对角线相互垂直平分的四边形是菱形
6.□ABCD的对角线AC、BD交于O,下列条件中,不能判定□ ABCD是菱形的是( )
A.?AB=AD B.AC⊥BD C.∠BAD=∠ADC D.CA平分∠BCD
答案:C
7.如图,在菱形ABCD中,AB=5,∠BCD=120°,则对角线AC等于( )
A.20 B.15 C.10 D.5
答案:D
8.菱形的对角线长为10和24,则菱形的周长为
答案:52
9.菱形的一条对角线与边长相等,则菱形的两个邻角度数分别为 .
答案:60°,120°
10.菱形的面积为50cm2,一个内角为30°,则其边长等于 .
答案:10cm
B真题检测反馈
11.两个完全相同的矩形纸片ABCD、BFDE如图放置,AB=BF.求证:四边形BNDM为菱形
答案:
证明:∵四边形ABCD、BFDE是矩形∴∠A=∠ABN=∠MBF=∠BFN=90°
∴∠ABM=∠FBN∵AB=BF∴△ABM≌△FBN∴BN=BM
∵BM∥DN,?BN∥DM∴四边形BNDM是平行四边形 ∴□BNDM是菱形
12.如图,矩形ABCD的对角线AC、BD相交于点O,DE∥CA,CE∥BD,连接OE.求证:OE⊥CD.
答案:
证明:∵?DE∥OC,?CE∥OD∴四边形OCED为平行四边形∵四边形ABCD为矩形
∴OD=OC∴四边形OCED为菱形∴OE⊥CD
13.把矩形ABCD沿EF折叠,使D与B重合,连接DF,判断四边形BEDF的形状并证明.
答案:
证明:∵四边形ABCD是矩形 ∴CD∥AB,∠EFB=∠DEF=∠EFD∴DF=DE
又∵DF=BF,DE=EB ∴DF=BF= DE=EB ∴四边形BEDF是菱形
14.如图,菱形ABCD中,∠C=60°,O为BD的中点,E,F分别在DA,AB的延长线上,∠EOF=120°, 求证:BF-AE=falseAB
答案:
证明:取AD的中点M,连接OM,可证△OME≌△OBF
∴EM=BF∴BF?-AE=EM-AE=AM= falseAB
C创新拓展提升
15.如图,E为菱形ABCD的对角线的交点,F为AD上一点,连接BF交AC于G,且AF=AG. (1)求证:AE=false(AB+AF)
(2)若AB=5,AF=3,求S△ABG
答案:
(1)证明:∵AF=AG ∴∠AFG=∠FGA
∴∠BGC=∠CBG, ∴BC=CG=AB
∴AB+AF=CG+AG=AC=2AE, AE= false(AB+AF)
(2)解:∵AE=false(5+3)=4, ∴BE=3 ,∴SAB△G=falseAG?BE=false×3×3= false
