三角形的中位线课件
图片预览



文档简介
(共20张PPT)
A
B
C
D
E
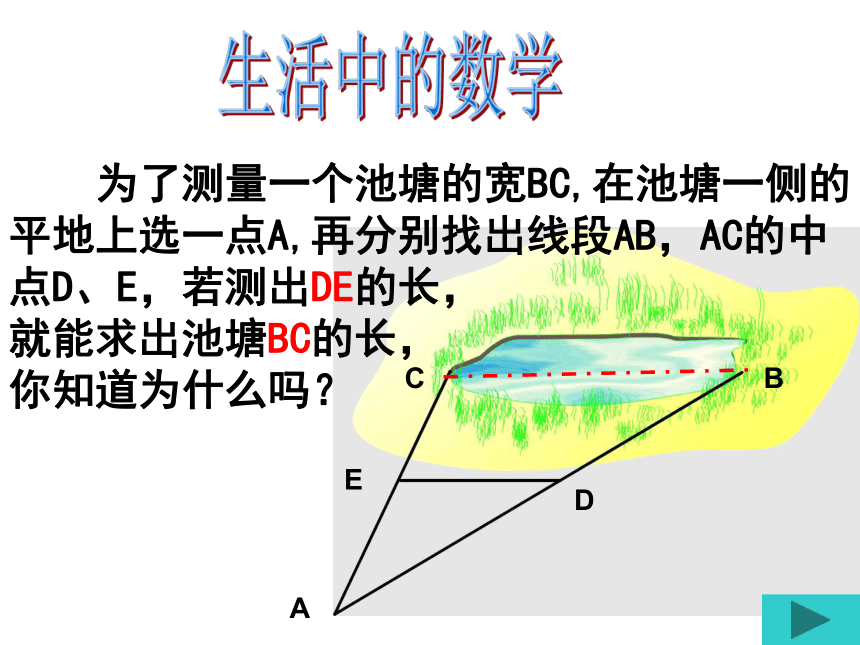
为了测量一个池塘的宽BC,在池塘一侧的平地上选一点A,再分别找出线段AB,AC的中点D、E,若测出DE的长,
就能求出池塘BC的长,
你知道为什么吗?
C
B
A
F
E
D
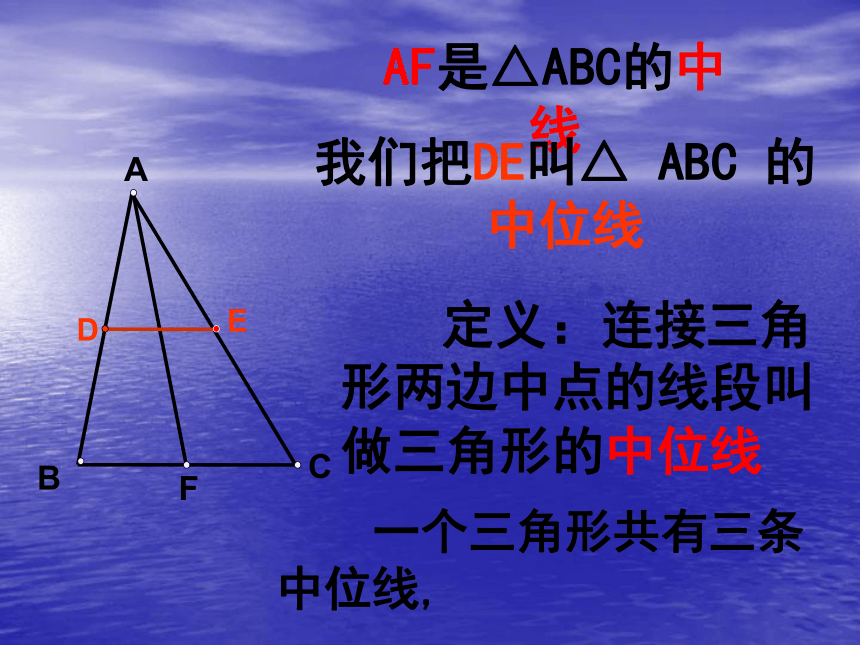
AF是△ABC的中线
我们把DE叫△ ABC 的中位线
定义:连接三角形两边中点的线段叫做三角形的中位线
一个三角形共有三条中位线,
中位线是连结两边中点的线段
中线是连结一个顶点和它的对边中点的线段
1.三角形的中位线和中线有什么不同呢
定义
2.三角形的中位线定义的两层含义:
(1) ∵D、E分别为AB、AC的中点
∴DE为△ABC的中位线
(2) ∵ DE为△ABC的中位线
∴ D、E分别为AB、AC的中点
C
B
A
E
D
F
三角形的中位线有什么性质?
如图,EF是△ABC 的一条中位线.
(1)量一量EF,BC的长是多少?你能作出什么猜测?
A
B
C
E
F
(2)观察图形中的EF与BC,猜测EF 与BC 位置关系吗?
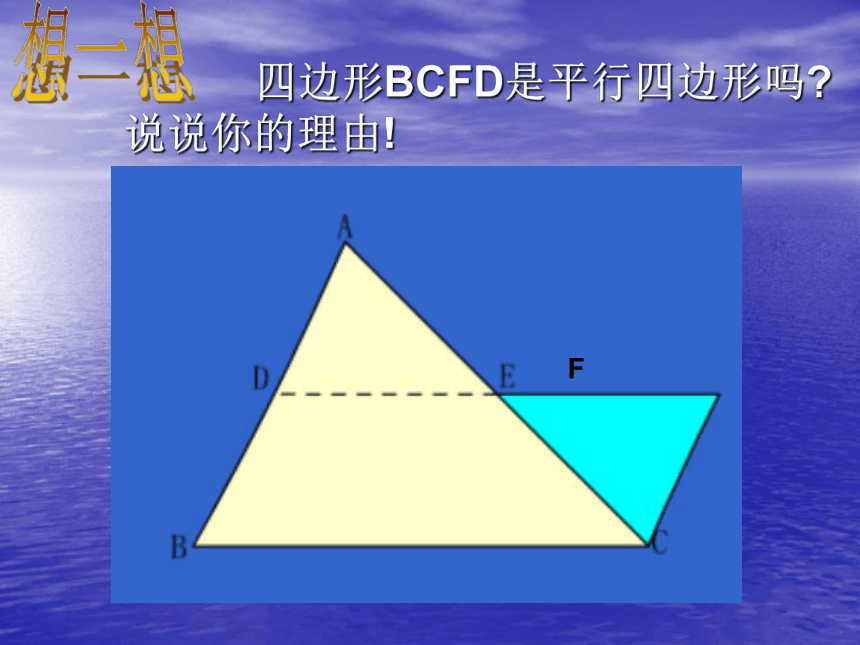
四边形BCFD是平行四边形吗 说说你的理由!
F
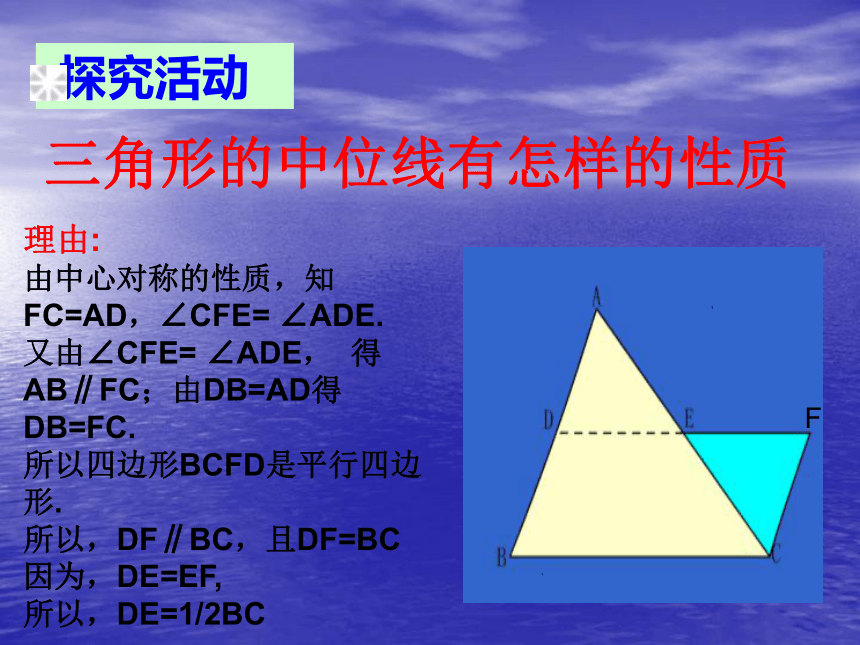
探究活动
三角形的中位线有怎样的性质
理由:
由中心对称的性质,知FC=AD,∠CFE= ∠ADE. 又由∠CFE= ∠ADE, 得AB∥FC;由DB=AD得DB=FC. 所以四边形BCFD是平行四边形.
所以,DF∥BC,且DF=BC
因为,DE=EF,
所以,DE=1/2BC
F
如图,如果 DE 是△ABC 的中位线,那么
⑴ DE∥BC, ⑵ DE= BC
(1)证明平行
(2)证明一条线段是另一条线
段的2倍或
A
B
C
D
E
三角形的中位线定理:三角形的中位线平行于第三边,并且等于第三边的一半.
2.定理的主要用途:
1.几何语言表示:
第三边
1.如图, MN 为△ABC 的中位线,若∠ABC =61°则∠AMN = ,
若MN =12 ,则BC = .
A
M
B
C
N
61°
24
[2007长沙中考] 如图, △ABC 中, D ,E 分别为AB,
AC 的中点,当BC =10㎝时,则DE = .
A
D
B
C
E
5㎝
3.如图,已知△ABC中,
AB = 3㎝,BC=3.4 ㎝ AC=4㎝ 且D,E,F分别为 AB,BC,AC边的中点,则△DEF的周长
是 ㎝.
A
B
C
D
E
F
5.2
如图,顺次连结四边形ABCD 各边中点E,F,H,M,得到的四边形EFHM 是平行四边形吗?为什么?
A
C
D
E
F
H
M
B
连结AC
所以:EF∥MH,且 EF=MH
所以:四边形EFHM是平行四边形.
解:
A
B
C
D
E
F
H
M
因为EF是△ABC的一条中位线,所以EF∥AC,且EF= AC
因为:MH 是△DAC 的一条中位线,
所以:MH∥AC,且 MH= AC
本节课你学到什么?
三角形的中位线平行于第三边,并且等于它的一半
连接三角形两边中点的线段叫做三角形的中位线
⑵已知:△ABC三边长分别为a,b,c,它的三条中位线组成△DEF,△DEF的三条中位线又组成△HPN,则△HPN的周长等于——————,为△ABC周长的——, 面积为△ABC面积的——,
⑴已知:三角形的各边分别为6cm,8cm, 10cm,则连结各边中点所成三角形的周长为——cm,面积为——cm2,为原三角形面积的——。
6
10
8
3
5
4
B
C
A
D
E
F
∠B —— ∠ADE(填“=”或“≠”)
=
H
P
N
⑷如图,AF=FD=DB,FG∥DE∥BC,PE=1.5,则DP= ———,BC= ———
3
4.5
9
1.5
P
A
B
F
G
E
C
D
如图,△ABC的边BC,CA,AB 的中点分别是D,E,F.
(1)四边形AFDE 是平行四边形吗 为什么
(2)四边形AFDE 的周长
等于AB+AC 吗
为什么
B
C
D
F
E
A
A
B
C
D
E
为了测量一个池塘的宽BC,在池塘一侧的平地上选一点A,再分别找出线段AB,AC的中点D、E,若测出DE的长,
就能求出池塘BC的长,
你知道为什么吗?
C
B
A
F
E
D
AF是△ABC的中线
我们把DE叫△ ABC 的中位线
定义:连接三角形两边中点的线段叫做三角形的中位线
一个三角形共有三条中位线,
中位线是连结两边中点的线段
中线是连结一个顶点和它的对边中点的线段
1.三角形的中位线和中线有什么不同呢
定义
2.三角形的中位线定义的两层含义:
(1) ∵D、E分别为AB、AC的中点
∴DE为△ABC的中位线
(2) ∵ DE为△ABC的中位线
∴ D、E分别为AB、AC的中点
C
B
A
E
D
F
三角形的中位线有什么性质?
如图,EF是△ABC 的一条中位线.
(1)量一量EF,BC的长是多少?你能作出什么猜测?
A
B
C
E
F
(2)观察图形中的EF与BC,猜测EF 与BC 位置关系吗?
四边形BCFD是平行四边形吗 说说你的理由!
F
探究活动
三角形的中位线有怎样的性质
理由:
由中心对称的性质,知FC=AD,∠CFE= ∠ADE. 又由∠CFE= ∠ADE, 得AB∥FC;由DB=AD得DB=FC. 所以四边形BCFD是平行四边形.
所以,DF∥BC,且DF=BC
因为,DE=EF,
所以,DE=1/2BC
F
如图,如果 DE 是△ABC 的中位线,那么
⑴ DE∥BC, ⑵ DE= BC
(1)证明平行
(2)证明一条线段是另一条线
段的2倍或
A
B
C
D
E
三角形的中位线定理:三角形的中位线平行于第三边,并且等于第三边的一半.
2.定理的主要用途:
1.几何语言表示:
第三边
1.如图, MN 为△ABC 的中位线,若∠ABC =61°则∠AMN = ,
若MN =12 ,则BC = .
A
M
B
C
N
61°
24
[2007长沙中考] 如图, △ABC 中, D ,E 分别为AB,
AC 的中点,当BC =10㎝时,则DE = .
A
D
B
C
E
5㎝
3.如图,已知△ABC中,
AB = 3㎝,BC=3.4 ㎝ AC=4㎝ 且D,E,F分别为 AB,BC,AC边的中点,则△DEF的周长
是 ㎝.
A
B
C
D
E
F
5.2
如图,顺次连结四边形ABCD 各边中点E,F,H,M,得到的四边形EFHM 是平行四边形吗?为什么?
A
C
D
E
F
H
M
B
连结AC
所以:EF∥MH,且 EF=MH
所以:四边形EFHM是平行四边形.
解:
A
B
C
D
E
F
H
M
因为EF是△ABC的一条中位线,所以EF∥AC,且EF= AC
因为:MH 是△DAC 的一条中位线,
所以:MH∥AC,且 MH= AC
本节课你学到什么?
三角形的中位线平行于第三边,并且等于它的一半
连接三角形两边中点的线段叫做三角形的中位线
⑵已知:△ABC三边长分别为a,b,c,它的三条中位线组成△DEF,△DEF的三条中位线又组成△HPN,则△HPN的周长等于——————,为△ABC周长的——, 面积为△ABC面积的——,
⑴已知:三角形的各边分别为6cm,8cm, 10cm,则连结各边中点所成三角形的周长为——cm,面积为——cm2,为原三角形面积的——。
6
10
8
3
5
4
B
C
A
D
E
F
∠B —— ∠ADE(填“=”或“≠”)
=
H
P
N
⑷如图,AF=FD=DB,FG∥DE∥BC,PE=1.5,则DP= ———,BC= ———
3
4.5
9
1.5
P
A
B
F
G
E
C
D
如图,△ABC的边BC,CA,AB 的中点分别是D,E,F.
(1)四边形AFDE 是平行四边形吗 为什么
(2)四边形AFDE 的周长
等于AB+AC 吗
为什么
B
C
D
F
E
A
