第10章 数据离散程度的度量

§10.1 数据的离散程度
教师寄语：精神成就事业，态度决定一切。
学习目标：
1、通过实例，知道描述一组数据的分布时，除关心它的集中趋势外，还需分析数据的波动大小。
2、知道数据离散程度的意义。
学习重难点：
对数据的离散程度的意义的理解。
学习难点：
对数据的收集、整理、描述和分析
学习过程：
一、快乐预习：
明确任务：预习课本P92—P93，完成下列题目。
1.甲、乙两名运动员的训练成绩的平均数 ，众数 中位数
2.观察图10-1，你发现那名运动员的成绩波动范围较大？谁的成绩比较稳定？
3.对于一组数据，仅仅了解数据的 是不够的，还需要了解这些数据的 和
的差异程度。
4.在实际生活中，我们除了关心数据的集中趋势（即 ）外，还要关注数据的 ，即一组数据的 。
预习检测：
①阅读课本P92交流与发现，完成P93练习第1题。
二、合作探究
1、甲、乙两支仪仗队队员的身高（cm）如下：
甲队：178、177、179、179、178、178、177、178、177、179
乙队：178、177、179、176、178、180、180、178、176、178
a、甲、乙两队队员的平均身高分别是多少？
b、作出折线统计图，你发现哪个队队员身高波动幅度较小？
2、完成课本p93页习题10.1A 组1、2题
三、拓展提高：
甲、乙两位同学参加奥赛班的11次测验成绩如下：
甲：90、93、93、90、98、100、95、100、99、100、98
乙：99、92、98、92、99、96、94、96、95、98、97
（1）它们的平均成绩分别是多少？
（2）它们测验成绩最高成绩与最低成绩分别相差多少？
（3）要从中选择一人参加奥赛，成绩达到98分以上才可以进入决赛，你认谁参赛合适，为什么？
（4）分析两位同学成绩各有何特点？并对两位同学各提一条建议。
四、感恩达标：（1、2题每空2分，3题每题2分）
1、一组数据的集中趋势的数据有 。
2、离散程度来描述一组数据的 和 。
3、甲、乙两班投篮比赛，每班各派10名同学，每人投10次，投中次数如下：
甲班：7、8、6、8、6、5、4、9、10、7
乙班：7、7、6、8、6、7、8、5、9、7
a、有人说这两个班投篮水平相当，为什么？
b、请依据数据制成折线统计图来说明结论。
§10.2 极 差
教师寄语：静下来，铸我实力；拼上去，亮我风采。
学习目标
1、知道极差的意义，会计算一组数据的极差。
2、能说出极差在反映数据离散程度的优缺点。
学习重难点
重点：极差的意义及计算。
难点：极差在反映数据的特点。
学习过程：
一、快乐预习：尝试独立完成下列问题．
1、预习课本P94—P95页，完成下列填空。
（1） 叫极差，
即：极差= 。
（2）极差反映一组数据的 ，用极差描述这组数据的离散程度 ，极差越大，数据的离散程度 。
（3）由于极差忽视了一组数据中所有数据之间的差异，仅仅由其中的最大值和最小值确定，个别远离群体的极端值在很大程度上影响 ，因而极差往往不能充分反映 。
2、自学课本例1，例2，；
二、合作探究：
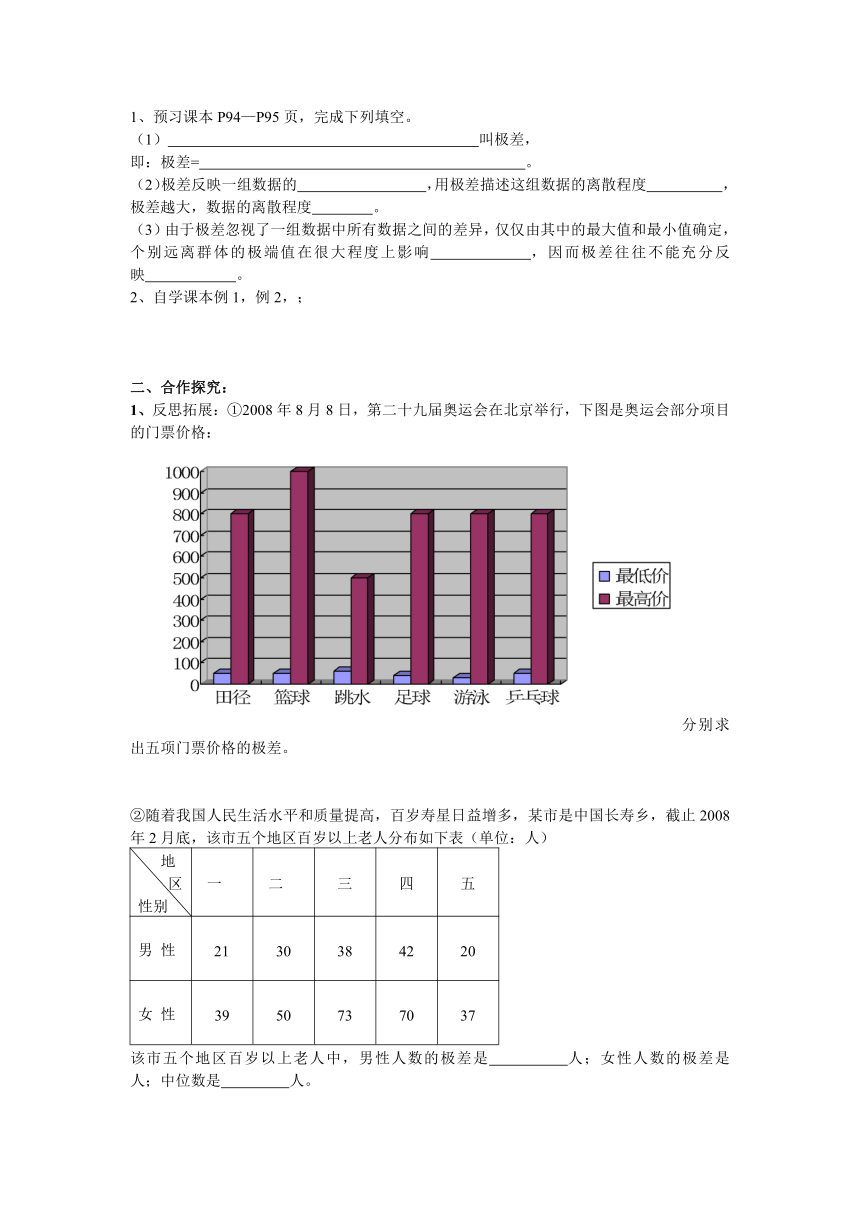
1、反思拓展：①2008年8月8日，第二十九届奥运会在北京举行，下图是奥运会部分项目的门票价格：
分别求出五项门票价格的极差。
②随着我国人民生活水平和质量提高，百岁寿星日益增多，某市是中国长寿乡，截止2008年2月底，该市五个地区百岁以上老人分布如下表（单位：人）
地区性别 一 二 三 四 五
男 性 21 30 38 42 20
女 性 39 50 73 70 37
该市五个地区百岁以上老人中，男性人数的极差是 人；女性人数的极差是 人；中位数是 人。
2、完成课后练习p96页1、2：
3、完成课后p96页习题10.2A组1、2
三、拓展提高：
《配套练习册》p41页5、6题
四、限时作业：（每题2分）
1、一组数据：473、865、368、774、539、474的极差是 ，一组数据1736、1350、-2114、-1736的极差是 .
2、一组数据3、-1、0、2、X的极差是5，且X为自然数，则X= .
3、下列几个常见统计量中能够反映一组数据波动范围的是（ ）
A.平均数 B.中位数 C.众数 D.极差
4、一组数据X1、X2…Xn的极差是8，则另一组数据2X1+1、2X2+1…，2Xn+1的极差是（ ） A. 8 B.16 C.9 D.17
5、试计算下列两组数据的极差：
A组：0, 10, 5, 5, 5, 5, 5, 5, 5, 5；
B组：4, 6, 3, 7, 2, 8, 1, 9, 5, 5。
§10.3 方差与标准差（第1课时）
教师寄语：拼一载春秋，搏一生无悔
学习目标：
1、会利用方差、标准差公式计算简单数据的方差和标准差。
2、能充分体会理解方差、标准差是刻画一组数据离散程度的两个重量的量。
学习重点、难点：
重点：方差、标准差公式及运算。
难点：方差、标准差能刻画一组数据的离散程度。
学习过程：
一、快乐预习：尝试独立完成下列问题．
阅读教材P98—P100内容，自主完成下列问题：
我们在数据处理时，首先关心能够反映一组数据集中趋势的量，这些量是 ，其次是关心这组数据的波动范围，这就是关注数据的离散程度，通常用 反映
1、除用极差这个量来反映这组数据的离散程度外，你还知道用什么来反映这组数据的离散程度？
2、 叫偏差，它可以反映一个数据偏离 的程度，但不能用偏差的和来反映一组数据的 。
3、 叫方差，方差的计算公式 。
4、 叫标准差，标准差的计算公式 。
二、合作探究：
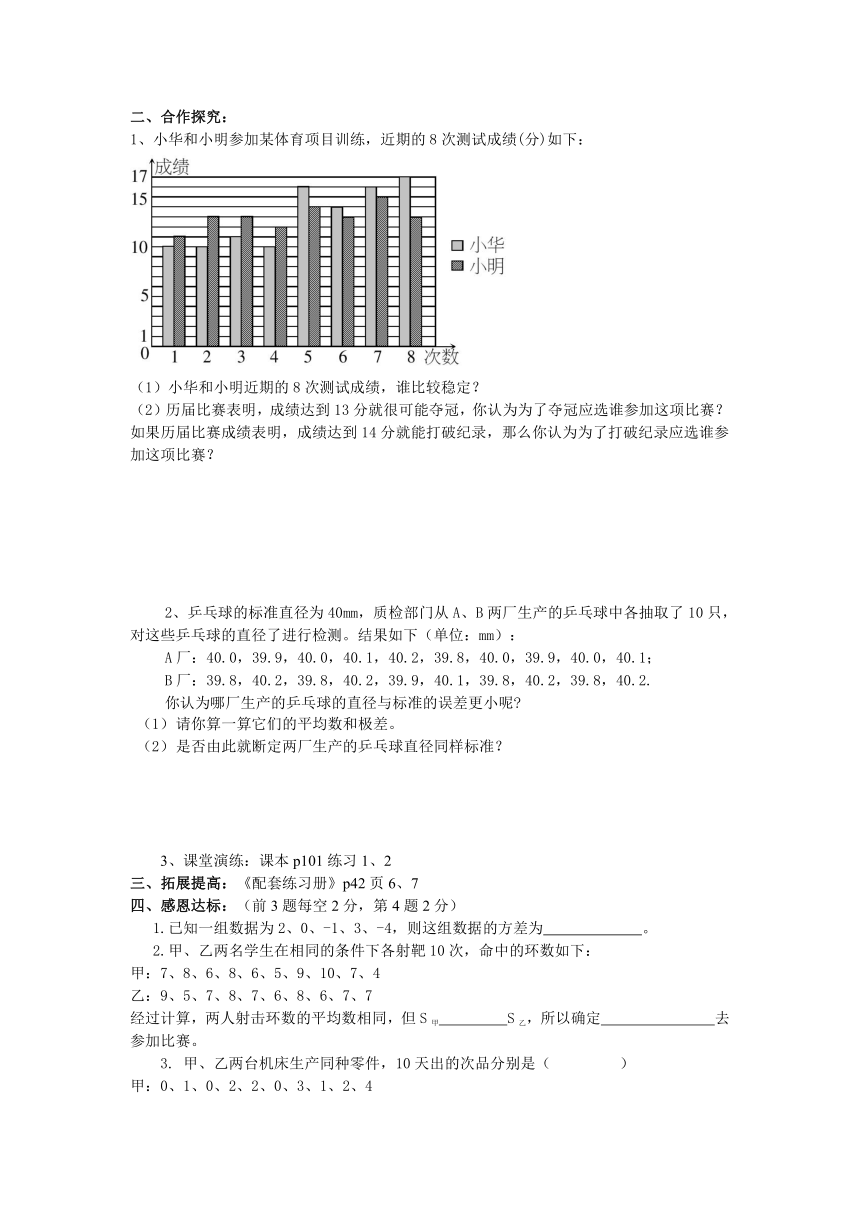
1、小华和小明参加某体育项目训练，近期的8次测试成绩(分)如下：
（1）小华和小明近期的8次测试成绩，谁比较稳定？
（2）历届比赛表明，成绩达到13分就很可能夺冠，你认为为了夺冠应选谁参加这项比赛？如果历届比赛成绩表明，成绩达到14分就能打破纪录，那么你认为为了打破纪录应选谁参加这项比赛？
2、乒乓球的标准直径为40mm，质检部门从A、B两厂生产的乒乓球中各抽取了10只，对这些乒乓球的直径了进行检测。结果如下（单位：mm）：
A厂：40.0，39.9，40.0，40.1，40.2，39.8，40.0，39.9，40.0，40.1；
B厂：39.8，40.2，39.8，40.2，39.9，40.1，39.8，40.2，39.8，40.2.
你认为哪厂生产的乒乓球的直径与标准的误差更小呢
请你算一算它们的平均数和极差。
是否由此就断定两厂生产的乒乓球直径同样标准？
3、课堂演练：课本p101练习1、2
三、拓展提高：《配套练习册》p42页6、7
四、感恩达标：（前3题每空2分，第4题2分）
1.已知一组数据为2、0、-1、3、-4，则这组数据的方差为 。
2.甲、乙两名学生在相同的条件下各射靶10次，命中的环数如下：
甲：7、8、6、8、6、5、9、10、7、4
乙：9、5、7、8、7、6、8、6、7、7
经过计算，两人射击环数的平均数相同，但S甲 S乙，所以确定 去参加比赛。
3. 甲、乙两台机床生产同种零件，10天出的次品分别是（ ）
甲：0、1、0、2、2、0、3、1、2、4
乙：2、3、1、2、0、2、1、1、2、1
分别计算出两个样本的平均数和方差，根据你的计算判断哪台机床的性能较好？
4．若1，2，3，a的平均数是3，又4，5，a，b的平均数是5，则0，1，2，3，4，a，b的方差是多少？
§10.3 方差与标准差（第2课时）
教师寄语：眼泪不是我们的答案，拼搏才是我们的选择。
学习目标：
1、知道可以用样本、方差、样本、标准差去推断总体与方差，总体与标准差。
2、能运用方差、标准差解释统计结果，并根据结果作出简单判断，从而帮助决策者作出恰当决策。
学习重点、难点：依据统计结果，作出恰当决策。
学习过程
一、快乐预习：
阅读课本，独立完成下列问题：
1、研究一组数据的离散程度一般用 等。其一般规律是 。
2、一组数据的离散程度，就是通常所指的这组数据的稳定性，离散程度越小，稳定性越高。因此研究数据的稳定性指标一般用 等。
3、样本方差的作用是（ ）
A、估计总体的平均水平 B、表示样本的平均水平
C、表示总体的波动大小
D、表示样本的波动大小，从而估计总体的波动大小
（2）一个样本的方差是0，若中位数是，那么它的平均数是（ ）
A、等于 B、不等于 C、大于 D、小于
4、已知样本数据101，98，102，100，99，则这个样本的标准差是（ ）
A、0 B、1 C、 D、2
5、如果给定数组中每一个数都减去同一非零常数，则数据的（ ）
A、平均数改变，方差不变 B、平均数改变，方差改变
C、平均数不变，方差不变 A、平均数不变，方差改变
二、合作探究：
1、解决课本101-102页的例2例3
2、一组数据为x1，x2，… …x10，另一组数据为x1—10，x2—10，… …x10—10，这两组的方差有何关系？
3、完成课后练习p103页1、2
三、拓展提高：
某校要从甲、乙两名跳高运动员中挑选一人参加一项校际比赛，在最近的8次选拔赛中，他们的成绩（单位：m）如下
甲：1.70，1.65，1.68，1.69，1.72，1.73，1.68，1.67
乙： 1.60，1.73，1.72，1.61，1.62，1.71，1.70，1.75
（1）他们的平均成绩分别是多少？
（2）哪个人的成绩更为稳定？
（3）经预测，跳高1.65m就很可能获得冠军，该校为了获取跳高比赛冠军，可能选哪位运动员参赛？若预测跳高1.70m方可获得冠军呢？
四、感恩达标：（每空2分）
（1）一组数据：，，0，，1的平均数是0，则= .方差 .
（2）如果样本方差，那么这个样本的平均数为 .样本容量为 .
（3）已知的平均数10，方差3，则的方差为 .
§10.4用科学计算器求方差和标准差
教师寄语：学而不思则惘，思而不学则殆
学习目标:
1、会用科学计算器求一组数据的平均数，方差和标准差。
2、养成耐心、细致的学习态度和实事求是的科学精神。
学习重难点：
重点：学会用计算器求标准差
难点：会用科学计算器求一组数据的平均数，方差和标准差。
学习过程：
一、快乐预习：
问题导读：
预习课本P105—P107页，完成下列填空。（要求必须熟悉计算器操作程序）
（1）按键__________，打开计算器。
（2）按键__________，__________ ，进入统计状态，计算器显示“SD”符号。
（3）按键__________，__________，_______ =，清除计算器中原有寄存的数据。
（4）输入统计数据，按键顺序为：第一数据__________ ；第二数据为__________，……最后一个数据 。
（5）按键__________，__________，_______ =，计算器显示出输入的所有统计数据的平均数。
（6）按键__________，__________，_______ =，计算器显示出输入的所有统计数据的标准差。
（7）按键__________=计算器显示出输入的所有统计数据的方差。
（8）若又准备保留数据，可按键______，______，_______结束求方差运算。
二、合作探究：
1、小组合作或独立完成例1
2、已知：甲、乙两组数据分别为：
甲：1，2，3，4，5，6，
乙：2，3，4，5，6，7，
计算这两组数据的方差
3、八（1)班在一次单元测验中的数学成绩如下：
83 74 81 50 87 92 75 94 87 92 83 77 74 70 80 91
78 66 92 89 93 89 87 86 78 89 75 86 78 49 86 75 92
79 90 75 72 99 80 76 88 84 79 80 82 84 85 99 83 90
82 88 70 90 79 88 63 73 91 63 68
请你计算出该班数学成绩的平均分、方差与标准差．
三、拓展提高：
甲、乙两台包装机同时分装质量为400g的奶粉，从它们各自分装的奶粉中随机抽取了10袋，测得它们的实际质量（单位:8）如下：
甲：401 400 408 406 410 409 400 393 394 394
乙：403 404 396 399 402 401 405 397 402 399
试问：哪台包装机包装的奶粉质量比较稳定？
三、感恩达标：（1、2、3题每题2分，4题4分）
1、一组数据2，3，2，3，5的方差是（ ）
A、6 B、3 C、1.2 D、2
2、甲、乙、丙、丁四人进行射击测试，每人射击成绩的平均数都是9.2环，方差分别为S2甲=0.56，S2乙=0.60，S2丙=0.50，S2丁=0.45，则成绩最稳定的是（ ）
A、甲 B、乙 C、丙 D、丁
3、有一组数据如下：3，a，4，6，7，它们的平均数是5，那么这组数据的方差是（ ）
A、10 B、√10 C、2 D、√2
4、甲组：76，90，84，86，81，87，86，82，88，85
乙组：82，84，85，89，79，91，80，89，74，79
回答：（1）甲组数据众数是_________，乙组数据中位数是____________ 。
（2）若甲组数据的平均数为X，乙组数据的平均数为 Y， 则X与Y的大小关系是_________________________ 。
（3）经计算可知：S2甲=14.45，S2乙=26.36，S2甲＜S2乙，这表明____________________________。（用简要文字语言表达）
第10章 数据离散程度的度量复习学案
教师寄语：最浪费不起的是时间
复习目标：
1、通过复习熟练掌握考察数据离散程度的量及意义。
2、能根据数据统计结果作出简单判定与决策。
学习过程：
一、本章知识结构：
极 差——概念
概 念—— 用科学
方 差—— 公 式—— 计算器
数据离散程度的度量 计算方
标准差—— 概 念—— 差和标
公 式—— 准差。
二、依据知识结构翻阅课本与笔记本记忆基本知识点
1、检查知识点
2、完成下列题目：
（1）样本2，3，0，5，-7，6的极差是 。
（2）下面几个概念中，能体现一组数据离散程度的是 。
A、平均数 B、中位数 C、众数 D、极差
（3）数学老师对小明参加的4次中考模拟的考试成绩进行统计分析，判断小明成绩是否稳定的应计算的数学量是 。
A、平均数 B、中位数 C、众数 D、方差
（4）已知1，2，3，4，5的方差为s2，则11,12，13，14，15这组数的方差是 。
3、专题研究：
（1）甲、乙两个小组各6名同学，某次数学测验成绩如下：
甲：76，90，84，86，81，81
乙：82，80，85，89，79，80
甲组的众数是 ，乙组的中位数是 ，甲组的方差是 ，乙组的方差是 ，由计算知学习成绩较稳定的小组是 。
（2）为了从甲、乙两名射击选手中选出一人参加射击比赛，辅导员对它们的实际水平进行了测试，每人射击10次，成绩如下：
甲：9，9，10，8，6，10，10，8，10，8
乙：10，8，7，10，10，10，10，8，7，8
你如何帮助辅导员作出决策？
三、感恩达标：（每小题2分）
1、下列说法正确的是（ ）
A、如果两名运动员的训练成绩的平均数、众数、中位数相同则他们的成绩一样B、一组数据的方差总是大于标准差
C、一组数据的方差越大，则这组数据的波动越小
D、一组数据的方差越小，则这组数据的波动越小
2、已知一组数据为-1，0，x，1，-2的平均数是0那么这组数据的方差是 。
3、一组数据x1，x2，… …xn的方差s2=0.36，则这组数据x1，x2，… …xn，x的方差是（ ）。
4、一个样本的方差s2=1/50【（x1- 5）2+（x2- 5）2+… …+（xn- 5）2】那么这个样本的容量是 ，平均数是 。
5、已知样本x1，x2，… …xn的方差为2，平均数是6，则3x1+2，3x2+2，… …3xn+2的方差是 ，平均数是 。
6、某校要从甲、乙两名跳远运动员中挑选一人参加一项校际比赛．在最近10次选拔赛中，他们的成绩（单位:cm）如下：
甲：585 596 610 598 612 597 604 600 597 601
乙：613 618 580 581 618 593 585 590 598 624
（1）他们的平均成绩分别是多少？
（2）甲、乙这10次比赛成绩的方差分别是多少？
　　第10章 数据的离散程度单元测试
一、选择题（每题3分，共30分）
1、数据2，3，3，5，7的极差为（ ）
A、2 B、3 C、4 D、5
2、在统计中，样本的标准差可以反映这组数据的（ ）
A、平均状态 B、分布规律 C、离散程度 D、数值大小
3、下列说法正确的是（ ）
A、方差反映的是一组数据的波动大小，方差的值一定是正数
B、已知一组数据的方差计算公式为s2=1/5（x12+x22+x32+x42+x52-20），则这组数据的平均数为2
C、数据1，2，2，3，3，4的众数是2
D、一组数据x1，x2，x3，… …xn，都减去a值的平均数为m，方差为n，则这组数据的平均数为a+m，方差为n
4、老师对小明本学期的5次数学测试成绩进行统计分析，判断小明的数学成绩是否稳定，老师需要知道小明这5次数学成绩的（ ）
A、平均数 B、方差 C、众数 D、频数
5、样本方差的作用是 （ ）
A、样本数据的多少 B、样本数据的平均水平
C、样本数据在各个范围中所占比例大小 D、样本数据的波动程度
6、已知样本：1，2，-3，-2，3，0，-1，那么样本数据的标准差为（ ）
A、0 B、√2 C、2 D、4
7、甲、乙、丙三名射击运动员在某场测试中各射击20次，3人的测试成绩如下表：
甲的成绩
环数 7 8 9 10
频数 4 6 6 4
乙的成绩
环数 7 8 9 10
频数 6 4 4 6
丙的成绩
环数 7 8 9 10
频数 5 5 5 5
甲、乙、丙三名运动员测试成绩最稳定的是（ ）
A、甲 B、乙 C、丙D、3人成绩稳定情况相同
8、为了判断甲、乙两个小组的学生英语测试成绩哪一组比较整齐，通常要知道两组成绩的（ ）
A、平均数 B、众数 C、方差 D、中位数
9、若一组数据1，2，3，x的极差是6，则x的值是（ ）
A、7 B、8 C、9 D、7或-3
10、一组数据1，2，3，4，5的方差是
A、1 B、2 C、3 D、4
二、填空。（每题3分，共24分）
1、样本-2，-1，0，3，5的平均数是 ，极差是 ，方差是 ，标准差是 。
2、某体委准备从甲、乙两名射击运动员中选拔1人参加全运会，每人各打靶5次，打中环数分别如下，甲：7，8，9，8，8；乙：5，10，6，9，10，那么应该选 运动员参加全运会。
3、一组数据35，35，36，36，37，38，38，38，39，40的极差是 。
4、5名同学目测同一本教科书的宽度时，产生的误差如下（单位：cm）：2，-2，-1，1，0，则这组数据的极差为 cm。
5、某学校篮球队五名队员的年龄分别为17，15，17，16，15，其方差为0.8，则三年后这五名运动员年龄的方差为 。
6、已知一组数据1，2，0，-1，x，1的平均数是1，则这组数据的极差为 。
7、一组数据2,6，x，10，8的平均数是6，则这组数据的方差是 。
8、甲、乙、丙三台包装机同时分装质量为400g的茶叶，从它们各自分装的茶叶中分别随机抽取了10盒，得到它们的实际质量的方差如下表所示，根据表中的数据，可以认为三台包装机中， 包装机包装的茶叶质量最稳定。
甲包装机 乙包装机 丙包装机
方差 31.96 7.96 16.32
三、解答题。（10+12+10+12，共46分）
1、某农场种植甲、乙两种水稻，在连续6年中各年的平均亩产量如下（单位：千克）
品 种 第1年 第2年 第3年 第4年 第5年 第6年
甲 450 460 450 425 455 460
乙 445 480 475 425 430 445
哪种水稻在6年中的产量比较稳定？
2、小明和小兵参加体育项目训练，近期的8次测试成绩（单位：分）如下表：
测试 第1次 第2次 第3次 第4次 第5次 第6次 第7次 第8次
小明 10 10 11 10 16 14 16 17
小兵 11 13 13 12 14 13 15 13
（1）根据上表提供的数据填写下表：
平均数 众 数 中位数 方 差
小 明 10 8.25
小 兵 13 13
（2）若从中选一人参加中学生运动会，你认为选谁合适呢？请说明理由。
3、已知数据6，7，10，13，14，的方差为10，你不用计算。
（1）你能说出数据306，307，310，313，314的方差吗？
（2）能说出数据12，14，20，26，28的方差吗？
4、小明和小华假期到工厂体验生活，加工直径为100mm的零件，为了检验他们加工的产品质量，从中各抽出6件进行测量，测得数据如下（单位：mm）：
小明：99，100，98，100，100，103
小华：99，100，102，99，100，100
（1）分别计算小明和小华这6件产品的极差、平均数和方差
（2）根据你的计算结果，说明他们俩人水加工的零件更符合要求。
第10章 数据离散程度的度量练习题
一、选择题
1．数据5，7，7，8，10，11的标准差是（ ）
A．8 B．4 C．2 D．1
2．已知甲、乙两组数据的平均数相等，若甲组数据的方差S2甲＝0.055，乙组数据的方差 S2乙＝0.105，则（ ）
A．甲组数据比乙组数据波动大
B．乙组数据比甲组数据波动大
C．甲组数据与乙组数据的波动一样大
D．甲、乙两组数据的数据波动不能比较
3．数据2，3，3，5，7的极差是（ ）
A．2 B．3 C．4 D．5
4．在统计中，样本的方差可以近似地反映总体的（ ）
A．平均状态 B．波动大小
C．分布规律 D．最大值和最小值
5．一组数据1，3，2，5，x的平均数为3，则数据的方差为（ ）
A．10 B．2 C． 3 D．4
6．小明通过计算甲、乙、丙、丁四组数据的方差后，发现有三组数据的方差相同，请你通过观察或计算，找出方差不同的一组数据（ ）
A．102 103 105 107 108 B．2 3 5 7 8
C．4 9 25 49 64 D．1102 1103 1105 1107 1108
7．如果数据x1，x2，x3，…，x8的方差等于a，那么新数据6x1+3，6x2+3，6x3+3，…，6x8+3的方差为（ ）
A．6a+3 B．6a C．36a D．36a+3
7.计算一组数据：8，9，10，11，12的方差为（ ）
A．1 B．2 C．3 D．4
8.甲、乙二人在相同情况下，各射靶10次，两人命中环数的平均数都是7，方差S甲2＝3，S乙2＝1.2，则射击成绩较稳定的是（ ）
A．甲 B．乙 C．一样 D．不能确定
9.甲、乙两八年级学生在一学期里多次检测中，其数学成绩的平均分相等，但他们成绩的方差不等，那么正确评价他们的数学学习情况的是（ ）
A．学一样
B．成绩虽然一样，但方差大的学生学习潜力大
C．虽然平均成绩一样，但方差小的学习成绩稳定
D．方差较小的学习成绩不稳定，忽高忽低
二、填空题
1、检查5个篮球的质量，把超过标准质量的克数记为正数，不足标准质量的克数记为负数，检查结果如下表，则最接近标准质量的是 号篮球，最偏离标准质量的是 号篮球，这次测量结果的极差是 ．
篮球编号 1 2 3 4 5
与标准质量差（g） +4 +7 -3 -8 +9
2．甲、乙、丙三台机床生产直径为60mm的螺丝，为了检验产品质量，从三台机床生产的螺丝中各抽查了20个测量其直径，进行数据处理后，发现这三组数据的平均数都是60mm，它们的方差依次为s2甲=0.162，s2乙=0.058，s2丙=0.149．根据以上提供的信息，你认为生产螺丝质量最好的是 机床．
3．某超市出售的三种品牌的面粉袋上，分别标有质量为（25±0.1）kg、（25±0.2）kg、（25±0.3）kg的字样，从中随意抽取两袋，它们的质量最多相差 kg．
4．小明五次测试成绩为:91、89、88、90、92，则这五次测试成绩的平均数是 ，方差是 ．
5．若数据11，12，12，20，11，x的众数是12，则这组数据的方差是 ．
6．已知数据x1，x2的方差是s2，则数据x1+b，x2+b的方差是 ．
7.一组数据5，8，x，10，4的平均数是2x，则这组数据的方差是________．
8.2.5名同学目测同一本教科书的宽度时，产生的误差如下（单位：cm）：
2，－2，－1，1，0，则这组数据的极差为______cm．
9.若样本1，2，3，x的平均数为5，又样本1，2，3，x，y的平均数为6，
则样本1，2，3，x，y的极差是_______，方差是_______，标准差是______．
10.已知一组数据0，1，2，3，4的方差为2，则数据20，21，22，23，24的方差为_____， 标准差为________．
11.一组数据－8，－4，5，6，7，7，8，9的极差是______，方差是_____，标准差是______．
12.若样本x1，x2，……，xn的平均数为 ＝5，方差S2＝0.025，则样本4x1，4x2，……，4xn的平均数是_____，方差_______．
三、解答题
1．甲、乙两位同学五次数学测验成绩如下表：
测验(次) 1 2 3 4 5 平均数 方差
甲(分) 75 90 96 83 81
乙(分) 86 70 90 95 84
请你在表中的空白处填上适当的数，用学到的统计知识对两位同学的成绩进行分析，并写出一条合理化建议．

2．某校八年级(1)班、(2)班各有49名学生，两班在一次数学测验中的成绩统计如下表：
班级 平均分 众数 中位数 标准差
八年级(1)班 79 70 87 19.8
八年级(2)班 79 70 79 5.2
(1)请你对下面的一段话予以简要分析：
八年级(1)班的小刚回家对妈妈说：“昨天的数学测验，全班平均79分，得70分的人最多，我得了85分，在班里可算上游了!”
(2)请你根据表中数据，对这两个班的测验情况进行简要分析，并提出教学建议．

3．若1，2，3，a的平均数是3，又4，5，a，b的平均数是5，则0，1，2，3，4，a，b的方差是多少？

4．某校要从甲、乙两名跳远运动员中挑选一人参加一项校际比赛．在最近10次选拔赛中，他们的成绩（单位:cm）如下：
甲：585 596 610 598 612 597 604 600 597 601
乙：613 618 580 581 618 593 585 590 598 624
（1）他们的平均成绩分别是多少？
（2）甲、乙这10次比赛成绩的方差分别是多少？
5某县种鸡场为研究不同种鸡的产蛋量，各选十只产蛋母鸡，它们十天的产蛋量如下表，试问这两种鸡哪个产蛋量比较稳定？
6.12 6.13 6.14 6.15 6.16 6.17 6.18 6.19 6.20 6.21
甲 9 9 7 9 8 9 9 10 9 7
乙 9 8 10 7 8 8 9 8 8 8




6.在某旅游景区上山的一条小路上，有一些断断续续的台阶，如图是其中的甲、乙段台阶路的示意图．
请你用所学过的有关统计知识（平均数，中位数，方差和极差）回答下列问题：
（1）两段台阶路有哪些相同点和不同点？
（2）哪段台阶路走起来更舒服？为什么？
（3）为方便游客行走，需要重新整修上山的小路，对于这两段台阶路，在台阶数不变的情况下，请你提出合理的整修建议．
下图中的数字表示第一级台阶的高度（单位：cm），并且数15，16，16，14，14，15的方差S甲2＝ ，数据11，15，18，17，10，19的方差S乙2＝






7.甲、乙两班举行电脑汉字输入速度比赛，各选10名学生参加，各班参赛学生每分钟输入汉字个数统计如下表：
输入汉字（个） 132 133 134 135 136 137 众数 中位数 平均数（x） 方差（S2）
甲班学生（人） 1 0 1 5 2 1 135 135 135 1.6
乙班学生（人） 0 1 4 1 2 2
请填写上表中乙班学生的相关数据，再根据所学的统计学知识，从不同方面评价甲、乙两班学生的比赛成绩．（至少从两个方面进行评价）