2020-2021学年七年级数学下册北师大版第三章第3节《用图像表示的变量间关系》同步练习(word有答案)
文档属性
| 名称 | 2020-2021学年七年级数学下册北师大版第三章第3节《用图像表示的变量间关系》同步练习(word有答案) |
|
|
| 格式 | zip | ||
| 文件大小 | 307.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-04-20 07:12:57 | ||
图片预览

文档简介
3 用图象表示的变量间关系
一、选择题
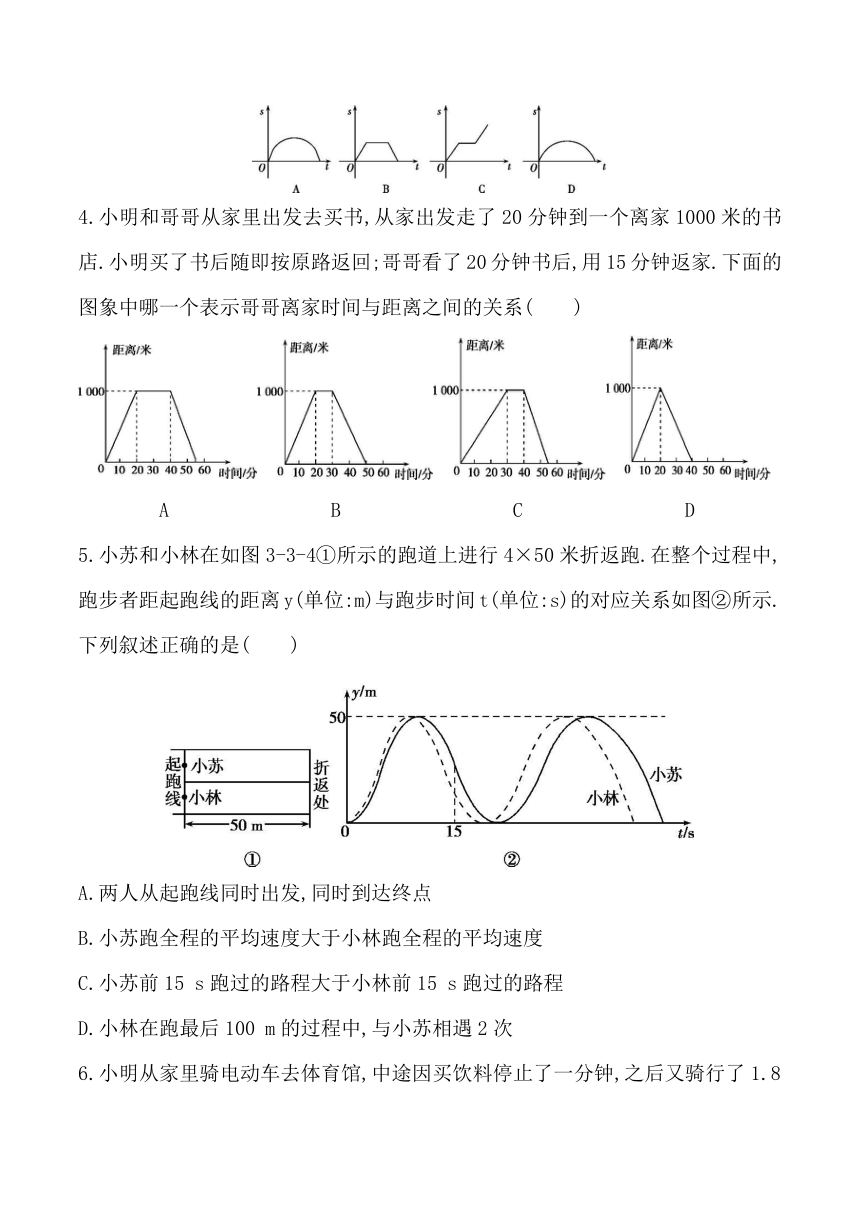
1.如图所示的容器内装满水,打开排水管,容器内的水匀速流出,则容器内液面的高度h随时间x变化的图象最接近实际情况的是( )
2.如图是一台自动测温仪记录的图象,它反映了我市冬季某天气温T随着时间t变化而变化的关系,观察图象得到下列信息,其中错误的是( )
A.凌晨4时气温最低,为-3
℃
B.14时气温最高,为8
℃
C.从0时至14时,气温随时间增长而上升
D.从14时至24时,气温随时间增长而下降
3.如图,一只蚂蚁从O点出发,沿着扇形OAB的边缘匀速爬行一周,当蚂蚁运动的时间为t时,蚂蚁与O点的距离为s,则s与t之间的关系图象大致是( )
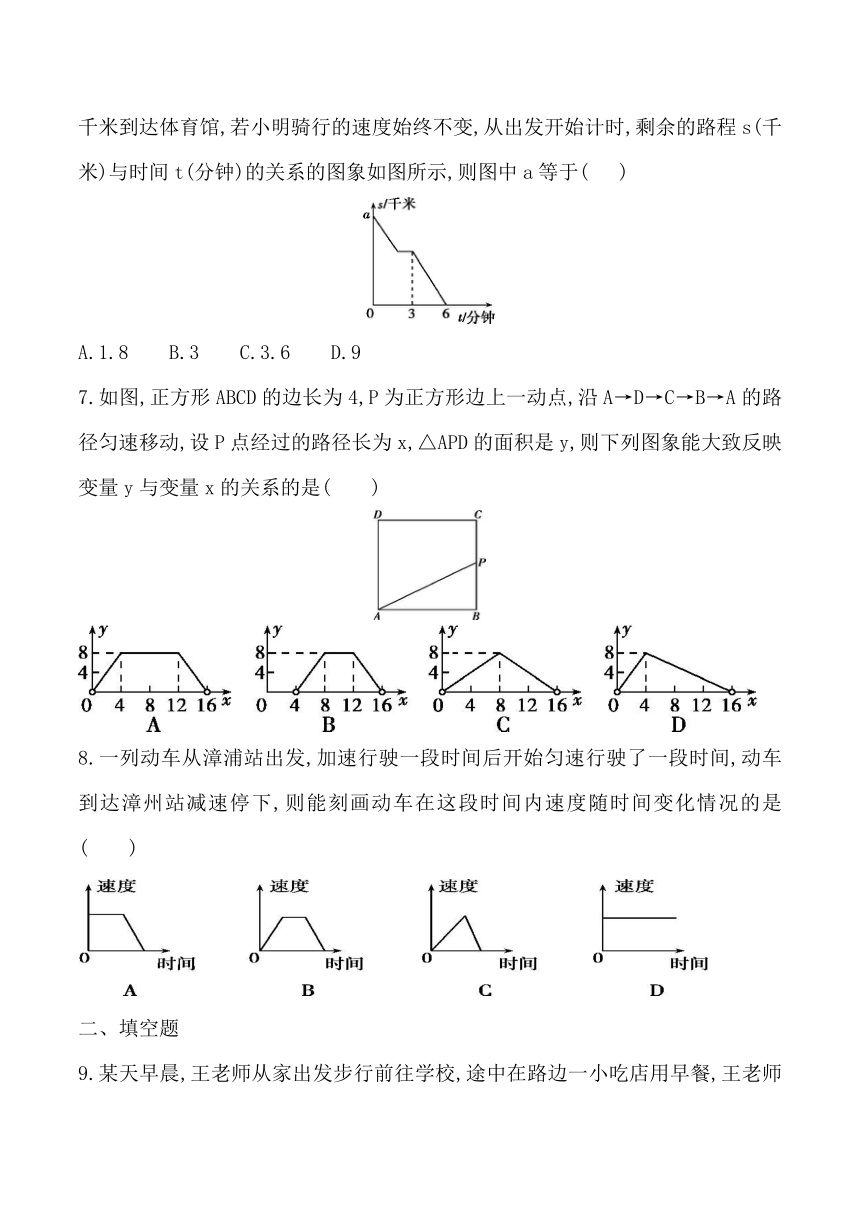
4.小明和哥哥从家里出发去买书,从家出发走了20分钟到一个离家1000米的书店.小明买了书后随即按原路返回;哥哥看了20分钟书后,用15分钟返家.下面的图象中哪一个表示哥哥离家时间与距离之间的关系(
)
A
B
C
D
5.小苏和小林在如图3-3-4①所示的跑道上进行4×50米折返跑.在整个过程中,跑步者距起跑线的距离y(单位:m)与跑步时间t(单位:s)的对应关系如图②所示.下列叙述正确的是( )
A.两人从起跑线同时出发,同时到达终点
B.小苏跑全程的平均速度大于小林跑全程的平均速度
C.小苏前15
s跑过的路程大于小林前15
s跑过的路程
D.小林在跑最后100
m的过程中,与小苏相遇2次
6.小明从家里骑电动车去体育馆,中途因买饮料停止了一分钟,之后又骑行了1.8千米到达体育馆,若小明骑行的速度始终不变,从出发开始计时,剩余的路程s(千米)与时间t(分钟)的关系的图象如图所示,则图中a等于(
)
A.1.8 B.3
C.3.6 D.9
7.如图,正方形ABCD的边长为4,P为正方形边上一动点,沿A→D→C→B→A的路径匀速移动,设P点经过的路径长为x,△APD的面积是y,则下列图象能大致反映变量y与变量x的关系的是( )
8.一列动车从漳浦站出发,加速行驶一段时间后开始匀速行驶了一段时间,动车到达漳州站减速停下,则能刻画动车在这段时间内速度随时间变化情况的是( )
二、填空题
9.某天早晨,王老师从家出发步行前往学校,途中在路边一小吃店用早餐,王老师从家到学校这一过程中的所走路程s(米)与时间t(分)之间的关系如图所示.
(1)他家与学校的距离为 米,从家出发到学校,王老师共用了 分钟;?
(2)王老师从家出发 分钟后开始用早餐,用早餐花了 分钟;?
(3)王老师用早餐前步行的速度是 米/分,用完早餐以后的速度是 米/分.?
10.火车匀速通过隧道时,火车在隧道内的长度y(米)与火车行驶时间x(秒)之间的关系用图象描述如图所示,有下列结论:
①火车的长度为120米;
②火车的速度为30米/秒;
③火车整体都在隧道内的时间为25秒;
④隧道长度为750米.
其中正确的结论是 (把你认为正确结论的序号都填上).?
11.某农场租用播种机播种小麦,在甲播种机播种2天后,又调来乙播种机参
与播种,直至完成800亩的播种任务,播种亩数与天数之间的关系如图所示,
那么乙播种机参与播种的天数是 ????天.
12.甲、乙两人在一条笔直的道路上相向而行,甲骑自行车从A地到B地,乙驾车从B地到A地,他们分别以不同的速度匀速行驶,已知甲先出发6分钟后,乙才出发,在整个过程中,甲、乙两人的距离y(千米)与甲出发的时间x(分)之间的关系如图所示,当乙到达终点A时,甲还需 ????分钟到达终点B.
三、解答题
13.某学校进行往返跑比赛,张佳同学去时以每秒
6
m的速度跑完,回来时以每秒5
m的速度跑回起点,时间与速度的变化如图所示.
(1)张佳共跑了多长时间?
(2)哪些时段保持匀速?速度分别是多少?
(3)试写出她在跑步过程中,离起点距离s(m)与时间t(s)之间的关系式.
14.高铁的开通,给衢州市民出行带来了极大的方便,“五一”期间,乐乐和颖颖相约到杭州市的某游乐园游玩,乐乐乘私家车从衢州出发1小时后,颖颖乘坐高铁从衢州出发,先到杭州火车东站,然后转乘出租车去游乐园(换车时间忽略不计),两人恰好同时到达游乐园,他们离开衢州的距离y(千米)与乘车时间t(小时)的关系如图所示.
请结合图象解决下面问题:
(1)高铁的平均速度是每小时 千米;
?
(2)私家车的平均速度为每小时多少千米?
(3)颖颖乘坐多少分钟出租车?
(4)若乐乐要提前18分钟到达游乐园,问私家车的速度必须达到多少千米/时?
15.甲骑自行车,乙骑摩托车,从A城出发到B城旅行,甲、乙两人离开A城所走的路程与时间之间关系的图象如图3-3-6所示,根据图象,解答:
(1)求甲在DE段的速度和乙的平均速度;
(2)乙出发多长时间与甲相遇?
答案
1.A
2.C
3.B
4.A
5.D
6.B
7.B
8.B
9. (1)1
000;25 (2)10;10 (3)50;100
(3)v早餐前==50米/分;v早餐后==100米/分.
10. 180
11.
4
12.
78
13. (1)因为陈灿全家10时到达旅游景点,当天14时离开景点返家,所以陈灿全家在景点游玩了4个小时.
(2)14时到15时,行驶了180-120=60(千米),故返程途中速度为60千米/小时.
14. 答案不唯一,如:(1)骑自行车者3小时后休息了1小时.
(2)骑自行车者的平均速度为=(km/h).如果不算休息的1小时,他骑车的平均速度为16
km/h.
(3)骑摩托车者的速度为40
km/h.
(4)骑摩托车者比骑自行车者晚出发3小时,早到1小时.
(5)骑摩托车者与骑自行车者在距出发点60千米处相遇.
15.(1)甲在DE段的速度为(100-60)÷(8-5)=(千米/小时),
乙的平均速度为100÷(6-4)=50(千米/小时).
(2)设乙出发t小时后与甲相遇,
由题意得50t=60+(t-1),
解得t=.
答:乙出发小时后与甲相遇.
一、选择题
1.如图所示的容器内装满水,打开排水管,容器内的水匀速流出,则容器内液面的高度h随时间x变化的图象最接近实际情况的是( )
2.如图是一台自动测温仪记录的图象,它反映了我市冬季某天气温T随着时间t变化而变化的关系,观察图象得到下列信息,其中错误的是( )
A.凌晨4时气温最低,为-3
℃
B.14时气温最高,为8
℃
C.从0时至14时,气温随时间增长而上升
D.从14时至24时,气温随时间增长而下降
3.如图,一只蚂蚁从O点出发,沿着扇形OAB的边缘匀速爬行一周,当蚂蚁运动的时间为t时,蚂蚁与O点的距离为s,则s与t之间的关系图象大致是( )
4.小明和哥哥从家里出发去买书,从家出发走了20分钟到一个离家1000米的书店.小明买了书后随即按原路返回;哥哥看了20分钟书后,用15分钟返家.下面的图象中哪一个表示哥哥离家时间与距离之间的关系(
)
A
B
C
D
5.小苏和小林在如图3-3-4①所示的跑道上进行4×50米折返跑.在整个过程中,跑步者距起跑线的距离y(单位:m)与跑步时间t(单位:s)的对应关系如图②所示.下列叙述正确的是( )
A.两人从起跑线同时出发,同时到达终点
B.小苏跑全程的平均速度大于小林跑全程的平均速度
C.小苏前15
s跑过的路程大于小林前15
s跑过的路程
D.小林在跑最后100
m的过程中,与小苏相遇2次
6.小明从家里骑电动车去体育馆,中途因买饮料停止了一分钟,之后又骑行了1.8千米到达体育馆,若小明骑行的速度始终不变,从出发开始计时,剩余的路程s(千米)与时间t(分钟)的关系的图象如图所示,则图中a等于(
)
A.1.8 B.3
C.3.6 D.9
7.如图,正方形ABCD的边长为4,P为正方形边上一动点,沿A→D→C→B→A的路径匀速移动,设P点经过的路径长为x,△APD的面积是y,则下列图象能大致反映变量y与变量x的关系的是( )
8.一列动车从漳浦站出发,加速行驶一段时间后开始匀速行驶了一段时间,动车到达漳州站减速停下,则能刻画动车在这段时间内速度随时间变化情况的是( )
二、填空题
9.某天早晨,王老师从家出发步行前往学校,途中在路边一小吃店用早餐,王老师从家到学校这一过程中的所走路程s(米)与时间t(分)之间的关系如图所示.
(1)他家与学校的距离为 米,从家出发到学校,王老师共用了 分钟;?
(2)王老师从家出发 分钟后开始用早餐,用早餐花了 分钟;?
(3)王老师用早餐前步行的速度是 米/分,用完早餐以后的速度是 米/分.?
10.火车匀速通过隧道时,火车在隧道内的长度y(米)与火车行驶时间x(秒)之间的关系用图象描述如图所示,有下列结论:
①火车的长度为120米;
②火车的速度为30米/秒;
③火车整体都在隧道内的时间为25秒;
④隧道长度为750米.
其中正确的结论是 (把你认为正确结论的序号都填上).?
11.某农场租用播种机播种小麦,在甲播种机播种2天后,又调来乙播种机参
与播种,直至完成800亩的播种任务,播种亩数与天数之间的关系如图所示,
那么乙播种机参与播种的天数是 ????天.
12.甲、乙两人在一条笔直的道路上相向而行,甲骑自行车从A地到B地,乙驾车从B地到A地,他们分别以不同的速度匀速行驶,已知甲先出发6分钟后,乙才出发,在整个过程中,甲、乙两人的距离y(千米)与甲出发的时间x(分)之间的关系如图所示,当乙到达终点A时,甲还需 ????分钟到达终点B.
三、解答题
13.某学校进行往返跑比赛,张佳同学去时以每秒
6
m的速度跑完,回来时以每秒5
m的速度跑回起点,时间与速度的变化如图所示.
(1)张佳共跑了多长时间?
(2)哪些时段保持匀速?速度分别是多少?
(3)试写出她在跑步过程中,离起点距离s(m)与时间t(s)之间的关系式.
14.高铁的开通,给衢州市民出行带来了极大的方便,“五一”期间,乐乐和颖颖相约到杭州市的某游乐园游玩,乐乐乘私家车从衢州出发1小时后,颖颖乘坐高铁从衢州出发,先到杭州火车东站,然后转乘出租车去游乐园(换车时间忽略不计),两人恰好同时到达游乐园,他们离开衢州的距离y(千米)与乘车时间t(小时)的关系如图所示.
请结合图象解决下面问题:
(1)高铁的平均速度是每小时 千米;
?
(2)私家车的平均速度为每小时多少千米?
(3)颖颖乘坐多少分钟出租车?
(4)若乐乐要提前18分钟到达游乐园,问私家车的速度必须达到多少千米/时?
15.甲骑自行车,乙骑摩托车,从A城出发到B城旅行,甲、乙两人离开A城所走的路程与时间之间关系的图象如图3-3-6所示,根据图象,解答:
(1)求甲在DE段的速度和乙的平均速度;
(2)乙出发多长时间与甲相遇?
答案
1.A
2.C
3.B
4.A
5.D
6.B
7.B
8.B
9. (1)1
000;25 (2)10;10 (3)50;100
(3)v早餐前==50米/分;v早餐后==100米/分.
10. 180
11.
4
12.
78
13. (1)因为陈灿全家10时到达旅游景点,当天14时离开景点返家,所以陈灿全家在景点游玩了4个小时.
(2)14时到15时,行驶了180-120=60(千米),故返程途中速度为60千米/小时.
14. 答案不唯一,如:(1)骑自行车者3小时后休息了1小时.
(2)骑自行车者的平均速度为=(km/h).如果不算休息的1小时,他骑车的平均速度为16
km/h.
(3)骑摩托车者的速度为40
km/h.
(4)骑摩托车者比骑自行车者晚出发3小时,早到1小时.
(5)骑摩托车者与骑自行车者在距出发点60千米处相遇.
15.(1)甲在DE段的速度为(100-60)÷(8-5)=(千米/小时),
乙的平均速度为100÷(6-4)=50(千米/小时).
(2)设乙出发t小时后与甲相遇,
由题意得50t=60+(t-1),
解得t=.
答:乙出发小时后与甲相遇.
同课章节目录
- 第一章 整式的乘除
- 1 同底数幂的乘法
- 2 幂的乘方与积的乘方
- 3 同底数幂的除法
- 4 整式的乘法
- 5 平方差公式
- 6 完全平方公式
- 7 整式的除法
- 第二章 相交线与平行线
- 1 两条直线的位置关系
- 2 探索直线平行的条件
- 3 平行线的性质
- 4 用尺规作角
- 第三章 变量之间的关系
- 1 用表格表示的变量间关系
- 2 用关系式表示的变量间关系
- 3 用图象表示的变量间关系
- 第四章 三角形
- 1 认识三角形
- 2 图形的全等
- 3 探索三角形全等的条件
- 4 用尺规作三角形
- 5 利用三角形全等测距离
- 第五章 生活中的轴对称
- 1 轴对称现象
- 2 探索轴对称的性质
- 3 简单的轴对称图形
- 4 利用轴对称进行设计
- 第六章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
