2020--2021学年人教版八年级下册数学19.2.4:一次函数的面积问题(共48张ppt)
文档属性
| 名称 | 2020--2021学年人教版八年级下册数学19.2.4:一次函数的面积问题(共48张ppt) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-04-20 00:00:00 | ||
图片预览







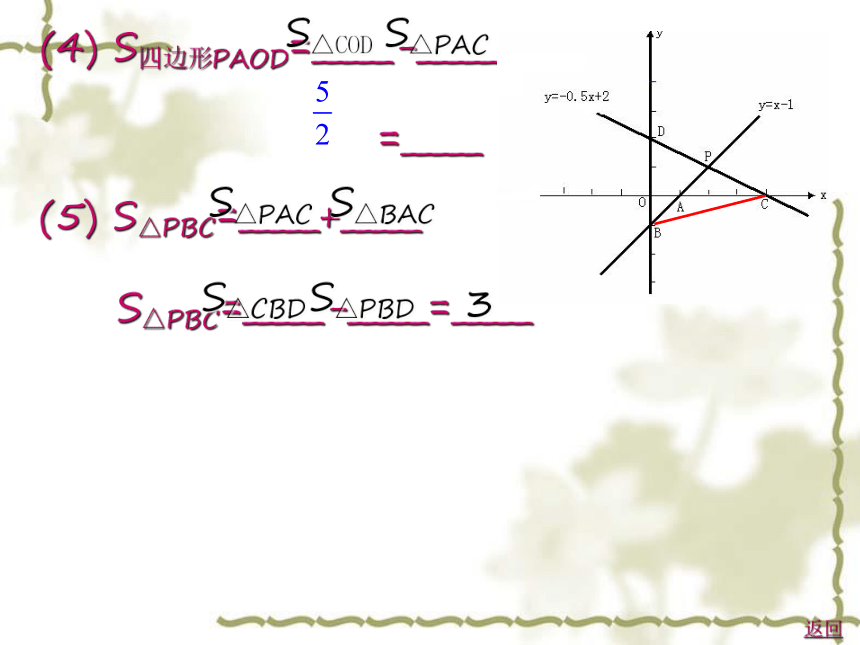
文档简介
(共48张PPT)
一次函数的面积问题
第十九章
一次函数
复习与回顾
2、求直线
与两坐标轴所围成的
三角形的面积.
1、已知一次函数
的图像平行
于直线
,且过点(-1,5),
求一次函数的
解析式.
3、将直线
平移,使其经过(4,3)
(1)求平移后的函数解析式
(2)求平移后的函数图像与两坐标轴围成的三角形面积
6
1.
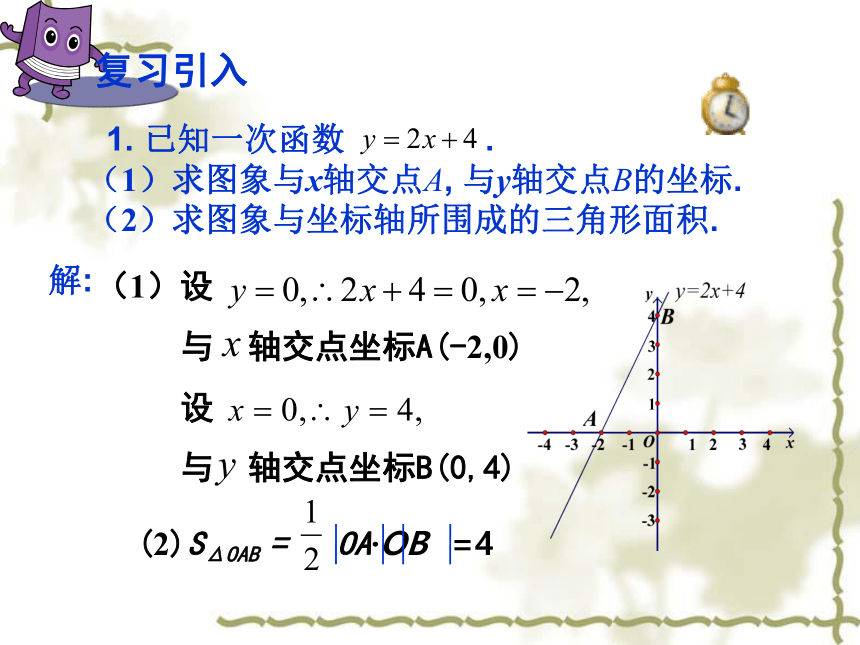
已知一次函数
.
(1)求图象与x轴交点A,
与y轴交点B的坐标.
(2)求图象与坐标轴所围成的三角形面积.
解:
(2)SΔOAB
=
OA·OB
=4
(1)设
与
轴交点坐标A(-2,0)
设
与
轴交点坐标B(0,4)
复习引入
2、求直线y=-1.5x+3与x轴、y轴所围成的三角形的面积。
y
x
O
A
B
3
2
解:当x=0时,y=3;
当y=0时,x=2;
∴A(0,3) B(2,0)
∴OA=3,OB=2
因此三角形的面积为3.
∴S△ABC= OA·OB
=
×3×2=3
求直线y=kx+b与x轴、y轴所围成的三角形的面积。
y
x
O
A
B
b
∴S△ABC=
知识探究
解:当x=0时,y=b;
当y=0时,x=
;
∴A(0,b), B(
,0)
∴OA=|b|,OB=
=
×
OA·OB
×|b|×
=
=
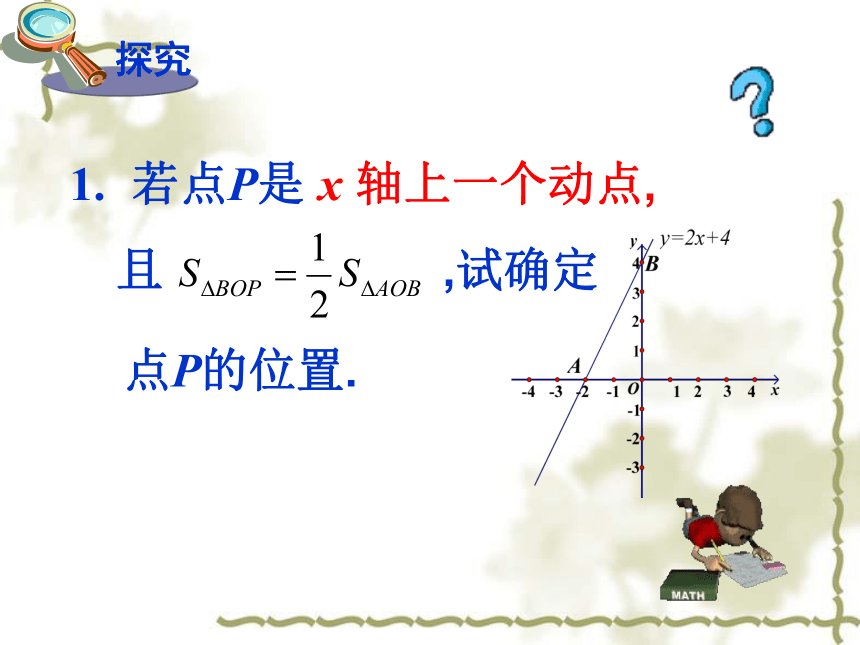
1.
若点P是
x
轴上一个动点,
且
,试确定
点P的位置.
探究
(1)若点P是y轴上一动点,
试确定点P的位置.
(3)若点P是平面内任意一动点,试确
定点P的位置.
2
.满足
(2)若点P是直线
上一动点,试确定点P的位置
.
交流展示
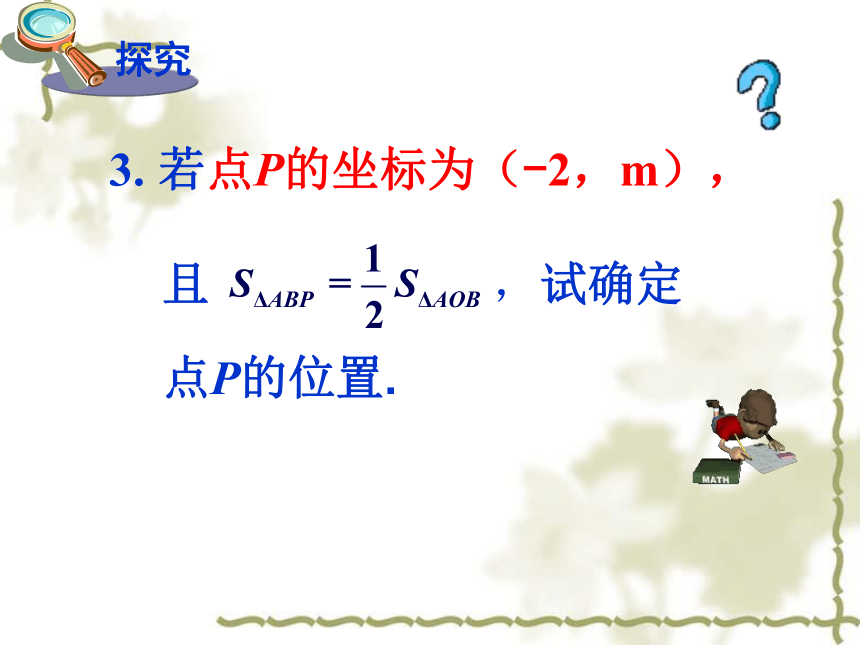
3.
若点P的坐标为(-2,m),
且
,试确定
点P的位置.
探究
已知直线L经过点(-2,4),且与坐标轴围成一
个等腰三角形,
(1)求直线的函数的解析式
(2)求所得三角形的周长及面积
注意:用坐标值表示线段长时要加上绝对值符号,以防漏解
引例
(1)设该直线的函数解析式为y=kx+b
把(-2,4)代入,得4=-2k+b,即b=2k+4
把x=0、y=0分别代入,得y=b=2k+4,x=-b/k=-2-4/k
由题意得|2k+4|=|-2-4/k|
当2k+4=-2-4/k时,整理得k?+3k+2=0
解得k1=-1,k2=-2
所以b1=2×(-1)+4=2,b2=2×(-2)+4=0(舍去)
当2k+4=2+4/k时,整理得k?+k-2=0
解得k3=1,k4=-2(舍去)
所以b3=2×1+4=6
所以该直线的函数解析式为y=-x+2或y=x+6
(2)当b=2时,三角形的周长为:2×2+2√2=4+2√2
三角形的面积为:1/2×2×2=2
当b=6时,三角形的周长为:6×2+6√2=12+6√2
三角形的面积为:1/2×6×6=18
一次函数的图像的应用
(面积问题)
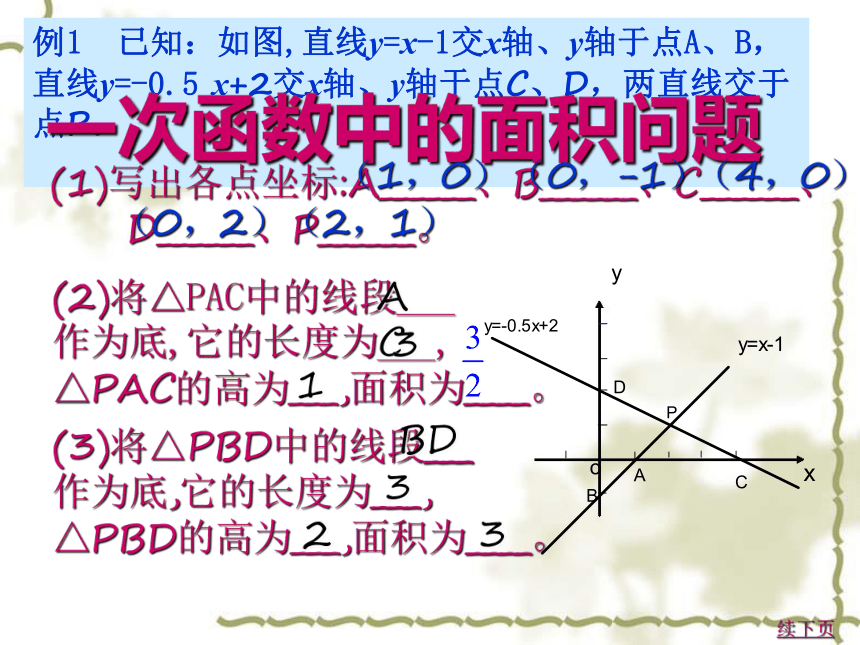
例1 已知:如图,直线y=x-1交x轴、y轴于点A、B, 直线y=-0.5
x+2交x轴、y轴于点C、D,两直线交于 点P。
续下页
一次函数中的面积问题
(1)写出各点坐标:A______、B______、C______、
D______、P______。
(1,0)
(0,-1)
(4,0)
(0,2)
(2,1)
(2)将△PAC中的线段___
作为底,它的长度为___,
△PAC的高为___,面积为____。
AC
3
1
(3)将△PBD中的线段___
作为底,它的长度为___,
△PBD的高为___,面积为____。
BD
3
2
3
返回
(4)
S四边形PAOD=_____-_____
=_____
S△COD
S△PAC
(5)
S△PBC=_____+_____
S△PBC=_____-_____=_____
S△PAC
S△BAC
S△PBD
S△CBD
3
如何求平面直角坐标系中的
图形的面积?
1.如果三角形有一边在坐标轴上(或平行于坐标轴),直接用面积公式求面积.
2.如果三角形任何一边都不在坐标轴上,也不平行于坐标轴,则需分割为几个有边在坐标轴上的三角形面积之和(或差).
3.四边形面积常转化为若干个三角形面积之和(或差).
例2 已知:直线y=2x和y=kx+b交于点A(1,m),直线y=kx+b交x轴于点B,且S△AOB=4。求m,k,b的值。
┐
A’
y=k’x
思考
(3):当点A(x,y)在线段
BC上
运动时,写出△AOB的面积s与
x的函数关系式,并写出自变量
的取值范围。
当点A运动到什么位置时,△AOB的
面积为3?
是否存在某一位置,使△AOB的面积为6?
思考
(4):若点A(x,y)在直线
BC上运动呢?
课堂小结
一、知识要点
1.求三角形面积的一般方法
(1)有一边在坐标轴上的三角形
(2)任何一边都不在坐标轴上,也不平行于坐标轴的三角形
2.四边形面积常转化为三角形面积之和或差
3.已知三角形面积求解析式,要注意多种情况
4.动点问题要充分考虑各种运动情况
二、思考策略
1.数形结合
2.转化
练习:
1、在直角坐标系中,
一次函数的图像与直线
平行,且图像与两坐标
轴围成的三角形面积等于4,求一次函数的
解析式。
2、已知正比例函数和一次函数的图像如图所示,其中交点A(3,4),且OA=
OB.求(1)正比例函数和一次函数解析式(2)三角形AOB的面积。
X
y
O
A
B
例:求直线
和
与y轴所
围成的图形的面积
例1
练习:
1、已知直线
与直线
的交点A在第四象限
(1)求正整数m的值;
(2)求交点A的坐标;
(3)求这两条直线与x轴所围成的三角形的面积
m=1
2、如图所示:直线y=kx+b经过点B
与点C(-1,3)且与x轴交与点A,经过点E(-2,0)的
直线与OC平行,并且与直线y=kx+b交与点D,
(1)求BC所在直线的函数解析式;(2)求点D的坐标;(3)求四边形CDEO的面积。
x
y
D
E
O
C
A
B
例2
总结
1、解题策略:画图像,看图像,求交点,分解图形
2、数学思想:数形结合思想。
练习与提高:
1:如图,由x轴,直线y=kx+4及分别过(1,0)
(3,0)且平行于y轴的两条直线所围成的梯形
ABCD的面积为
,求y=kx+4的解析式。
x
y
o
A
B
D
C
2、直线
:
y=kx+b过点B(-1,0)与y轴交于点C,
直线
:y=mx+n与
交于点P(2,5)且过点A
(6,0),过点C与
平行的直线交x轴于点D
(1)求直线CD的函数解析式;
(2)求四边形APCD的面积
B
C
P
A
X
Y
O
D
3、如图,已知长方形ABCD的边长AB=9,AD=3,现将此长方形置于坐标系中,使AB在x轴的正半轴上,经过点C的直线
与x轴交与点E,与y轴交与点F。
(1)求点E,B,D,A的坐标;(2)求四边形AECD
的面积。
y
o
F
A
D
C
B
E
x
变式:
如图:正方形ABCD边长为4,将此正方形置于坐标系
中点A的坐标为(1,0)。(1)过点C的直线
与x轴交与E,
求
(2)若直线l经过点E且将正方形
ABCD分成面积相等的两部分,求直线l的解析式。
Y
A
B
C
D
E
综合练习
1、已知一次函数y=kx+b的图像与反比例函数
y=a/x相交于A(2,4)B(-4,m)两点,(1)求两个
函数解析式。(2)求三角形AOB的面积。(3)
当一次函数的值大于反比例函数的值时,x的取值
2、P(a,b)是第一象限内在直线y=x-3上一点,已知A(0,4),三角形AOP的面积为S,(1)用b表示a
,(2)写出S关于b的解析式;(3)若三角形AOP的面积为10,求点P的坐标
例1、求直线y=2x+3、y=-2x-1及y轴围成的
三角形的面积
若将y轴改为x轴呢?
x
y
O
y=2x+1
y=-2x-1
A
B
C
D
P
例题精讲
例2、已知直线y=ax+
分别与x轴和y轴交于
B、C两点,直线y=-
x+b与x轴交于点A,并且两
直线交点P为(2,2)
(1)求两直线解析式;
(2)求四边形AOCP的面积.
x
y
O
A
B
P(2,2)
C
例3、如图,一次函数y=ax+b与正比例函数y=kx的图象交于第三象限内的点A,与y轴交于
点B(0,-4),且AO=AB,△AOB的面积为6,
求两函数解析式。
x
y
O
A
B(0,-4)
C
2
3
(-3,-2)
例4、一次函数图象与x轴的正半轴交于点A,与y轴的负半轴交于点B,与正比例函数
的图象交于点C,若OB=4,C点横坐标为6,(1)求一次函数的解析式;(2)求△AOB的面积;(3)求原点O到直线AB的距离。
x
y
o
C
A
B
(0,-4)
(6,
)
4
(3,0)
H
变式、已知:点P是一次函数y=-2x+8的图象上一点,如果图象与x轴交于Q点,且△OPQ的面积等于6,求P点的坐标。
x
y
o
y=-2x+8
Q
P
变式、若一次函数的图象交x轴于点A(-6,0),交正比例函数的图象于点B,且点B在第二象限,它的横坐标为-
4,又知:S△AOB=15,求直线AB的解析式。
x
y
o
A(-6,0)
(-4,
)
B
y
小结:
1、在求一次函数解析式时,一般有两个待定系数,因此,只要给出两个独立条件,就可求出它的解析式.当题目中出现角、长度等几何条件时,通常是把它转化为点的坐标后代入解析式,求出未知系数,得出函数解析式.
2、函数图象能直观、形象地反映两个变量之间的关系,要
善于捕捉图象中的所有信息,并能够熟练地转化成实际问题。
自学指导一:认真阅读试卷21题
如图,直线y=kx+6与x轴y轴分别相交于点E,F.点E的坐标为(-
9,
0),点A的坐标为(-6,0),点P(x,y)是第二象限内的直线上的一个动点。
(1)求k的值;
(2)当点P运动过程中,试写出△OPA的面积S与x的函数
关系式,并写出自变量x的取值范围;
(3)探究:当△OPA的面积为3.6时,求P的坐标。
A
F
O
E
y
x
p
解:
(1)将E(-9,0)代入y
=
kx+6
得-9k+6=0
3
2
得k=
A(-6,0)
过点P作PH
⊥OA
于H;
连结PA、PO
∵点P在第二象限内,且在直线EF上运动
F
O
E
y
∴-
9<x<0
x
H
OA=____,PH=______。
6
p
(x,y)
|y|
|
|
若点P(x,
y)
是第三象限内的直线上的一个动点;其他
当点P运动过程中,试写出△OPA的面积S与x
F
O
E
P(x,
)
----
H
A(-6,0)
变式(1):
自学检测1(3分钟)
条件不变。
的函数关系式,并写出自变量x的取值范围;
x
y
OA=____,PH=______。
6
(x<-9)
如图,直线y
=
kx+6与x轴y轴分别相交于点E,F.
点E的
坐标为(-
9,
0),
点A的坐标为(-
6,0).
点P(x,y)是
直线上y
=
kx+6(k≠0)的一个动点。
A
F
O
E
y
x
p
----
H
F
O
E
y
x
p
----
H
S=2x+18(-9S=-2x-18(x<-9)
如图,直线y
=
kx-6与x轴y轴分别相交于点E,F.
点E的
坐标为(12,
0),
点A的坐标为(8,0).
点P(x,y)是
直线上y
=
kx-6(k≠0)的一个动点。
点A的坐标为(-
6,0).
点P(x,y)是
第二象限内的直线上的一个动点。
如图,直线y
=
kx+6与x轴y轴分别相交于点E,F.
点E的
坐标为(-
9,
0),
(3)探究:当△OPA的面积为3.6时,求P的坐标
即2x+18=3.6
y
=
x+6
得,
3
2
y
=1.2
∴当△OPA的面积为3.6时,
P的坐标P(-7.2,1.2)
p
A
F
O
E
y
x
解:令S=3.6
将x=-7.2代入
解得x=-7.2
A
探究:当△OPA的面积为3.6时,求P的坐标
如图,直线y
=
kx+6与x轴y轴分别相交于点E,F.
点E的
坐标为(-
9,
0),
F
O
E
y
x
p
点A的坐标为(-
6,0).
点P(x,
y)是
第三象限内直线上的一个动点。
----
H
即-2x-18=3.6解得x=-10.8
y
=
-
x-6
得,
y
=-1.2
3
2
∴当△OPA的面积为3.6时,
P的坐标P(-10.8,-1.2)
变式(2):
将x=-10.8代入
解:令S=3.6
A
F
O
E
y
x
p
H
变式(1):
当点P在直线上运动过程中,若△OPA是以OA为底的等腰
三角形时,试求出点P坐标
变式(2):
在变式(1)的基础上平面内是否存在点D使以点A、O、P、
D为顶点的
四边形
是平行四边形,若存在直接写出点D的
坐标;若不存在请说明理由。
-------------------------
M
A
F
O
E
y
x
p
变式(3):
当点P在直线上运动过程中,若直线AP平分△OEF的面积
时,试求出直线AP的解析式和点P坐标
A
F
O
E
y
x
p
变式(6)
当点P在直线运动过程中,若直线AP分△OEF的面积为1:2
两部分时,试求出直线AP的解析式和点P坐标
A
F
O
E
y
x
p
A
F
O
E
y
x
p
变式(7):
当点P在第一和第二象限内(y轴上除外)运动过程中,
试写出以O、F、P、A为顶点的四边形的面积S与x的
函数关系式并指出自变量x的取值范围。
-----------
H
A
F
O
E
y
x
p
----------------------
当点P在直线上运动,
试写出以O、F、P、A为顶点的四边形的面积S与x的
函数关系式并指出自变量x的取值范围。
如图,直线y
=
kx-6与x轴y轴分别相交于点E,F.
点E的
坐标为(-
9,
0),
变式(8):
当点P在直线上运动,
试写出以O、F、P、A为顶点的四边形的面积S与x的
函数关系式并指出自变量x的取值范围。
A
F
O
E
y
x
p
如图,直线y
=
kx-6与x轴y轴分别相交于点E,F.
点E的
坐标为(-
9,
0),
变式(8):
E
A
O
F
p
一次函数的面积问题
第十九章
一次函数
复习与回顾
2、求直线
与两坐标轴所围成的
三角形的面积.
1、已知一次函数
的图像平行
于直线
,且过点(-1,5),
求一次函数的
解析式.
3、将直线
平移,使其经过(4,3)
(1)求平移后的函数解析式
(2)求平移后的函数图像与两坐标轴围成的三角形面积
6
1.
已知一次函数
.
(1)求图象与x轴交点A,
与y轴交点B的坐标.
(2)求图象与坐标轴所围成的三角形面积.
解:
(2)SΔOAB
=
OA·OB
=4
(1)设
与
轴交点坐标A(-2,0)
设
与
轴交点坐标B(0,4)
复习引入
2、求直线y=-1.5x+3与x轴、y轴所围成的三角形的面积。
y
x
O
A
B
3
2
解:当x=0时,y=3;
当y=0时,x=2;
∴A(0,3) B(2,0)
∴OA=3,OB=2
因此三角形的面积为3.
∴S△ABC= OA·OB
=
×3×2=3
求直线y=kx+b与x轴、y轴所围成的三角形的面积。
y
x
O
A
B
b
∴S△ABC=
知识探究
解:当x=0时,y=b;
当y=0时,x=
;
∴A(0,b), B(
,0)
∴OA=|b|,OB=
=
×
OA·OB
×|b|×
=
=
1.
若点P是
x
轴上一个动点,
且
,试确定
点P的位置.
探究
(1)若点P是y轴上一动点,
试确定点P的位置.
(3)若点P是平面内任意一动点,试确
定点P的位置.
2
.满足
(2)若点P是直线
上一动点,试确定点P的位置
.
交流展示
3.
若点P的坐标为(-2,m),
且
,试确定
点P的位置.
探究
已知直线L经过点(-2,4),且与坐标轴围成一
个等腰三角形,
(1)求直线的函数的解析式
(2)求所得三角形的周长及面积
注意:用坐标值表示线段长时要加上绝对值符号,以防漏解
引例
(1)设该直线的函数解析式为y=kx+b
把(-2,4)代入,得4=-2k+b,即b=2k+4
把x=0、y=0分别代入,得y=b=2k+4,x=-b/k=-2-4/k
由题意得|2k+4|=|-2-4/k|
当2k+4=-2-4/k时,整理得k?+3k+2=0
解得k1=-1,k2=-2
所以b1=2×(-1)+4=2,b2=2×(-2)+4=0(舍去)
当2k+4=2+4/k时,整理得k?+k-2=0
解得k3=1,k4=-2(舍去)
所以b3=2×1+4=6
所以该直线的函数解析式为y=-x+2或y=x+6
(2)当b=2时,三角形的周长为:2×2+2√2=4+2√2
三角形的面积为:1/2×2×2=2
当b=6时,三角形的周长为:6×2+6√2=12+6√2
三角形的面积为:1/2×6×6=18
一次函数的图像的应用
(面积问题)
例1 已知:如图,直线y=x-1交x轴、y轴于点A、B, 直线y=-0.5
x+2交x轴、y轴于点C、D,两直线交于 点P。
续下页
一次函数中的面积问题
(1)写出各点坐标:A______、B______、C______、
D______、P______。
(1,0)
(0,-1)
(4,0)
(0,2)
(2,1)
(2)将△PAC中的线段___
作为底,它的长度为___,
△PAC的高为___,面积为____。
AC
3
1
(3)将△PBD中的线段___
作为底,它的长度为___,
△PBD的高为___,面积为____。
BD
3
2
3
返回
(4)
S四边形PAOD=_____-_____
=_____
S△COD
S△PAC
(5)
S△PBC=_____+_____
S△PBC=_____-_____=_____
S△PAC
S△BAC
S△PBD
S△CBD
3
如何求平面直角坐标系中的
图形的面积?
1.如果三角形有一边在坐标轴上(或平行于坐标轴),直接用面积公式求面积.
2.如果三角形任何一边都不在坐标轴上,也不平行于坐标轴,则需分割为几个有边在坐标轴上的三角形面积之和(或差).
3.四边形面积常转化为若干个三角形面积之和(或差).
例2 已知:直线y=2x和y=kx+b交于点A(1,m),直线y=kx+b交x轴于点B,且S△AOB=4。求m,k,b的值。
┐
A’
y=k’x
思考
(3):当点A(x,y)在线段
BC上
运动时,写出△AOB的面积s与
x的函数关系式,并写出自变量
的取值范围。
当点A运动到什么位置时,△AOB的
面积为3?
是否存在某一位置,使△AOB的面积为6?
思考
(4):若点A(x,y)在直线
BC上运动呢?
课堂小结
一、知识要点
1.求三角形面积的一般方法
(1)有一边在坐标轴上的三角形
(2)任何一边都不在坐标轴上,也不平行于坐标轴的三角形
2.四边形面积常转化为三角形面积之和或差
3.已知三角形面积求解析式,要注意多种情况
4.动点问题要充分考虑各种运动情况
二、思考策略
1.数形结合
2.转化
练习:
1、在直角坐标系中,
一次函数的图像与直线
平行,且图像与两坐标
轴围成的三角形面积等于4,求一次函数的
解析式。
2、已知正比例函数和一次函数的图像如图所示,其中交点A(3,4),且OA=
OB.求(1)正比例函数和一次函数解析式(2)三角形AOB的面积。
X
y
O
A
B
例:求直线
和
与y轴所
围成的图形的面积
例1
练习:
1、已知直线
与直线
的交点A在第四象限
(1)求正整数m的值;
(2)求交点A的坐标;
(3)求这两条直线与x轴所围成的三角形的面积
m=1
2、如图所示:直线y=kx+b经过点B
与点C(-1,3)且与x轴交与点A,经过点E(-2,0)的
直线与OC平行,并且与直线y=kx+b交与点D,
(1)求BC所在直线的函数解析式;(2)求点D的坐标;(3)求四边形CDEO的面积。
x
y
D
E
O
C
A
B
例2
总结
1、解题策略:画图像,看图像,求交点,分解图形
2、数学思想:数形结合思想。
练习与提高:
1:如图,由x轴,直线y=kx+4及分别过(1,0)
(3,0)且平行于y轴的两条直线所围成的梯形
ABCD的面积为
,求y=kx+4的解析式。
x
y
o
A
B
D
C
2、直线
:
y=kx+b过点B(-1,0)与y轴交于点C,
直线
:y=mx+n与
交于点P(2,5)且过点A
(6,0),过点C与
平行的直线交x轴于点D
(1)求直线CD的函数解析式;
(2)求四边形APCD的面积
B
C
P
A
X
Y
O
D
3、如图,已知长方形ABCD的边长AB=9,AD=3,现将此长方形置于坐标系中,使AB在x轴的正半轴上,经过点C的直线
与x轴交与点E,与y轴交与点F。
(1)求点E,B,D,A的坐标;(2)求四边形AECD
的面积。
y
o
F
A
D
C
B
E
x
变式:
如图:正方形ABCD边长为4,将此正方形置于坐标系
中点A的坐标为(1,0)。(1)过点C的直线
与x轴交与E,
求
(2)若直线l经过点E且将正方形
ABCD分成面积相等的两部分,求直线l的解析式。
Y
A
B
C
D
E
综合练习
1、已知一次函数y=kx+b的图像与反比例函数
y=a/x相交于A(2,4)B(-4,m)两点,(1)求两个
函数解析式。(2)求三角形AOB的面积。(3)
当一次函数的值大于反比例函数的值时,x的取值
2、P(a,b)是第一象限内在直线y=x-3上一点,已知A(0,4),三角形AOP的面积为S,(1)用b表示a
,(2)写出S关于b的解析式;(3)若三角形AOP的面积为10,求点P的坐标
例1、求直线y=2x+3、y=-2x-1及y轴围成的
三角形的面积
若将y轴改为x轴呢?
x
y
O
y=2x+1
y=-2x-1
A
B
C
D
P
例题精讲
例2、已知直线y=ax+
分别与x轴和y轴交于
B、C两点,直线y=-
x+b与x轴交于点A,并且两
直线交点P为(2,2)
(1)求两直线解析式;
(2)求四边形AOCP的面积.
x
y
O
A
B
P(2,2)
C
例3、如图,一次函数y=ax+b与正比例函数y=kx的图象交于第三象限内的点A,与y轴交于
点B(0,-4),且AO=AB,△AOB的面积为6,
求两函数解析式。
x
y
O
A
B(0,-4)
C
2
3
(-3,-2)
例4、一次函数图象与x轴的正半轴交于点A,与y轴的负半轴交于点B,与正比例函数
的图象交于点C,若OB=4,C点横坐标为6,(1)求一次函数的解析式;(2)求△AOB的面积;(3)求原点O到直线AB的距离。
x
y
o
C
A
B
(0,-4)
(6,
)
4
(3,0)
H
变式、已知:点P是一次函数y=-2x+8的图象上一点,如果图象与x轴交于Q点,且△OPQ的面积等于6,求P点的坐标。
x
y
o
y=-2x+8
Q
P
变式、若一次函数的图象交x轴于点A(-6,0),交正比例函数的图象于点B,且点B在第二象限,它的横坐标为-
4,又知:S△AOB=15,求直线AB的解析式。
x
y
o
A(-6,0)
(-4,
)
B
y
小结:
1、在求一次函数解析式时,一般有两个待定系数,因此,只要给出两个独立条件,就可求出它的解析式.当题目中出现角、长度等几何条件时,通常是把它转化为点的坐标后代入解析式,求出未知系数,得出函数解析式.
2、函数图象能直观、形象地反映两个变量之间的关系,要
善于捕捉图象中的所有信息,并能够熟练地转化成实际问题。
自学指导一:认真阅读试卷21题
如图,直线y=kx+6与x轴y轴分别相交于点E,F.点E的坐标为(-
9,
0),点A的坐标为(-6,0),点P(x,y)是第二象限内的直线上的一个动点。
(1)求k的值;
(2)当点P运动过程中,试写出△OPA的面积S与x的函数
关系式,并写出自变量x的取值范围;
(3)探究:当△OPA的面积为3.6时,求P的坐标。
A
F
O
E
y
x
p
解:
(1)将E(-9,0)代入y
=
kx+6
得-9k+6=0
3
2
得k=
A(-6,0)
过点P作PH
⊥OA
于H;
连结PA、PO
∵点P在第二象限内,且在直线EF上运动
F
O
E
y
∴-
9<x<0
x
H
OA=____,PH=______。
6
p
(x,y)
|y|
|
|
若点P(x,
y)
是第三象限内的直线上的一个动点;其他
当点P运动过程中,试写出△OPA的面积S与x
F
O
E
P(x,
)
----
H
A(-6,0)
变式(1):
自学检测1(3分钟)
条件不变。
的函数关系式,并写出自变量x的取值范围;
x
y
OA=____,PH=______。
6
(x<-9)
如图,直线y
=
kx+6与x轴y轴分别相交于点E,F.
点E的
坐标为(-
9,
0),
点A的坐标为(-
6,0).
点P(x,y)是
直线上y
=
kx+6(k≠0)的一个动点。
A
F
O
E
y
x
p
----
H
F
O
E
y
x
p
----
H
S=2x+18(-9
如图,直线y
=
kx-6与x轴y轴分别相交于点E,F.
点E的
坐标为(12,
0),
点A的坐标为(8,0).
点P(x,y)是
直线上y
=
kx-6(k≠0)的一个动点。
点A的坐标为(-
6,0).
点P(x,y)是
第二象限内的直线上的一个动点。
如图,直线y
=
kx+6与x轴y轴分别相交于点E,F.
点E的
坐标为(-
9,
0),
(3)探究:当△OPA的面积为3.6时,求P的坐标
即2x+18=3.6
y
=
x+6
得,
3
2
y
=1.2
∴当△OPA的面积为3.6时,
P的坐标P(-7.2,1.2)
p
A
F
O
E
y
x
解:令S=3.6
将x=-7.2代入
解得x=-7.2
A
探究:当△OPA的面积为3.6时,求P的坐标
如图,直线y
=
kx+6与x轴y轴分别相交于点E,F.
点E的
坐标为(-
9,
0),
F
O
E
y
x
p
点A的坐标为(-
6,0).
点P(x,
y)是
第三象限内直线上的一个动点。
----
H
即-2x-18=3.6解得x=-10.8
y
=
-
x-6
得,
y
=-1.2
3
2
∴当△OPA的面积为3.6时,
P的坐标P(-10.8,-1.2)
变式(2):
将x=-10.8代入
解:令S=3.6
A
F
O
E
y
x
p
H
变式(1):
当点P在直线上运动过程中,若△OPA是以OA为底的等腰
三角形时,试求出点P坐标
变式(2):
在变式(1)的基础上平面内是否存在点D使以点A、O、P、
D为顶点的
四边形
是平行四边形,若存在直接写出点D的
坐标;若不存在请说明理由。
-------------------------
M
A
F
O
E
y
x
p
变式(3):
当点P在直线上运动过程中,若直线AP平分△OEF的面积
时,试求出直线AP的解析式和点P坐标
A
F
O
E
y
x
p
变式(6)
当点P在直线运动过程中,若直线AP分△OEF的面积为1:2
两部分时,试求出直线AP的解析式和点P坐标
A
F
O
E
y
x
p
A
F
O
E
y
x
p
变式(7):
当点P在第一和第二象限内(y轴上除外)运动过程中,
试写出以O、F、P、A为顶点的四边形的面积S与x的
函数关系式并指出自变量x的取值范围。
-----------
H
A
F
O
E
y
x
p
----------------------
当点P在直线上运动,
试写出以O、F、P、A为顶点的四边形的面积S与x的
函数关系式并指出自变量x的取值范围。
如图,直线y
=
kx-6与x轴y轴分别相交于点E,F.
点E的
坐标为(-
9,
0),
变式(8):
当点P在直线上运动,
试写出以O、F、P、A为顶点的四边形的面积S与x的
函数关系式并指出自变量x的取值范围。
A
F
O
E
y
x
p
如图,直线y
=
kx-6与x轴y轴分别相交于点E,F.
点E的
坐标为(-
9,
0),
变式(8):
E
A
O
F
p
