2020-2021学年人教版七年级数学下册8.3实际问题与二元一次方程组课件(共17张ppt)
文档属性
| 名称 | 2020-2021学年人教版七年级数学下册8.3实际问题与二元一次方程组课件(共17张ppt) |

|
|
| 格式 | zip | ||
| 文件大小 | 3.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-04-20 00:00:00 | ||
图片预览






文档简介
(共17张PPT)
8.3实际问题与二元一次方程组(1)
导入
情境导入
引入新知
养牛场原有30头大牛和15头小牛,1天约需要饲料675kg;一周后又购进12头大牛和5头小牛,这时1天约需要饲料940kg。饲养员李大叔估计平均每
头大牛1天约需饲料18至20kg,每头小牛1天约需要饲料7至8kg。请你通过计算检验李大叔的估计是否正确?
第一站:养殖基地
解:设平均每头大牛和每头小牛1天各约需饲料xkg和ykg.
试一试:找出题目中的相等关系,并根据等量关系设未知数、列方程组解答出来。
解得:
20
5
思考:根据计算结果可以
判断李大叔的估计如何?
这就是说,每头大牛约需饲料20kg,每头小牛约需饲料5kg.因此,饲料员李大叔对大牛的食量估计较准确,对小牛的食量估计偏高.
探究1
探究新知
小组交流合作完成
?
í
ì
=
+
675
5
1
30
y
x
12
+5
=940-675
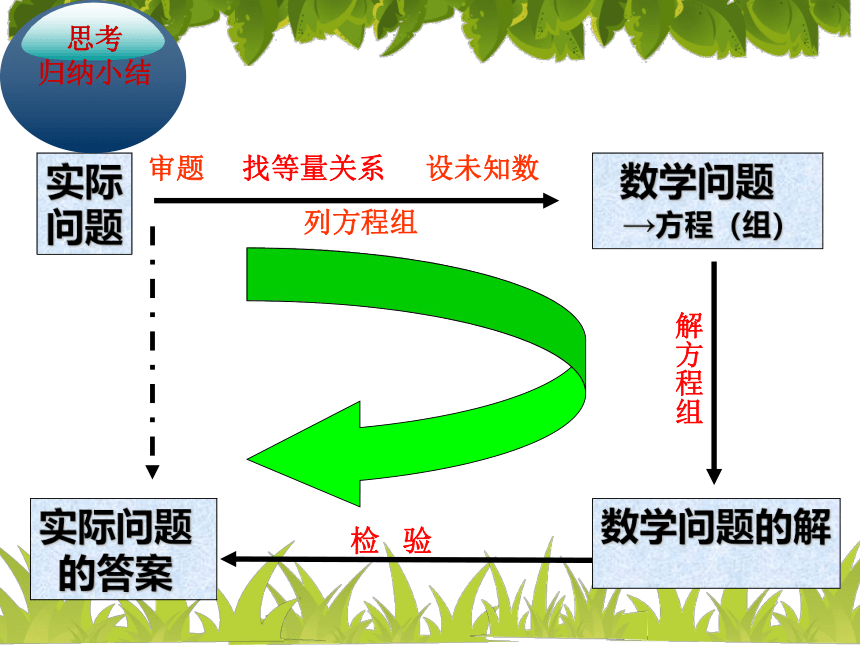
实际
问题
数学问题
→方程(组)
解方程组
数学问题的解
检
验
实际问题
的答案
思考
归纳小结
审题
找等量关系
设未知数
列方程组
练一练:旅游点共有2个大餐厅和2个小餐厅,同时开放1个大餐厅和2个小餐厅,可供110人就餐;同时开放2个大餐厅和1个小餐厅,可供130人就餐。若4个餐厅同时开放,请估计一下能否供应180个游人同时餐?
练一练:旅游点共有2个大餐厅和2个小餐厅,同时开放1个大餐厅和2个小餐厅,可供110人就餐;同时开放2个大餐厅和1个小餐厅,可供130人就餐。若4个餐厅同时开放,请估计一下能否供应180个游人人同时就餐?
解:设1个大餐厅可供x人就餐,1个小餐厅可供y人就餐,则
x+2y=110
2x+y=130
解得:
x=50
y=30
50x2+30x2=160<180
答:4个餐厅同时开放不能供应180人。
1、把长方形纸片折成面积相等的两个小长方形,
有哪些折法?
2、把长方形纸片折成面积之比为1:2的两个小长方形,
又有哪些折法?
●
●
●
●
分割长方形面积的问题
可转化为分割长方形边长的问题。
游戏
折一折
据以往的统计资料,甲、乙两种作物的单位面积产量的比是1:2
,现要在一块长为200m,宽为100m的长方形土地上种植这两种作物,怎样把这块地分为两个长方形,使甲、乙两种作物的总产量的比是3:4
?
探究2
探究新知
第二站:种植基地
200
100
A
B
C
D
E
F
甲
乙
1
2
x
x
说一说:什么是单位面积?什么是单位面积的产量呢?如何解释甲乙两种作物单位面积的产量的比是1:2
?
甲乙两种作物的总产量用式子怎样表示?
小组合作交流:根据以上的分析,找出
等量关系,列出方程组,并解答
200
100
A
B
C
D
E
F
甲
乙
1
2
x
x
)
:
=
3︰4
解:一种种植方案为:甲乙两种作物的种植区域分别为长方形AEFD和BCFE,设AE=xm,BE=ym
+
=
200
(
解得
=120
=
80
如何表述你的种植方法?
∴
过长方形土地的长边上离一端约120m处,
作这条边的垂线把这块地分为两个长方形,
较大一块地种甲作物,较小一块地种乙作物.
(
)
想一想,议一议,还有其他设计方案吗?
200
100
A
B
C
D
M
N
X+y=100
200x:(2x200y)=3:4
200
200
x1
x2
200
100
A
B
C
D
E
F
甲
乙
2
3
x
x
)
:
=
3︰4
+
=
200
(
(
)
变式:若将上题中的条件:甲、乙两种作物的单位面积产量
的比是1:2变为甲、乙两种作物的单位面积产量的比是2:3,
其它条件不变,你能列出方程组吗?
本节课你有哪些收获?
还有哪些困惑?
课堂小结
一种方法
用二元一次方程组
解决实际问题的方法
一种思想
建模思想
我的收获
教科书习题8.3第2、3、4、5题
布置作业
?
í
ì
=
+
675
5
1
30
y
x
12
+5
=900-675
8.3实际问题与二元一次方程组(1)
导入
情境导入
引入新知
养牛场原有30头大牛和15头小牛,1天约需要饲料675kg;一周后又购进12头大牛和5头小牛,这时1天约需要饲料940kg。饲养员李大叔估计平均每
头大牛1天约需饲料18至20kg,每头小牛1天约需要饲料7至8kg。请你通过计算检验李大叔的估计是否正确?
第一站:养殖基地
解:设平均每头大牛和每头小牛1天各约需饲料xkg和ykg.
试一试:找出题目中的相等关系,并根据等量关系设未知数、列方程组解答出来。
解得:
20
5
思考:根据计算结果可以
判断李大叔的估计如何?
这就是说,每头大牛约需饲料20kg,每头小牛约需饲料5kg.因此,饲料员李大叔对大牛的食量估计较准确,对小牛的食量估计偏高.
探究1
探究新知
小组交流合作完成
?
í
ì
=
+
675
5
1
30
y
x
12
+5
=940-675
实际
问题
数学问题
→方程(组)
解方程组
数学问题的解
检
验
实际问题
的答案
思考
归纳小结
审题
找等量关系
设未知数
列方程组
练一练:旅游点共有2个大餐厅和2个小餐厅,同时开放1个大餐厅和2个小餐厅,可供110人就餐;同时开放2个大餐厅和1个小餐厅,可供130人就餐。若4个餐厅同时开放,请估计一下能否供应180个游人同时餐?
练一练:旅游点共有2个大餐厅和2个小餐厅,同时开放1个大餐厅和2个小餐厅,可供110人就餐;同时开放2个大餐厅和1个小餐厅,可供130人就餐。若4个餐厅同时开放,请估计一下能否供应180个游人人同时就餐?
解:设1个大餐厅可供x人就餐,1个小餐厅可供y人就餐,则
x+2y=110
2x+y=130
解得:
x=50
y=30
50x2+30x2=160<180
答:4个餐厅同时开放不能供应180人。
1、把长方形纸片折成面积相等的两个小长方形,
有哪些折法?
2、把长方形纸片折成面积之比为1:2的两个小长方形,
又有哪些折法?
●
●
●
●
分割长方形面积的问题
可转化为分割长方形边长的问题。
游戏
折一折
据以往的统计资料,甲、乙两种作物的单位面积产量的比是1:2
,现要在一块长为200m,宽为100m的长方形土地上种植这两种作物,怎样把这块地分为两个长方形,使甲、乙两种作物的总产量的比是3:4
?
探究2
探究新知
第二站:种植基地
200
100
A
B
C
D
E
F
甲
乙
1
2
x
x
说一说:什么是单位面积?什么是单位面积的产量呢?如何解释甲乙两种作物单位面积的产量的比是1:2
?
甲乙两种作物的总产量用式子怎样表示?
小组合作交流:根据以上的分析,找出
等量关系,列出方程组,并解答
200
100
A
B
C
D
E
F
甲
乙
1
2
x
x
)
:
=
3︰4
解:一种种植方案为:甲乙两种作物的种植区域分别为长方形AEFD和BCFE,设AE=xm,BE=ym
+
=
200
(
解得
=120
=
80
如何表述你的种植方法?
∴
过长方形土地的长边上离一端约120m处,
作这条边的垂线把这块地分为两个长方形,
较大一块地种甲作物,较小一块地种乙作物.
(
)
想一想,议一议,还有其他设计方案吗?
200
100
A
B
C
D
M
N
X+y=100
200x:(2x200y)=3:4
200
200
x1
x2
200
100
A
B
C
D
E
F
甲
乙
2
3
x
x
)
:
=
3︰4
+
=
200
(
(
)
变式:若将上题中的条件:甲、乙两种作物的单位面积产量
的比是1:2变为甲、乙两种作物的单位面积产量的比是2:3,
其它条件不变,你能列出方程组吗?
本节课你有哪些收获?
还有哪些困惑?
课堂小结
一种方法
用二元一次方程组
解决实际问题的方法
一种思想
建模思想
我的收获
教科书习题8.3第2、3、4、5题
布置作业
?
í
ì
=
+
675
5
1
30
y
x
12
+5
=900-675
