2020--2021学年人教版七年级数学下册课件-6.3 实数 22(共15张ppt)
文档属性
| 名称 | 2020--2021学年人教版七年级数学下册课件-6.3 实数 22(共15张ppt) |  | |
| 格式 | zip | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-04-20 06:50:12 | ||
图片预览






文档简介
(共15张PPT)
人教版七年级数学下册
6.3
实
数(1)
课题引入
吊环王陈一冰
在男子吊环中以
16.600分,为中国夺得第36枚金牌.
郭晶晶/吴敏霞
在女子双人3米跳板以343.50分,为中国夺得第4枚金牌.
活动探究
学习目标
课题引入
讲授新课
巩固练习
课堂小结
布置作业
例题讲解
知识反馈
(1)了解无理数和实数的概念以及实
数的分类
(2)会判断一个数是无理数还是有理
数
学习目标
(3)知道实数与数轴上的点具有一
一对应的关系
活动探究
学习目标
课题引入
讲授新课
巩固练习
课堂小结
布置作业
例题讲解
知识反馈
讲授新课
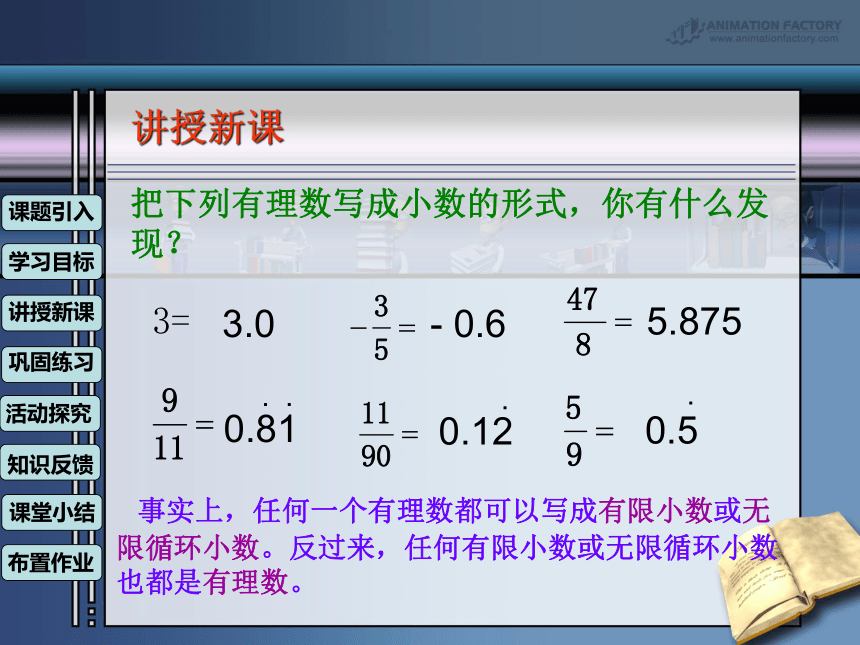
把下列有理数写成小数的形式,你有什么发现?
事实上,任何一个有理数都可以写成有限小数或无限循环小数。反过来,任何有限小数或无限循环小数也都是有理数。
3=
3.0
-
0.6
5.875
0.81
.
.
0.12
.
0.5
.
活动探究
学习目标
课题引入
讲授新课
巩固练习
课堂小结
布置作业
例题讲解
知识反馈
讲授新课
=
3.14159265358
…
无限不循环的小数
你能举出一些无理数吗?
带根号的数都是无理数对吗
?
=
-
2.236067977
…
=
-
1.709975947
…
=
1.414213562…
叫做无理数
活动探究
学习目标
课题引入
讲授新课
巩固练习
课堂小结
布置作业
例题讲解
知识反馈
讲授新课
实数
有理数
无理数
正实数
0
负实数
正有理数
正无理数
负有理数
负无理数
分数
整数
有限小数或
无限循环小数
无限不循环小数
实数
活动探究
学习目标
课题引入
讲授新课
巩固练习
课堂小结
布置作业
例题讲解
知识反馈
巩固练习
把下列各数填入相应的集合内:
(1)有理数集合:
(2)无理数集合:
(3)正实数集合:
活动探究
学习目标
课题引入
讲授新课
巩固练习
课堂小结
布置作业
例题讲解
知识反馈
(4)
负实数集合:
4
4
0.15
0.15
-7.5
-7.5
活动探究
每个有理数都可以用数轴上的点表示,那么无理数是否也可以用数轴上的点表示出来吗?
1、能在数轴上找到表示π的点吗?
[
演示
1
]
2、你能把
表示出来吗?与你同桌讨论.
也就是说:每一个无理数都可以用数轴上的一个点来表示.数轴上的点有些表示有理数,有些表示无理数.
[
演示
2
]
活动探究
学习目标
课题引入
讲授新课
巩固练习
课堂小结
布置作业
例题讲解
知识反馈
当数从有理数扩充到实数以后,实数与数轴上的点就是一一对应的,即每一个实数都可以用数轴上的一个点来表示;反过来,数轴上的每一个点都表示一个实数.
活动探究
活动探究
学习目标
课题引入
讲授新课
巩固练习
课堂小结
布置作业
例题讲解
知识反馈
同样的,平面直角坐标系中的点与有序实数对是一一对应的.
(
2
,1
)
给出坐标(2,1)你能在平面直角坐标系中找到这一点吗?
0
-2
4
-1
2
1
3
1
2
3
-1
-2
A
x
y
活动探究
活动探究
学习目标
课题引入
讲授新课
巩固练习
课堂小结
布置作业
例题讲解
知识反馈
知识反馈
一、请将数轴上的各点与下列实数对应起来
0
-2
4
A
E
D
C
B
-1.5
π
3
二、(中考热点)在
这六个实数中,无理数的个数是(
)
A、4个
B、3个
C、2个
D、1个
活动探究
学习目标
课题引入
讲授新课
巩固练习
课堂小结
布置作业
例题讲解
知识反馈
C
知识反馈
三、判断
1.实数不是有理数就是无理数。(
)
2.无理数都是无限小数。(
)
3.无理数一定都带根号。(
)
4.带根号的数都是无理数。(
)
5.无理数都是无限不循环小数。(
)
6.无限小数都是无理数。(
)
×
×
×
活动探究
学习目标
课题引入
讲授新课
巩固练习
课堂小结
布置作业
例题讲解
知识反馈
这节课你有什么收获?
课堂小结
活动探究
学习目标
课题引入
讲授新课
巩固练习
课堂小结
布置作业
例题讲解
知识反馈
布置作业
课
本
P86
习
题
13.3
1、2
活动探究
学习目标
课题引入
讲授新课
巩固练习
课堂小结
布置作业
例题讲解
知识反馈
人教版八年级数学上册
再
见
!
人教版七年级数学下册
6.3
实
数(1)
课题引入
吊环王陈一冰
在男子吊环中以
16.600分,为中国夺得第36枚金牌.
郭晶晶/吴敏霞
在女子双人3米跳板以343.50分,为中国夺得第4枚金牌.
活动探究
学习目标
课题引入
讲授新课
巩固练习
课堂小结
布置作业
例题讲解
知识反馈
(1)了解无理数和实数的概念以及实
数的分类
(2)会判断一个数是无理数还是有理
数
学习目标
(3)知道实数与数轴上的点具有一
一对应的关系
活动探究
学习目标
课题引入
讲授新课
巩固练习
课堂小结
布置作业
例题讲解
知识反馈
讲授新课
把下列有理数写成小数的形式,你有什么发现?
事实上,任何一个有理数都可以写成有限小数或无限循环小数。反过来,任何有限小数或无限循环小数也都是有理数。
3=
3.0
-
0.6
5.875
0.81
.
.
0.12
.
0.5
.
活动探究
学习目标
课题引入
讲授新课
巩固练习
课堂小结
布置作业
例题讲解
知识反馈
讲授新课
=
3.14159265358
…
无限不循环的小数
你能举出一些无理数吗?
带根号的数都是无理数对吗
?
=
-
2.236067977
…
=
-
1.709975947
…
=
1.414213562…
叫做无理数
活动探究
学习目标
课题引入
讲授新课
巩固练习
课堂小结
布置作业
例题讲解
知识反馈
讲授新课
实数
有理数
无理数
正实数
0
负实数
正有理数
正无理数
负有理数
负无理数
分数
整数
有限小数或
无限循环小数
无限不循环小数
实数
活动探究
学习目标
课题引入
讲授新课
巩固练习
课堂小结
布置作业
例题讲解
知识反馈
巩固练习
把下列各数填入相应的集合内:
(1)有理数集合:
(2)无理数集合:
(3)正实数集合:
活动探究
学习目标
课题引入
讲授新课
巩固练习
课堂小结
布置作业
例题讲解
知识反馈
(4)
负实数集合:
4
4
0.15
0.15
-7.5
-7.5
活动探究
每个有理数都可以用数轴上的点表示,那么无理数是否也可以用数轴上的点表示出来吗?
1、能在数轴上找到表示π的点吗?
[
演示
1
]
2、你能把
表示出来吗?与你同桌讨论.
也就是说:每一个无理数都可以用数轴上的一个点来表示.数轴上的点有些表示有理数,有些表示无理数.
[
演示
2
]
活动探究
学习目标
课题引入
讲授新课
巩固练习
课堂小结
布置作业
例题讲解
知识反馈
当数从有理数扩充到实数以后,实数与数轴上的点就是一一对应的,即每一个实数都可以用数轴上的一个点来表示;反过来,数轴上的每一个点都表示一个实数.
活动探究
活动探究
学习目标
课题引入
讲授新课
巩固练习
课堂小结
布置作业
例题讲解
知识反馈
同样的,平面直角坐标系中的点与有序实数对是一一对应的.
(
2
,1
)
给出坐标(2,1)你能在平面直角坐标系中找到这一点吗?
0
-2
4
-1
2
1
3
1
2
3
-1
-2
A
x
y
活动探究
活动探究
学习目标
课题引入
讲授新课
巩固练习
课堂小结
布置作业
例题讲解
知识反馈
知识反馈
一、请将数轴上的各点与下列实数对应起来
0
-2
4
A
E
D
C
B
-1.5
π
3
二、(中考热点)在
这六个实数中,无理数的个数是(
)
A、4个
B、3个
C、2个
D、1个
活动探究
学习目标
课题引入
讲授新课
巩固练习
课堂小结
布置作业
例题讲解
知识反馈
C
知识反馈
三、判断
1.实数不是有理数就是无理数。(
)
2.无理数都是无限小数。(
)
3.无理数一定都带根号。(
)
4.带根号的数都是无理数。(
)
5.无理数都是无限不循环小数。(
)
6.无限小数都是无理数。(
)
×
×
×
活动探究
学习目标
课题引入
讲授新课
巩固练习
课堂小结
布置作业
例题讲解
知识反馈
这节课你有什么收获?
课堂小结
活动探究
学习目标
课题引入
讲授新课
巩固练习
课堂小结
布置作业
例题讲解
知识反馈
布置作业
课
本
P86
习
题
13.3
1、2
活动探究
学习目标
课题引入
讲授新课
巩固练习
课堂小结
布置作业
例题讲解
知识反馈
人教版八年级数学上册
再
见
!
