18.2.3正方形判定 课件-2020-2021学年人教版八年级数学下册(共16张ppt)
文档属性
| 名称 | 18.2.3正方形判定 课件-2020-2021学年人教版八年级数学下册(共16张ppt) |

|
|
| 格式 | zip | ||
| 文件大小 | 769.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-04-19 21:46:43 | ||
图片预览

文档简介
(共16张PPT)
空白演示
单击输入您的封面副标题
18.2.3
正方形的判定
人教
版八年级数学下册
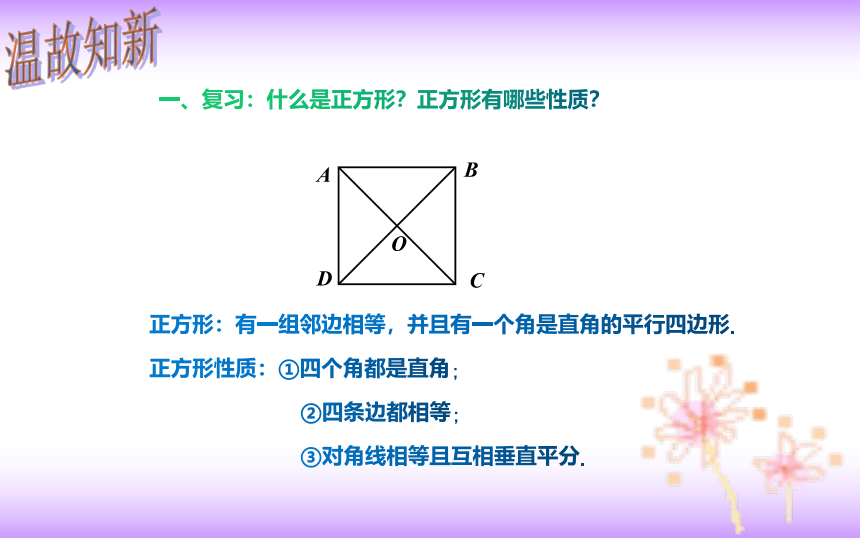
一、复习:什么是正方形?正方形有哪些性质?
A
B
C
D
正方形:有一组邻边相等,并且有一个角是直角的平行四边形.
正方形性质:①四个角都是直角;
②四条边都相等;
③对角线相等且互相垂直平分.
O
温故知新
5种判定方法
三个角是直角
四条边相等
一个角是直角
对角线相等
一组邻边相等
对角线垂直
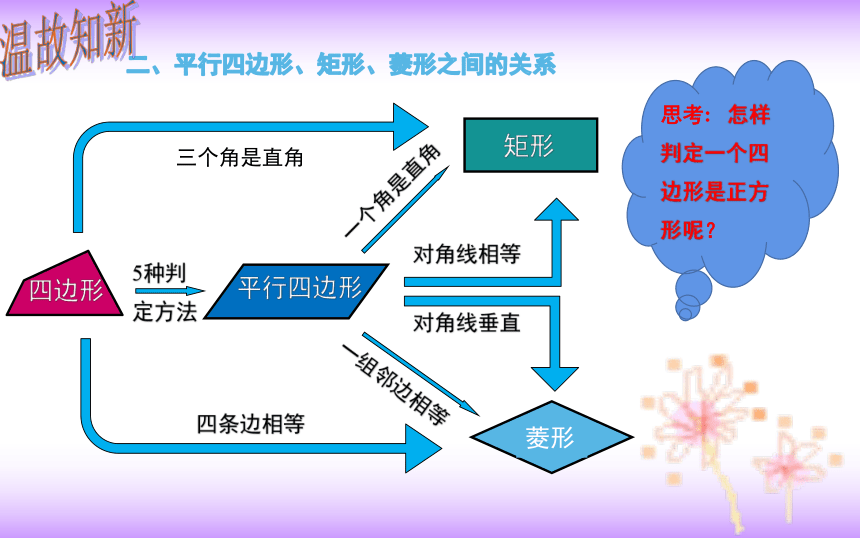
二、平行四边形、矩形、菱形之间的关系
菱形
矩形
平行四边形
四边形
思考:
怎样判定一个四边形是正方形呢?
温故知新
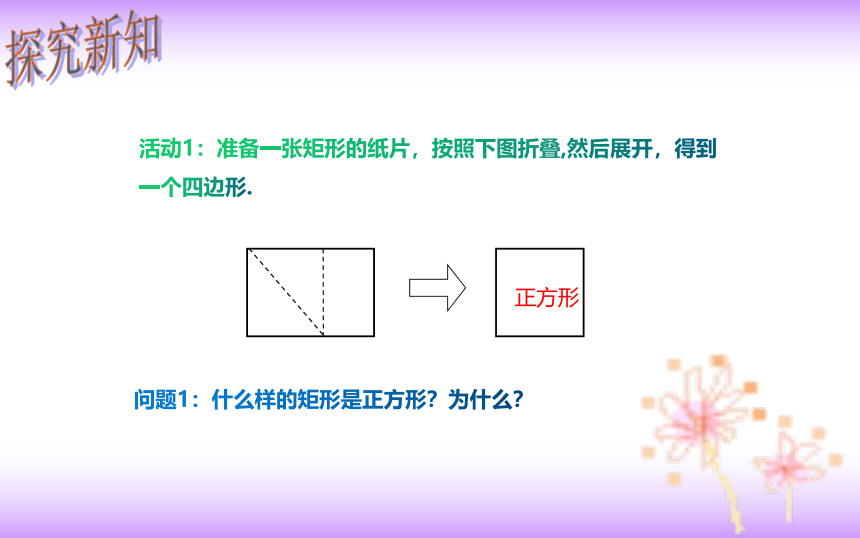
活动1:准备一张矩形的纸片,按照下图折叠,然后展开,得到一个四边形.
问题1:什么样的矩形是正方形?为什么?
正方形
探究新知
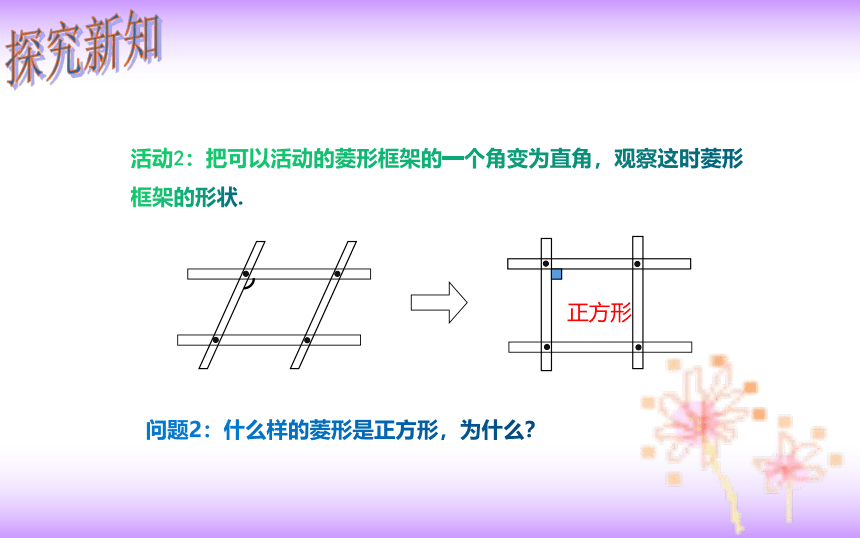
活动2:把可以活动的菱形框架的一个角变为直角,观察这时菱形框架的形状.
问题2:什么样的菱形是正方形,为什么?
正方形
探究新知
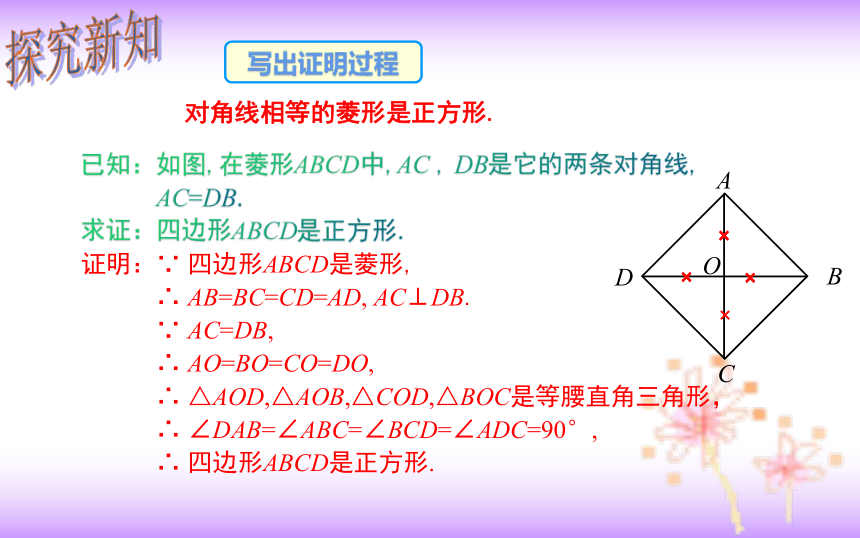
已知:如图,在菱形ABCD中,AC
,
DB是它的两条对角线,
AC=DB.
求证:四边形ABCD是正方形.
证明:∵
四边形ABCD是菱形,
∴
AB=BC=CD=AD,
AC⊥DB.
∵
AC=DB,
∴
AO=BO=CO=DO,
∴
△AOD,△AOB,△COD,△BOC是等腰直角三角形,
∴
∠DAB=∠ABC=∠BCD=∠ADC=90°,
∴
四边形ABCD是正方形.
A
B
C
D
O
对角线相等的菱形是正方形.
写出证明过程
×
×
×
×
×
×
×
×
×
×
探究新知
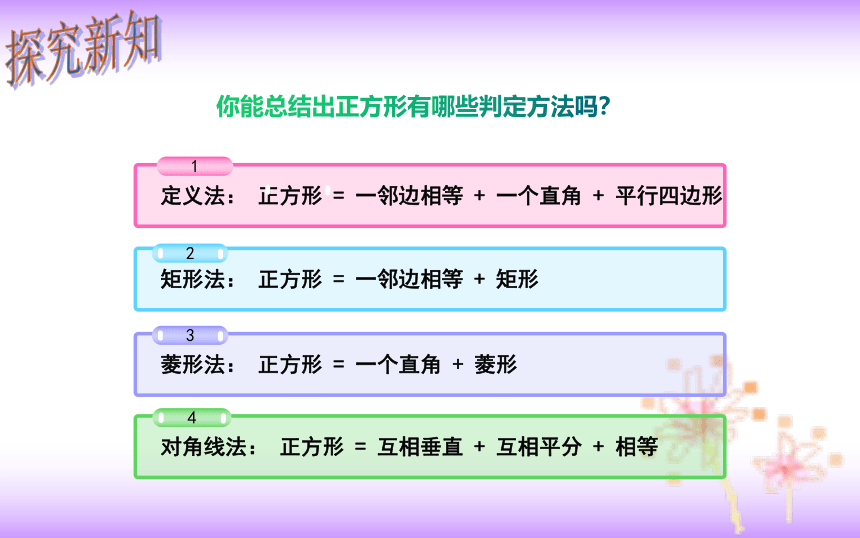
矩形法:
正方形
=
一邻边相等
+
矩形
2
定义法:
正方形
=
一邻边相等
+
一个直角
+
平行四边形
1
菱形法:
正方形
=
一个直角
+
菱形
3
对角线法:
正方形
=
互相垂直
+
互相平分
+
相等
4
你能总结出正方形有哪些判定方法吗?
探究新知
例1
在正方形ABCD中,点E、F、G、H分别在各边上,且AE=BF=CM=DN.四边形EFMN是正方形吗?为什么?
M
N
证明:∵四边形ABCD是正方形,∴AB=BC=CD=DA,∠A=∠B=∠C=∠D=90°,
∵AE=BF=CM=DN,∴AN=BE=CF=DM.
在△AEN、△BFE、△CMF、△DNM中,
AE=BF=CM=DN
∠A=∠B=∠C=∠D
AN=BE=CF=DM
∴△AEN≌△BFE≌△CMF≌△DNM
∴EN=FE=MF=NM,∠ANE=∠BEF
∴四边形EFMN是菱形,
∠NEF=180°-(∠AEN+∠BEF)
=180°-(∠AEN+∠ANE)=180°-90°=90°.
∴四边形EFMN是正方形
.
例题讲解
例2.如图,点O是线段AB上的一点,OA=OC,OD平分∠AOC交AC于点D,OF平分∠COB.CF⊥OF于点F.若∠AOC=900,求证:四边形CDOF是正方形
证明
:∵OA=OC,OD平分∠AOC
∴OD⊥AC,DC=DA
∴∠CDO=900
∵OD平分∠AOC交AC于点D,OF平分∠COB.
∴∠COD=∠COA,∠COF=∠COB
∵∠COA+∠COB=1800
∴∠DOF=∠COD+∠COF=900
∵CF⊥OF,
∴∠CFO=900
∴∠CFO=∠DOF=∠CDO=900
∴四边形DOFC是矩形
∵∠AOC=900,DC=DA
∴OD=DC=DA
∴矩形DOFC是正方形
例题讲解
1.下列命题正确的是(
)
A.
四个角都相等的四边形是正方形
B.
四条边都相等的四边形是正方形
C.
对角线相等的平行四边形是正方形
D.
对角线互相垂直的矩形是正方形
D
D
2.
如图,已知四边形ABCD是平行四边形,下列结论中不正确的是(
)
A.
当AB=BC时,四边形ABCD是菱形
B.当AC⊥BD时,四边形ABCD是菱形
C.当∠ABC=90°时,四边形ABCD是矩形
D.当AC=BD时,四边形ABCD是正方形
巩固练习
3.
如图,四边形ABCD中,ABC=∠BCD=∠CDA=90°,
请添加一个条件____________________,
可得出该四边形是正方形.
AB=BC(答案不唯一)
4.
已知四边形ABCD是平行四边形,再从①AB=BC,②∠ABC=90°,③AC=BD,
④AC⊥BD四个条件中,选两个作为补充条件后,使得四边形ABCD是正方形,
其中错误的是_________________(只填写序号).
②③或①④
A
B
C
D
O
巩固练习
5.
如图所示,正方形ABCD中,P为BD上一点,PE⊥BC于E,
PF⊥DC于F。试说明:AP=EF
A
B
C
D
P
E
F
解:
连接PC
∵
PE⊥BC
,
PF⊥DC
而四边形ABCD是正方形
∴
∠FCE=90°
∴
四边形PECF是矩形
∴
PC=EF
又∵
四边形BAPC是以BD为轴的轴对称图形
∴
AP=PC
∴
AP=EF
巩固练习
证明:∵
DE⊥AC,DF⊥AB
∴∠DEC=
∠DFC=90°.
又∵
∠C=90
°
∴四边形ADFC是矩形.
过点D作DG⊥AB,垂足为G
∵AD是∠CAB的平分线
DE⊥AC,DG⊥AB
∴
DE=DG
同理:DG=DF
∴ED=DF
∴四边形ADFC是正方形.
6.
如图,在直角三角形中,∠C=90°,∠A、∠B的平分线交于点D.DE⊥AC,DF⊥AB.求证:四边形CEDF为正方形.
A
B
C
D
E
F
G
巩固练习
5种判定方法
三个角是直角
四条边相等
一个角是直角
对角线相等
一组邻边相等
对角线垂直
平行四边形、矩形、菱形、正方形之间的关系
菱形
矩形
平行四边形
四边形
正方形
一组邻边相等
对角线垂直
一个角是直角
对角线相等
一组邻边相等且一内角是直角
对角线互相垂直且相等
课堂小结
布置作业
教科书62页,习题18.2
13题
教科书第60页第3、6题
布置作业
再见
空白演示
单击输入您的封面副标题
18.2.3
正方形的判定
人教
版八年级数学下册
一、复习:什么是正方形?正方形有哪些性质?
A
B
C
D
正方形:有一组邻边相等,并且有一个角是直角的平行四边形.
正方形性质:①四个角都是直角;
②四条边都相等;
③对角线相等且互相垂直平分.
O
温故知新
5种判定方法
三个角是直角
四条边相等
一个角是直角
对角线相等
一组邻边相等
对角线垂直
二、平行四边形、矩形、菱形之间的关系
菱形
矩形
平行四边形
四边形
思考:
怎样判定一个四边形是正方形呢?
温故知新
活动1:准备一张矩形的纸片,按照下图折叠,然后展开,得到一个四边形.
问题1:什么样的矩形是正方形?为什么?
正方形
探究新知
活动2:把可以活动的菱形框架的一个角变为直角,观察这时菱形框架的形状.
问题2:什么样的菱形是正方形,为什么?
正方形
探究新知
已知:如图,在菱形ABCD中,AC
,
DB是它的两条对角线,
AC=DB.
求证:四边形ABCD是正方形.
证明:∵
四边形ABCD是菱形,
∴
AB=BC=CD=AD,
AC⊥DB.
∵
AC=DB,
∴
AO=BO=CO=DO,
∴
△AOD,△AOB,△COD,△BOC是等腰直角三角形,
∴
∠DAB=∠ABC=∠BCD=∠ADC=90°,
∴
四边形ABCD是正方形.
A
B
C
D
O
对角线相等的菱形是正方形.
写出证明过程
×
×
×
×
×
×
×
×
×
×
探究新知
矩形法:
正方形
=
一邻边相等
+
矩形
2
定义法:
正方形
=
一邻边相等
+
一个直角
+
平行四边形
1
菱形法:
正方形
=
一个直角
+
菱形
3
对角线法:
正方形
=
互相垂直
+
互相平分
+
相等
4
你能总结出正方形有哪些判定方法吗?
探究新知
例1
在正方形ABCD中,点E、F、G、H分别在各边上,且AE=BF=CM=DN.四边形EFMN是正方形吗?为什么?
M
N
证明:∵四边形ABCD是正方形,∴AB=BC=CD=DA,∠A=∠B=∠C=∠D=90°,
∵AE=BF=CM=DN,∴AN=BE=CF=DM.
在△AEN、△BFE、△CMF、△DNM中,
AE=BF=CM=DN
∠A=∠B=∠C=∠D
AN=BE=CF=DM
∴△AEN≌△BFE≌△CMF≌△DNM
∴EN=FE=MF=NM,∠ANE=∠BEF
∴四边形EFMN是菱形,
∠NEF=180°-(∠AEN+∠BEF)
=180°-(∠AEN+∠ANE)=180°-90°=90°.
∴四边形EFMN是正方形
.
例题讲解
例2.如图,点O是线段AB上的一点,OA=OC,OD平分∠AOC交AC于点D,OF平分∠COB.CF⊥OF于点F.若∠AOC=900,求证:四边形CDOF是正方形
证明
:∵OA=OC,OD平分∠AOC
∴OD⊥AC,DC=DA
∴∠CDO=900
∵OD平分∠AOC交AC于点D,OF平分∠COB.
∴∠COD=∠COA,∠COF=∠COB
∵∠COA+∠COB=1800
∴∠DOF=∠COD+∠COF=900
∵CF⊥OF,
∴∠CFO=900
∴∠CFO=∠DOF=∠CDO=900
∴四边形DOFC是矩形
∵∠AOC=900,DC=DA
∴OD=DC=DA
∴矩形DOFC是正方形
例题讲解
1.下列命题正确的是(
)
A.
四个角都相等的四边形是正方形
B.
四条边都相等的四边形是正方形
C.
对角线相等的平行四边形是正方形
D.
对角线互相垂直的矩形是正方形
D
D
2.
如图,已知四边形ABCD是平行四边形,下列结论中不正确的是(
)
A.
当AB=BC时,四边形ABCD是菱形
B.当AC⊥BD时,四边形ABCD是菱形
C.当∠ABC=90°时,四边形ABCD是矩形
D.当AC=BD时,四边形ABCD是正方形
巩固练习
3.
如图,四边形ABCD中,ABC=∠BCD=∠CDA=90°,
请添加一个条件____________________,
可得出该四边形是正方形.
AB=BC(答案不唯一)
4.
已知四边形ABCD是平行四边形,再从①AB=BC,②∠ABC=90°,③AC=BD,
④AC⊥BD四个条件中,选两个作为补充条件后,使得四边形ABCD是正方形,
其中错误的是_________________(只填写序号).
②③或①④
A
B
C
D
O
巩固练习
5.
如图所示,正方形ABCD中,P为BD上一点,PE⊥BC于E,
PF⊥DC于F。试说明:AP=EF
A
B
C
D
P
E
F
解:
连接PC
∵
PE⊥BC
,
PF⊥DC
而四边形ABCD是正方形
∴
∠FCE=90°
∴
四边形PECF是矩形
∴
PC=EF
又∵
四边形BAPC是以BD为轴的轴对称图形
∴
AP=PC
∴
AP=EF
巩固练习
证明:∵
DE⊥AC,DF⊥AB
∴∠DEC=
∠DFC=90°.
又∵
∠C=90
°
∴四边形ADFC是矩形.
过点D作DG⊥AB,垂足为G
∵AD是∠CAB的平分线
DE⊥AC,DG⊥AB
∴
DE=DG
同理:DG=DF
∴ED=DF
∴四边形ADFC是正方形.
6.
如图,在直角三角形中,∠C=90°,∠A、∠B的平分线交于点D.DE⊥AC,DF⊥AB.求证:四边形CEDF为正方形.
A
B
C
D
E
F
G
巩固练习
5种判定方法
三个角是直角
四条边相等
一个角是直角
对角线相等
一组邻边相等
对角线垂直
平行四边形、矩形、菱形、正方形之间的关系
菱形
矩形
平行四边形
四边形
正方形
一组邻边相等
对角线垂直
一个角是直角
对角线相等
一组邻边相等且一内角是直角
对角线互相垂直且相等
课堂小结
布置作业
教科书62页,习题18.2
13题
教科书第60页第3、6题
布置作业
再见
