8.5.2直线与平面平行第一课时-【新教材】2020-2021学年人教A版(2019)高中数学必修第二册课件(共16张PPT)
文档属性
| 名称 | 8.5.2直线与平面平行第一课时-【新教材】2020-2021学年人教A版(2019)高中数学必修第二册课件(共16张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 727.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-04-19 23:28:16 | ||
图片预览

文档简介
(共16张PPT)
8.5.2直线与平面平行
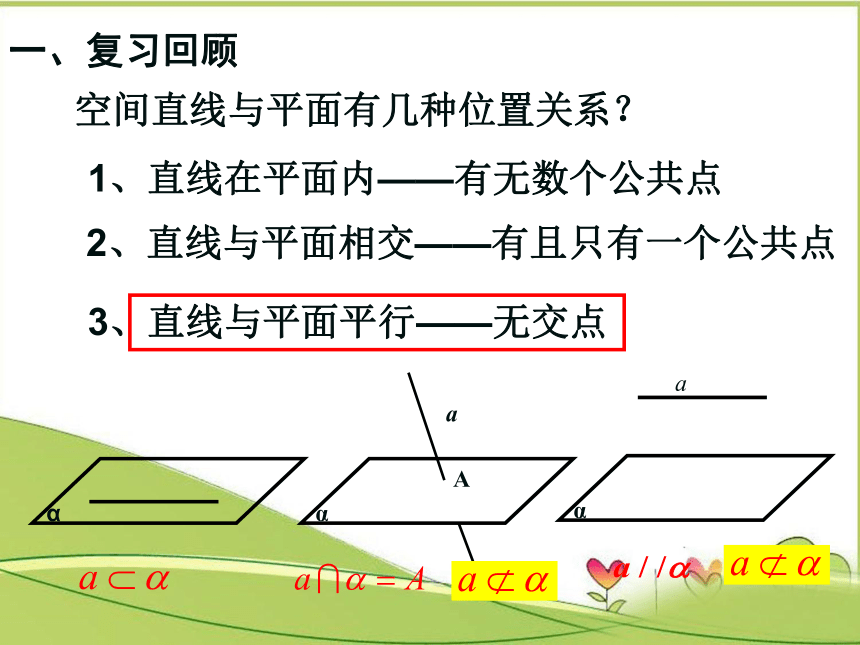
一、复习回顾
空间直线与平面有几种位置关系?
1、直线在平面内——有无数个公共点
2、直线与平面相交——有且只有一个公共点
3、直线与平面平行——无交点
α
α
a
A
α
a
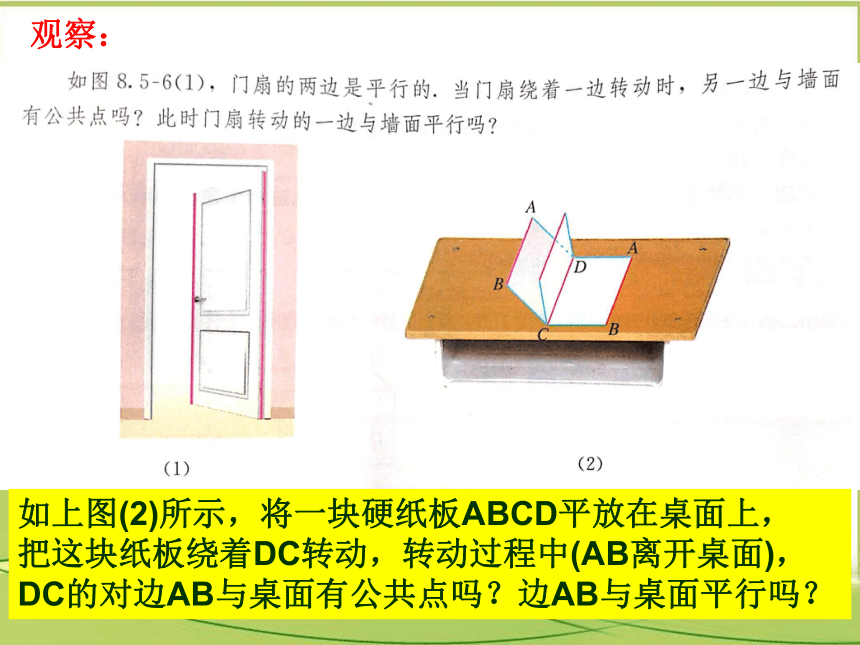
观察:
如上图(2)所示,将一块硬纸板ABCD平放在桌面上,
把这块纸板绕着DC转动,转动过程中(AB离开桌面),
DC的对边AB与桌面有公共点吗?边AB与桌面平行吗?
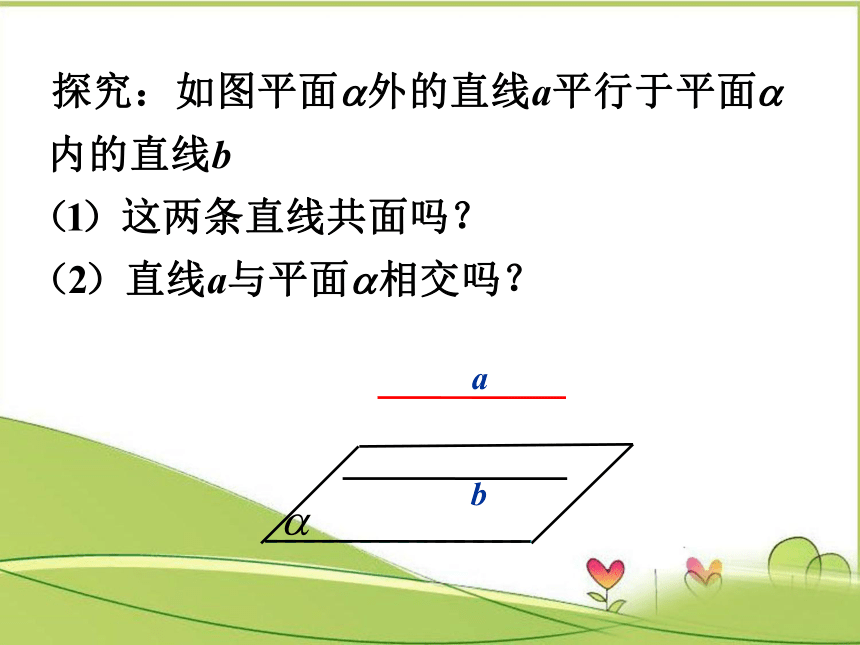
a
b
a
b
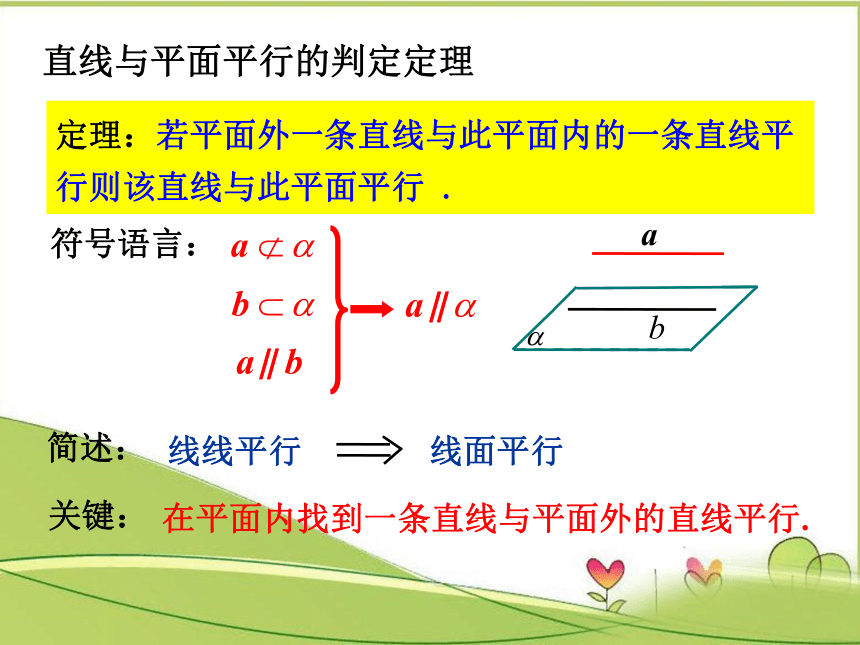
直线与平面平行的判定定理
∥
∥
符号语言:
简述:
线线平行
线面平行
在平面内找到一条直线与平面外的直线平行.
关键:
定理:若平面外一条直线与此平面内的一条直线平行则该直线与此平面平行
.
E
F
A
B
D
C
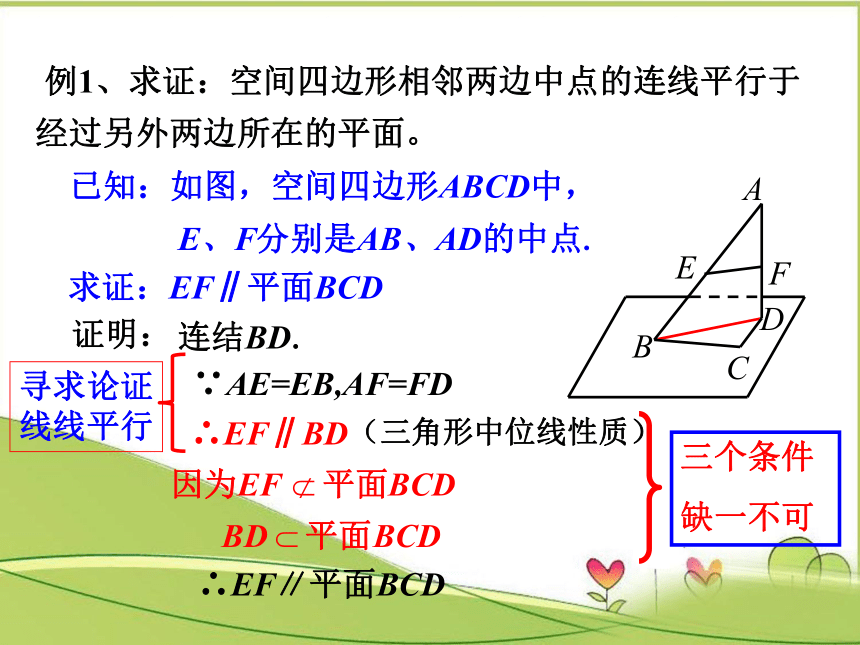
求证:EF∥平面BCD
已知:如图,空间四边形ABCD中,
E、F分别是AB、AD的中点.
证明:
∴EF∥平面BCD
连结BD.
∵AE=EB,AF=FD
∴EF∥BD
(三角形中位线性质)
寻求论证
线线平行
例1、求证:空间四边形相邻两边中点的连线平行于经过另外两边所在的平面。
三个条件
缺一不可
E
F
A
B
D
C
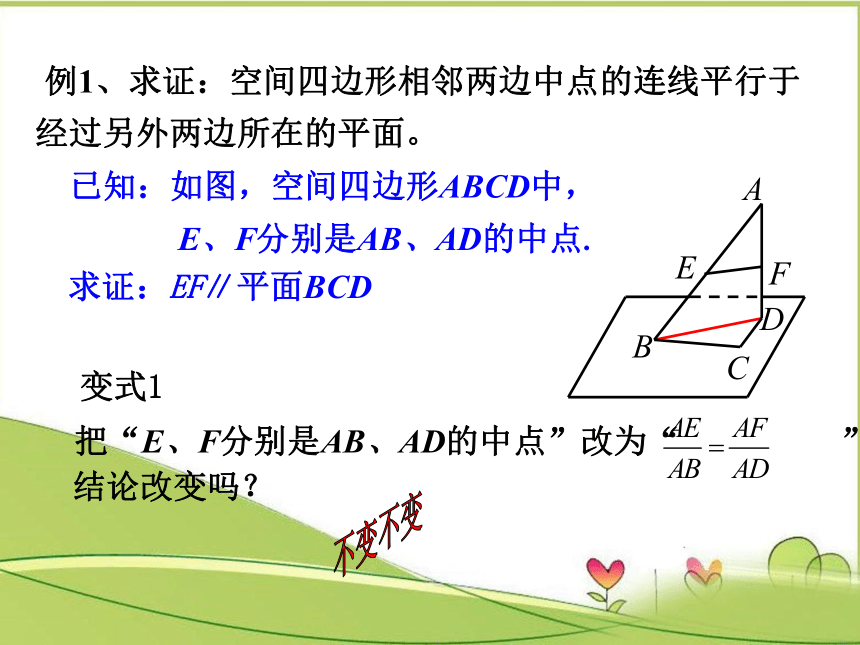
求证:EF∥平面BCD
已知:如图,空间四边形ABCD中,
E、F分别是AB、AD的中点.
把“E、F分别是AB、AD的中点”改为“
”
结论改变吗?
变式1
例1、求证:空间四边形相邻两边中点的连线平行于经过另外两边所在的平面。
A
B
C
D
A1
B1
C1
D1
E
总结判断证明线线平行的一般方法:
4.平行公理
(事实4);
2.
平行四边形的性质;
3.三角形中位线性质;
5.
平行线的判定定理;
1.空间几何体的结构特征;
F
E
F
A
B
D
C
A
E
B
D
C
练习
如图,空间四边形ABCD中,E是AB的中点,试过
CE作一平面平行于BD。
F
S
D
A
B
C
M
O
例2、设S是平行四边形ABCD所在平面外一点,M是SC的中点,求证:SA∥面BMD
例2、设S是平行四边形ABCD所在平面外一点,M是SC的中点,求证:SA∥面BMD
S
D
A
B
C
M
O
1.
填空
课堂练习:
已知:如图在长方体ABCD-A1B1C1D1中,E是AB的中点
(2)
直线AA1与平面BB1C1C的
位置关系是_________;
(1)
直线A1
E与平面BB1C1C的位置关系是________;
A
B
C
D
A1
B1
C1
D1
平行
相交
(3)
直线AC与平面A1B1C1D1的位置关系是_________;
平行
E
(4)
若点F是BC的中点,则直线EF与平面A1B1C1D1的
位置关系是________。
平行
F
A1
B1
C1
D1
A
B
C
D
2、如图在正方体ABCD-A1B1C1D1中,E为DD1的中点,试判断BD1与平面ACE的位置关系.并说明理由.
E
O
课堂练习:课本P138-2
1.判定直线与平面平行的方法:
(1)定义法:直线与平面没有公共点,则线面平行;
符号语言:
∥
∥
2.思想方法
思想:
方法:
空间问题
平面问题
课堂小结
(2)判定定理:(线线平行
线面平行);
线线平行
线面平行
8.5.2直线与平面平行
一、复习回顾
空间直线与平面有几种位置关系?
1、直线在平面内——有无数个公共点
2、直线与平面相交——有且只有一个公共点
3、直线与平面平行——无交点
α
α
a
A
α
a
观察:
如上图(2)所示,将一块硬纸板ABCD平放在桌面上,
把这块纸板绕着DC转动,转动过程中(AB离开桌面),
DC的对边AB与桌面有公共点吗?边AB与桌面平行吗?
a
b
a
b
直线与平面平行的判定定理
∥
∥
符号语言:
简述:
线线平行
线面平行
在平面内找到一条直线与平面外的直线平行.
关键:
定理:若平面外一条直线与此平面内的一条直线平行则该直线与此平面平行
.
E
F
A
B
D
C
求证:EF∥平面BCD
已知:如图,空间四边形ABCD中,
E、F分别是AB、AD的中点.
证明:
∴EF∥平面BCD
连结BD.
∵AE=EB,AF=FD
∴EF∥BD
(三角形中位线性质)
寻求论证
线线平行
例1、求证:空间四边形相邻两边中点的连线平行于经过另外两边所在的平面。
三个条件
缺一不可
E
F
A
B
D
C
求证:EF∥平面BCD
已知:如图,空间四边形ABCD中,
E、F分别是AB、AD的中点.
把“E、F分别是AB、AD的中点”改为“
”
结论改变吗?
变式1
例1、求证:空间四边形相邻两边中点的连线平行于经过另外两边所在的平面。
A
B
C
D
A1
B1
C1
D1
E
总结判断证明线线平行的一般方法:
4.平行公理
(事实4);
2.
平行四边形的性质;
3.三角形中位线性质;
5.
平行线的判定定理;
1.空间几何体的结构特征;
F
E
F
A
B
D
C
A
E
B
D
C
练习
如图,空间四边形ABCD中,E是AB的中点,试过
CE作一平面平行于BD。
F
S
D
A
B
C
M
O
例2、设S是平行四边形ABCD所在平面外一点,M是SC的中点,求证:SA∥面BMD
例2、设S是平行四边形ABCD所在平面外一点,M是SC的中点,求证:SA∥面BMD
S
D
A
B
C
M
O
1.
填空
课堂练习:
已知:如图在长方体ABCD-A1B1C1D1中,E是AB的中点
(2)
直线AA1与平面BB1C1C的
位置关系是_________;
(1)
直线A1
E与平面BB1C1C的位置关系是________;
A
B
C
D
A1
B1
C1
D1
平行
相交
(3)
直线AC与平面A1B1C1D1的位置关系是_________;
平行
E
(4)
若点F是BC的中点,则直线EF与平面A1B1C1D1的
位置关系是________。
平行
F
A1
B1
C1
D1
A
B
C
D
2、如图在正方体ABCD-A1B1C1D1中,E为DD1的中点,试判断BD1与平面ACE的位置关系.并说明理由.
E
O
课堂练习:课本P138-2
1.判定直线与平面平行的方法:
(1)定义法:直线与平面没有公共点,则线面平行;
符号语言:
∥
∥
2.思想方法
思想:
方法:
空间问题
平面问题
课堂小结
(2)判定定理:(线线平行
线面平行);
线线平行
线面平行
同课章节目录
- 第六章 平面向量及其应用
- 6.1 平面向量的概念
- 6.2 平面向量的运算
- 6.3 平面向量基本定理及坐标表示
- 6.4 平面向量的应用
- 第七章 复数
- 7.1 复数的概念
- 7.2 复数的四则运算
- 7.3 * 复数的三角表示
- 第八章 立体几何初步
- 8.1 基本立体图形
- 8.2 立体图形的直观图
- 8.3 简单几何体的表面积与体积
- 8.4 空间点、直线、平面之间的位置关系
- 8.5 空间直线、平面的平行
- 8.6 空间直线、平面的垂直
- 第九章 统计
- 9.1 随机抽样
- 9.2 用样本估计总体
- 9.3 统计分析案例 公司员工
- 第十章 概率
- 10.1 随机事件与概率
- 10.2 事件的相互独立性
- 10.3 频率与概率
