2020-2021学年高二下学期数学人教A版(2019)选择性必修第三册第六章6.3.2二项式系数的性质 课件(共18张PPT)(山东省单县第一中学)
文档属性
| 名称 | 2020-2021学年高二下学期数学人教A版(2019)选择性必修第三册第六章6.3.2二项式系数的性质 课件(共18张PPT)(山东省单县第一中学) |

|
|
| 格式 | pptx | ||
| 文件大小 | 546.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-04-20 00:00:00 | ||
图片预览



文档简介
6.3.2二项式系数的性质
1、二项式定理
展开式
共有 个项.
n+1
2、二项展开式的通项
3、二项式的系数
复习回顾
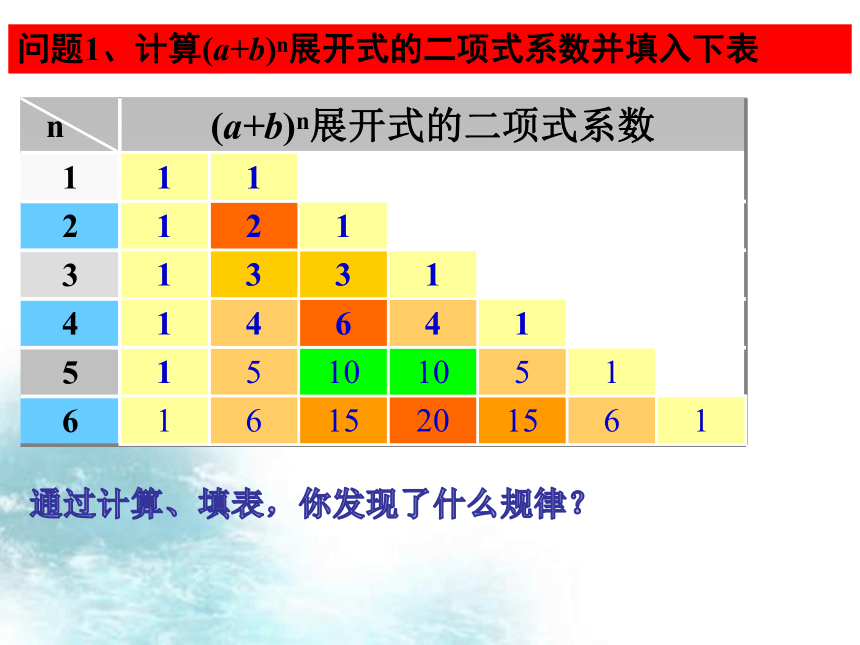
问题1、计算(a+b)n展开式的二项式系数并填入下表
n
(a+b)n展开式的二项式系数
1
2
3
4
5
6
1
6
15
20
15
6
1
1
5
10
10
5
1
1
4
6
4
1
1
3
3
1
1
2
1
1
1
通过计算、填表,你发现了什么规律?
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}(a+b)1
…………………………
1 1
(a+b)2
…………………………
1 2 1
(a+b)3
…………………
1 3 3 1
(a+b)4
…………………
1
4
6
4
1
(a+b)5
…………
1 5 10 10 5 1
(a+b)6
…………
1
6
15
20
15
6
1
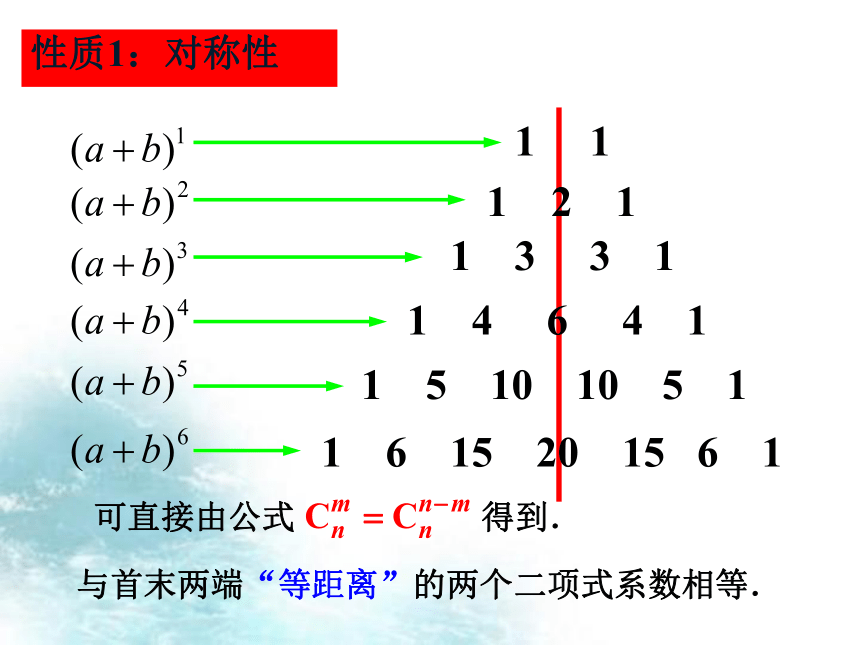
我们可以从中发现,每一行的系数具有对称性.除此之外,还有什么规律呢?
1.在同一行中,每行的两端都是1,与这两个1等距离的项的系数相等;
2.在相邻的两行中,除1以外,每一个数都等于它“肩上”两个数的和.
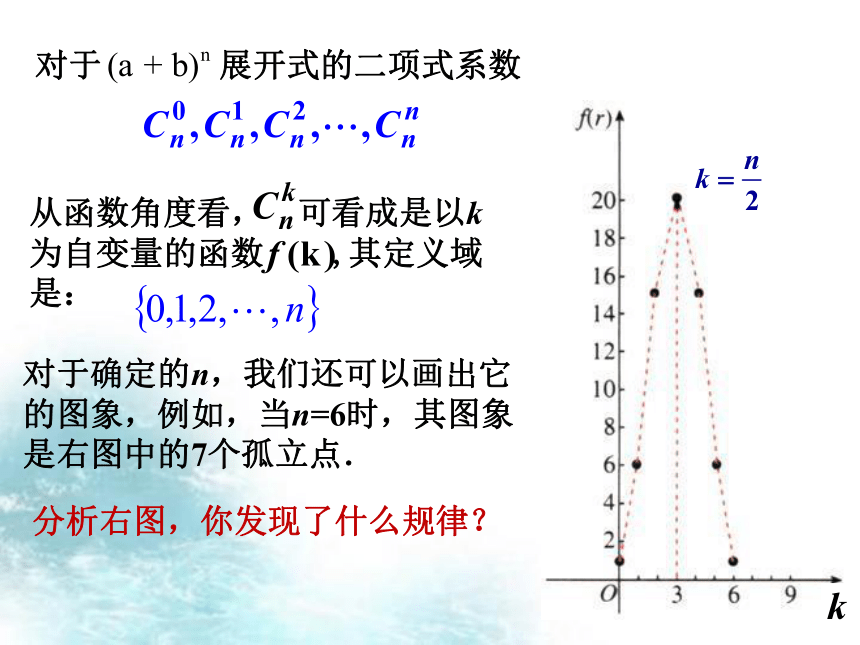
对于 展开式的二项式系数
从函数角度看, 可看成是以k为自变量的函数 ,其定义域是:
对于确定的n,我们还可以画出它
的图象,例如,当n=6时,其图象
是右图中的7个孤立点.
分析右图,你发现了什么规律?
1 4 6 4 1
1 1
1 2 1
1 3 3 1
1 5 10 10 5 1
1 6 15 20 15 6 1
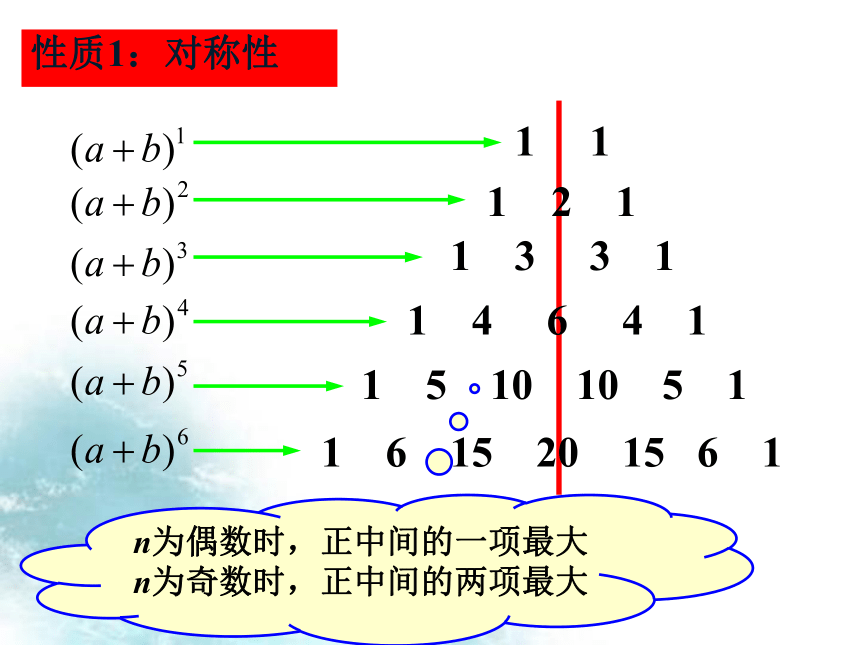
性质1:对称性
与首末两端“等距离”的两个二项式系数相等.
可直接由公式 得到.
n为偶数时,正中间的一项最大
n为奇数时,正中间的两项最大
1 1
1 4 6 4 1
1 2 1
1 3 3 1
1 5 10 10 5 1
1 6 15 20 15 6 1
性质1:对称性
性质2:增减性与最大值
二项式系数是逐渐增大的,
由对称性可知它的后半部分是逐渐减小的,即先增后减,
所以在中间项取得最大值。
所以,当 时,
性质2:增减性与最大值
∵二项展开式共有n+1项,
∴当n为偶数时,正中间一项的二项式系数 最大;
当n为奇数时,中间两项的二项式系数 相等,
且同时取得最大值
1、在(a+b)20展开式中,第五项与第_____项的的二项式
系数相同;
练习:
17
2、已知(1+x)n的展开式中的第4项和第8项的系数相等,求这两项的二项式系数(课本35页T8)
练习:
4、在(a-b)11展开式中,二项式系数最大的是第_____项.
系数最小的是第_____项.
6和7
6
二项式系数与系数的区别
3、
(课本复习参考题6 T1(7))
(赋值法)令a=1,b=1,则
同时由于 ,上式还可以写成:
性质3:各二项式系数的和
例1、求证在(a+b)n的展开式中,奇数项的二项式系数
的和等于偶数项的二项式系数的和.
分析:由(a+b)n的展开式可知,
奇数项的二项式系数之和是
偶数项的二项式系数之和是
由于只是要得到这些系数之和,故可采用赋值法
例题分析
例1、求证在(a+b)n的展开式中,奇数项的二项式系数
的和等于偶数项的二项式系数的和.
证明:
∴不妨令a=1,b=-1,则可得
∴在(a+b)n的展开式中,奇数项的二项式系数的和
等于偶数项的二项式系数的和
例题分析
例2已知(1+2x)n的展开式中的第6项和第7项的系数相等
(1)求展开式中二项式系数最大的项;
(2)求展开式中系数最大的项。
(1)∵ (1+2x)n的展开式有9项
∴二项式系数最大的项是
例题分析
不妨设第m+1项的系数最大,则
解得5≤m≤6
∵m∈{0,1,2,…,8} ∴m=5或m=6
例题分析
(1)二项式系数的三个性质
a 单调性;
b 图象;
c 最值
小 结
与首末两端“等距离”的两个二项式系数相等
先增后减,在中间项取得最大值。
(2) 数学思想:函数思想
课后作业
1、课本34页练习T1、T3、T4
2、习题6.3剩余的题目
1、二项式定理
展开式
共有 个项.
n+1
2、二项展开式的通项
3、二项式的系数
复习回顾
问题1、计算(a+b)n展开式的二项式系数并填入下表
n
(a+b)n展开式的二项式系数
1
2
3
4
5
6
1
6
15
20
15
6
1
1
5
10
10
5
1
1
4
6
4
1
1
3
3
1
1
2
1
1
1
通过计算、填表,你发现了什么规律?
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}(a+b)1
…………………………
1 1
(a+b)2
…………………………
1 2 1
(a+b)3
…………………
1 3 3 1
(a+b)4
…………………
1
4
6
4
1
(a+b)5
…………
1 5 10 10 5 1
(a+b)6
…………
1
6
15
20
15
6
1
我们可以从中发现,每一行的系数具有对称性.除此之外,还有什么规律呢?
1.在同一行中,每行的两端都是1,与这两个1等距离的项的系数相等;
2.在相邻的两行中,除1以外,每一个数都等于它“肩上”两个数的和.
对于 展开式的二项式系数
从函数角度看, 可看成是以k为自变量的函数 ,其定义域是:
对于确定的n,我们还可以画出它
的图象,例如,当n=6时,其图象
是右图中的7个孤立点.
分析右图,你发现了什么规律?
1 4 6 4 1
1 1
1 2 1
1 3 3 1
1 5 10 10 5 1
1 6 15 20 15 6 1
性质1:对称性
与首末两端“等距离”的两个二项式系数相等.
可直接由公式 得到.
n为偶数时,正中间的一项最大
n为奇数时,正中间的两项最大
1 1
1 4 6 4 1
1 2 1
1 3 3 1
1 5 10 10 5 1
1 6 15 20 15 6 1
性质1:对称性
性质2:增减性与最大值
二项式系数是逐渐增大的,
由对称性可知它的后半部分是逐渐减小的,即先增后减,
所以在中间项取得最大值。
所以,当 时,
性质2:增减性与最大值
∵二项展开式共有n+1项,
∴当n为偶数时,正中间一项的二项式系数 最大;
当n为奇数时,中间两项的二项式系数 相等,
且同时取得最大值
1、在(a+b)20展开式中,第五项与第_____项的的二项式
系数相同;
练习:
17
2、已知(1+x)n的展开式中的第4项和第8项的系数相等,求这两项的二项式系数(课本35页T8)
练习:
4、在(a-b)11展开式中,二项式系数最大的是第_____项.
系数最小的是第_____项.
6和7
6
二项式系数与系数的区别
3、
(课本复习参考题6 T1(7))
(赋值法)令a=1,b=1,则
同时由于 ,上式还可以写成:
性质3:各二项式系数的和
例1、求证在(a+b)n的展开式中,奇数项的二项式系数
的和等于偶数项的二项式系数的和.
分析:由(a+b)n的展开式可知,
奇数项的二项式系数之和是
偶数项的二项式系数之和是
由于只是要得到这些系数之和,故可采用赋值法
例题分析
例1、求证在(a+b)n的展开式中,奇数项的二项式系数
的和等于偶数项的二项式系数的和.
证明:
∴不妨令a=1,b=-1,则可得
∴在(a+b)n的展开式中,奇数项的二项式系数的和
等于偶数项的二项式系数的和
例题分析
例2已知(1+2x)n的展开式中的第6项和第7项的系数相等
(1)求展开式中二项式系数最大的项;
(2)求展开式中系数最大的项。
(1)∵ (1+2x)n的展开式有9项
∴二项式系数最大的项是
例题分析
不妨设第m+1项的系数最大,则
解得5≤m≤6
∵m∈{0,1,2,…,8} ∴m=5或m=6
例题分析
(1)二项式系数的三个性质
a 单调性;
b 图象;
c 最值
小 结
与首末两端“等距离”的两个二项式系数相等
先增后减,在中间项取得最大值。
(2) 数学思想:函数思想
课后作业
1、课本34页练习T1、T3、T4
2、习题6.3剩余的题目
