2020-2021学年广东省广州大学附中九年级(下)开学数学试卷(Word版 含解析)
文档属性
| 名称 | 2020-2021学年广东省广州大学附中九年级(下)开学数学试卷(Word版 含解析) |  | |
| 格式 | doc | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-04-20 05:42:24 | ||
图片预览


文档简介
2020-2021学年广东省广州大学附中九年级(下)开学数学试卷
一、选择题(共10小题).
1.下列方程中,没有实数根的是( )
A.x2﹣2x=0 B.x2﹣2x﹣1=0 C.x2﹣2x+1=0 D.x2﹣2x+3=0
2.二次函数y=2(x﹣3)2﹣6( )
A.最小值为﹣6 B.最大值为﹣6 C.最小值为3 D.最大值为3
3.下列选项的汽车标志图案中,是中心对称图形的是( )
A. B.
C. D.
4.下列成语中描述的事件必然发生的是( )
A.水中捞月 B.守株待兔 C.日出东方 D.拔苗助长
5.在反比例函数图象的每一支曲线上,y都随x的增大而减小,则k的取值范围是( )
A.k>3 B.k>0 C.k<3 D.k<0
6.一元二次方程x2+2x+m=0有两个不相等的实数根,则( )
A.m>3 B.m=3 C.m<3 D.m≤3
7.圆的直径是13cm,如果圆心与直线上某一点的距离是6.5cm,那么该直线和圆的位置关系是( )
A.相离 B.相切 C.相交 D.相交或相切
8.已知圆锥的底面半径长为5,侧面展开后得到一个半圆,则该圆锥的母线长为( )
A.2.5 B.5 C.10 D.15
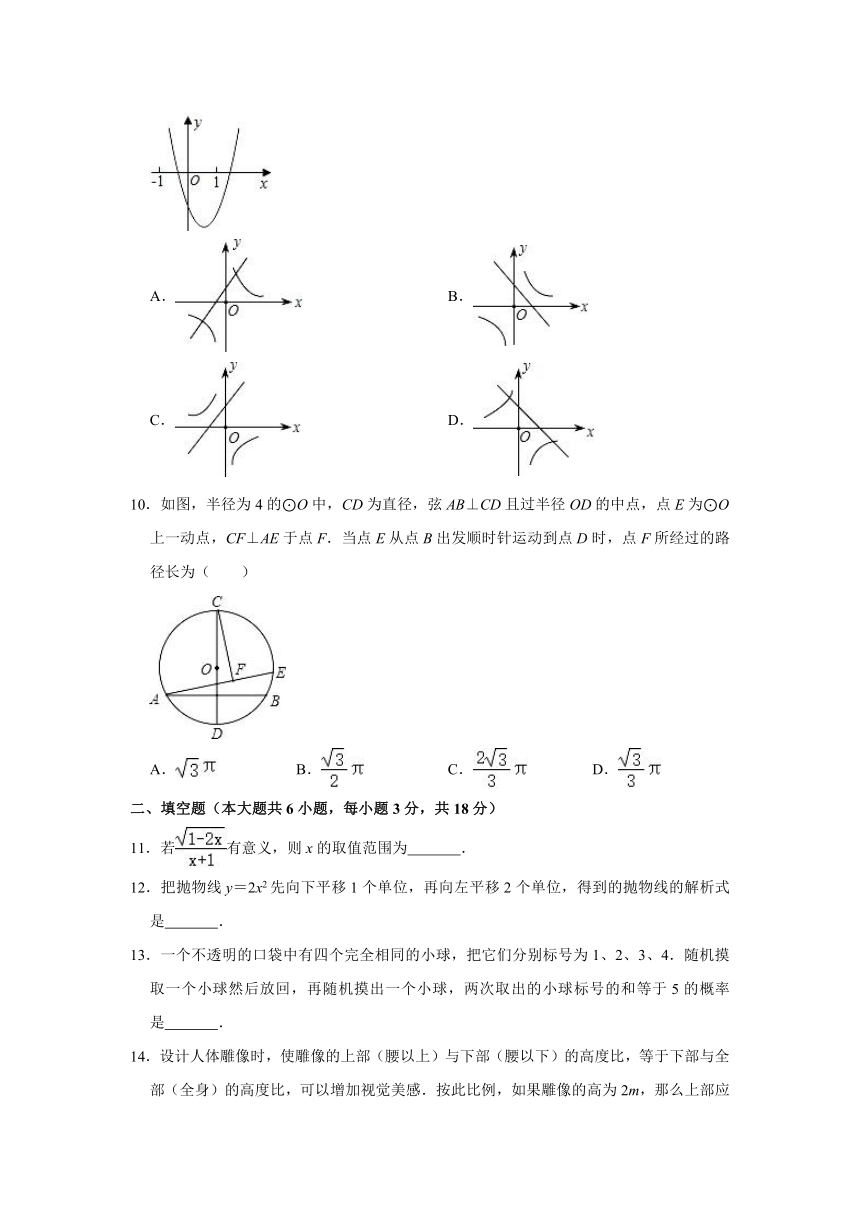
9.二次函数y=ax2+bx+c的图象如图所示,则一次函数y=bx+b2﹣4ac与反比例函数y=在同一坐标系内的图象大致为( )
A. B.
C. D.
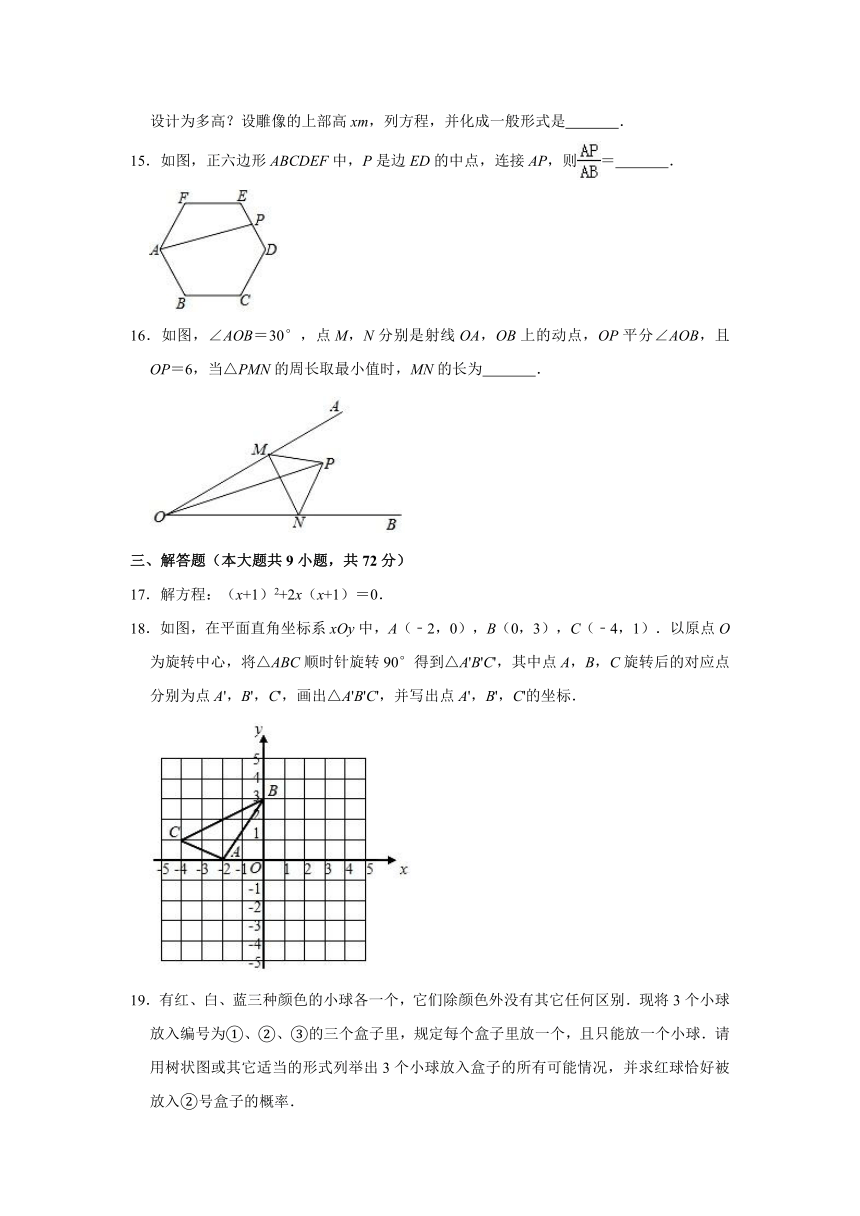
10.如图,半径为4的⊙O中,CD为直径,弦AB⊥CD且过半径OD的中点,点E为⊙O上一动点,CF⊥AE于点F.当点E从点B出发顺时针运动到点D时,点F所经过的路径长为( )
A. B. C. D.
二、填空题(本大题共6小题,每小题3分,共18分)
11.若有意义,则x的取值范围为 .
12.把抛物线y=2x2先向下平移1个单位,再向左平移2个单位,得到的抛物线的解析式是 .
13.一个不透明的口袋中有四个完全相同的小球,把它们分别标号为1、2、3、4.随机摸取一个小球然后放回,再随机摸出一个小球,两次取出的小球标号的和等于5的概率是 .
14.设计人体雕像时,使雕像的上部(腰以上)与下部(腰以下)的高度比,等于下部与全部(全身)的高度比,可以增加视觉美感.按此比例,如果雕像的高为2m,那么上部应设计为多高?设雕像的上部高xm,列方程,并化成一般形式是 .
15.如图,正六边形ABCDEF中,P是边ED的中点,连接AP,则= .
16.如图,∠AOB=30°,点M,N分别是射线OA,OB上的动点,OP平分∠AOB,且OP=6,当△PMN的周长取最小值时,MN的长为 .
三、解答题(本大题共9小题,共72分)
17.解方程:(x+1)2+2x(x+1)=0.
18.如图,在平面直角坐标系xOy中,A(﹣2,0),B(0,3),C(﹣4,1).以原点O为旋转中心,将△ABC顺时针旋转90°得到△A'B'C',其中点A,B,C旋转后的对应点分别为点A',B',C',画出△A'B'C',并写出点A',B',C'的坐标.
19.有红、白、蓝三种颜色的小球各一个,它们除颜色外没有其它任何区别.现将3个小球放入编号为①、②、③的三个盒子里,规定每个盒子里放一个,且只能放一个小球.请用树状图或其它适当的形式列举出3个小球放入盒子的所有可能情况,并求红球恰好被放入②号盒子的概率.
20.如图,已知AD?AC=AB?AE,∠DAE=∠BAC.求证:∠DBA=∠ECA.
21.如图,在⊙O中,∠ACB=∠BDC=60°,AC=2cm.
(1)求∠BAC的度数;(2)求⊙O的周长.
22.投资1万元围成一个矩形菜园(如图),其中一边靠墙,另外三边选用不同材料建造,墙长24m,平行于墙的边的费用为200元/m,垂直于墙的边的费用为150元/m,设平行于墙的边长为xm.
(1)设垂直于墙的一边长为ym,直接写出y与x之间的函数关系式.
(2)若菜园的面积为384m2,求x的值.
(3)求菜园的最大面积.
23.如图,在四边形OABC中,BC∥AO,∠AOC=90°,点A(5,0),B(2,6),点D为AB上一点,且=,双曲线y1=(k1>0)在第一象限的图象经过点D,交BC于点E.
(1)求双曲线的解析式.
(2)一次函数的=k2x+b经过D、E两点,结合图象,写出不等式<k2x+b的解集.
24.如图,二次函数y=x2﹣2x+1图象与一次函数y=kx+b(k≠0)的图象交于A,B两点,点A的坐标为(0,1),点B在第一象限内,点C是二次函数图象的顶点,点M是一次函数y=kx+b(k≠0)的图象与x轴的交点,过点B作x轴的垂线,垂足为N,且S△AMO:S四边形AONB=1:48.
(1)求直线AB和直线BC的解析式.
(2)点P是线段AB上一点,点D是线段BC上一点,PD∥x轴,射线PD与抛物线交于点G,过点P作PE⊥x轴于点E,PF⊥BC于点F,当PF与PE的乘积最大时,在线段AB上找一点H(不与点A,点B重合),使GH+BH的值最小,求点H的坐标和GH+BH的最小值.
25.如图,⊙O的直径AB为10cm,弦AC为6cm,∠ACB的平分线交⊙O于点D.
(1)求AD的长;
(2)试探究CA、CB、CD之间的等量关系,并证明你的结论;
(3)连接OD,P为半圆ADB上任意一点,过P点作PE⊥OD于点E,设△OPE的内心为M,当点P在半圆上从点B运动到点A时,求内心M所经过的路径长.
参考答案
一、选择题(本大题共10小题,每小题3分,共30分)
1.下列方程中,没有实数根的是( )
A.x2﹣2x=0 B.x2﹣2x﹣1=0 C.x2﹣2x+1=0 D.x2﹣2x+3=0
解:A.此方程根的判别式△=(﹣2)2﹣4×1×0=4>0,有两个不相等的实数根,不符合题意;
B.此方程根的判别式△=(﹣2)2﹣4×1×(﹣1)=8>0,有两个不相等的实数根,不符合题意;
C.此方程根的判别式△=(﹣2)2﹣4×1×1=0,有两个相等的实数根,不符合题意;
D.此方程根的判别式△=(﹣2)2﹣4×1×3=﹣8<0,没有实数根,符合题意;
故选:D.
2.二次函数y=2(x﹣3)2﹣6( )
A.最小值为﹣6 B.最大值为﹣6 C.最小值为3 D.最大值为3
解:∵a=2>0,
∴二次函数有最小值为﹣6.
故选:A.
3.下列选项的汽车标志图案中,是中心对称图形的是( )
A. B.
C. D.
解:A、不是中心对称图形,故此选项不合题意;
B、是中心对称图形,故此选项符合题意;
C、不是中心对称图形,故此选项不合题意;
D、不是中心对称图形,故此选项不合题意;
故选:B.
4.下列成语中描述的事件必然发生的是( )
A.水中捞月 B.守株待兔 C.日出东方 D.拔苗助长
解:A、水中捞月,是不可能事件,故本选项不符合题意;
B、守株待兔,是随机事件,故本选项不符合题意;
C、日出东方,是必然事件,故本选项符合题意;
D、拔苗助长,是不可能事件,故本选项不符合题意;
故选:C.
5.在反比例函数图象的每一支曲线上,y都随x的增大而减小,则k的取值范围是( )
A.k>3 B.k>0 C.k<3 D.k<0
解:在图象的每一支曲线上,y都随x的增大而减小,根据反比例函数的性质,
得k﹣3>0,
k>3.
故选:A.
6.一元二次方程x2+2x+m=0有两个不相等的实数根,则( )
A.m>3 B.m=3 C.m<3 D.m≤3
解:∵一元二次方程x2+2x+m=0有两个不相等的实数根,
∴△=(2)2﹣4m>0,
解得:m<3.
故选:C.
7.圆的直径是13cm,如果圆心与直线上某一点的距离是6.5cm,那么该直线和圆的位置关系是( )
A.相离 B.相切 C.相交 D.相交或相切
解:∵圆的直径为13 cm,
∴圆的半径为6.5 cm,
∵圆心与直线上某一点的距离是6.5cm,
∴圆的半径≥圆心到直线的距离,
∴直线于圆相切或相交,
故选:D.
8.已知圆锥的底面半径长为5,侧面展开后得到一个半圆,则该圆锥的母线长为( )
A.2.5 B.5 C.10 D.15
解:设母线长为x,根据题意得
2πx÷2=2π×5,
解得x=10.
故选:C.
9.二次函数y=ax2+bx+c的图象如图所示,则一次函数y=bx+b2﹣4ac与反比例函数y=在同一坐标系内的图象大致为( )
A. B.
C. D.
解:由抛物线的图象可知,横坐标为1的点,即(1,a+b+c)在第四象限,因此a+b+c<0;
∴双曲线的图象在第二、四象限;
由于抛物线开口向上,所以a>0;
对称轴x=>0,所以b<0;
抛物线与x轴有两个交点,故b2﹣4ac>0;
∴直线y=bx+b2﹣4ac经过第一、二、四象限.
故选:D.
10.如图,半径为4的⊙O中,CD为直径,弦AB⊥CD且过半径OD的中点,点E为⊙O上一动点,CF⊥AE于点F.当点E从点B出发顺时针运动到点D时,点F所经过的路径长为( )
A. B. C. D.
解:连接AC,AO,
∵AB⊥CD,
∴G为AB的中点,即AG=BG=AB,
∵⊙O的半径为4,弦AB⊥CD且过半径OD的中点,
∴OG=2,
∴在Rt△AOG中,根据勾股定理得:AG==2,
又∵CG=CO+GO=4+2=6,
∴在Rt△AGC中,根据勾股定理得:AC==4,
∵CF⊥AE,
∴△ACF始终是直角三角形,点F的运动轨迹为以AC为直径的半圆,
当E位于点B时,CG⊥AE,此时F与G重合;当E位于D时,CA⊥AE,此时F与A重合,
∴当点E从点B出发顺时针运动到点D时,点F所经过的路径长,
在Rt△ACG中,tan∠ACG==,
∴∠ACG=30°,
∴所对圆心角的度数为60°,
∵直径AC=4,
∴的长为=π,
则当点E从点B出发顺时针运动到点D时,点F所经过的路径长为π.
故选:C.
二、填空题(本大题共6小题,每小题3分,共18分)
11.若有意义,则x的取值范围为 x≤且x≠﹣1 .
解:由题意得:1﹣2x≥0,且x+1≠0,
解得:x≤且x≠﹣1,
故答案为:x≤且x≠﹣1.
12.把抛物线y=2x2先向下平移1个单位,再向左平移2个单位,得到的抛物线的解析式是 y=2(x+2)2﹣1 .
解:由“上加下减”的原则可知,二次函数y=2x2的图象向下平移1个单位得到y=2x2﹣1,
由“左加右减”的原则可知,将二次函数y=2x2﹣1的图象向左平移2个单位可得到函数y=2(x+2)2﹣1,
故答案是:y=2(x+2)2﹣1.
13.一个不透明的口袋中有四个完全相同的小球,把它们分别标号为1、2、3、4.随机摸取一个小球然后放回,再随机摸出一个小球,两次取出的小球标号的和等于5的概率是 .
解:画树状图如下:
随机地摸出一个小球,然后放回,再随机地摸出一个小球,共有16种等可能的结果数,其中两次摸出的小球标号的和等于5的占4种,
所有两次摸出的小球标号的和等于5的概率为=,
故答案为:.
14.设计人体雕像时,使雕像的上部(腰以上)与下部(腰以下)的高度比,等于下部与全部(全身)的高度比,可以增加视觉美感.按此比例,如果雕像的高为2m,那么上部应设计为多高?设雕像的上部高xm,列方程,并化成一般形式是 x2﹣6x+4=0 .
解:设雕像的上部高x m,则题意得:
,
整理得:x2﹣6x+4=0,
故答案为:x2﹣6x+4=0
15.如图,正六边形ABCDEF中,P是边ED的中点,连接AP,则= .
解:连接AE,过点F作FH⊥AE,
∵六边形ABCDEF是正六边形,
∴AB=BC=CD=DE=EF=a,
∠AFE=∠DEF=120°,
∴∠FAE=∠FEA=30°,
∴∠AEP=90°,
∴FH=,
∴AH=,AE=,
∵P是ED的中点,
∴EP=,
∴AP=.
∴=
16.如图,∠AOB=30°,点M,N分别是射线OA,OB上的动点,OP平分∠AOB,且OP=6,当△PMN的周长取最小值时,MN的长为 12﹣18 .
解:设点P关于OA的对称点为C,关于OB的对称点为D,连接OC,OD,CD,CD分别交OA、OB于点M'、N',连接PM'、PN',如图所示:
∵点P关于OA的对称点为C,关于OB的对称点为D,
∴PM'=CM',OP=OC,∠COA=∠POA;PN'=DN',OP=OD,∠DOB=∠POB.
∴OC=OD=OP=6,
∵∠AOB=30°,
∴∠COD=∠COA+∠AOP+∠POB+∠BOD
=2∠AOP+2∠POB
=2∠AOB
=60°,
∴△COD是等边三角形,
∴CD=OC=OD=6,
∵OP平分∠AOB,
∴∠POC=∠POD,
∴OP⊥CD,
∴OQ=6sin60°=6×=3,
∴PQ=6﹣3,
设M'Q=x,则PM'=CM'=3﹣x,
∴(3﹣x)2﹣x2=,
解得x=6﹣9.
∴M'N'=2x=12﹣18.
故答案为:12﹣18.
三、解答题(本大题共9小题,共72分)
17.解方程:(x+1)2+2x(x+1)=0.
解:∵(x+1)2+2x(x+1)=0,
∴(x+1)(3x+1)=0,
则x+1=0或3x+1=0,
解得x1=﹣1,x2=﹣.
18.如图,在平面直角坐标系xOy中,A(﹣2,0),B(0,3),C(﹣4,1).以原点O为旋转中心,将△ABC顺时针旋转90°得到△A'B'C',其中点A,B,C旋转后的对应点分别为点A',B',C',画出△A'B'C',并写出点A',B',C'的坐标.
解:如图,△A'B'C'为所作,点A',B',C'的坐标分别为(0,2),(3,0),(1,4).
19.有红、白、蓝三种颜色的小球各一个,它们除颜色外没有其它任何区别.现将3个小球放入编号为①、②、③的三个盒子里,规定每个盒子里放一个,且只能放一个小球.请用树状图或其它适当的形式列举出3个小球放入盒子的所有可能情况,并求红球恰好被放入②号盒子的概率.
解:画树状图如下,
由树状图知,共有6种等可能结果,其中红球恰好被放入②号盒子的有2种结果,
∴红球恰好被放入②号盒子的概率为=.
20.如图,已知AD?AC=AB?AE,∠DAE=∠BAC.求证:∠DBA=∠ECA.
【解答】证明:∵AD?AC=AB?AE,
∴=,
∴∠DAE=∠BAC,
∴∠DAE﹣∠BAE=∠BAC﹣∠BAE,
即∠DAB=∠EAC,
∴△ADB∽△AEC,
∴∠DBA=∠ECA.
21.如图,在⊙O中,∠ACB=∠BDC=60°,AC=2cm.
(1)求∠BAC的度数;(2)求⊙O的周长.
解:(1)∠BAC=∠BDC=60°(同弧所对的圆周角相等);
(2)∠ABC=180°﹣∠BAC﹣∠ACB=60°,
∴△ABC是等边三角形,
作OE⊥AC于点E,连接OA,则OA平分∠BAC,
∴∠OAE=30°,
∴OA==2cm,
所以⊙O的周长=2π×2=4πcm.
22.投资1万元围成一个矩形菜园(如图),其中一边靠墙,另外三边选用不同材料建造,墙长24m,平行于墙的边的费用为200元/m,垂直于墙的边的费用为150元/m,设平行于墙的边长为xm.
(1)设垂直于墙的一边长为ym,直接写出y与x之间的函数关系式.
(2)若菜园的面积为384m2,求x的值.
(3)求菜园的最大面积.
解:(1)根据题意知,y==﹣x+(0<x≤24);
(2)根据题意,得:(﹣x+)x=384,
解得:x=18或x=32,
∵墙的长度为24m,
∴x=18;
(3)设菜园的面积是S,
则S=(=﹣x+)x
=﹣x2+x
=﹣(x﹣25)2+,
∵﹣<0,
∴当x<25时,S随x的增大而增大,
∵x≤24,
∴当x=24时,S取得最大值,最大值为416,
答:菜园的最大面积为416m2.
23.如图,在四边形OABC中,BC∥AO,∠AOC=90°,点A(5,0),B(2,6),点D为AB上一点,且=,双曲线y1=(k1>0)在第一象限的图象经过点D,交BC于点E.
(1)求双曲线的解析式.
(2)一次函数的=k2x+b经过D、E两点,结合图象,写出不等式<k2x+b的解集.
解:(1)作BM⊥x轴于M,作DN⊥x轴于N,如图,
点A,B的坐标分别为(5,0),(2,6),
∴BC=OM=2,BM=OC=6,AM=3,
∵DN∥BM,
∴△AND∽△ABM,
∴,即,
∴DN=2,AN=1,
∴ON=OA﹣AN=4,
∴D点坐标为(4,2),
把D(4,2)代入y=得k1=2×4=8,
∵反比例函数解析式为y=;
(2)将y=6入y=中,得:x=,
故E(,6),
由图象可知,不等式<k2x+b的解集为<x<6.
24.如图,二次函数y=x2﹣2x+1图象与一次函数y=kx+b(k≠0)的图象交于A,B两点,点A的坐标为(0,1),点B在第一象限内,点C是二次函数图象的顶点,点M是一次函数y=kx+b(k≠0)的图象与x轴的交点,过点B作x轴的垂线,垂足为N,且S△AMO:S四边形AONB=1:48.
(1)求直线AB和直线BC的解析式.
(2)点P是线段AB上一点,点D是线段BC上一点,PD∥x轴,射线PD与抛物线交于点G,过点P作PE⊥x轴于点E,PF⊥BC于点F,当PF与PE的乘积最大时,在线段AB上找一点H(不与点A,点B重合),使GH+BH的值最小,求点H的坐标和GH+BH的最小值.
解:(1)∵BN⊥x轴,
∴BN∥OA,
∴△MAO∽△MBN,
∵S△AMO:S四边形AONB=1:48,即S△AMO:S△MNB=1:49,
∴BN=7OA=7,
即yB=7,令y=x2﹣2x+1=7,解得x=6(不合题意的值已舍去),
故点B的坐标为(6,7),
设直线AB的表达式为y=kx+b,则,解得,
故直线AB的表达式为y=x+1,
由点B、C的坐标,同理可得,直线BC的表达式为y=2x﹣5;
(2)设点P的坐标为(m,m+1),
当y=m+1=2x﹣5时,解得x=3+m,故点D的坐标为(3+m,m+1),
则PD=3+m﹣m=3﹣m,PE=m+1,
∵∠PDF为定值,故PD:PF为定值,
故PD×PE最大时PF×PE也最大,
则PD×PE=(3﹣m)(m+1)=﹣m2+m+3,
∴当m=时,PD×PE最大,
此时,点P的坐标为(,),
令y=x2﹣2x+1=,解得x=5(不合题意的值已舍去),
故点G的坐标为(5,);
过点H作HN∥y轴交过点B与x轴的平行线于点N,连接HG,
由直线AB的表达式知,直线AB与x轴的夹角为45°,则∠NBH=45°,
故NH=BH,
故GH+BH=GH+NH,
故当G、N、H三点共线时,GH+BH取得最小值.
当x=5时,y=x+1=6,故点H的坐标为(5,6);
GH+BH的最小值=yB﹣yG=7﹣=.
25.如图,⊙O的直径AB为10cm,弦AC为6cm,∠ACB的平分线交⊙O于点D.
(1)求AD的长;
(2)试探究CA、CB、CD之间的等量关系,并证明你的结论;
(3)连接OD,P为半圆ADB上任意一点,过P点作PE⊥OD于点E,设△OPE的内心为M,当点P在半圆上从点B运动到点A时,求内心M所经过的路径长.
解:(1)∵AB是⊙O的直径,
∴∠ACB=∠ADB=90°,
∵∠ACB的平分线交⊙O于D,
∴∠ACD=∠BCD=45°,
∴=,
∴AD=BD,
∴AD2+BD2=AB2,
∴AD=BD=AB=×10=5;
(2)CA+CB=CD.
证明如下:延长CA到F,使AF=CB,连接DF,
∵∠CBD+∠CAD=180°,∠FAD+∠CAD=180°,
∴∠CBD=∠FAD,
在△ADF和△BDC中,
,
∴△ADF≌△BDC(SAS),
∴CD=FD,∠CDB=∠FDA,
∴∠CDF=∠ADB=90°,△CDF为等腰直角三角形,
∴CA+CB=CF=CD.
(3)连接OM,PM,
∵PE⊥OD,
∴∠PEO=90°,
∵点M为△OPE的内心,
∴∠OMP=135°,
在△OMD和△OMP中,
,
∴△OMD≌△OMP(SAS),
∴∠OMD=∠OMP=135°,
∴点M在以OD为弦,并且所对的圆周角为135°的两段劣弧上(分OD左右两种情况):
设弧OMD所在圆的圆心为O',
∵∠OMD=135°,
∴∠OO'D=90°,
∴O'O=OD=,
∴的长为=π,
∴点M的路径长为π.
一、选择题(共10小题).
1.下列方程中,没有实数根的是( )
A.x2﹣2x=0 B.x2﹣2x﹣1=0 C.x2﹣2x+1=0 D.x2﹣2x+3=0
2.二次函数y=2(x﹣3)2﹣6( )
A.最小值为﹣6 B.最大值为﹣6 C.最小值为3 D.最大值为3
3.下列选项的汽车标志图案中,是中心对称图形的是( )
A. B.
C. D.
4.下列成语中描述的事件必然发生的是( )
A.水中捞月 B.守株待兔 C.日出东方 D.拔苗助长
5.在反比例函数图象的每一支曲线上,y都随x的增大而减小,则k的取值范围是( )
A.k>3 B.k>0 C.k<3 D.k<0
6.一元二次方程x2+2x+m=0有两个不相等的实数根,则( )
A.m>3 B.m=3 C.m<3 D.m≤3
7.圆的直径是13cm,如果圆心与直线上某一点的距离是6.5cm,那么该直线和圆的位置关系是( )
A.相离 B.相切 C.相交 D.相交或相切
8.已知圆锥的底面半径长为5,侧面展开后得到一个半圆,则该圆锥的母线长为( )
A.2.5 B.5 C.10 D.15
9.二次函数y=ax2+bx+c的图象如图所示,则一次函数y=bx+b2﹣4ac与反比例函数y=在同一坐标系内的图象大致为( )
A. B.
C. D.
10.如图,半径为4的⊙O中,CD为直径,弦AB⊥CD且过半径OD的中点,点E为⊙O上一动点,CF⊥AE于点F.当点E从点B出发顺时针运动到点D时,点F所经过的路径长为( )
A. B. C. D.
二、填空题(本大题共6小题,每小题3分,共18分)
11.若有意义,则x的取值范围为 .
12.把抛物线y=2x2先向下平移1个单位,再向左平移2个单位,得到的抛物线的解析式是 .
13.一个不透明的口袋中有四个完全相同的小球,把它们分别标号为1、2、3、4.随机摸取一个小球然后放回,再随机摸出一个小球,两次取出的小球标号的和等于5的概率是 .
14.设计人体雕像时,使雕像的上部(腰以上)与下部(腰以下)的高度比,等于下部与全部(全身)的高度比,可以增加视觉美感.按此比例,如果雕像的高为2m,那么上部应设计为多高?设雕像的上部高xm,列方程,并化成一般形式是 .
15.如图,正六边形ABCDEF中,P是边ED的中点,连接AP,则= .
16.如图,∠AOB=30°,点M,N分别是射线OA,OB上的动点,OP平分∠AOB,且OP=6,当△PMN的周长取最小值时,MN的长为 .
三、解答题(本大题共9小题,共72分)
17.解方程:(x+1)2+2x(x+1)=0.
18.如图,在平面直角坐标系xOy中,A(﹣2,0),B(0,3),C(﹣4,1).以原点O为旋转中心,将△ABC顺时针旋转90°得到△A'B'C',其中点A,B,C旋转后的对应点分别为点A',B',C',画出△A'B'C',并写出点A',B',C'的坐标.
19.有红、白、蓝三种颜色的小球各一个,它们除颜色外没有其它任何区别.现将3个小球放入编号为①、②、③的三个盒子里,规定每个盒子里放一个,且只能放一个小球.请用树状图或其它适当的形式列举出3个小球放入盒子的所有可能情况,并求红球恰好被放入②号盒子的概率.
20.如图,已知AD?AC=AB?AE,∠DAE=∠BAC.求证:∠DBA=∠ECA.
21.如图,在⊙O中,∠ACB=∠BDC=60°,AC=2cm.
(1)求∠BAC的度数;(2)求⊙O的周长.
22.投资1万元围成一个矩形菜园(如图),其中一边靠墙,另外三边选用不同材料建造,墙长24m,平行于墙的边的费用为200元/m,垂直于墙的边的费用为150元/m,设平行于墙的边长为xm.
(1)设垂直于墙的一边长为ym,直接写出y与x之间的函数关系式.
(2)若菜园的面积为384m2,求x的值.
(3)求菜园的最大面积.
23.如图,在四边形OABC中,BC∥AO,∠AOC=90°,点A(5,0),B(2,6),点D为AB上一点,且=,双曲线y1=(k1>0)在第一象限的图象经过点D,交BC于点E.
(1)求双曲线的解析式.
(2)一次函数的=k2x+b经过D、E两点,结合图象,写出不等式<k2x+b的解集.
24.如图,二次函数y=x2﹣2x+1图象与一次函数y=kx+b(k≠0)的图象交于A,B两点,点A的坐标为(0,1),点B在第一象限内,点C是二次函数图象的顶点,点M是一次函数y=kx+b(k≠0)的图象与x轴的交点,过点B作x轴的垂线,垂足为N,且S△AMO:S四边形AONB=1:48.
(1)求直线AB和直线BC的解析式.
(2)点P是线段AB上一点,点D是线段BC上一点,PD∥x轴,射线PD与抛物线交于点G,过点P作PE⊥x轴于点E,PF⊥BC于点F,当PF与PE的乘积最大时,在线段AB上找一点H(不与点A,点B重合),使GH+BH的值最小,求点H的坐标和GH+BH的最小值.
25.如图,⊙O的直径AB为10cm,弦AC为6cm,∠ACB的平分线交⊙O于点D.
(1)求AD的长;
(2)试探究CA、CB、CD之间的等量关系,并证明你的结论;
(3)连接OD,P为半圆ADB上任意一点,过P点作PE⊥OD于点E,设△OPE的内心为M,当点P在半圆上从点B运动到点A时,求内心M所经过的路径长.
参考答案
一、选择题(本大题共10小题,每小题3分,共30分)
1.下列方程中,没有实数根的是( )
A.x2﹣2x=0 B.x2﹣2x﹣1=0 C.x2﹣2x+1=0 D.x2﹣2x+3=0
解:A.此方程根的判别式△=(﹣2)2﹣4×1×0=4>0,有两个不相等的实数根,不符合题意;
B.此方程根的判别式△=(﹣2)2﹣4×1×(﹣1)=8>0,有两个不相等的实数根,不符合题意;
C.此方程根的判别式△=(﹣2)2﹣4×1×1=0,有两个相等的实数根,不符合题意;
D.此方程根的判别式△=(﹣2)2﹣4×1×3=﹣8<0,没有实数根,符合题意;
故选:D.
2.二次函数y=2(x﹣3)2﹣6( )
A.最小值为﹣6 B.最大值为﹣6 C.最小值为3 D.最大值为3
解:∵a=2>0,
∴二次函数有最小值为﹣6.
故选:A.
3.下列选项的汽车标志图案中,是中心对称图形的是( )
A. B.
C. D.
解:A、不是中心对称图形,故此选项不合题意;
B、是中心对称图形,故此选项符合题意;
C、不是中心对称图形,故此选项不合题意;
D、不是中心对称图形,故此选项不合题意;
故选:B.
4.下列成语中描述的事件必然发生的是( )
A.水中捞月 B.守株待兔 C.日出东方 D.拔苗助长
解:A、水中捞月,是不可能事件,故本选项不符合题意;
B、守株待兔,是随机事件,故本选项不符合题意;
C、日出东方,是必然事件,故本选项符合题意;
D、拔苗助长,是不可能事件,故本选项不符合题意;
故选:C.
5.在反比例函数图象的每一支曲线上,y都随x的增大而减小,则k的取值范围是( )
A.k>3 B.k>0 C.k<3 D.k<0
解:在图象的每一支曲线上,y都随x的增大而减小,根据反比例函数的性质,
得k﹣3>0,
k>3.
故选:A.
6.一元二次方程x2+2x+m=0有两个不相等的实数根,则( )
A.m>3 B.m=3 C.m<3 D.m≤3
解:∵一元二次方程x2+2x+m=0有两个不相等的实数根,
∴△=(2)2﹣4m>0,
解得:m<3.
故选:C.
7.圆的直径是13cm,如果圆心与直线上某一点的距离是6.5cm,那么该直线和圆的位置关系是( )
A.相离 B.相切 C.相交 D.相交或相切
解:∵圆的直径为13 cm,
∴圆的半径为6.5 cm,
∵圆心与直线上某一点的距离是6.5cm,
∴圆的半径≥圆心到直线的距离,
∴直线于圆相切或相交,
故选:D.
8.已知圆锥的底面半径长为5,侧面展开后得到一个半圆,则该圆锥的母线长为( )
A.2.5 B.5 C.10 D.15
解:设母线长为x,根据题意得
2πx÷2=2π×5,
解得x=10.
故选:C.
9.二次函数y=ax2+bx+c的图象如图所示,则一次函数y=bx+b2﹣4ac与反比例函数y=在同一坐标系内的图象大致为( )
A. B.
C. D.
解:由抛物线的图象可知,横坐标为1的点,即(1,a+b+c)在第四象限,因此a+b+c<0;
∴双曲线的图象在第二、四象限;
由于抛物线开口向上,所以a>0;
对称轴x=>0,所以b<0;
抛物线与x轴有两个交点,故b2﹣4ac>0;
∴直线y=bx+b2﹣4ac经过第一、二、四象限.
故选:D.
10.如图,半径为4的⊙O中,CD为直径,弦AB⊥CD且过半径OD的中点,点E为⊙O上一动点,CF⊥AE于点F.当点E从点B出发顺时针运动到点D时,点F所经过的路径长为( )
A. B. C. D.
解:连接AC,AO,
∵AB⊥CD,
∴G为AB的中点,即AG=BG=AB,
∵⊙O的半径为4,弦AB⊥CD且过半径OD的中点,
∴OG=2,
∴在Rt△AOG中,根据勾股定理得:AG==2,
又∵CG=CO+GO=4+2=6,
∴在Rt△AGC中,根据勾股定理得:AC==4,
∵CF⊥AE,
∴△ACF始终是直角三角形,点F的运动轨迹为以AC为直径的半圆,
当E位于点B时,CG⊥AE,此时F与G重合;当E位于D时,CA⊥AE,此时F与A重合,
∴当点E从点B出发顺时针运动到点D时,点F所经过的路径长,
在Rt△ACG中,tan∠ACG==,
∴∠ACG=30°,
∴所对圆心角的度数为60°,
∵直径AC=4,
∴的长为=π,
则当点E从点B出发顺时针运动到点D时,点F所经过的路径长为π.
故选:C.
二、填空题(本大题共6小题,每小题3分,共18分)
11.若有意义,则x的取值范围为 x≤且x≠﹣1 .
解:由题意得:1﹣2x≥0,且x+1≠0,
解得:x≤且x≠﹣1,
故答案为:x≤且x≠﹣1.
12.把抛物线y=2x2先向下平移1个单位,再向左平移2个单位,得到的抛物线的解析式是 y=2(x+2)2﹣1 .
解:由“上加下减”的原则可知,二次函数y=2x2的图象向下平移1个单位得到y=2x2﹣1,
由“左加右减”的原则可知,将二次函数y=2x2﹣1的图象向左平移2个单位可得到函数y=2(x+2)2﹣1,
故答案是:y=2(x+2)2﹣1.
13.一个不透明的口袋中有四个完全相同的小球,把它们分别标号为1、2、3、4.随机摸取一个小球然后放回,再随机摸出一个小球,两次取出的小球标号的和等于5的概率是 .
解:画树状图如下:
随机地摸出一个小球,然后放回,再随机地摸出一个小球,共有16种等可能的结果数,其中两次摸出的小球标号的和等于5的占4种,
所有两次摸出的小球标号的和等于5的概率为=,
故答案为:.
14.设计人体雕像时,使雕像的上部(腰以上)与下部(腰以下)的高度比,等于下部与全部(全身)的高度比,可以增加视觉美感.按此比例,如果雕像的高为2m,那么上部应设计为多高?设雕像的上部高xm,列方程,并化成一般形式是 x2﹣6x+4=0 .
解:设雕像的上部高x m,则题意得:
,
整理得:x2﹣6x+4=0,
故答案为:x2﹣6x+4=0
15.如图,正六边形ABCDEF中,P是边ED的中点,连接AP,则= .
解:连接AE,过点F作FH⊥AE,
∵六边形ABCDEF是正六边形,
∴AB=BC=CD=DE=EF=a,
∠AFE=∠DEF=120°,
∴∠FAE=∠FEA=30°,
∴∠AEP=90°,
∴FH=,
∴AH=,AE=,
∵P是ED的中点,
∴EP=,
∴AP=.
∴=
16.如图,∠AOB=30°,点M,N分别是射线OA,OB上的动点,OP平分∠AOB,且OP=6,当△PMN的周长取最小值时,MN的长为 12﹣18 .
解:设点P关于OA的对称点为C,关于OB的对称点为D,连接OC,OD,CD,CD分别交OA、OB于点M'、N',连接PM'、PN',如图所示:
∵点P关于OA的对称点为C,关于OB的对称点为D,
∴PM'=CM',OP=OC,∠COA=∠POA;PN'=DN',OP=OD,∠DOB=∠POB.
∴OC=OD=OP=6,
∵∠AOB=30°,
∴∠COD=∠COA+∠AOP+∠POB+∠BOD
=2∠AOP+2∠POB
=2∠AOB
=60°,
∴△COD是等边三角形,
∴CD=OC=OD=6,
∵OP平分∠AOB,
∴∠POC=∠POD,
∴OP⊥CD,
∴OQ=6sin60°=6×=3,
∴PQ=6﹣3,
设M'Q=x,则PM'=CM'=3﹣x,
∴(3﹣x)2﹣x2=,
解得x=6﹣9.
∴M'N'=2x=12﹣18.
故答案为:12﹣18.
三、解答题(本大题共9小题,共72分)
17.解方程:(x+1)2+2x(x+1)=0.
解:∵(x+1)2+2x(x+1)=0,
∴(x+1)(3x+1)=0,
则x+1=0或3x+1=0,
解得x1=﹣1,x2=﹣.
18.如图,在平面直角坐标系xOy中,A(﹣2,0),B(0,3),C(﹣4,1).以原点O为旋转中心,将△ABC顺时针旋转90°得到△A'B'C',其中点A,B,C旋转后的对应点分别为点A',B',C',画出△A'B'C',并写出点A',B',C'的坐标.
解:如图,△A'B'C'为所作,点A',B',C'的坐标分别为(0,2),(3,0),(1,4).
19.有红、白、蓝三种颜色的小球各一个,它们除颜色外没有其它任何区别.现将3个小球放入编号为①、②、③的三个盒子里,规定每个盒子里放一个,且只能放一个小球.请用树状图或其它适当的形式列举出3个小球放入盒子的所有可能情况,并求红球恰好被放入②号盒子的概率.
解:画树状图如下,
由树状图知,共有6种等可能结果,其中红球恰好被放入②号盒子的有2种结果,
∴红球恰好被放入②号盒子的概率为=.
20.如图,已知AD?AC=AB?AE,∠DAE=∠BAC.求证:∠DBA=∠ECA.
【解答】证明:∵AD?AC=AB?AE,
∴=,
∴∠DAE=∠BAC,
∴∠DAE﹣∠BAE=∠BAC﹣∠BAE,
即∠DAB=∠EAC,
∴△ADB∽△AEC,
∴∠DBA=∠ECA.
21.如图,在⊙O中,∠ACB=∠BDC=60°,AC=2cm.
(1)求∠BAC的度数;(2)求⊙O的周长.
解:(1)∠BAC=∠BDC=60°(同弧所对的圆周角相等);
(2)∠ABC=180°﹣∠BAC﹣∠ACB=60°,
∴△ABC是等边三角形,
作OE⊥AC于点E,连接OA,则OA平分∠BAC,
∴∠OAE=30°,
∴OA==2cm,
所以⊙O的周长=2π×2=4πcm.
22.投资1万元围成一个矩形菜园(如图),其中一边靠墙,另外三边选用不同材料建造,墙长24m,平行于墙的边的费用为200元/m,垂直于墙的边的费用为150元/m,设平行于墙的边长为xm.
(1)设垂直于墙的一边长为ym,直接写出y与x之间的函数关系式.
(2)若菜园的面积为384m2,求x的值.
(3)求菜园的最大面积.
解:(1)根据题意知,y==﹣x+(0<x≤24);
(2)根据题意,得:(﹣x+)x=384,
解得:x=18或x=32,
∵墙的长度为24m,
∴x=18;
(3)设菜园的面积是S,
则S=(=﹣x+)x
=﹣x2+x
=﹣(x﹣25)2+,
∵﹣<0,
∴当x<25时,S随x的增大而增大,
∵x≤24,
∴当x=24时,S取得最大值,最大值为416,
答:菜园的最大面积为416m2.
23.如图,在四边形OABC中,BC∥AO,∠AOC=90°,点A(5,0),B(2,6),点D为AB上一点,且=,双曲线y1=(k1>0)在第一象限的图象经过点D,交BC于点E.
(1)求双曲线的解析式.
(2)一次函数的=k2x+b经过D、E两点,结合图象,写出不等式<k2x+b的解集.
解:(1)作BM⊥x轴于M,作DN⊥x轴于N,如图,
点A,B的坐标分别为(5,0),(2,6),
∴BC=OM=2,BM=OC=6,AM=3,
∵DN∥BM,
∴△AND∽△ABM,
∴,即,
∴DN=2,AN=1,
∴ON=OA﹣AN=4,
∴D点坐标为(4,2),
把D(4,2)代入y=得k1=2×4=8,
∵反比例函数解析式为y=;
(2)将y=6入y=中,得:x=,
故E(,6),
由图象可知,不等式<k2x+b的解集为<x<6.
24.如图,二次函数y=x2﹣2x+1图象与一次函数y=kx+b(k≠0)的图象交于A,B两点,点A的坐标为(0,1),点B在第一象限内,点C是二次函数图象的顶点,点M是一次函数y=kx+b(k≠0)的图象与x轴的交点,过点B作x轴的垂线,垂足为N,且S△AMO:S四边形AONB=1:48.
(1)求直线AB和直线BC的解析式.
(2)点P是线段AB上一点,点D是线段BC上一点,PD∥x轴,射线PD与抛物线交于点G,过点P作PE⊥x轴于点E,PF⊥BC于点F,当PF与PE的乘积最大时,在线段AB上找一点H(不与点A,点B重合),使GH+BH的值最小,求点H的坐标和GH+BH的最小值.
解:(1)∵BN⊥x轴,
∴BN∥OA,
∴△MAO∽△MBN,
∵S△AMO:S四边形AONB=1:48,即S△AMO:S△MNB=1:49,
∴BN=7OA=7,
即yB=7,令y=x2﹣2x+1=7,解得x=6(不合题意的值已舍去),
故点B的坐标为(6,7),
设直线AB的表达式为y=kx+b,则,解得,
故直线AB的表达式为y=x+1,
由点B、C的坐标,同理可得,直线BC的表达式为y=2x﹣5;
(2)设点P的坐标为(m,m+1),
当y=m+1=2x﹣5时,解得x=3+m,故点D的坐标为(3+m,m+1),
则PD=3+m﹣m=3﹣m,PE=m+1,
∵∠PDF为定值,故PD:PF为定值,
故PD×PE最大时PF×PE也最大,
则PD×PE=(3﹣m)(m+1)=﹣m2+m+3,
∴当m=时,PD×PE最大,
此时,点P的坐标为(,),
令y=x2﹣2x+1=,解得x=5(不合题意的值已舍去),
故点G的坐标为(5,);
过点H作HN∥y轴交过点B与x轴的平行线于点N,连接HG,
由直线AB的表达式知,直线AB与x轴的夹角为45°,则∠NBH=45°,
故NH=BH,
故GH+BH=GH+NH,
故当G、N、H三点共线时,GH+BH取得最小值.
当x=5时,y=x+1=6,故点H的坐标为(5,6);
GH+BH的最小值=yB﹣yG=7﹣=.
25.如图,⊙O的直径AB为10cm,弦AC为6cm,∠ACB的平分线交⊙O于点D.
(1)求AD的长;
(2)试探究CA、CB、CD之间的等量关系,并证明你的结论;
(3)连接OD,P为半圆ADB上任意一点,过P点作PE⊥OD于点E,设△OPE的内心为M,当点P在半圆上从点B运动到点A时,求内心M所经过的路径长.
解:(1)∵AB是⊙O的直径,
∴∠ACB=∠ADB=90°,
∵∠ACB的平分线交⊙O于D,
∴∠ACD=∠BCD=45°,
∴=,
∴AD=BD,
∴AD2+BD2=AB2,
∴AD=BD=AB=×10=5;
(2)CA+CB=CD.
证明如下:延长CA到F,使AF=CB,连接DF,
∵∠CBD+∠CAD=180°,∠FAD+∠CAD=180°,
∴∠CBD=∠FAD,
在△ADF和△BDC中,
,
∴△ADF≌△BDC(SAS),
∴CD=FD,∠CDB=∠FDA,
∴∠CDF=∠ADB=90°,△CDF为等腰直角三角形,
∴CA+CB=CF=CD.
(3)连接OM,PM,
∵PE⊥OD,
∴∠PEO=90°,
∵点M为△OPE的内心,
∴∠OMP=135°,
在△OMD和△OMP中,
,
∴△OMD≌△OMP(SAS),
∴∠OMD=∠OMP=135°,
∴点M在以OD为弦,并且所对的圆周角为135°的两段劣弧上(分OD左右两种情况):
设弧OMD所在圆的圆心为O',
∵∠OMD=135°,
∴∠OO'D=90°,
∴O'O=OD=,
∴的长为=π,
∴点M的路径长为π.
同课章节目录
