9.2《实际问题与一元一次不等式》精品课件(人教版七年级)
文档属性
| 名称 | 9.2《实际问题与一元一次不等式》精品课件(人教版七年级) |

|
|
| 格式 | zip | ||
| 文件大小 | 380.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2012-02-27 00:00:00 | ||
图片预览






文档简介
(共15张PPT)
我店累计购买100元商品后,再购买的商品按原价的90%收费
甲
我店累计购买50元商品后,再购买的商品按原价的95%收费
乙
甲商店购物款达多少元后可以优惠?
乙商店购物款达多少元后可以优惠?
我探究、我发现
我店累计购买100元商品后,再购买的商品按原价的90%收费。
我店累计购买50元商品后,再购买的商品按原价的95%收费。
甲
乙
我探究、我发现
如果你要分别购买40元、80 元、140元、160元商品,应该去哪家商店更优惠?
甲店:
100+40×90%=136(元)
乙店:
50+90 ×95%=135.5(元)
甲店
乙店
>
甲店:
100+60×90%=154(元)
50+110×95%=154.5(元)
乙店:
甲店<乙店
当购买140元商品时:
当购买160元商品时:
分析:
乙店消费>甲店消费
解:
设累计购物x元(x>100),如果在甲店购物花费小,则
50+0.95(x-50)
100+0.9(x-100)
>
去括号得:
50+0.95x-47.5>100+0.9x-90
移项且合并得:
0.05x>7.5
系数化为1得:
X >150
∴累计购物超过150元时在甲店购物花费小。
如果累计购物超过100元,那么在
甲店购物花费小吗?
思考:
1
2
3
4
5
6
7
8
-1
-2
-3
-4
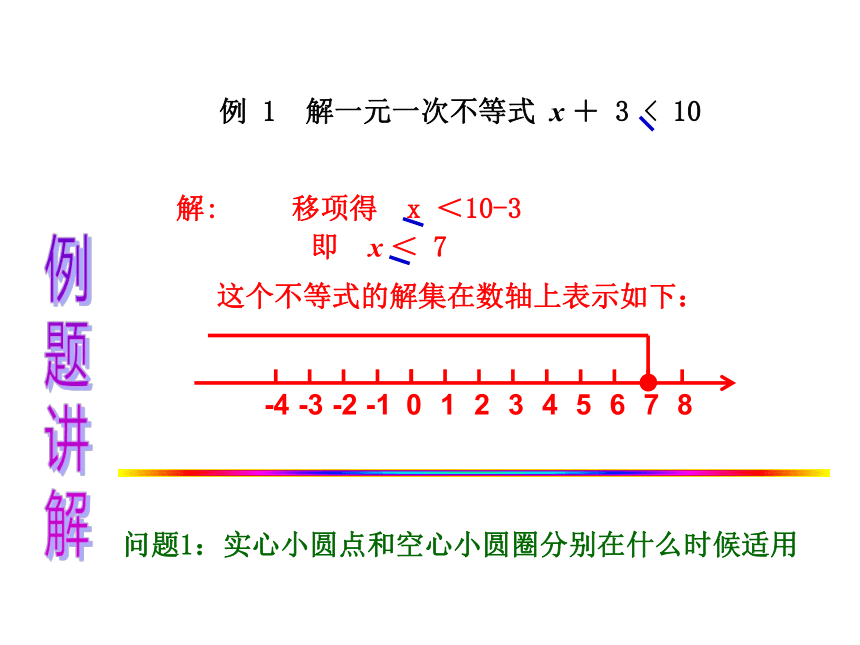
解: 移项得 x <10-3
例 1 解一元一次不等式 x + 3 < 10
即 x < 7
这个不等式的解集在数轴上表示如下:
0
问题1:实心小圆点和空心小圆圈分别在什么时候适用
解一元一次不等式 8x-2≤7x+3,并把它的解在数轴上表示出来。
例2
解:移项,得
0
1
2
3
4
5
6
7
-1
x
8x- 7x ≤3+2
∴ x ≤5
这个不等式的解集在数轴上表示如下:
思考:求满足不等式 8x-2≤7x+3 的正整数解
8x-2≤7x+3
8x-7x≤3+2
x + 3 < 10
x<10 - 3
+ 3
-3
7x
-7x
-2
+2
再说一遍:移项要变号,不影响不等号的方向
例3 解不等式
3(1-x)>2(1-2x)
解: 去括号,得 3-3 x >2-4x
移项,得 -3 x +4x >-3+2
合并同类项,得 x >-1
∴原不等式的解集是x >-1
解下列不等式,并在数轴上表示解集:
移项得:
5x-4x>-1-15
合并得
X>-16
解集在数轴上的表示如图
0
-16
去括号得:
3x+15>4x-1
解:(1)
解:
移项得:
2x-3x<-10-15
合并得:
-X<-25
解集在数轴上的表示如图
(2) 2(x+5)<3(x-5)
去括号得:
2x+10<3x-15
x>25
25
0
5
系数化为1得:
1) 当x 时式子-2x-8的值是正数。
2) 若式子2x-1不大于3x-4则x的取
值范围是 。
3) 不等式2x-1≤3x的负整数解是 。
<-4
x≥3
-1
做一做
2.x取哪些非负整数时, 的值不小于 与1的差。
3. 矩形一边长10cm,为使它的周长不小于边长为6cm的正方形的周长,这个矩形的另一边长怎样?
5.甲有存款800元,乙有存款2000元。由本月开始,甲每月存500元,乙每月存200元,那么到了第几个月,甲的存款能超过乙的存款?
二、应用一元一次不等式解实际问题的一般步骤:
实际问题
(包含不等关系)
数学问题
(一元一次不等式)
数学问题的解
(不等式的解集)
实际问题的解答
设未知数,列不等式
检验
解不等式
1、去分母 (不等式的性质2)
2、去括号 (乘法分配律)
3、移项 (不等式的性质1)
4、合并同类项 (整式加减性质)
5、化系数为1 (不等式的性质2,3)
一、解不等式的基本步骤
我店累计购买100元商品后,再购买的商品按原价的90%收费
甲
我店累计购买50元商品后,再购买的商品按原价的95%收费
乙
甲商店购物款达多少元后可以优惠?
乙商店购物款达多少元后可以优惠?
我探究、我发现
我店累计购买100元商品后,再购买的商品按原价的90%收费。
我店累计购买50元商品后,再购买的商品按原价的95%收费。
甲
乙
我探究、我发现
如果你要分别购买40元、80 元、140元、160元商品,应该去哪家商店更优惠?
甲店:
100+40×90%=136(元)
乙店:
50+90 ×95%=135.5(元)
甲店
乙店
>
甲店:
100+60×90%=154(元)
50+110×95%=154.5(元)
乙店:
甲店<乙店
当购买140元商品时:
当购买160元商品时:
分析:
乙店消费>甲店消费
解:
设累计购物x元(x>100),如果在甲店购物花费小,则
50+0.95(x-50)
100+0.9(x-100)
>
去括号得:
50+0.95x-47.5>100+0.9x-90
移项且合并得:
0.05x>7.5
系数化为1得:
X >150
∴累计购物超过150元时在甲店购物花费小。
如果累计购物超过100元,那么在
甲店购物花费小吗?
思考:
1
2
3
4
5
6
7
8
-1
-2
-3
-4
解: 移项得 x <10-3
例 1 解一元一次不等式 x + 3 < 10
即 x < 7
这个不等式的解集在数轴上表示如下:
0
问题1:实心小圆点和空心小圆圈分别在什么时候适用
解一元一次不等式 8x-2≤7x+3,并把它的解在数轴上表示出来。
例2
解:移项,得
0
1
2
3
4
5
6
7
-1
x
8x- 7x ≤3+2
∴ x ≤5
这个不等式的解集在数轴上表示如下:
思考:求满足不等式 8x-2≤7x+3 的正整数解
8x-2≤7x+3
8x-7x≤3+2
x + 3 < 10
x<10 - 3
+ 3
-3
7x
-7x
-2
+2
再说一遍:移项要变号,不影响不等号的方向
例3 解不等式
3(1-x)>2(1-2x)
解: 去括号,得 3-3 x >2-4x
移项,得 -3 x +4x >-3+2
合并同类项,得 x >-1
∴原不等式的解集是x >-1
解下列不等式,并在数轴上表示解集:
移项得:
5x-4x>-1-15
合并得
X>-16
解集在数轴上的表示如图
0
-16
去括号得:
3x+15>4x-1
解:(1)
解:
移项得:
2x-3x<-10-15
合并得:
-X<-25
解集在数轴上的表示如图
(2) 2(x+5)<3(x-5)
去括号得:
2x+10<3x-15
x>25
25
0
5
系数化为1得:
1) 当x 时式子-2x-8的值是正数。
2) 若式子2x-1不大于3x-4则x的取
值范围是 。
3) 不等式2x-1≤3x的负整数解是 。
<-4
x≥3
-1
做一做
2.x取哪些非负整数时, 的值不小于 与1的差。
3. 矩形一边长10cm,为使它的周长不小于边长为6cm的正方形的周长,这个矩形的另一边长怎样?
5.甲有存款800元,乙有存款2000元。由本月开始,甲每月存500元,乙每月存200元,那么到了第几个月,甲的存款能超过乙的存款?
二、应用一元一次不等式解实际问题的一般步骤:
实际问题
(包含不等关系)
数学问题
(一元一次不等式)
数学问题的解
(不等式的解集)
实际问题的解答
设未知数,列不等式
检验
解不等式
1、去分母 (不等式的性质2)
2、去括号 (乘法分配律)
3、移项 (不等式的性质1)
4、合并同类项 (整式加减性质)
5、化系数为1 (不等式的性质2,3)
一、解不等式的基本步骤
