8.3《实际问题与二元一次方程组2》精品课件(人教版七年级)
文档属性
| 名称 | 8.3《实际问题与二元一次方程组2》精品课件(人教版七年级) |  | |
| 格式 | zip | ||
| 文件大小 | 227.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2012-02-27 22:18:24 | ||
图片预览

文档简介
(共14张PPT)
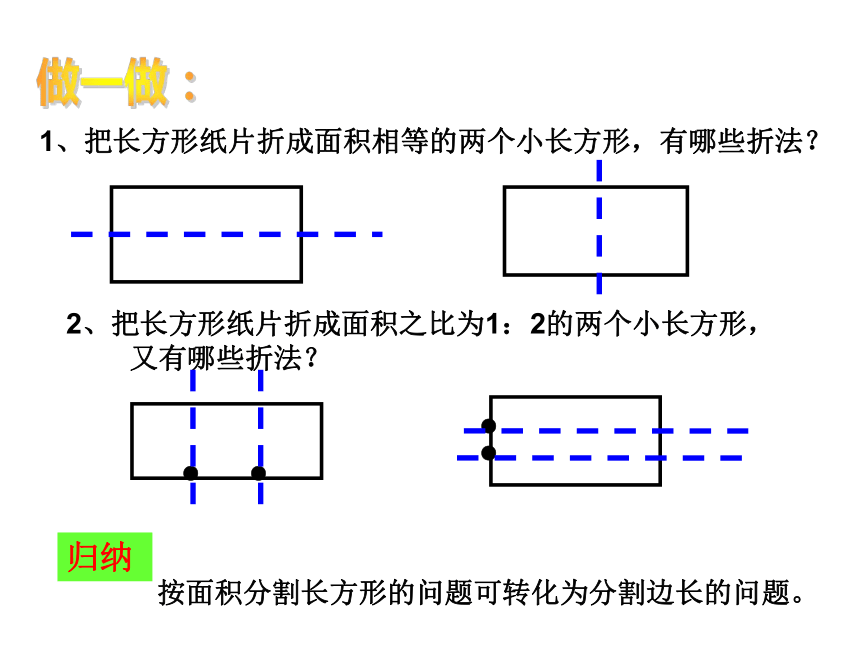
1、把长方形纸片折成面积相等的两个小长方形,有哪些折法?
2、把长方形纸片折成面积之比为1:2的两个小长方形,
又有哪些折法?
●
●
●
●
按面积分割长方形的问题可转化为分割边长的问题。
归纳
y
x
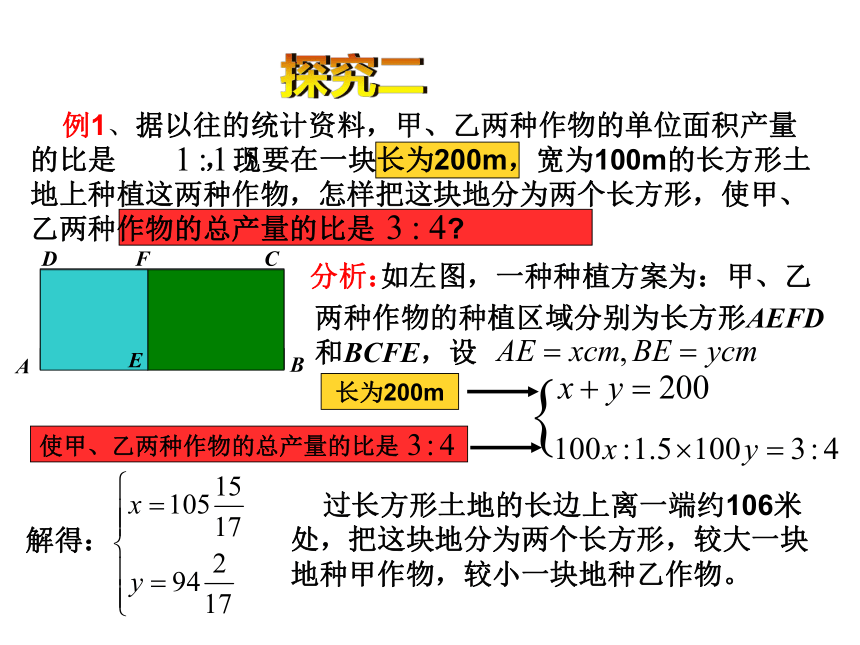
分析:
如左图,一种种植方案为:甲、乙
两种作物的种植区域分别为长方形AEFD和BCFE,设
使甲、乙两种作物的总产量的比是
长为200m
解得:
过长方形土地的长边上离一端约106米处,把这块地分为两个长方形,较大一块地种甲作物,较小一块地种乙作物。
B
A
E
C
F
D
例1、据以往的统计资料,甲、乙两种作物的单位面积产量的比是 ,现要在一块长为200m,宽为100m的长方形土地上种植这两种作物,怎样把这块地分为两个长方形,使甲、乙两种作物的总产量的比是
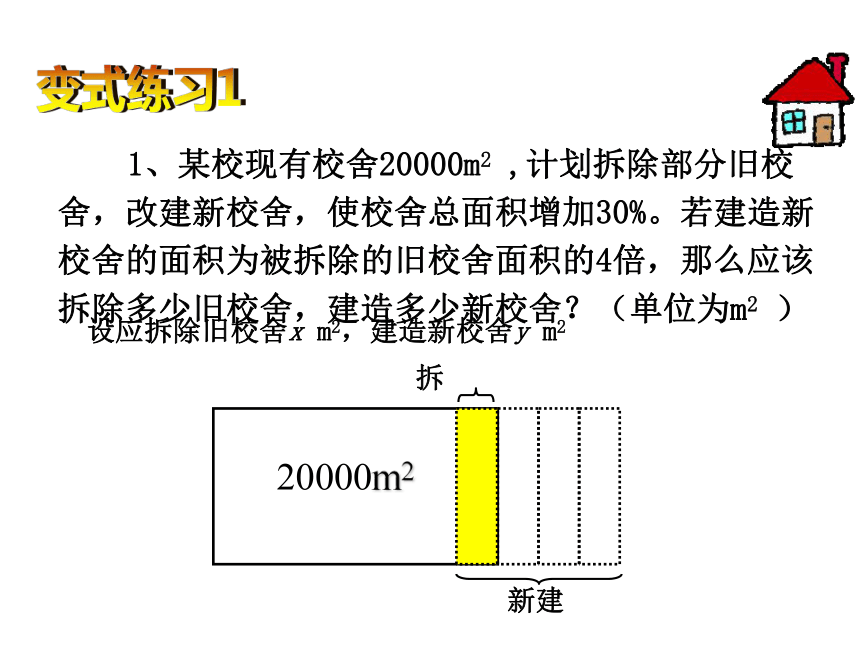
1、某校现有校舍20000m2 ,计划拆除部分旧校舍,改建新校舍,使校舍总面积增加30%。若建造新校舍的面积为被拆除的旧校舍面积的4倍,那么应该拆除多少旧校舍,建造多少新校舍?(单位为m2 )
设应拆除旧校舍x m2,建造新校舍y m2
拆
20000m2
新建
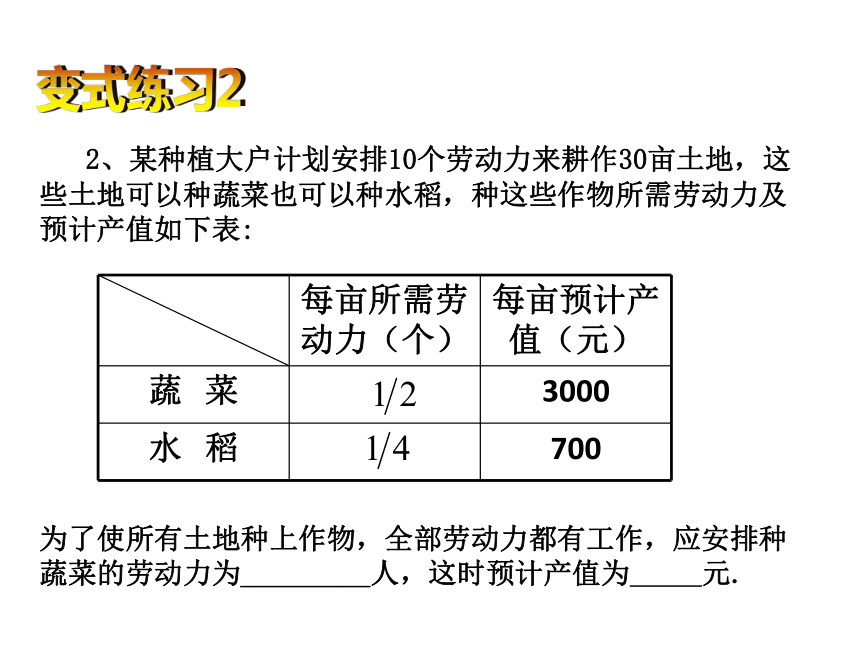
2、某种植大户计划安排10个劳动力来耕作30亩土地,这些土地可以种蔬菜也可以种水稻,种这些作物所需劳动力及预计产值如下表:
为了使所有土地种上作物,全部劳动力都有工作,应安排种蔬菜的劳动力为_________人,这时预计产值为 元.
每亩所需劳动力(个) 每亩预计产值(元)
蔬 菜 3000
水 稻 700
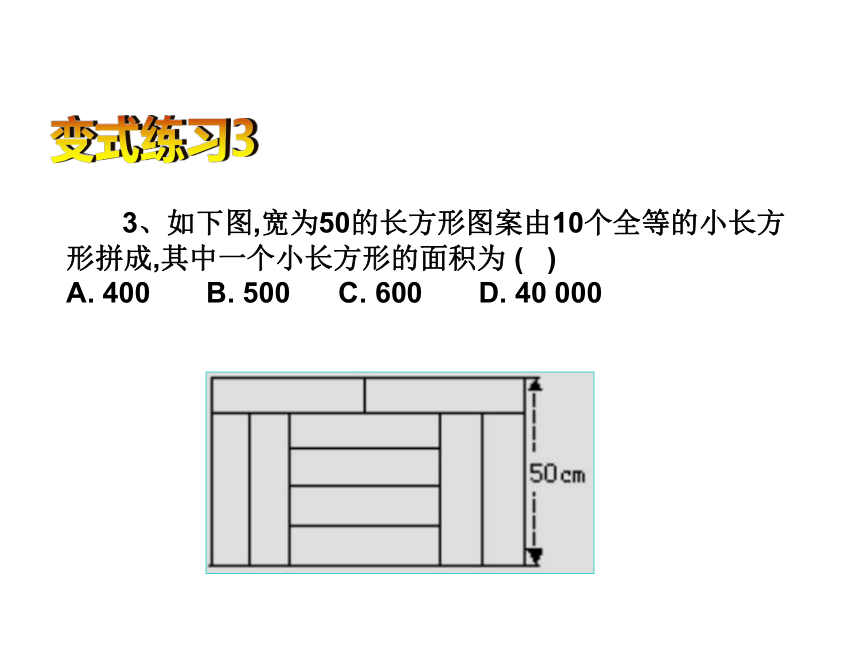
3、如下图,宽为50的长方形图案由10个全等的小长方形拼成,其中一个小长方形的面积为 ( )
A. 400 B. 500 C. 600 D. 40 000
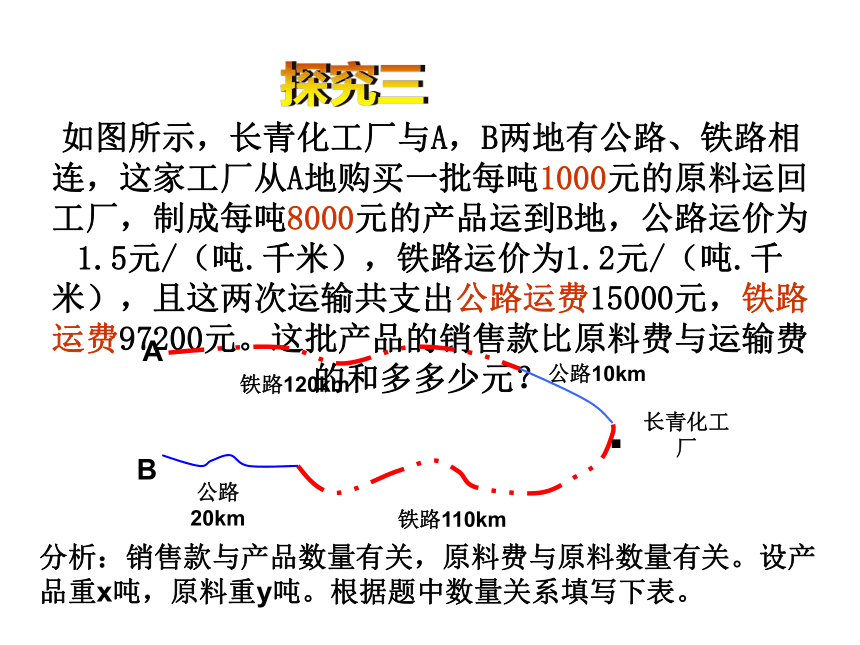
如图所示,长青化工厂与A,B两地有公路、铁路相连,这家工厂从A地购买一批每吨1000元的原料运回工厂,制成每吨8000元的产品运到B地,公路运价为1.5元/(吨.千米),铁路运价为1.2元/(吨.千米),且这两次运输共支出公路运费15000元,铁路运费97200元。这批产品的销售款比原料费与运输费的和多多少元?
A
B
铁路120km
公路10km
.
长青化工厂
铁路110km
公路20km
分析:销售款与产品数量有关,原料费与原料数量有关。设产品重x吨,原料重y吨。根据题中数量关系填写下表。
产品x吨 原料y吨 合计
公路运费(元)
铁路运费(元)
价 值(元)
1.5×20x
1.5×10y
1.5×(20x+10y)
1.2×110x
1.2×120y
1.2×(110x+120y)
8000x
1000y
由上表,列方程组
,
。
解这个方程组得:
X= ,
y = 。
因此,这批产品的销售款比原料费与运输费的和多 元。
1.5×(20x+10y)=15000
1.2×(110x+120y)=97200
300
400
1887800
1、 张强与李毅二人分别从相距 20 千米的两地出发,相向而行。若张强比李毅早出发 30 分钟,那么在李毅出发后 2 小时,他们相遇;如果他们同时出发,那么 1 小时后两人还相距 11 千米。求张强、李毅每小时各走多少千米?
2y千米
张强2.5小时走的路程
李毅2小时走的路程
11千米
0.5x千米
2x千米
(1)
A
B
x千米
y千米
(2)
A
B
答:张强、李毅每小时各走4, 5千米
分析:
解设:张强、李毅每小时各走x, y千米
2、我国的长江由西至东奔腾不息,其中九江东至南京约有450千米的路程,某船从九江出发九个小时就能到达南京;返回时则用多了一个小时。求此船在静水中的速度以及长江水的平均流速 。
解:设轮船在静水中的速度为x千米/时,长江水的平均流速为y千米/时。
速度×时间=路程
顺流的情况:(轮船静水速度+水速)×时间1=路程
逆流的情况:(轮船静水速度-水速)×时间2=路程
( x + y )× 9 =450
( x - y )× 10 =450
答:轮船在静水中的速度为47.5千米/时,长江水的平均流速为2.5千米/时。
小明骑摩托车在公路上保持相同的速度高速行驶,12:00时看到里程碑上的数是一个两位数,它的数字之和是7;13:00时看里程碑上的两位数与12:00时看到的个位数和十位数颠倒 了;14:00时看到里程碑上的数比12:00时看到的两位数中间多了个零,小明在12:00时看到里程碑上的数字是少?
解:设小明在12:00时看到的数的十位数字是x,个位的
数字是y,那么
答:小明在12:00时看到的数字是16.
x=1
y=6
解得
如果去掉它的数字之和是7这个条件,你能计算出这个两位数是多少吗
x+y=7
(10y+x)-(10x+y)=(100x+y)-(10y+x)
实际问题
设未知数、找等量关系、列方程(组)
数学问题
[方程(组)]
解方程(组)
数学问题的解
双检验
实际问题
的答案
1、把长方形纸片折成面积相等的两个小长方形,有哪些折法?
2、把长方形纸片折成面积之比为1:2的两个小长方形,
又有哪些折法?
●
●
●
●
按面积分割长方形的问题可转化为分割边长的问题。
归纳
y
x
分析:
如左图,一种种植方案为:甲、乙
两种作物的种植区域分别为长方形AEFD和BCFE,设
使甲、乙两种作物的总产量的比是
长为200m
解得:
过长方形土地的长边上离一端约106米处,把这块地分为两个长方形,较大一块地种甲作物,较小一块地种乙作物。
B
A
E
C
F
D
例1、据以往的统计资料,甲、乙两种作物的单位面积产量的比是 ,现要在一块长为200m,宽为100m的长方形土地上种植这两种作物,怎样把这块地分为两个长方形,使甲、乙两种作物的总产量的比是
1、某校现有校舍20000m2 ,计划拆除部分旧校舍,改建新校舍,使校舍总面积增加30%。若建造新校舍的面积为被拆除的旧校舍面积的4倍,那么应该拆除多少旧校舍,建造多少新校舍?(单位为m2 )
设应拆除旧校舍x m2,建造新校舍y m2
拆
20000m2
新建
2、某种植大户计划安排10个劳动力来耕作30亩土地,这些土地可以种蔬菜也可以种水稻,种这些作物所需劳动力及预计产值如下表:
为了使所有土地种上作物,全部劳动力都有工作,应安排种蔬菜的劳动力为_________人,这时预计产值为 元.
每亩所需劳动力(个) 每亩预计产值(元)
蔬 菜 3000
水 稻 700
3、如下图,宽为50的长方形图案由10个全等的小长方形拼成,其中一个小长方形的面积为 ( )
A. 400 B. 500 C. 600 D. 40 000
如图所示,长青化工厂与A,B两地有公路、铁路相连,这家工厂从A地购买一批每吨1000元的原料运回工厂,制成每吨8000元的产品运到B地,公路运价为1.5元/(吨.千米),铁路运价为1.2元/(吨.千米),且这两次运输共支出公路运费15000元,铁路运费97200元。这批产品的销售款比原料费与运输费的和多多少元?
A
B
铁路120km
公路10km
.
长青化工厂
铁路110km
公路20km
分析:销售款与产品数量有关,原料费与原料数量有关。设产品重x吨,原料重y吨。根据题中数量关系填写下表。
产品x吨 原料y吨 合计
公路运费(元)
铁路运费(元)
价 值(元)
1.5×20x
1.5×10y
1.5×(20x+10y)
1.2×110x
1.2×120y
1.2×(110x+120y)
8000x
1000y
由上表,列方程组
,
。
解这个方程组得:
X= ,
y = 。
因此,这批产品的销售款比原料费与运输费的和多 元。
1.5×(20x+10y)=15000
1.2×(110x+120y)=97200
300
400
1887800
1、 张强与李毅二人分别从相距 20 千米的两地出发,相向而行。若张强比李毅早出发 30 分钟,那么在李毅出发后 2 小时,他们相遇;如果他们同时出发,那么 1 小时后两人还相距 11 千米。求张强、李毅每小时各走多少千米?
2y千米
张强2.5小时走的路程
李毅2小时走的路程
11千米
0.5x千米
2x千米
(1)
A
B
x千米
y千米
(2)
A
B
答:张强、李毅每小时各走4, 5千米
分析:
解设:张强、李毅每小时各走x, y千米
2、我国的长江由西至东奔腾不息,其中九江东至南京约有450千米的路程,某船从九江出发九个小时就能到达南京;返回时则用多了一个小时。求此船在静水中的速度以及长江水的平均流速 。
解:设轮船在静水中的速度为x千米/时,长江水的平均流速为y千米/时。
速度×时间=路程
顺流的情况:(轮船静水速度+水速)×时间1=路程
逆流的情况:(轮船静水速度-水速)×时间2=路程
( x + y )× 9 =450
( x - y )× 10 =450
答:轮船在静水中的速度为47.5千米/时,长江水的平均流速为2.5千米/时。
小明骑摩托车在公路上保持相同的速度高速行驶,12:00时看到里程碑上的数是一个两位数,它的数字之和是7;13:00时看里程碑上的两位数与12:00时看到的个位数和十位数颠倒 了;14:00时看到里程碑上的数比12:00时看到的两位数中间多了个零,小明在12:00时看到里程碑上的数字是少?
解:设小明在12:00时看到的数的十位数字是x,个位的
数字是y,那么
答:小明在12:00时看到的数字是16.
x=1
y=6
解得
如果去掉它的数字之和是7这个条件,你能计算出这个两位数是多少吗
x+y=7
(10y+x)-(10x+y)=(100x+y)-(10y+x)
实际问题
设未知数、找等量关系、列方程(组)
数学问题
[方程(组)]
解方程(组)
数学问题的解
双检验
实际问题
的答案
