9.1.2《不等式的性质》精品课件(人教版七年级)
文档属性
| 名称 | 9.1.2《不等式的性质》精品课件(人教版七年级) |

|
|
| 格式 | zip | ||
| 文件大小 | 500.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2012-02-27 00:00:00 | ||
图片预览





文档简介
(共16张PPT)
用“>”或“<”表示大小关系的式子叫做不等式.
用“≠”表示不等关系的式子也叫不等式.
用“≥”或“≤”表示大小关系的式子叫做不等式.
“≥”读作“大于或等于”或“不小于”
“≤”读作
“小于或等于”或“不大于”
等式基本性质1:
等式的两边都加上(或减去)同一个整式,等式仍旧成立
等式基本性质2:
等式的两边都乘(或除以)同一个数(除数不为0),等式仍旧成立
如果a=b,那么a±c=b±c
如果a=b,那么ac=bc或 (c≠0),
不等式是否具有类似的性质呢?
如果 7 > 3
那么 7+5 ____ 3+ 5 , 7 -5____3-5
你能总结一下规律吗?
>
>
如果-1< 3,
那么-1+2____3+2, -1- 4____3 - 4
<
<
+ c
-c
(或________)
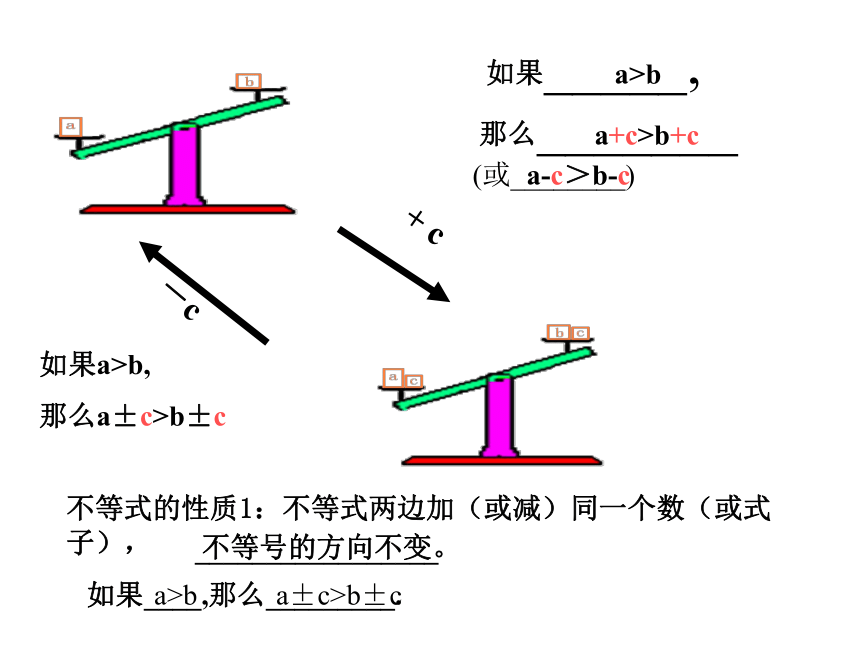
如果_____,
那么_______
如果a>b,
那么a±c>b±c
a>b
a+c>b+c
a-c>b-c
不等式的性质1:不等式两边加(或减)同一个数(或式子),
如果____,那么_________.
a>b
a±c>b±c
_________________
不等号的方向不变。
7÷5 ____ 3÷ 5 ,
7 ÷ (-5)____3÷ (-5)
不等式还有什么类似的性质呢?
如果 7 > 3
那么 7×5 ____ 3× 5 ,
7 ×(-5)____3×(-5),
你能再总结一下规律吗?
>
>
如果-1< 3,
那么-1×2____3×2,
-1×(- 4)____3×( - 4),
-1÷2____3÷2,
-1÷ (- 4)____3÷ ( - 4)
>
>
<
<
<
<
×3
÷3
(或 )
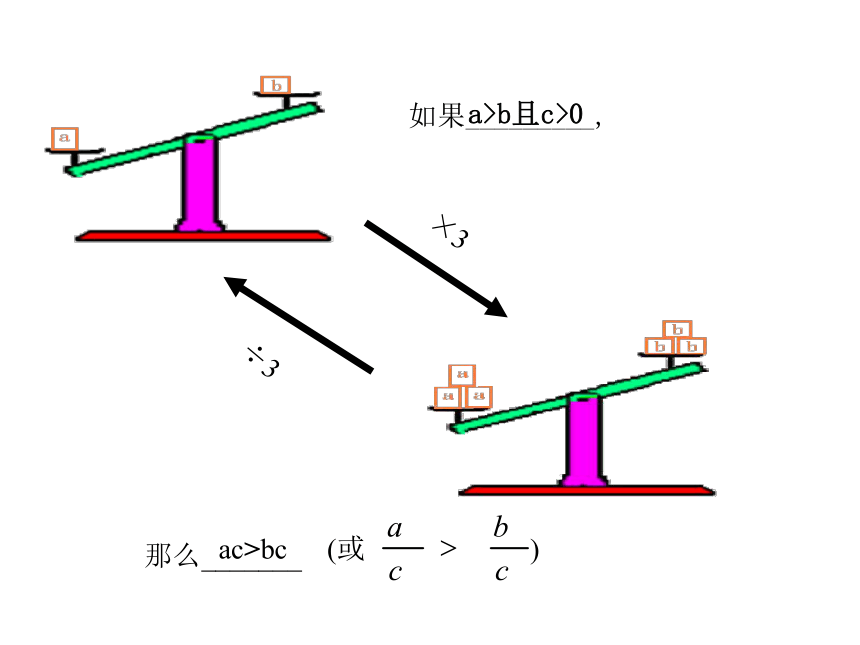
如果_________,
那么_______
a>b且c>0
ac>bc
不等式的性质2:不等式两边都乘(或除以)同一个____,不等号的方向____ 。
不等式的性质3:不等式两边都乘(或除以)同一个____,不等号的方向____。
如果 ________ ,那么 ______________
不变
正数
a>b,c>0
ac>bc (或 )
负数
改变
如果________,那么______________
a>b,c<0
ac例1、设a>b,用“<” 或“>”填空,并说出是根据哪条不等式性质。 典例精析
(1) 3a 3b;
(2) a-8 b-8;
(3) -2a -2b;
(4) 2a-5 2b-5;
(5) -3.5a-1 -3.5b-1.
>
>
<
<
>
不等式的性质2
不等式的性质1
不等式的性质3
不等式的性质1及2
不等式的性质1及3
练习: 已知a<0,用“<”或“>”号填空:
(1)a+2 ____2; (2)a-1 _____-1; (3)3a______ 0;
(4)-a/4______0; (5)a2_____0;
答:
(1)a+2<2,根据不等式的性质1.
(2)a-1<-1,根据不等式的性质1.
(3)3a<0,根据不等式的性质2.
(5)因为a<0,两边同乘a<0,
由不等式的性质3,得a2>0.
(4) -a/4>0,根据不等式的性质3.
将下列不等式化成x > a或 x < a 的形式,并说出根据.
(1) x- 7>26
(2) 3x < 2x +1
解:根据不等式的性质1 , 不等式两边都加上7,不等号方向不变,得, x >33
解:根据不等式的性质1,不等式两边都减去2x,不等号方向不变,得,x < 1
题目改为:利用不等式的性质解下列不等式, 并把解集在数轴上表示出来.
解:为了使不等式x- 7>26中不等号的一边变为x,根据不等式的性质1 , 不等式两边都加上7,不等号方向不变,得,
x- 7+7>26+7
x >33
这个不等式的解集在数轴上表示如下:
︱
0
○
33
锋 芒 初 试
利用不等式的性质解下列不等式,并在数轴上表示解集:
(1)3x<2x+1;
(2)x+5>-1;
(3)4x<3x-5.
我是最棒的
利用不等式的性质解下列不等式,并在数轴上表示解集:
(1) x>50;
(2) – 4x>3.
2
3
①在利用不等式的基本性质进行变形时,当不等式的两边都乘 (或除以)同一个字母,字母代表什么数是问题的关键,这决定了是用不等式的性质2还是性质3,也就是不等号是否要改变方向的问题;
②运用不等式的性质3时,要变两个号,一个是性质符号,另一个是不等号.
③ 补充两点:
(1)如果a>b,那么b<a 。
(2)如果a>b, b >c,那么 a > c。
用“>”或“<”表示大小关系的式子叫做不等式.
用“≠”表示不等关系的式子也叫不等式.
用“≥”或“≤”表示大小关系的式子叫做不等式.
“≥”读作“大于或等于”或“不小于”
“≤”读作
“小于或等于”或“不大于”
等式基本性质1:
等式的两边都加上(或减去)同一个整式,等式仍旧成立
等式基本性质2:
等式的两边都乘(或除以)同一个数(除数不为0),等式仍旧成立
如果a=b,那么a±c=b±c
如果a=b,那么ac=bc或 (c≠0),
不等式是否具有类似的性质呢?
如果 7 > 3
那么 7+5 ____ 3+ 5 , 7 -5____3-5
你能总结一下规律吗?
>
>
如果-1< 3,
那么-1+2____3+2, -1- 4____3 - 4
<
<
+ c
-c
(或________)
如果_____,
那么_______
如果a>b,
那么a±c>b±c
a>b
a+c>b+c
a-c>b-c
不等式的性质1:不等式两边加(或减)同一个数(或式子),
如果____,那么_________.
a>b
a±c>b±c
_________________
不等号的方向不变。
7÷5 ____ 3÷ 5 ,
7 ÷ (-5)____3÷ (-5)
不等式还有什么类似的性质呢?
如果 7 > 3
那么 7×5 ____ 3× 5 ,
7 ×(-5)____3×(-5),
你能再总结一下规律吗?
>
>
如果-1< 3,
那么-1×2____3×2,
-1×(- 4)____3×( - 4),
-1÷2____3÷2,
-1÷ (- 4)____3÷ ( - 4)
>
>
<
<
<
<
×3
÷3
(或 )
如果_________,
那么_______
a>b且c>0
ac>bc
不等式的性质2:不等式两边都乘(或除以)同一个____,不等号的方向____ 。
不等式的性质3:不等式两边都乘(或除以)同一个____,不等号的方向____。
如果 ________ ,那么 ______________
不变
正数
a>b,c>0
ac>bc (或 )
负数
改变
如果________,那么______________
a>b,c<0
ac
(1) 3a 3b;
(2) a-8 b-8;
(3) -2a -2b;
(4) 2a-5 2b-5;
(5) -3.5a-1 -3.5b-1.
>
>
<
<
>
不等式的性质2
不等式的性质1
不等式的性质3
不等式的性质1及2
不等式的性质1及3
练习: 已知a<0,用“<”或“>”号填空:
(1)a+2 ____2; (2)a-1 _____-1; (3)3a______ 0;
(4)-a/4______0; (5)a2_____0;
答:
(1)a+2<2,根据不等式的性质1.
(2)a-1<-1,根据不等式的性质1.
(3)3a<0,根据不等式的性质2.
(5)因为a<0,两边同乘a<0,
由不等式的性质3,得a2>0.
(4) -a/4>0,根据不等式的性质3.
将下列不等式化成x > a或 x < a 的形式,并说出根据.
(1) x- 7>26
(2) 3x < 2x +1
解:根据不等式的性质1 , 不等式两边都加上7,不等号方向不变,得, x >33
解:根据不等式的性质1,不等式两边都减去2x,不等号方向不变,得,x < 1
题目改为:利用不等式的性质解下列不等式, 并把解集在数轴上表示出来.
解:为了使不等式x- 7>26中不等号的一边变为x,根据不等式的性质1 , 不等式两边都加上7,不等号方向不变,得,
x- 7+7>26+7
x >33
这个不等式的解集在数轴上表示如下:
︱
0
○
33
锋 芒 初 试
利用不等式的性质解下列不等式,并在数轴上表示解集:
(1)3x<2x+1;
(2)x+5>-1;
(3)4x<3x-5.
我是最棒的
利用不等式的性质解下列不等式,并在数轴上表示解集:
(1) x>50;
(2) – 4x>3.
2
3
①在利用不等式的基本性质进行变形时,当不等式的两边都乘 (或除以)同一个字母,字母代表什么数是问题的关键,这决定了是用不等式的性质2还是性质3,也就是不等号是否要改变方向的问题;
②运用不等式的性质3时,要变两个号,一个是性质符号,另一个是不等号.
③ 补充两点:
(1)如果a>b,那么b<a 。
(2)如果a>b, b >c,那么 a > c。
